Loi normale
| Loi normale | |
 Densité de probabilité La courbe rouge représente la fonction , densité de probabilité de la loi normale centrée réduite. | |
 Fonction de répartition La courbe rouge représente la fonction , fonction de répartition de la loi normale centrée réduite. | |
| Paramètres | , espérance (nombre réel) , variance (nombre réel) |
|---|---|
| Support | |
| Densité de probabilité | |
| Fonction de répartition | |
| Espérance | |
| Médiane | |
| Mode | |
| Variance | |
| Asymétrie | 0 |
| Kurtosis normalisé | 0 |
| Entropie | |
| Fonction génératrice des moments | |
| Fonction caractéristique | |
| modifier |
|
En théorie des probabilités et en statistique, les lois normales sont parmi les lois de probabilité les plus utilisées pour modéliser des phénomènes naturels issus de plusieurs événements aléatoires. Elles sont en lien avec de nombreux objets mathématiques dont le mouvement brownien, le bruit blanc gaussien ou d'autres lois de probabilité. Elles sont également appelées lois gaussiennes, lois de Gauss ou lois de Laplace-Gauss des noms de Laplace (1749-1827) et Gauss (1777-1855), deux mathématiciens, astronomes et physiciens qui les ont étudiées.
Plus formellement, une loi normale est une loi de probabilité absolument continue qui dépend de deux paramètres : son espérance, un nombre réel noté μ, et son écart type, un nombre réel positif noté σ. La densité de probabilité de la loi normale d'espérance μ et d'écart type σ est donnée par :
La courbe de cette densité est appelée courbe de Gauss ou courbe en cloche, entre autres. C'est la représentation la plus connue de ces lois. Lorsqu'une variable aléatoire X suit une loi normale, elle est dite gaussienne ou normale et il est habituel d'utiliser la notation avec la variance σ2 :
La loi normale de moyenne nulle et d'écart type unitaire, , est appelée loi normale centrée réduite ou loi normale standard.
Parmi les lois de probabilité, les lois normales prennent une place particulière grâce au théorème central limite. En effet, elles correspondent au comportement, sous certaines conditions, d'une suite d'expériences aléatoires similaires et indépendantes lorsque le nombre d'expériences est très élevé. Grâce à cette propriété, une loi normale permet d'approcher d'autres lois et ainsi de modéliser de nombreuses études scientifiques comme des mesures d'erreurs ou des tests statistiques, en utilisant par exemple les tables de la loi normale centrée réduite.
Définition et explications informelles
[modifier | modifier le code]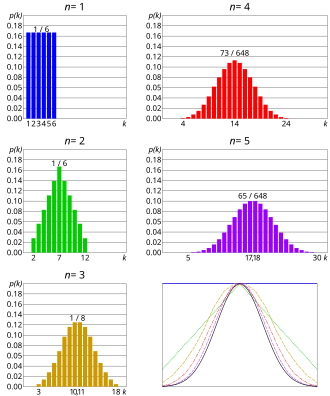
Les lois de probabilité permettent de décrire de manière théorique le caractère aléatoire d'une expérience qui est considérée comme aléatoire. Les lois normales en sont des cas particuliers. La manière historique de l'aborder est par approximation[1].
Lorsque le résultat de cette expérience aléatoire est à valeurs discrètes, par exemple la somme du lancer de deux dés vaut 2, 3… ou 12, une loi dite discrète modélise l'expérience. Les probabilités d'apparition de chaque valeur peuvent être représentées par des diagrammes en bâtons ou histogrammes (voir la figure ci-contre). Plusieurs scientifiques (voir Histoire de la loi normale) se sont intéressés à la réalisation d'un grand nombre d'expériences et au comportement de la loi de probabilité associée. Il apparaît que les fréquences d'apparition des valeurs possibles sont de plus en plus « lissées »[2] (voir la figure ci-contre). Il existe une certaine répartition autour d'une valeur centrale ; ces probabilités peuvent être alors représentées par une courbe de Gauss ou courbe en cloche obtenue par calcul ou par expérience[3]. Cette courbe est celle de la densité de probabilité d'une loi normale. Le rôle central de ces lois de probabilité vient du fait qu'elles sont la limite d'un grand nombre de lois de probabilité définies à partir de sommes, comme le montre le théorème central limite[4],[5].
Une autre manière visuelle de voir apparaître cette courbe est réalisée par la planche de Galton. Des billes sont lâchées en haut de la planche ; à chaque étage, elles ont deux possibilités : aller à droite ou aller à gauche. Après plusieurs étages, elles ont donc eu plusieurs choix aléatoires. Lorsque le nombre de billes est grand, la répartition des billes suivant leur position est approximativement une loi normale[6].
Comme pour toute loi de probabilité, plusieurs définitions équivalentes des lois normales existent : par leur densité de probabilité (la courbe de Gauss), par leur fonction de répartition, par leur fonction caractéristique, etc. Une loi normale dépend de deux paramètres : le premier donne la moyenne, c'est-à-dire la valeur « centrale » (ou « médiane ») des valeurs possibles[7] (par exemple, la moyenne de la somme de deux dés est 7) ; le deuxième paramètre renseigne sur la dispersion des valeurs autour de cette valeur centrale[7] : plus ce paramètre est faible, plus les valeurs proches de la valeur centrale auront une forte probabilité d'apparaître. Beaucoup de grandeurs physiques peuvent être représentées par ces deux paramètres[8].
Lors de l'étude statistique d'une série d'observations d'une même grandeur, la moyenne des valeurs observées peut être considérée comme une aléatoire suivant une loi normale. La moyenne de cette loi normale est alors considérée comme la valeur « réelle » de la grandeur observée, et la dispersion de la loi renseigne sur l'« erreur » d'observation[9]. C'est-à-dire qu'il est possible de calculer[9] une valeur approchée de la probabilité qu'une variable suivant une loi normale soit dans un intervalle [μ – σ, μ + σ] autour de la moyenne μ. Il s'agit de pouvoir obtenir une approximation de la grandeur observée dans l'expérience en considérant les erreurs dues aux instruments de mesure ou autres[2].
Histoire
[modifier | modifier le code]Une des premières apparitions d'une loi normale est due[a 1] à Abraham de Moivre en 1733 en approfondissant l'étude de la factorielle n! lors de l'étude d'un jeu de pile ou face. Il publie The Doctrine of Chances en 1756 dans lequel une loi normale apparaît comme limite d'une loi binomiale, ce qui sera à l'origine du théorème central limite[a 2]. En 1777, Pierre-Simon de Laplace reprend ces travaux et obtient une bonne approximation de l'erreur entre cette loi normale et une loi binomiale grâce à la fonction gamma d'Euler[a 1]. Dans son ouvrage publié en 1781[réf. souhaitée], Laplace donne une première table de cette loi. En 1809, Carl Friedrich Gauss assimile des erreurs d'observation en astronomie à la courbe, dite des erreurs, de la densité d'une loi normale[a 2].
Une loi normale est alors pleinement définie lorsque le premier théorème central limite, alors appelé théorème de Laplace, est énoncé par Laplace en 1812[a 1]. Son nom « normale » est donné par Henri Poincaré à la fin du XIXe siècle[10]. Les lois normales portent également les noms de lois de Gauss ou lois de Laplace-Gauss[11] en fonction de l'attribution de la paternité de la création de ces lois ; la dénomination de deuxième loi de Laplace est également utilisée occasionnellement[12].
Les études sur les lois normales se poursuivent durant le XIXe siècle. Ainsi, de nouvelles tables numériques sont données en 1948 par Egon Sharpe Pearson, en 1952 par le National Bureau of Standards[13] et en 1958 par Greenwood et Hartley[14].
Loi normale centrée réduite
[modifier | modifier le code]Une loi normale est une loi de probabilité (c'est-à-dire une mesure N de masse totale unitaire[a 3]) unidimensionnelle (c'est-à-dire à support réel ). C'est une loi absolument continue, c'est-à-dire que la mesure est absolument continue par rapport à la mesure de Lebesgue. Autrement dit, il existe une densité de probabilité, souvent notée φ pour la loi normale centrée réduite, telle que : N(dx) = φ(x) dx. Elle est généralisée par la loi normale multidimensionnelle. La loi normale centrée réduite est appelée loi normale standard[15].
Définition par la fonction de densité
[modifier | modifier le code]
La loi normale centrée réduite est la loi de probabilité absolument continue dont la densité de probabilité est donnée par la fonction définie par[16] : , pour tout . Cette loi est dite centrée puisque son moment d'ordre 1 (espérance) vaut 0 et réduite puisque son moment d'ordre 2 (variance) vaut 1, tout comme son écart type. Le graphe de la densité φ est appelé fonction gaussienne, courbe de Gauss ou courbe en cloche. Cette loi est notée grâce à la première lettre de « normal », une variable aléatoire X qui suit la loi normale centrée réduite est notée : .
Quelques remarques et propriétés immédiates (voir également les propriétés ci-dessous) :
- le calcul de l'intégrale de Gauss permet de démontrer que la fonction φ est une densité de probabilité par la formule : ;
- la densité φ est continue, uniformément bornée et paire[17] ;
- cette parité fait que l'espérance et les moments d'ordres impairs sont nuls ;
- les moments d'ordres pairs sont donnés par [18](en particulier, Var(X) = m2 = 1), d'après la relation de récurrence m2k = (2k–1)m2k–2 pour k ≥ 1, qui provient de l'intégration par parties suivante :.
- le maximum de la fonction φ est atteint en la moyenne 0 et vaut[17] ;
- la fonction vérifie : ;
- la densité φ est infiniment dérivable ; un raisonnement par récurrence permet d'obtenir la formule[19] : où Hn est le n-ième polynôme d'Hermite ;
- la densité possède[a 3] deux points d'inflexion en 1 et en –1. Ce sont les points en lesquels la dérivée seconde φ'' s'annule et change de signe. Les deux points se situent approximativement aux trois cinquièmes de la hauteur totale.
Définition par la fonction de répartition
[modifier | modifier le code]
Historiquement, une loi normale est apparue comme la loi limite dans le théorème central limite à l'aide de sa fonction de répartition. Il est alors utile de définir la loi par cette fonction. La loi normale est la loi de probabilité dont la fonction de répartition est donnée par la fonction définie par[18] : , pour tout . Elle donne la probabilité qu'une variable aléatoire de loi normale appartienne à un intervalle : (pour plus de détails de calcul, voir la section Tables numériques et calculs).
Quelques remarques et propriétés immédiates :
- il n'existe pas d'expression analytique de la fonction de répartition Φ, c'est-à-dire qu'elle ne s'exprime pas à partir de fonctions usuelles mais devient elle-même une fonction usuelle[20] ;
- elle s'exprime en fonction de la fonction d'erreur grâce aux deux formules équivalentes suivantes[a 4] :
- ,
- ;
- elle est dérivable une infinité de fois et vérifie Φ'(x) = φ(x). L'écriture équivalente dΦ(x) = φ(x)dx permet de définir l'intégrale de Lebesgue-Stieltjes par rapport à la loi normale ;
- elle est absolument continue et strictement croissante, c'est donc une bijection[a 5] de dans ]0 ; 1[. Sa réciproque Φ−1 existe et s'appelle la fonction probit. Cette fonction est utilisée pour le modèle probit[21] ;
- par parité de la loi, Φ(–x) = 1 – Φ(x) et ainsi Φ(0) = 12. Ceci montre[a 5] que la médiane de la loi normale centrée réduite est 0 ;
- par définition de la fonction de répartition, lorsque la variable aléatoire X suit la loi normale centrée réduite, . Pour obtenir les valeurs de cette probabilité, il faut approcher cette fonction par d'autres fonctions usuelles et il existe des tables de valeurs (voir la section Table de la loi normale ci-dessous).
Définition par la fonction caractéristique
[modifier | modifier le code]
La caractérisation d'une loi normale par sa fonction caractéristique présente un intérêt pour démontrer certaines propriétés, comme la stabilité par addition ou le théorème central limite. Cette fonction caractéristique , qui se calcule à partir de la densité de probabilité[18],[22] et caractérise la loi, est donnée par : . Cette fonction caractéristique est égale, à une constante multiplicative près, à la densité de probabilité de la loi : on dit que la fonction caractéristique d'une gaussienne est gaussienne[a 3].
Si une variable aléatoire X suit la loi normale centrée réduite de fonction caractéristique ϕ définie ci-dessus, alors[23] la transformation linéaire Y = aX+b admet pour fonction caractéristique : . C'est donc une variable aléatoire de loi normale de moyenne b et de variance a2.
Définition par la fonction génératrice des moments
[modifier | modifier le code]Une autre manière de définir une loi normale est par l'utilisation de sa fonction génératrice des moments . Cette fonction, qui se calcule à partir de la fonction de densité[b 1] et caractérise la loi, est donnée par[24] : , pour tout . On retrouve ainsi les valeurs des moments mn (voir supra).
Loi normale générale
[modifier | modifier le code]Définition
[modifier | modifier le code]Plus généralement que la loi normale centrée réduite, une loi normale (non centrée et non réduite) est une loi de probabilité absolument continue dont l'un des quatre points suivants est vérifié :
- la densité de probabilité est donnée par[16] :, pour tout ;
- la fonction de répartition est donnée par :, pour tout ;
- la fonction caractéristique est donnée par[25] :, pour tout ;
- la fonction génératrice des moments est donnée par[26],[27],[b 2] :, pour tout ,où et .
Pour le cas où σ = 0, c'est une forme dégénérée de la loi normale, parfois appelée loi normale impropre[25]. C'est alors la mesure de Dirac au point μ qui n'est pas absolument continue.
La valeur μ est la moyenne de la loi et σ est l'écart type alors que σ2 en est la variance. Cette loi est notée grâce à la première lettre de « normal ». Une variable aléatoire X qui suit une loi normale est notée de deux manières différentes suivant les auteurs[28],[15] : La deuxième notation a l'intérêt de pouvoir noter la stabilité par addition de manière simple[a 5] ; elle sera utilisée dans cet article.
Remarques et propriétés immédiates
[modifier | modifier le code]- Si la variable aléatoire X suit la loi normale centrée réduite , alors la variable aléatoire σX + μ suit la loi normale de moyenne μ et de variance σ2. Réciproquement, si Y suit la loi normale , alors Y – μσ suit la loi normale centrée réduite[1]. Dit autrement, toute loi normale peut s'obtenir par translation (shifting en anglais) et par dilatation (scaling en anglais) de la loi centrée réduite.Cette première propriété permet d'obtenir la formule très utile[29] :.Il est alors possible de déduire les propriétés d'une loi normale à partir de celles de la loi normale centrée réduite, et vice versa. La variable Y – μσ est parfois[30] appelée la « standardisation » de Y ou « variable Y centrée réduite ».
- Plus généralement, si alors (on peut le lire sur les fonctions génératrices des moments[31], ou sur les densités).
- La densité f est symétrique par rapport à μ[17].
- Le maximum de la fonction f est atteint en μ et vaut[17] .
- La décroissance de la densité à droite et à gauche de μ est surexponentielle[17].
- Puisqu'une loi normale est une loi de probabilité absolument continue, l'événement [X = x] est négligeable, c'est-à-dire que presque sûrement une variable aléatoire de loi normale X n'est jamais égale à une valeur fixée x. Ceci se traduit mathématiquement par : .
- La largeur à mi-hauteur permet de donner une valeur d'amplitude de la loi. C'est la largeur de la courbe à une hauteur qui vaut la moitié de la hauteur totale. Cette largeur à mi-hauteur de la loi normale est proportionnelle à l'écart type[a 6] : H = 2 √2 ln (2) σ ≈ 2,3548 σ. Le facteur 2 est issu de la propriété de symétrie de la loi normale.
- La densité possède[a 3] deux points d'inflexion en μ + σ et en μ – σ. Ce sont les points en lesquels la dérivée seconde f'' s'annule et change de signe. Les deux points se situent approximativement aux trois cinquièmes de la hauteur totale.
- Les lois normales sont des lois de la famille exponentielle, c'est-à-dire que leur densité s'écrit sous la forme : ou, de manière équivalente, sous la forme[32].
Propriétés
[modifier | modifier le code]Autres caractérisations
[modifier | modifier le code]En addition de la densité de probabilité, de la fonction de répartition, de la fonction caractéristique et de la fonction génératrice des moments, il existe d'autres caractérisations des lois normales.
- Caractérisation due à Georges Darmois (1951) et Sergueï Bernstein (1954)[a 2] : si deux variables aléatoires X1 et X2 sont indépendantes et de même loi et si les deux variables aléatoires X1 + X2 et X1 – X2 sont également indépendantes, alors la loi commune X1 et X2 est une loi normale.
- Caractérisation due à Charles Stein (1972)[a 3] : les lois normales sont les seules lois de probabilité (mesures de probabilité) telles que, pour toute fonction g de classe C¹ (c'est-à-dire dérivable et de dérivée continue) :.
Moments
[modifier | modifier le code]Le moment d'ordre 1 est appelé la moyenne (μ) et est donné en paramètre d'une loi normale . Le deuxième paramètre est son écart type (σ), c'est-à-dire la racine carrée de la variance qui est par définition la moyenne des carrés des écarts à la moyenne. Il est alors également intéressant d'obtenir les moments centrés d'une loi normale, ils sont donnés par[31] :
pour et X une variable aléatoire de loi normale .
Le moment ordinaire mn peut s'obtenir à partir des moments d'ordre inférieur à n – 1 et du moment centré d'ordre n, en utilisant la formule qui exprime μn en fonction de m0, m1, ..., mn. Les premiers moments d'une loi normale sont alors[33] : .
Calcul direct
[modifier | modifier le code]Grâce à la symétrie autour de μ de la fonction de densité d'une loi normale, les moments centrés d'ordre impair sont tous nuls[31].
Des moments d'ordre pairs de la loi normale centrée réduite (voir supra), on déduit la formule des moments centrés : .
Par la fonction génératrice des moments
[modifier | modifier le code]Les moments centrés (μn, n ≥ 0) d'une loi peuvent s'obtenir à partir de la fonction génératrice des moments centrés. Le cas particulier μ = 0 de la fonction génératrice des moments (voir supra) donne : .
Comme par ailleurs on a (pour toute loi) , on en déduit, par identification des coefficients des deux séries[31], les moments centrés d'une loi normale (voir supra).
Quant aux moments ordinaires, leur fonction génératrice permet d'établir la relation de récurrence[b 3] :
- .
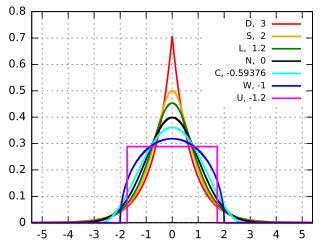
Asymétrie et aplatissement
[modifier | modifier le code]L'asymétrie γ1, le kurtosis β2 et le kurtosis normalisé γ2 s'obtiennent à partir des formules des moments[34] :
;
;
.
Les lois normales servent de point de référence pour la comparaison des épaisseurs de traîne : si une loi possède un kurtosis normalisé γ2 > 0, alors la loi possède une traîne plus épaisse qu'une loi normale et est dite leptokurtique ; à l'inverse si γ2 < 0, la loi possède une traîne moins épaisse qu'une loi normale et est appelée platikurtique ; les lois de kurtosis normalisé nul possèdent une traîne comparable à la loi normale et sont dites mésokurtiques.
Cumulants
[modifier | modifier le code]La fonction caractéristique permet d'obtenir la fonction génératrice des cumulants par la formule et permet d'obtenir les cumulants[35] : K1 = μ, K2 = σ2 et Kn = 0 pour n ≥ 3.
Théorèmes de convergence
[modifier | modifier le code]
La première version du théorème central limite, appelé alors théorème de Moivre-Laplace, a été énoncée dans le cas de variables aléatoires de loi de Bernoulli. De manière plus générale, si X1, X2, ..., Xn sont des variables indépendantes et identiquement distribuées de variance finie et si la somme est notée Sn = X1 + X2 + ... + Xn, alors[20] pour tout a < b où φ est la densité de probabilité de la loi normale centrée réduite.
Ce théorème signifie que tout ce qui peut être considéré comme étant la somme d'une grande quantité de petites valeurs aléatoires indépendantes et identiquement distribuées est approximativement de loi normale[36]. Ceci montre le caractère central des lois normales en théorie des probabilités. Un énoncé physique de ce théorème peut être formulé[37] : Si une grandeur physique subit l'influence additive d'un nombre important de facteurs indépendants et si l'influence de chaque facteur pris séparément est petite, alors la distribution de cette grandeur est une distribution gaussienne.
Ce théorème central limite est valide pour toute loi de probabilité initiale des variables iid X1, X2, ..., Xn ayant un écart type fini, il permet d'obtenir de bonnes approximations de la somme Sn, par exemple[38] :
- si les variables Xi sont de loi de Bernoulli , alors Sn suit approximativement une loi normale . Cette approximation est satisfaisante[39] dans le cas où np(1–p) > 10 ;
- si les variables Xi sont de loi du χ² : χ2(1), alors Sn suit approximativement une loi normale ;
- si les variables Xi sont de loi exponentielle : , alors Sn suit approximativement une loi normale .
Il existe des versions plus générales de ce théorème, par exemple en considérant des variables aléatoires indépendantes, pas de même loi mais ayant des variances petites comparées à celle de leur moyenne[40]. Un théorème de Gnedenko et Kolmogorov (1954) stipule qu'une variable aléatoire normale est la somme d'un grand nombre de variables aléatoires indépendantes petites dont aucune n'est prépondérante :
Théorème — Considérons une suite de variables aléatoires (Xn, n ≥ 1) dont chacune est la somme d'un nombre fini de variables aléatoires avec .
Pour tout ε > 0, introduisons la variable aléatoire tronquée :
et supposons :
- (en probabilité) ;
- pour tout ε > 0, et .
Alors la loi de Xn converge vers la loi normale .
Stabilités et famille normale
[modifier | modifier le code]Stabilité par additivité (propriété de conservation)
[modifier | modifier le code]Les lois normales sont stables par additivité[a 2], c'est-à-dire que la somme de deux variables aléatoires indépendantes de lois normales est elle-même une variable aléatoire de loi normale. Plus explicitement : si , et X1 et X2 sont indépendantes, alors la variable aléatoire suit la loi normale .
Cette propriété se généralise pour n variables, c'est-à-dire que si pour tout , les variables aléatoires Xi suivent une loi normale et sont indépendantes, alors[41] la somme X1 + X2 + ... + Xn suit une loi normale .
Cette propriété se démontre directement au moyen des fonctions caractéristiques. La densité de probabilité de la somme de deux variables indépendantes de loi normale est donnée par la convolution des deux densités. Ceci se traduit par les formules de convolution de fonctions[25] ou de convolution de mesures normales[42] que l'on note : et .
Il ne faut pas confondre avec la loi dont la densité est la somme de densités de lois normales (voir la section Constructions à partir de la loi normale ci-dessous).

Famille normale
[modifier | modifier le code]L'ensemble de fonctions forme la famille dite famille normale. La famille normale est également le nom de l'ensemble des lois normales[42] . La famille de fonctions est fermée pour la convolution au sens où[43] : la fonction φ est la seule qui engendre la famille ; si la convolution de deux densités est dans la famille alors les deux fonctions sont dans la famille ; et toute densité convolée un nombre suffisamment grand de fois et convenablement renormalisée est proche d'une fonction de la famille normale. Les trois théorèmes suivants donnent plus de précisions mathématiques.
- Théorème[43] : si pour une fonction de densité f de moyenne 0 et d'écart type 1, il existe et satisfaisant :,alors est la densité de la loi normale centrée réduite.
- Théorème de Lévy-Cramér (1936) (conjecturé par Paul Lévy en 1935)[44],[a 2] : si deux fonctions de densité, f1 et f2, vérifient :,alors et avec μ1 + μ2 = μ et σ1 + σ2 = σ. Autrement dit, si la somme de deux variables aléatoires indépendantes est normale, alors les deux variables sont de lois normales.
- Théorème[44] : si f est la densité commune de n variables aléatoires indépendantes de moyenne 0 et d'écart type 1, alors la convolée n fois de f converge uniformément en x : (ce théorème est équivalent au théorème central limite). Il ne faut pas confondre cette famille normale avec la famille normale de fonctions holomorphes.
Stabilité par linéarité
[modifier | modifier le code]Les lois normales sont stables par linéarité : si α ≥ 0 et β sont deux réels et , alors[45] la variable aléatoire αX + β suit la loi normale .
Grâce aux stabilités par addition et par linéarité, une loi normale est un cas particulier de loi stable[a 7] avec pour paramètre de stabilité α = 2. Parmi les lois stables, les lois normales, la loi de Lévy (α = 1/2) et la loi de Cauchy (α = 1) sont les seules à posséder une expression analytique de leur fonction de densité.
Stabilité par moyenne
[modifier | modifier le code]Les lois normales sont stables par moyennisation, c'est-à-dire si X1, X2, ..., Xn sont des variables aléatoires indépendantes suivant respectivement les lois normales , alors la moyenne 1n(X1 + X2 + ... + Xn) suit la loi .
Convexité
[modifier | modifier le code]Les lois normales ne sont pas convexe[46], c'est-à-dire que l'inégalité pour tous boréliens A et B n'est pas vérifiée lorsque la mesure est normale. Cependant, lorsque l'on normalise cette inégalité avec l'inverse de la fonction de répartition de la loi normale centrée réduite, on obtient le théorème suivant, analogue à l'inégalité de Brunn-Minkowski-Lusternik pour la mesure de Lebesgue dans :
Inégalité de Ehrhard — Pour la mesure normale standard , pour tous ensembles boréliens A et B et pour tout λ ∈ ]0 ; 1[,
En fait, les lois normales font partie de la famille des distributions de mesures log-concaves, c'est-à-dire vérifiant pour tous boréliens A et B et tout ,
Entropie et quantité d'information
[modifier | modifier le code]Entropie de Shannon
[modifier | modifier le code]L'entropie de Shannon d'une loi de probabilité absolument continue de densité donnée par f permet de mesurer une quantité d'information et est définie par : . Dans l'ensemble des lois absolument continues de variance σ2 fixée, les lois normales sont d'entropie maximum[a 8]. L'entropie maximum, pour une loi normale donc, est donnée par : H = ln (σ √2πe). Ainsi la théorie de maximisation de l'entropie dit que, même si elle n'est pas la meilleure loi adaptée aux valeurs, une loi normale ajustée aux valeurs est adéquate pour prendre une décision.
Il y a également une connexion entre la convergence de suites de lois de probabilité vers une loi normale et la croissance de l'entropie, ce qui en fait un outil majeur dans la théorie de l'information[a 2].
La quantité d'information de Fisher
[modifier | modifier le code]L'information de Fisher d'une loi à densité de probabilité est une autre notion de quantité d'information. Pour une densité f, elle est donnée par : . Pour toute densité suffisamment régulière d'une loi centrée réduite, cette information vérifie I ≥ 1. Les lois normales se distinguent des autres densités puisque l'inégalité précédente est une égalité si et seulement si la densité est celle de la loi normale centrée réduite[a 2].
Distance entre lois
[modifier | modifier le code]La divergence de Kullback-Leibler entre deux lois permet de mesurer une distance entre les deux lois, ou une perte d'information entre les deux lois. La divergence de Kullback-Leibler entre les deux lois normales et est : . Cette divergence est nulle pour μ1 = μ2 et σ1 = σ2 ; de plus, elle croît lorsque croît[a 9].
Approximation de la fonction de répartition
[modifier | modifier le code]Il n'existe pas d'expression analytique pour la fonction de répartition Φ de la loi normale centrée réduite, c'est-à-dire qu'il n'existe pas de formule simple entre la fonction de répartition et les fonctions classiques telles que les fonctions polynomiales, exponentielle, logarithmique, trigonométriques, etc. Cependant la fonction de répartition apparaît dans plusieurs résultats à vocation à être appliqués, il est donc important de mieux cerner cette fonction. Différentes écritures sous forme de séries ou de fractions continues généralisées sont possibles[47].
Pour les valeurs de , la fonction de répartition de la loi normale centrée réduite s'écrit sous la forme[a 10] : , ou sous la forme : .
Pour , la fonction de répartition de la loi normale centrée réduite s'écrit sous la forme[47],[a 10] : avec .
De manière plus numérique et facilement calculable, les approximations suivantes donnent des valeurs de la fonction de répartition Φ de la loi normale centrée réduite avec :
- une erreur de l'ordre de[48] 10−5 : pour x > 0, où ;
- une erreur de l'ordre de[48] : pour : ;
- une erreur de l'ordre de[a 10] :
Voici un exemple d'algorithme[a 4] pour le langage C :
double Phi(double x){
long double s=x,t=0,b=x,q=x*x,i=1;
while(s!=t)
s = (t=s) + (b*=q/(i+=2));
return 0.5 + s*exp(-0.5*q - 0.91893853320467274178L);
}
Une autre écriture de la fonction de répartition de la loi normale centrée réduite utilise une fraction continue généralisée[a 4] : .
Tables numériques et calculs
[modifier | modifier le code]
Comme mentionné dans la section précédente, il est utile de bien connaître la fonction de répartition Φ pour les applications numériques. Des tables de valeurs ont alors été calculées pour la fonction de répartition, mais également pour son inverse, ce qui permet d'obtenir les quantiles et les intervalles de confiance pour un seuil de tolérance fixé.[réf. nécessaire]
La table suivante donne les valeurs de la fonction de répartition , lorsque X suit la loi normale centrée réduite .
Les valeurs en début de lignes donnent la première partie de la variable, les valeurs en début de colonnes donnent la deuxième partie. Ainsi la case de la deuxième ligne et troisième colonne donne : Φ(0,12) = 0,54776.

| 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,0 | 0,50000 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,52790 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,54380 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 0,61026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,62930 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,65910 | 0,66276 | 0,66640 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,70540 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,72240 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,75490 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,76730 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,78230 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1,0 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,86650 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,87900 | 0,88100 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,90320 | 0,90490 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,92220 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,94520 | 0,94630 | 0,94738 | 0,94845 | 0,94950 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,96080 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,97320 | 0,97381 | 0,97441 | 0,97500 | 0,97558 | 0,97615 | 0,97670 |
| 2,0 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,98030 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,98300 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,98500 | 0,98537 | 0,98574 |
| 2,2 | 0,98610 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,98840 | 0,98870 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,99010 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,99180 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,99430 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,99520 |
| 2,6 | 0,99534 | 0,99547 | 0,99560 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,99720 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,99760 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3,0 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,99900 |
| 3,1 | 0,99903 | 0,99906 | 0,99910 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,99940 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,99950 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,99960 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,99970 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,99980 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,99990 | 0,99990 | 0,99990 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
Les deux tables suivantes donnent[49] les valeurs du quantile de la loi normale centrée réduite défini par .
Les valeurs en début de ligne donne la première partie de la variable, les valeurs en début de colonne donne la deuxième partie. Ainsi la case de la deuxième ligne et troisième colonne donne : .
| 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,50 | 0,0000 | 0,0251 | 0,0502 | 0,0753 | 0,1004 | 0,1257 | 0,1510 | 0,1764 | 0,2019 | 0,2275 |
| 0,60 | 0,2533 | 0,2793 | 0,3055 | 0,3319 | 0,3585 | 0,3853 | 0,4125 | 0,4399 | 0,4677 | 0,4959 |
| 0,70 | 0,5244 | 0,5534 | 0,5828 | 0,6128 | 0,6433 | 0,6745 | 0,7063 | 0,7388 | 0,7722 | 0,8064 |
| 0,80 | 0,8416 | 0,8779 | 0,9154 | 0,9542 | 0,9945 | 1,036 | 1,080 | 1,126 | 1,175 | 1,227 |
| 0,90 | 1,282 | 1,341 | 1,405 | 1,476 | 1,555 | 1,645 | 1,751 | 1,881 | 2,054 | 2,326 |
Cette table donne les valeurs des quantiles pour p grand.
| p | 0,975 | 0,995 | 0,999 | 0,9995 | 0,9999 | 0,99995 | 0,99999 | 0,999995 |
|---|---|---|---|---|---|---|---|---|
| 1,9600 | 2,5758 | 3,0902 | 3,2905 | 3,7190 | 3,8906 | 4,2649 | 4,4172 |
Les tables sont données pour les valeurs positives de la loi normale centrée réduite. Grâce aux formules de la fonction de répartition, il est possible d'obtenir d'autres valeurs.
Les valeurs négatives de la fonction de répartition sont données par la formule[14] Φ(–x) = 1 – Φ(x). Par exemple : pour .
Les valeurs de la fonction de répartition de la loi générale s'obtiennent par la formule[50] . Par exemple[51] : , pour .
La table de valeurs permet également d'obtenir la probabilité qu'une variable aléatoire de loi normale appartienne à un intervalle donné [a , b] par la formule : . Par exemple :
- pour ;
- pour .
Plages de normalité, intervalles de confiance
[modifier | modifier le code]Un des intérêts de calculer des probabilités sur des intervalles est l'utilisation des intervalles de confiance pour les tests statistiques. Une loi normale est définie par deux valeurs : sa moyenne μ et son écart type σ. Ainsi il est utile de s'intéresser aux intervalles[52] du type [μ – rσ, μ + rσ]. pour .

La table suivante s'obtient grâce aux tables précédentes[52] et donne les probabilités : .
| r | 0,0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,3829 | 0,6827 | 0,8664 | 0,9545 | 0,9876 | 0,9973 | 0,9995 |
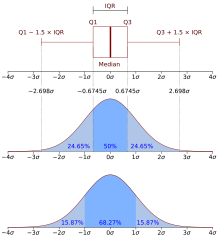
Cette table de valeurs des intervalles de confiance permet d'obtenir les plages de normalité pour un niveau de confiance donné. Pour , le tableau donne[9] :
- .L'intervalle [μ – σ, μ + σ] est la plage de normalité au niveau de confiance 68 % ;
- .L'intervalle [μ – 0,5H, μ + 0,5H], H étant la largeur à mi-hauteur, est la plage de normalité au niveau de confiance 76 % ;
L'intervalle [μ – 2σ, μ + 2σ] est la plage de normalité au niveau de confiance 95.4 % ;
L'intervalle [μ – 1.96σ, μ + 1.96σ] est la plage de normalité au niveau de confiance 95 % (voir 97,5ème centile)
- L'intervalle [μ – 3σ, μ + 3σ] est la plage de normalité au niveau de confiance 99 %.
Inversement, lorsque la valeur de la probabilité α ∈ [0 ; 1] est fixée, il existe[a 5] une unique valeur telle que : . L'intervalle [μ – rσ, μ + rσ] est appelé plage de normalité ou intervalle de confiance au niveau de confiance α. Pour une loi normale et le seuil α donnés, la méthode pour retrouver cette valeur r consiste[53] à utiliser le tableau de valeur des quantiles (ci-dessus) pour trouver la valeur r telle que Φ(r) = α + 12 ; l'intervalle de confiance est alors [μ – rσ, μ + rσ].
Par exemple, la plage de normalité au niveau de confiance 95 % d'une loi normale est l'intervalle [10 – 2r, 10 + 2r] où r vérifie Φ(r) = 0,95 + 12 = 0,975, soit r = q0,975 ≈ 1,96, l'intervalle est donc : [6,08 ; 13,92] aux arrondis près.
Liens avec d'autres lois
[modifier | modifier le code]Grâce à son rôle central parmi les lois de probabilité et dans les applications, les lois normales possèdent beaucoup de liens avec les autres lois. Certaines lois sont même construites à partir d'une loi normale pour mieux correspondre aux applications.
Lois usuelles
[modifier | modifier le code]| Lois | en fonction de variables de loi normale |
|---|---|
| loi du χ² | |
| loi du χ² non centrée | |
| loi du χ | |
| loi du χ non centrée |
Lois unidimensionnelles
[modifier | modifier le code]- Si une variable aléatoire suit la loi normale , alors[54] la variable aléatoire suit la loi log-normale.
- Si U et V sont deux variables aléatoires indépendantes de loi uniforme sur [0, 1], alors les deux variables aléatoires et sont de loi normale centrée réduite[50]. De plus X et Y sont indépendantes. Ces deux formules sont utilisées pour simuler la loi normale.
- Si les variables sont indépendantes et de loi commune , alors[55] la somme de leur carré : suit une loi du χ² à n degrés de liberté : . La formule s'étend pour des variables normales non centrées et non réduites. De plus, le même type de lien existe avec la loi du χ² non centrée, la loi du χ et la loi du χ non centrée (voir le tableau ci-contre).
- Si la variable U suit la loi normale centrée réduite : , si V suit une loi du χ2 à n degrés de liberté et si U et V sont indépendantes, alors[55] la variable suit une loi de Student à n degrés de liberté : .
- Si est une variable aléatoire de loi normale centrée réduite et de loi uniforme sur [0, 1], alors est de loi dite de Slash[a 11].
- Pour une variable aléatoire de loi normale centrée réduite , la variable est de loi normale puissance p. Pour , cette variable est de loi normale centrée réduite[a 11].
- Si et sont deux variables aléatoires indépendantes de loi normale centrée réduite, alors[56] le quotient suit la loi de Cauchy de paramètre 0 et 1 : . Dans le cas où et sont deux gaussiennes quelconques (non centrées, non réduites), le quotient suit une loi complexe dont la densité s'exprime en fonction de polynômes d'Hermite (l'expression exacte est donnée par Pham-Gia en 2006[a 12]).
Lois multidimensionnelles
[modifier | modifier le code]- Il existe une version multidimensionnelle d'une loi normale, appelée loi normale multidimensionnelle, loi multinormale ou loi de Gauss à plusieurs variables. Lorsque sont des variables aléatoires de lois normales, alors la loi de probabilité du vecteur aléatoire est de loi normale multidimensionnelle. Sa densité de probabilité prend la même forme que la densité d'une loi normale mais avec une écriture matricielle. Si le vecteur aléatoire est de loi normale multidimensionnelle où μ est le vecteur des moyennes et est la matrice de variance-covariance, alors la loi conditionnelle de sachant que est la loi normale[57] :Si , alors avec et .
- La loi de la norme euclidienne d'un vecteur dont les coordonnées sont indépendantes et de lois normales centrées, de même variance, est une loi de Rayleigh[a 2].
Il est à noter que la loi inverse-gaussienne et loi inverse-gaussienne généralisée n'ont pas de lien avec une formule simple créée à partir de variables de loi normale, mais ont une relation avec le mouvement brownien.
Lois normales généralisées
[modifier | modifier le code]Plusieurs généralisations de la loi normale ont été introduites afin de changer sa forme, son asymétrie, son support, etc.
Un nouveau paramètre dit de forme peut être introduit dans une loi normale pour obtenir une loi normale généralisée. Cette famille de lois contient les lois normales, c'est le cas pour , mais également la loi de Laplace pour . La nouvelle densité de probabilité est donnée par[a 13] .
Il existe une manière de changer l'asymétrie d'une loi normale afin d'obtenir une loi dite loi normale asymétrique (skew normal distribution en anglais)[a 14]. L'introduction d'un paramètre permet d'obtenir une loi normale lorsque , une asymétrie vers la droite lorsque et une asymétrie vers la gauche lorsque . La densité de cette loi est donnée par : .
Afin de changer le support d'une loi normale et notamment de le rendre borné, une modification possible de cette loi est de la tronquer. Elle est alors changée d'échelle pour que les parties coupées se répartissent sur l'ensemble des valeurs gardées (à la différence de la loi repliée, voir ci-dessous). La loi normale centrée réduite tronquée en –T et en T a pour support l'intervalle et sa fonction de densité se définit par[a 15] :
Il est également possible de tronquer une loi normale d'un seul côté. Elle est alors appelée « loi normale rectifiée ». Si une variable aléatoire suit la loi normale , alors suit la loi normale rectifiée[a 16].
Une autre manière de changer le support de la loi normale est de « replier » la densité à partir d'une valeur, la loi obtenue est une loi normale repliée. Les valeurs retirées, par exemple , sont alors réparties proche de la valeur charnière, 0 ici (à la différence de la loi tronquée, voir ci-dessus). La densité de probabilité de la loi normale repliée en 0 est donnée par[a 17] :
Une version généralisée de la loi log-normale permet d'obtenir une famille de lois comprenant les lois normales comme cas particulier[58]. La famille est définie à partir de trois paramètres : un paramètre de position μ, un paramètre d'échelle σ et un paramètre de forme . Lorsque , cette loi log-normale généralisée est la loi normale. La densité est donnée par : , où
 |
 |
 |
 |
 |
Constructions à partir d'une loi normale
[modifier | modifier le code]Mélange de lois
[modifier | modifier le code]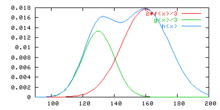
Un mélange gaussien est une loi de probabilité dont la densité est définie par une combinaison linéaire de deux densités de lois normales. Si l'on note la densité de et la densité de , alors est la densité d'une loi de probabilité dite mélange gaussien[59].
Il ne faut pas confondre la combinaison linéaire de deux variables aléatoires indépendantes de loi normale, qui reste une variable gaussienne, et la combinaison linéaire de leurs deux densités, qui permet d'obtenir une loi qui n'est pas une loi normale.
Les modes des deux lois normales sont donnés par μ1 et μ2, le mélange gaussien est alors une loi bimodale. Ses maxima locaux sont proches de mais non égaux[59] aux valeurs μ1 et μ2.
Généralités
[modifier | modifier le code]Il est possible de construire d'autres densités de probabilité grâce à la densité de la loi normale centrée réduite. Harald Cramér énonce en 1926 un résultat général[60] : si une densité de probabilité est deux fois dérivable, si l'intégrale converge et si , alors la fonction peut être développée en une série absolument et uniformément convergente en fonction des dérivées de la densité de la loi normale centrée réduite et des polynômes d'Hermite : .
Utilisations
[modifier | modifier le code]Historiquement, les lois normales sont introduites lors d'études d'objets célestes ou de jeux de hasard. Elles sont ensuite étudiées et généralisée mathématiquement puis elles sont utilisées dans de nombreuses autres applications : en mathématiques, dans d'autres sciences exactes, dans des sciences plus appliquées ou des sciences humaines et sociales. Voici une sélection d'exemples.
Balistique
[modifier | modifier le code]Au XIXe siècle, pour améliorer les précisions des tirs de l'artillerie, de nombreux tirs de canons sont réalisés. Il est observé que la direction et la portée sont assimilables à des lois normales[a 18]. Cette compréhension permet de mieux entraîner les servants pour régler les tirs. Ces lois normales proviennent de différents facteurs comme les conditions climatiques, mais également de l'usure du matériel militaire. La dispersion des points d'impact, et donc de la loi, renseigne sur l'état du matériel et sur le nombre éventuel de tirs anormaux. L'ajustement à une loi normale est alors effectué par le test de Lhoste sur une série de 200 tirs. Le mathématicien Jules Haag applique la méthode pour 2 680 tirs de différentes portées et de différentes directions[a 18].
Quotient intellectuel
[modifier | modifier le code]Le quotient intellectuel (QI) a pour objectif de donner une valeur numérique à l'intelligence humaine. En 1939, David Wechsler donne une définition à ce quotient de manière statistique. Une note de 100 est donnée à la moyenne des valeurs obtenues dans une population de même âge et 15 points sont retranchés pour un écart égal à l'écart type obtenu à partir des valeurs de la population testée[61]. Pour cette raison, en pratique, la courbe de répartition du QI est modélisée par la courbe en cloche de la loi normale centrée en 100 et d'écart type 15 : . Cependant cette modélisation est remise en cause par certains scientifiques. En effet, les résultats des tests dépendraient des classes sociales ; la population ne serait donc plus homogène, c'est-à-dire que la propriété d'indépendance des individus ne serait pas vérifiée[a 19]. Le quotient intellectuel ne serait alors qu'une approximation de mesure de l'intelligence humaine dont on ne connaît pas l'erreur.[réf. nécessaire]
Anatomie humaine
[modifier | modifier le code]
Un caractère observable et mesurable dans une population d'individus comparables a souvent une fréquence modélisée par une loi normale. C'est le cas par exemple de la taille humaine pour un âge donné (en séparant les hommes et les femmes)[62], de la taille des becs dans une population d'oiseaux comme les pinsons de Darwin étudiés par Darwin[63]. Plus précisément, un caractère mesurable dans une population peut être modélisé à l'aide d'une loi normale s'il est codé génétiquement par de nombreux allèles ou par de nombreux loci[63] ou si le caractère dépend d'un grand nombre d'effets environnementaux[64].
Les courbes de croissance données par l'OMS, et présentes par exemple dans les carnets de santé, sont issues de modélisations grâce à une loi normale. Grâce à une étude détaillée des centiles mesurés dans une population d'âge fixé et grâce à des tests statistiques d'adéquation, les répartitions du poids et de la taille par tranche d'âge ont été modélisées par des lois de probabilité. Parmi ces lois on retrouve les lois normales, la loi normale de Box-Cox (en) (généralisation de la loi normale), la loi Student de Box-Cox (généralisation de la loi normale de Box-Cox) ou encore la loi exponentielle-puissance de Box-Cox[a 20]. Graphiquement, pour chaque âge, c'est-à-dire pour chaque axe vertical, la médiane m est représentée (elle donne la courbe centrale) et les deux valeurs de m + σ et m – σ où σ est l'écart type, donnent les deux courbes et ainsi représentent l'évolution d'un intervalle de fluctuation.[réf. nécessaire]
Traitement du signal et mesures physiques
[modifier | modifier le code]
Lorsqu'un signal est transmis, une perte d'information apparaît à cause du moyen de transmission ou du décodage du signal. Lorsqu'une mesure physique est effectuée, une incertitude sur le résultat peut provenir d'une imprécision de l'appareil de mesure ou d'une impossibilité à obtenir la valeur théorique. Une méthode pour modéliser de tels phénomènes est de considérer un modèle déterministe (non aléatoire) pour le signal ou la mesure et d'y ajouter ou multiplier un terme aléatoire qui représente la perturbation aléatoire, parfois appelée erreur ou bruit. Dans beaucoup de cas cette erreur additive est supposée de loi normale, de loi log-normale dans le cas multiplicatif[65]. C'est le cas, par exemple, pour la transmission d'un signal à travers un câble électrique[30]. Lorsque le processus dépend du temps, le signal ou la mesure est alors modélisé grâce à un bruit blanc (voir ci-dessus)[66].
En traitement d'images, une loi normale est utilisée pour améliorer les images et notamment diminuer le bruit, c'est-à-dire les imperfections de l'image. Un lissage grâce à un filtre gaussien est alors utilisé.[réf. nécessaire]
Économie
[modifier | modifier le code]Les prix de certaines denrées sont données par une bourse, c'est le cas du cours du blé, du coton brut ou de l'or. Au temps , le prix évolue jusqu'au temps par l'accroissement . En 1900, Louis Bachelier postule que cet accroissement suit une loi normale de moyenne nulle et dont la variance dépend de et . Cependant ce modèle satisfait peu l'observation faite des marchés financiers. D'autres mathématiciens proposent alors d'améliorer ce modèle en supposant que c'est l'accroissement qui suit une loi normale[a 7], c'est-à-dire que l'accroissement du prix suit une loi log-normale. Cette hypothèse est à la base du modèle et de la formule de Black-Scholes utilisés massivement par l'industrie financière.
Ce modèle est encore amélioré, par Benoît Mandelbrot notamment, en supposant que l'accroissement suit une loi stable (la loi normale est un cas particulier de loi stable). Il apparaît alors le mouvement brownien dont l'accroissement est de loi normale et le processus de Lévy (stable) dont l'accroissement stable pour modéliser les courbes des marchés[a 7].
Mathématiques
[modifier | modifier le code]
Les lois normales sont utilisées dans plusieurs domaines des mathématiques. Le bruit blanc gaussien est un processus stochastique tel qu'en tout point, le processus est une variable aléatoire de loi normale indépendante du processus aux autres points[67]. Le mouvement brownien est un processus stochastique dont les accroissements sont indépendants, stationnaires et de loi normale[a 7]. Notamment pour une valeur fixée, la variable aléatoire suit la loi normale . Ce processus aléatoire possède de nombreuses applications, il fait un lien entre l'équation de la chaleur et la loi normale[a 3]. Lorsque l'extrémité d'une tige métallique est chauffée pendant un court instant, la chaleur se propage le long de la tige sous la forme d'une courbe en cloche.
Les lois normales ont également des applications dans des domaines mathématiques non aléatoires comme la théorie des nombres. Tout nombre entier n peut s'écrire comme un produit de puissances de nombres premiers. Notons le nombre de nombres premiers différents dans cette décomposition. Par exemple, puisque , . Le théorème d'Erdős-Kac assure[a 3] que cette fonction pour est apparentée à la densité d'une loi normale . C'est-à-dire que pour un grand nombre de l'ordre de , il y a une forte probabilité pour que le nombre de diviseurs premiers soit 3, puisque .
Tests et estimations
[modifier | modifier le code]Critères de normalité
[modifier | modifier le code]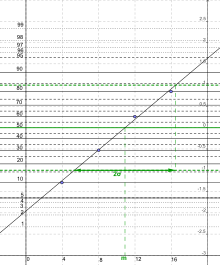
La droite de Henry permet de faire un ajustement des valeurs observées avec une loi normale. C'est-à-dire qu'en représentant la droite de Henry, il est possible de porter un diagnostic sur la nature normale ou non de la distribution et, dans le cas où celle-ci a des chances d'être normale, elle permet d'en déterminer la moyenne et l'écart type. Les valeurs sont observées et représentées par leur fonction de répartition empirique . Elles sont gaussiennes si les points représentés sur un papier gausso-arithmétique sont alignés suivant une droite dite de Henri[68]. Un papier gausso-arithmétique est gradué avec une échelle arithmétique en abscisse et graduée suivant l'inverse de la fonction de répartition de la loi normale centrée réduite en ordonnée[69].
Ces critères sont nécessaires mais non suffisants. Cependant, il ne suffit pas de remplir les critères pour affirmer que les valeurs suivent la loi normale.[réf. nécessaire]
Tests de normalité
[modifier | modifier le code]Grâce à son rôle dans le théorème central limite, les lois normales se retrouvent dans de nombreux tests statistiques dits gaussiens ou asymptotiquement gaussiens. L'hypothèse dite de normalité est faite sur une loi a priori dans un test d'adéquation pour indiquer que cette loi suit, approximativement, une loi normale[a 18]. Il existe plusieurs tests de normalité.
- Un test du χ2 d'adéquation à une loi normale est possible pour tester si une série de k valeurs observées suit une loi normale[70]. Dans ce type de test, l'hypothèse nulle est : la distribution observée peut être approchée par une loi normale. Après avoir regroupé les k valeurs observées en classes, il faut calculer les probabilités qu'une variable aléatoire de loi normale appartienne à chaque classe en estimant les paramètres de la loi grâce aux valeurs observées. Ces probabilités peuvent être obtenues avec les tables numériques d'une loi normale. Si l'hypothèse nulle est vraie, la statistique du χ2 calculée à partir des valeurs observées et des probabilités précédentes suit une loi du χ². Le nombre de degré de liberté est k – 1 si la moyenne et l'écart type sont connus, k – 2 si l'un des deux paramètres est inconnu, ou k – 3 si les deux paramètres sont inconnus. L'hypothèse nulle est rejetée si la statistique du χ2 est supérieure à la valeur obtenue grâce à la table de la loi du χ2 au seuil α.
- Le test de Lilliefors est basé sur la comparaison entre la fonction de répartition d'une loi normale et la fonction de répartition empirique, c'est une adaptation du test de Kolmogorov-Smirnov. Les avis sont partagés sur la puissance de ce test, il est performant autour de la moyenne mais l'est moins pour la comparaison des queues de distribution[a 21]. Les valeurs observées sont rangées par ordre croissant , les valeurs sont les fréquences théoriques de la loi normale centrée réduite associées aux valeurs standardisées. Si la statistique :est supérieure à une valeur critique calculée grâce au seuil α et à la taille de l'échantillon, alors l'hypothèse de normalité est rejetée au seuil α.
- Le test d'Anderson-Darling est une autre version du test de Kolmogorov-Smirnov mieux adaptée à l'étude des queues de distribution[a 21]. En reprenant les mêmes notations que le test de Lilliefors, si la statistique :est supérieure à une valeur critique calculée grâce au seuil α et à la taille de l'échantillon, alors l'hypothèse de normalité est rejetée au seuil α.
- Le test de D'Agostino est basé sur les coefficients de symétrie et d'aplatissement. Il est particulièrement efficace à partir de valeurs observées[a 21]. Même si l'idée de ce test est simple, les formules sont plus compliquées à écrire. L'idée est de construire des modifications des coefficients de symétrie et d'aplatissement pour obtenir des variables et de loi normale centrée réduite. Il faut alors effectuer un test du χ² avec la statistique .
- Le test de Jarque-Bera est également basé sur les coefficients de symétrie et d'aplatissement. Ce test n'est intéressant que pour un nombre élevé de valeurs observées[a 21]. En considérant les deux estimateurs : et comme précédemment, il faut effectuer un test du χ2 avec la statistique .
- Le test de Shapiro-Wilk (proposé en 1965) est efficace pour les petits échantillons de moins de 50 valeurs[a 21]. Les valeurs observées sont rangées par ordre croissant et des coefficients sont calculés à partir de quantiles, moyenne, variance et covariance d'une loi normale. Si la statistiqueest inférieure à une valeur critique calculée grâce au seuil α et à la taille de l'échantillon, alors l'hypothèse de normalité est rejetée au seuil α.
Estimations des paramètres
[modifier | modifier le code]Lorsqu'un phénomène aléatoire est observé et qu'il est considéré comme pouvant être modélisé par une loi normale, une des questions que l'on peut se poser est : que valent les paramètres μ et σ de la loi normale ? Une estimation est alors à effectuer. Les observations récupérées lors de l'observation du phénomène sont notées par des variables aléatoires , les notations de la moyenne arithmétique et de la moyenne des carrés sont également utiles[71] : et . Ces deux valeurs sont respectivement des estimateurs de la moyenne et de la variance qui se calculent à partir des valeurs observées. Puisque les variables sont de loi normale, alors est de loi et est indépendante de Sn et de loi du χ² à n – 1 degrés de liberté[71].
Estimation de la moyenne μ (lorsque l'écart type σ est connu)
[modifier | modifier le code]Une méthode est de chercher un intervalle de confiance à un seuil α autour de la moyenne théorique μ. En utilisant les quantiles d'ordre et , la formule définissant les quantiles permet d'obtenir[71] : . Grâce aux valeurs observées et aux tables numériques de la loi normale centrée réduite (voir la table), il est alors possible de donner les valeurs numériques de l'intervalle , intervalle de confiance pour μ au seuil α.
Estimation de la moyenne μ (lorsque l'écart type σ est inconnu)
[modifier | modifier le code]Une méthode est d'utiliser une variable intermédiaire qui peut s'écrire à l'aide de nouvelles variables aléatoires de loi et de loi : est de loi de Student . En utilisant les quantiles d'ordre et , la formule définissant les quantiles permet d'obtenir[72] : . Grâce aux valeurs observées et aux tables numériques des lois de Student, il est alors possible de donner les valeurs numériques de l'intervalle , intervalle de confiance pour μ au seuil α.
Estimation de l'écart type σ (lorsque la moyenne μ est inconnue)
[modifier | modifier le code]La méthode est la même que la précédente. L'introduction de la variable aléatoire de loi du χ² à n – 1 degrés de liberté permet d'obtenir[73] : où et sont les quantiles de la loi du χ2 à n – 1 degrés de liberté que l'on peut obtenir à partir de la table numérique du χ2. L'intervalle est l'intervalle de confiance au seuil α.
Simulation
[modifier | modifier le code]Pour étudier un phénomène aléatoire dans lequel intervient une variable normale dont les paramètres sont connus ou estimés, une approche analytique est souvent trop complexe à développer. Dans un tel cas, il est possible de recourir à une méthode de simulation, en particulier à la méthode de Monte-Carlo qui consiste à générer un échantillon artificiel de valeurs indépendantes de la variable, ceci à l'aide d'un ordinateur. Les logiciels ou les langages de programmation possèdent en général un générateur de nombres pseudo-aléatoires ayant une distribution uniforme sur ]0, 1[. Il s'agit alors de transformer cette variable de loi en une variable (l'adaptation à d'autres valeurs des paramètres ne pose pas de problème).
Approches à éviter
[modifier | modifier le code]- De manière générale, on peut exploiter la fonction réciproque de la fonction de répartition : en l'occurrence, la variable aléatoire suit la loi normale centrée réduite ; cette méthode est cependant malcommode, faute d'expressions simples des fonctions et ; par ailleurs, les résultats sont numériquement insatisfaisants.
- Si sont douze variables indépendantes de loi uniforme sur [0, 1], alors la variable est de moyenne nulle et d'écart type unitaire. Ainsi, grâce au théorème central limite, cette variable suit approximativement la loi normale centrée réduite[a 22]. C'est une manière simple de générer une loi normale, cependant l'approximation reste imprécise.
Approches efficientes
[modifier | modifier le code]- Un meilleur algorithme est la méthode de Box-Muller qui utilise une représentation polaire de deux coordonnées uniformes donnée par les formules : Si alors et les deux variables obtenues sont indépendantes. Cet algorithme est simple à réaliser, mais le calcul d'un logarithme, d'une racine carrée et d'une fonction trigonométrique ralentit le traitement[a 22].
- Une amélioration a été proposée par Marsaglia et Bray en 1964[a 23], en remplaçant les cosinus et sinus par les variables et où et sont indépendantes de loi et , lorsque (on rejette les couples qui ne vérifient pas cette dernière condition). Ainsi :Cet algorithme n'est pas plus lourd à mettre en œuvre et la simulation gagne en vitesse[a 22].
- Pour un grand nombre de tirages aléatoires, la méthode Ziggourat est encore plus rapide, mais sa mise en œuvre est plus complexe.
Hommages
[modifier | modifier le code]Par son utilisation généralisée dans les sciences, une loi normale, souvent par l'utilisation de la courbe en cloche, est mise en avant dans différents contextes et est utilisée pour représenter l'universalité d'une répartition statistique, entre autres.
Francis Galton parle des lois normales dans son œuvre Natural Inheritence de 1889 en ces termes élogieux[a 2] :
« Je ne connais rien d'autre si propre à frapper l'imagination que cette merveilleuse forme d'ordre cosmique donnée par la Loi de Fréquence des Erreurs... Elle règne avec sérénité et en toute abnégation au milieu de la confusion sauvage[b 4]. »
En 1989, un hommage est rendu à Carl Friedrich Gauss en imprimant un billet à son effigie, la courbe en cloche est également présente sur le billet. Des pierres tombales portent le signe de la courbe en cloche, c'est le cas pour certains mathématiciens.
| Le statisticien William J. Youden écrit[74] en 1962 une explication du but et de la position des lois normales dans les sciences. Il la présente en calligramme sous forme de courbe en cloche : |
THE |
|
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- Pour une généralisation, voir la section Moments ci-dessous.
- Pour son calcul à partir de la densité, voir aussi le lien en bas de page vers la leçon sur Wikiversité.
- Voir par exemple le lien en bas de page vers la leçon sur Wikiversité.
- Initialement en anglais : « I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the Law of Frequency of Error... It reigns with serenity and in complete self-effacement amidst the wildest confusion. »
Références
[modifier | modifier le code]Ouvrages
[modifier | modifier le code]- Dodge 2004, p. 310.
- Quinio Benamo 2005, p. 36.
- Grinstead et Snell 1997, p. 351.
- Béatrice Beaufils, Statistiques appliquées à la psychologie, Volume 2, Bréal, (présentation en ligne), p. 50
- Gilbert Saporta, Probabilités, analyse des données et statistique, TECHNip, (lire en ligne), p. 43
- « Planche de Galton », sur sorciersdesalem.math.cnrs.fr (consulté le ).
- Grinstead et Snell 1997, p. 212.
- Protassov 2002, p. 30.
- Protassov 2002, p. 29.
- Stigler 1999, p. 407.
- Stigler 1999, p. 406.
- Voir par exemple Paul Lévy, Théorie de l'addition des variables aléatoires, Gauthier-Villars, , p. 42 ou, plus récemment, Michel Lejeune, Analyse statistique des données spatiales, Technip, (ISBN 9782710808732), p. 2.
- NBS 1952.
- Dodge 2004, p. 502.
- Lifshits 1995, p. 1.
- Dodge 2004, p. 309.
- Lifshits 1995, p. 2.
- Cramér 1970, p. 50.
- Tassi et Legait 1990, p. 128.
- Grinstead et Snell 1997, p. 330.
- Droesbeke, Lejeune et Saporta 2005, p. 104.
- Bogaert 2006, p. 121.
- Bogaert 2006, p. 123.
- Protassov 2002, p. 27.
- Cramér 1970, p. 51.
- Ross 2007, p. 408.
- Protassov 2002, p. 27, utilise le changement de variable .
- Quinio Benamo 2005, p. 1699.
- Bogaert 2006, p. 116.
- Ross 2007, p. 239.
- Protassov 2002, p. 28.
- Droesbeke, Lejeune et Saporta 2005, p. 85.
- Bogaert 2006, p. 120.
- Bogaert 2006, p. 119.
- Abramowitz et Stegun 1972, p. 930.
- Grinstead et Snell 1997, p. 345.
- Protassov 2002, p. 44.
- Bogaert 2006, p. 223.
- Ross 2007, p. 240.
- Yger et Weil 2009, p. 651.
- Ross 2007, p. 299.
- Lifshits 1995, p. 4.
- Cramér 1970, p. 52.
- Cramér 1970, p. 53.
- Ross 2007, p. 235.
- Lifshits 1995, p. 125.
- Abramowitz et Stegun 1972, p. 932.
- Tassi et Legait 1990, p. 126.
- Bogaert 2006, p. 354.
- Grinstead et Snell 1997, p. 213.
- Grinstead et Snell 1997, p. 214.
- Protassov 2002, p. 72.
- Bogaert 2006, p. 90.
- Ross 2007, p. 301.
- Yger et Weil 2009, p. 703.
- Bogaert 2006, p. 330.
- Bogaert 2006, p. 341.
- Hosking et Wallis 1997, p. 197.
- Bogaert 2006, p. 86.
- Tassi et Legait 1990, p. 205.
- Bogaert 2006, p. 68.
- Ridley 2004, p. 76.
- Ridley 2004, p. 226.
- Ridley 2004, p. 252.
- Hosking et Wallis 1997, p. 157.
- Dodge 2004, p. 354.
- Yger et Weil 2009, p. 573.
- Tassi et Legait 1990, p. 144.
- Dodge 2004, p. 228.
- Dodge 2004, p. 519.
- Yger et Weil 2009, p. 715.
- Yger et Weil 2009, p. 716.
- Yger et Weil 2009, p. 717.
- Stigler 1999, p. 415.
Articles et autres sources
[modifier | modifier le code]- Bernard Bru, « La courbe de Gauss ou le théorème de Bernoulli raconté aux enfants », Mathematics and Social Sciences, vol. 175, no 3, , p. 5-23 (lire en ligne).
- Aimé Fuchs, « Plaidoyer pour la loi normale », Pour la Science, , p. 17 (lire en ligne [PDF]).
- Jean-Pierre Kahane, « La courbe en cloche », sur Images des maths, CNRS, .
- (en) George Marsaglia, « Evaluating the Normal Distribution », Journal of Statistical Software, vol. 11, no 4, , p. 1-11 (DOI 10.18637/jss.v011.i04).
- Ministère de l'éducation nationale de la jeunesse et de la vie associative, Ressources pour la classe terminale générale et technologique - Probabilités et statistique, (lire en ligne [PDF]).
- (en) Eric W. Weisstein, « Gaussian Function », sur MathWorld.
- Benoît Mandelbrot, « Nouveaux modèles de la variation des prix (Cycles lents et changements instantanés) », Cahiers du Séminaire d'Économétrie, no 9, , p. 53-66 (JSTOR 20075411).
- (en) Claude Shannon, « A Mathematical Theory of Communication », The Bell System Technical Journal, vol. 27, , p. 379-423.
- (en) Lloyd Allison, « Normal, Gaussian », .
- (en) Eric W. Weisstein, « Normal Distribution Function », sur MathWorld.
- Nicolas Ferrari, « Prévoir l'investissement des entreprises Un indicateur des révisions dans l'enquête Investissement », Économie et Statistique, nos 395-396, , p. 39-64 (lire en ligne).
- T. Pham-Gia, N. Turkkan et E. Marchand, « Density of the Ratio of Two Normal Random Variables and Applications », Communications in Statistics - Theory and Methods, vol. 35, , p. 1569–1591 (ISSN 0361-0926, DOI 10.1080/03610920600683689)
- (en) Liang Faming, « A robust sequential Bayesian method for identification of differentially expressed genes », Statistica Sinica, vol. 17, no 2, , p. 571-597 (lire en ligne).
- (en) Norbert Henze, « A Probabilistic Representation of the 'Skew-Normal' Distribution », Scandinavian Journal of Statistics, vol. 13, no 4, , p. 271-275 (JSTOR 4616036).
- G Rouzet, « Étude des moments de la loi normale tronquée », Revue de statistique appliquée, vol. 10, no 2, , p. 49-61 (lire en ligne).
- (en) Sepp Hochreiter, Djork-Arne Clevert et Klaus Obermayer, « A new summarization method for affymetrix probe level data », Bioinformatics, vol. 22, no 8, , p. 943-949 (DOI 10.1093/bioinformatics/btl033).
- (en) Richard Irvine, « A Geometrical Approach to Conflict Probability Estimation », Air Traffic Control Quarterly seminar, vol. 10, no 2, , p. 1-15 (DOI 10.2514/atcq.10.2.85).
- Nacira Hadjadji Seddik-Ameur, « Les tests de normalité de Lhoste », Mathematics and Social Sciences, vol. 41, no 162, , p. 19-43 (lire en ligne).
- Suzanne Mollo, « Tort (Michel). — Le quotient intellectuel », Revue française de pédagogie, vol. 33, no 33, , p. 66-68 (lire en ligne).
- (en) Borghi, de Onis, Garza, Van den Broeck, Frongillo, Grummer-Strawn, Van Buuren, Pan, Molinari, Martorell, Onyango1 et Martines, « Construction of the World Health Organization child growth standards: selection of methods for attained growth curves », Statistics in medecine, vol. 25, , p. 247-265 (DOI 10.1002/sim.2227).
- Ricco Rakotomalala, « Tests de normalité » [PDF], .
- (en) A. C. Atkinson et M. C. Pearce, « The Computer Generation of Beta, Gamma and Normal Random Variables », Journal of the Royal Statistical Society, vol. 139, no 4, , p. 431-461 (JSTOR 2344349).
- (en) George Marsaglia et Thomas A. Bray, « A convenient method for generating normal variables », SIAM Review, vol. 6, no 3, juillet 1964, p. 260-264 (JSTOR:2027592, DOI 10.1137/1006063).
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions, New York, Dover, , 9e éd., 1047 p. (ISBN 0-486-61272-4, lire en ligne), chap. 26 (« Probability Functions »), p. 927-996

- Patrick Bogaert, Probabilités pour scientifiques et ingénieurs, Paris, De Boeck, , 387 p. (ISBN 2-8041-4794-0, lire en ligne)

- (en) Harald Cramér, Random Variables and Probability Distributions, Cambridge University Press, , 3e éd., 123 p. (ISBN 0-521-60486-9, lire en ligne)

- Yadolah Dodge (en), Statistique - dictionnaire encyclopédique, Springer Verlag, , 637 p. (ISBN 2-287-21325-2, lire en ligne)

- Jean-Jacques Droesbeke, Michel Lejeune et Gilbert Saporta, Modèles statistiques pour données qualitatives, Technip, , 295 p. (ISBN 2-7108-0855-2, lire en ligne)

- (en) Joseph Arthur Greenwood et H. O. Hartley, Guide to Tables in Mathematical Statistics, Princeton University Press, , 1014 p.

- (en) Charles Miller Grinstead et James Laurie Snell, Introduction to Probability, AMS, , 2e éd., 519 p. (ISBN 0-8218-0749-8, lire en ligne)

- (en) J. R. M. Hosking et James R. Wallis, Regional Frequency Analysis: An Approach Based on L-Moments, Cambridge University Press, , 224 p. (ISBN 978-0-521-43045-6, lire en ligne)

- (en) M. A. Lifshits, Gaussian Random Functions, Kluwer Academic Publishers, , 339 p. (ISBN 0-7923-3385-3, lire en ligne)

- (en) NBS, A Guide to Tables of the Normal Probability Integral, U.S. Govt. Print. Off., , 16 p.

- Konstantin Protassov, Analyse statistique des données expérimentales, EDP Sciences, , 148 p. (ISBN 978-2-75980113-8, lire en ligne)

- Martine Quinio Benamo, Probabilités et Statistique aujourd'hui, L'Harmattan, , 277 p. (ISBN 2-7475-9799-7, lire en ligne)

- (en) Mark Ridley (en), Evolution, Blackwell, , 3e éd., 751 p. (ISBN 1-4051-0345-0)

- Sheldon M. Ross, Initiation aux probabilités, PPUR, , 592 p. (ISBN 978-2-88074-738-1, lire en ligne)

- (en) Stephen Stigler, Statistics on the Table, Harvard University Press, , 499 p. (ISBN 0-674-83601-4, lire en ligne)

- Philippe Tassi et Sylvia Legait, Théorie des probabilités en vue des applications statistiques, Technip, , 367 p. (ISBN 2-7108-0582-0, lire en ligne)

- Alain Yger et Jacques-Arthur Weil, Mathématiques appliquées, Pearson Education, , 890 p. (ISBN 978-2-7440-7352-6, lire en ligne)

Articles connexes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]
- Ressources relatives à la santé :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- (en) Generating Gaussian Random Numbers
- Dix vidéos (sur YouTube) de moins de dix minutes chacune dans lesquelles Saïd Chermak explique les propriétés de la loi normale.
- Animation en ligne de la planche de Galton.






























![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \mathbb {P} (X\in [a,b])=\Phi (b)-\Phi (a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34021ca68e186eb6321321cf619fd9271e0c3129)



























![{\displaystyle {\begin{cases}\mu _{2k}=\mathbb {E} [(X-\mu )^{2k}]={\frac {(2\,k)!}{2^{k}k!}}\sigma ^{2k}\\\mu _{2k+1}=\mathbb {E} [(X-\mu )^{2k+1}]=0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd628c31049cf70f610ffc9f03b66f891c219593)

![{\displaystyle m_{1}=\mathbb {E} [X]=\mu ,\quad m_{2}=\mathbb {E} [X^{2}]=\sigma ^{2}+\mu ^{2},\quad m_{3}=\mathbb {E} [X^{3}]=3\mu \sigma ^{2}+\mu ^{3},\quad m_{4}=\mathbb {E} [X^{4}]=3\sigma ^{4}+6\sigma ^{2}\mu ^{2}+\mu ^{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5e3f8b72cd9f1d4228d7d4732b95f8c64cd1b4f)








![{\displaystyle \lim _{n\to +\infty }\mathbb {P} \left(a\leq {\frac {S_{n}-\mathbb {E} [S_{n}]}{\sqrt {\operatorname {Var} (S_{n})}}}\leq b\right)=\int _{a}^{b}\varphi (x)\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/289614888af33a15c1fc4c9bfcefd4807650080a)









![{\displaystyle \sum _{1\leq k\leq n}\mathbb {E} [X_{nk}^{\varepsilon }]{\underset {n\to \infty }{\longrightarrow }}\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c521d48c6f3d1b168c5a08700ae0a1b12a4f1550)
![{\displaystyle \sum _{1\leq k\leq n}{\text{Var}}[X_{nk}^{\varepsilon }]{\underset {n\to \infty }{\longrightarrow }}\sigma ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86182adeee3cbfb4d3d617cbc9aa131bcf0600ba)


























![{\displaystyle \lambda \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/350ab5a5c7b6824da0369a91495c3733e9fc3e51)






















![{\displaystyle \Phi (x)=\mathbb {P} [X\leq x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b902c94ed7f70be63a1dc3bc78403187964686a)
![{\displaystyle \mathbb {P} [X\leq x]=\Phi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95122ee20b4c0ef57ae4c372bd56c6fd59ce6403)
![{\displaystyle \mathbb {P} [x_{1}\leq X\leq x_{2}]=\Phi (x_{2})-\Phi (x_{1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9df5134019663eb35489d7813df4a9f2b4342155)
![{\displaystyle \mathbb {P} [X\geq x]=1-\Phi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/936e5cdd2829f4ebd431e745568bc774cdf1fd36)




![{\displaystyle \Phi (-1{,}07)=\mathbb {P} [X\leq -1{,}07]\approx 1-0{,}85769=0{,}14231}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e28fec54449a210ca78fea1875cf485ef822dd8d)

![{\displaystyle F(12{,}14)=\mathbb {P} [Y\leq 12{,}14]=\mathbb {P} \left[{\frac {Y-10}{2}}\leq {\frac {12{,}14-10}{2}}\right]=\mathbb {P} [X\leq 1{,}07]=\Phi (1{,}07)\approx 0{,}85769}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d421e74bb272b6b2405d97e323ab7ad6c9a4b15)

![{\displaystyle \mathbb {P} \left[X\in [a,b]\right]=\mathbb {P} [X\leq b]-\mathbb {P} [X<a]=\Phi (b)-\Phi (a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43802002ca92e7d9ba293f17a9614c1b63f976a8)
![{\displaystyle \mathbb {P} [X\geq 1{,}07]=1-\mathbb {P} [X<1{,}07]=1-\mathbb {P} [X\leq 1{,}07]\approx 0{,}14231}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff4d4433db689c5347240c41a63d0c0740cf6537)
![{\displaystyle \mathbb {P} [0\leq X\leq 1{,}07]=\Phi (1{,}07)-\Phi (0)=\Phi (1{,}07)-0{,}5\approx 0{,}85769-0{,}5=0{,}35769}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dee55f86f740d527024ae096fbaf5edca677820)
![{\displaystyle \mathbb {P} [\mu -r\sigma \leq Y\leq \mu +r\sigma ]=\Phi (r)-(1-\Phi (r))=2\Phi (r)-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048de424a42579d8e7e362f003ef2b279e597912)

![{\displaystyle \mathbb {P} _{r}=\mathbb {P} [\mu -r\sigma \leq Y\leq \mu +r\sigma ]=2\Phi (r)-1{\text{ pour }}Y\sim {\mathcal {N}}(\mu ,\sigma ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb842f6f3a803967645114f1b6a4846bcf797db1)





















































![{\displaystyle [-T,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b8466d3122dfdddcf0f209fc31dd4d3e05e5797)
![{\displaystyle f(x)={\begin{cases}{\frac {\varphi (x)}{2\Phi (T)-1}}&{\text{ si }}x\in [-T,T]\\0&{\text{ sinon }}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dca40ef52c7f31ec2bca16a485f46d662c6fe1b)

![{\displaystyle \left]-\infty ,0\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10c3a4dbadb446d3509e7d7f25654de172d94be)




![{\displaystyle y={\begin{cases}-{\frac {1}{\kappa }}\log \left[1-{\frac {\kappa (x-\xi )}{\alpha }}\right]&{\text{si }}\kappa \neq 0\\{\frac {x-\xi }{\alpha }}&{\text{si }}\kappa =0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52c96fd7a5dac8725c708e78422ac99d122dc749)



























![{\displaystyle [{\overline {x}}-\sigma ,{\overline {x}}+\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c534244472d6825d6ef6124033cd2d2a4b628a9)
![{\displaystyle [{\overline {x}}-2\sigma ,{\overline {x}}+2\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53013db6884428283cf8118fcd0c05348aa6b8f9)
![{\displaystyle [{\overline {x}}-3\sigma ,{\overline {x}}+3\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604dfd7cc3787b7d8ed4347e689c7a61c9f6a944)
















![{\displaystyle W={\frac {\left(\sum _{i=1}^{[n/2]}a_{i}\left(x_{(n-i+1)}-x_{(i)}\right)\right)^{2}}{\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76e9c8f42ccddaf51b54368243ebede538f072d2)








![{\displaystyle \left[S_{n}-{\frac {\sigma }{\sqrt {n}}}q_{\alpha /2},S_{n}+{\frac {\sigma }{\sqrt {n}}}q_{\alpha /2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b313d07dc393ba05ca7cb7ae9ca4566d2351005)






![{\displaystyle \left[S_{n}+{\frac {T_{n-1}}{\sqrt {n}}}q_{\alpha /2},S_{n}-{\frac {T_{n-1}}{\sqrt {n}}}q_{\alpha /2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/683fda327833aa24769e63b7f6ecaa4c95be5bbc)




![{\displaystyle \left[{\sqrt {T_{n-1}^{2}{\frac {n-1}{q_{1-\alpha /2}}}}},{\sqrt {T_{n-1}^{2}{\frac {n-1}{q_{\alpha /2}}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ec5654f412abfe04ede957b5cd64e4760fdcd55)
![{\displaystyle U(]0,1[)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f3e37443fa018b86b01c399ee00e07db10416a3)













