Loi du χ²

Pour les méthodes expérimentales, voir Test du χ² et méthode des moindres carrés.

Loi du χ2
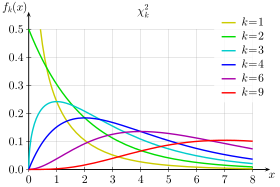Densité de probabilité (ou fonction de masse)
Fonction de répartition
Paramètres	$k \in \N^*$ degrés de liberté
Support	$x \in [0, +\infty[\,$
Densité de probabilité (fonction de masse)	$\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}\,$ où $\Gamma$ est la fonction gamma
Fonction de répartition	$\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}\,$ où $\gamma$ est la fonction gamma incomplète
Espérance	$k\,$
Médiane	$\approx k-2/3\,$
Mode	$k-2\,$ si $k\geq 2\,$
Variance	$2\,k\,$
Asymétrie	$\sqrt{8/k}\,$
Kurtosis normalisé	$\frac{12}{k}\,$
Entropie	$\frac{k}{2}\!+\!\ln(2\Gamma(k/2))\!+\!(1\!-\!k/2)\psi(k/2)$
Fonction génératrice des moments	$(1-2\,t)^{-k/2}$ pour $2\,t<1\,$
Fonction caractéristique	$(1-2\,i\,t)^{-k/2}\,$

La loi du χ² (prononcer « khi-deux » ou « khi carré ») est une loi à densité de probabilité. Cette loi est caractérisée par un paramètre dit degrés de liberté à valeur dans l'ensemble des entiers naturels (non nuls).

Soient $\scriptstyle X_1, \ldots , X_k$, k variables aléatoires indépendantes suivant des lois normales de moyennes respectives $\mu_i$ et d'écart-type $\sigma_i$ ; $\scriptstyle Y_i=\frac{X_i-\mu_i}{\sigma_i}$ leurs variables centrées et réduites, alors par définition la variable $X \$, telle que

$X: \ =\sum_{i=1}^k Y_i^2=\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2$

suit une loi du χ² à k degrés de liberté.

Soit $X~$ une variable aléatoire suivant une loi du χ² à $k~$ degrés de liberté, on notera $\chi^2(k)~$ la loi de $X~$.

Alors la densité de $X~$ notée $f_X~$ sera :

$f_X(t)=\frac{1}{2^\frac{k}{2}\Gamma(\frac{k}{2})} t^{\frac{k}{2} - 1} e^{-\frac{t}{2}}\,$ pour tout t positif

où Γ est la fonction gamma.

L'espérance mathématique de $X$ vaut $k$ et sa variance vaut $2k$.

Approximation

Conformément au théorème central limite , lorsque k est « grand » (k > 100), la loi d'une variable de χ², somme de variables aléatoires indépendantes, peut être approchée par une loi normale d'espérance k et de variance 2k.

D'autres fonctions en χ² peuvent converger plus rapidement vers la loi normale, notamment en ayant X~χ²(k) et k>30 :

• $\scriptstyle\sqrt{2X} - \sqrt{(2k-1)}$ peut être approchée par une loi normale centrée réduite (Ronald Aylmer Fisher).
• $\scriptstyle\sqrt[3]{X/k}$ peut être approchée par une loi normale de moyenne $\scriptstyle 1-2/(9k)$ et de variance $\scriptstyle 2/(9k)$ (Wilson et Hilferty, 1931).

Utilisation

La principale utilisation de cette loi consiste à apprécier l'adéquation d'une loi de probabilité à une distribution empirique en utilisant le test du χ² basé sur la loi multinomiale. Plus généralement elle s'applique dans le test d'hypothèses à certains seuils (indépendance notamment).

Liens avec d'autres lois

Soient $X_i$ des variables aléatoires indépendantes suivant des lois normales d'espérance $\mu_i$ et de variance $\sigma_i^2$.

Différentes lois du $\chi$ et $\chi^2$

Lois	en fonction de variables de loi normale
loi du χ2	$\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2$
Loi du χ² non centrée	$\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2$
loi du χ	$\sqrt{\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2}$
loi du χ non centrée	$\sqrt{\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2}$

Si X une variable aléatoire de loi normale centrée et réduite et Y suit une loi du $\chi^2$ à n degrés de liberté, X et Y étant indépendantes, alors $\frac{X}{\sqrt{Y/n}}$ suit une loi de Student à n degrés de liberté.

Si X suit une loi du $\chi^2$ à n degré de liberté, et Y une loi du $\chi^2$ à m degrés de liberté, et si X et Y sont indépendantes, alors $\frac{X/n}{Y/m}$ suit une loi de Fisher à n et m degrés de liberté.

Lien avec les méthodes bayésiennes

Dans son ouvrage Décisions rationnelles dans l'incertain (1974), qui constitue une somme des techniques bayésiennes dont la grande émergence se fait à cette époque, le professeur Myron Tribus montre que le χ² constitue un exemple de passage à la limite du psi-test (test de plausibilité) bayésien lorsque le nombre de valeurs en présence devient grand - ce qui est la condition de travail des statistiques classiques, mais pas nécessairement des bayésiennes. Le raccord entre les deux disciplines, qui sont asymptotiquement convergentes, est ainsi complet.

L'ouvrage de référence de Jaynes en donne également une démonstration en page 287.

Voir aussi

Articles connexes

• Loi Gamma
• Loi de Rice
• Méthode des moindres carrés
• Test du χ²

Bibliographie

• H. O. Lancaster (1969) The Chi-squared Distribution, New York: Wiley.