Puissance statistique
Cet article est une ébauche concernant les probabilités et la statistique et la médecine.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
La puissance statistique d'un test est en statistique la probabilité de rejeter l'hypothèse nulle (par exemple l'hypothèse selon laquelle les groupes sont identiques au regard d'une variable) sachant que l'hypothèse nulle est incorrecte (en réalité les groupes sont différents). On peut l'exprimer sous la forme 1-β où β est le risque de 2e espèce c'est-à-dire le risque de ne pas démontrer que deux groupes sont différents alors qu'ils le sont dans la réalité.
Par exemple, dans le cadre d'une étude randomisée en double aveugle pour le développement d'un nouveau médicament, le risque de 2e espèce β peut être la probabilité de conclure qu'un médicament n'est pas meilleur qu'un placebo alors qu'il l'est. Dans ce cas, la puissance du test serait la probabilité de conclure que le médicament est meilleur que le placébo, ce qui est vrai.
Description[modifier | modifier le code]
La puissance dépend du nombre de sujets inclus, du risque de première espèce (α) et de la taille de l'effet (différence entre les deux groupes pour un essai clinique) relativement aux autres grandeurs d'intérêt (comme la variance).
La puissance statistique consentie permet de calculer le nombre de sujets nécessaires dans une étude. En général, on fixe la puissance désirée, le risque de première espèce et les paramètres associés aux groupes pour obtenir le nombre de sujets nécessaire à l'étude. Le calcul de la puissance statistique peut s'appliquer à grand nombre de tests statistiques (comparaison de moyennes, comparaison de proportions, modèle logistique, modèle de régression…), lorsque l'hypothèse alternative est suffisamment restrictive.
Exemple[modifier | modifier le code]
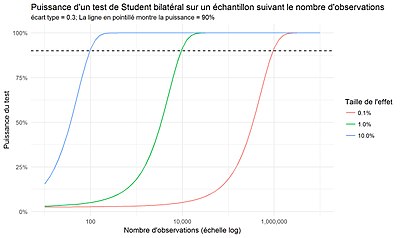
Dans l'exemple suivant, on considère un test de Student bilatéral avec un écart type de 0,3. Pour atteindre une puissance de 0,9 si l'on souhaite une taille d'effet de 10 %, il faut 100 observations.
Références[modifier | modifier le code]
- Michel Cucherat, Lecture critique et interprétation des résultats des essais cliniques pour la pratique médicale, Médecine Sciences Publications, coll. « Nouveaux modules », , 376 p. (ISBN 2-257-11176-1, EAN 9782257111760)
- Voir notamment la section « Puissance et calcul du nombre de sujets nécessaires » dans le document publié sur le Portail numérique de pédagogie des disciplines de santé de l’Université d’Angers : Michel Cucherat, « Interprétation des résultats des essais cliniques pour la pratique médicale », (consulté le ).
- Jacob Cohen, Statistical Power Analysis for the Behavioral Sciences (second ed.), Lawrence Erlbaum Associates, 1988 (ISBN 0-8058-0283-5).
