Variables indépendantes et identiquement distribuées

En théorie des probabilités et en statistique, des variables indépendantes et identiquement distribuées sont des variables aléatoires qui suivent toutes la même loi de probabilité et sont indépendantes. On dit que ce sont des variables aléatoires iid ou plus simplement des variables iid.
Un exemple classique de variables iid apparait lors d'un jeu de pile ou face, c'est-à-dire des lancers successifs d'une même pièce. Les variables aléatoires qui représentent chaque résultat des lancers (0 pour face et 1 pour pile) suivent toutes la même loi de Bernoulli. De plus les lancers étant successifs, les résultats n'ont pas de lien de dépendance entre eux et ainsi les variables aléatoires sont indépendantes.
L'apparition de variables iid se retrouve régulièrement en statistique. En effet, lorsque l'on étudie un caractère sur une population, on réalise un échantillon : on sélectionne une partie de la population, on mesure le caractère étudié et on obtient ainsi une série de valeurs qui sont supposées aléatoires, indépendantes les unes des autres et qui sont modélisées par des variables aléatoires avec une loi de probabilité adaptée. Inversement, lorsque l'on récupère des données statistiques, des méthodes permettent de savoir si elles sont issues de variables iid.
Plusieurs théorèmes de probabilité nécessitent l'hypothèse de variables iid. En particulier le théorème central limite dans sa forme classique énonce que la somme renormalisée de variables iid tend vers une loi normale. C'est également le cas de la loi des grands nombres qui assure que la moyenne de variables iid converge vers l'espérance de la loi de probabilité des variables.
Des méthodes de calcul comme la méthode de Monte-Carlo utilisent des variables iid. Il est alors utile de savoir simuler informatiquement celles-ci ; ces valeurs simulées sont dites pseudo-aléatoires car obtenir des valeurs parfaitement iid est impossible. Les algorithmes utilisant la congruence sur les entiers ne donnent pas d'indépendance parfaite, on parle dans ce cas de hasard faible. En utilisant des phénomènes physiques, il est possible d'obtenir de meilleures valeurs pseudo-aléatoires, il s'agit de hasard fort.
Origines et explications[modifier | modifier le code]
Dans l'histoire des probabilités, les premiers raisonnements tels que le problème des partis au XVIIe siècle, ont été faits sur des jeux de hasard. Il est question d'un jeu en plusieurs parties ; même si le terme de variables indépendantes et identiquement distribuées n'est pas utilisé, il en est question : « le hasard est égal[1] ». Dans le problème du jeu de dés posé par le chevalier de Méré, il admet que « les faces du dé sont également possibles et par là-même qu'elles ont la même chance de se produire[1] ».
C'est toujours au XVIIe siècle que Jérome Cardan, Pierre de Fermat et Christian Huygens utilisent la notion d'équiprobabilité, c'est-à-dire que certains événements ont la même probabilité d'apparaître, autrement dit que certaines variables suivent la même loi. La notion d'indépendance n'apparaît que plus tard avec Abraham de Moivre[2].
Dans les mêmes années, des questions se posent en démographie au sujet des rentes viagères[3]. Ces questions statistiques s'appuient sur les travaux probabilistes naissants des jeux de hasard pour évaluer des valeurs des rentes. Leibniz considère ces questions comme analogues aux jeux de hasard, c'est-à-dire dans le cas d’événements indépendants et de même chance : les fréquences des décès sont considérées comme des valeurs de probabilité, la durée comme le gain dans un jeu contre la nature et les calculs sur plusieurs personnes se font par multiplication[3].
Ainsi les exemples du lancer du dé[4], du jeu de pile ou face[5] ou du tirage aléatoire avec remise de boules dans une urne sont des exemples classiques que l'on modélise par des variables indépendantes et identiquement distribuées. Pour ces trois exemples, chaque tirage ou lancer se fait dans les mêmes situations (même dé, même pièce ou même contenu de l'urne grâce au tirage avec remise), ainsi les résultats de chaque tirage suivent la même loi de probabilité. De plus les tirages ou lancers ne dépendent pas des résultats des tirages et lancers précédents (encore dû à la remise des boules), les variables aléatoires sont donc indépendantes.
En statistique, un échantillon est construit en « tirant au hasard » des individus dans une population[6]. Le terme « au hasard » sous-entend l'hypothèse d'équiprobabilité, c'est-à-dire qu'à chaque tirage, les individus ont la même chance d'être prélevés, ce qui assure que les résultats du tirage sont de même loi. Pour avoir l'indépendance, le tirage peut être réalisé avec remise[7]. Dans le cas où la population totale est très grande ou considérée infinie, le fait de tirer avec ou sans remise ne modifie pas l'indépendance des résultats.
De tels résultats obtenus par plusieurs observations successives d'un même phénomène aléatoire sont appelés des échantillons aléatoires[8].
Définition[modifier | modifier le code]
La désignation « indépendantes et identiquement distribuées » regroupe deux notions : l'indépendance et la loi de probabilité. L'indépendance est une propriété qui régit les relations des variables entre elles, tandis que la notion d'identiquement distribuée se réfère à la faculté de chacune des variables de suivre la même loi de probabilité que les autres variables de la suite. Des variables indépendantes et identiquement distribuées sont dites iid[9], i.i.d[10]. ou indépendantes et équidistribuées.
Intuitivement, dans le cas de variable aléatoire réelle, l'indépendance entre deux variables aléatoires signifie que la connaissance de l'une n'influe en rien sur la valeur de l'autre[9].
Donnons les cas particuliers de deux variables aléatoires discrètes ne pouvant prendre qu'un nombre fini de valeurs, et de deux variables aléatoires continues, c'est-à-dire possédant une densité de probabilité.
Définition (cas discret)[11] — Deux variables aléatoires réelles sont dites indépendantes et identiquement distribuées si elles sont :
- indépendantes,
c'est-à-dire, pour tous réels , - de même loi,
c'est-à-dire pour tout .
Définition (cas continu)[12] — Deux variables aléatoires réelles sont dites indépendantes et identiquement distribuées si elles sont :
- indépendantes,
c'est-à-dire, pour tous réels , et, - de même loi,
c'est-à-dire pour tout .
où et sont les densités de probabilité respectives du couple et des variables et .
Une manière plus générale est de considérer les fonctions de répartition : les variables ont même loi si elles ont la même fonction de répartition et sont dites indépendantes[12] si pour tous réels où et sont les fonctions de répartition respectives du couple et des variables et . Cette définition se généralise pour variables aléatoires indépendantes, dites mutuellement indépendantes[8].
Plus mathématiquement, des variables iid sont supposées être définies sur le même espace[a 1], c'est-à-dire qu'il existe un espace probabilisé tel que chaque variable aléatoire est une fonction mesurable .
Définition générale — Des variables aléatoires réelles sont dites indépendantes et identiquement distribuées si elles sont :
- indépendantes, (ou mutuellement indépendantes[a 1])
c'est-à-dire pour toute sous-famille finie , pour tous réels , et - de même loi,
c'est-à-dire pour tout .
De manière plus générale, il est possible de considérer des variables aléatoires à valeurs non réelles, c'est-à-dire dans un espace mesurable général. Dans ce cas, chaque variable aléatoire est une fonction mesurable d'un espace probabilisé dans un espace mesurable. et . Ainsi, on dit que les variables et sont indépendantes et identiquement distribuées si :
- les événements et sont indépendants pour tous et ,
- les mesures images et de par et par sont égales.
Ces définitions se généralisent au cas d'une famille quelconque finie, dénombrable ou infinie non-dénombrable de variables aléatoires[13].
Propriétés[modifier | modifier le code]
Les variables iid apparaissent dans beaucoup de situations et résultats statistiques et probabilistes car elles possèdent de nombreuses propriétés qui permettent de mieux étudier leur loi de probabilité ou leur somme notamment. Dans la suite de cette section, sont des variables réelles indépendantes et identiquement distribuées.
Si on note la densité de probabilité du vecteur et la densité commune des variables , alors[12] : . Autrement dit, la fonction de densité d'un -uplet de variables iid est à variables séparables.
La somme de variables iid possède de bonnes propriétés ; donnons ici les principales. Si l'espérance commune des variables est et la variance commune est , alors la somme et la moyenne ont pour espérance et pour variance[14] :
- et ,
- et .
Si on note la fonction caractéristique commune des variables et celle de la somme , alors[14]
- .
La covariance et la corrélation de deux variables aléatoires indépendantes sont nulles : c'est-à-dire . Cependant une covariance nulle n'implique pas toujours l'indépendance des variables aléatoires[15]. Dans le cas où les variables sont les coordonnées d'un vecteur gaussien, leur indépendance est équivalente au fait que leurs covariances deux à deux soient nulles [16].
Si et sont iid, alors[17] : .
- Exemples de sommes de variables iid.
- Si sont iid de loi de Bernoulli de paramètre , alors[18] est de loi binomiale : .
- Si sont iid de loi géométrique de paramètre , alors[19] est de loi binomiale négative : .
- Si sont iid de loi de Poisson de paramètre , alors[20] est de loi de Poisson : .
- Si sont iid de loi exponentielle de paramètre , alors[21] est de loi Gamma : .
- Si sont iid de loi normale , alors[22] est de loi normale : .
- Si sont iid de loi normale de paramètre 0 et 1, alors[23] est de loi du χ² : .
- Si sont iid de loi du χ² de paramètre , alors[24] est de loi du χ² : .
Une généralisation de la notion de variables iid est celle de variables échangeables (en)[13] : les variables aléatoires réelles sont dites échangeables si la loi de probabilité du n-uplet est la même que la loi de pour toute permutation . Autrement dit, la loi du n-uplet ne dépend pas de l'ordre des variables.
Si des variables réelles sont indépendantes et identiquement distribuées, alors elles sont échangeables[13]. Il existe une réciproque partielle : des variables échangeables sont identiquement distribuées. Cependant, elles ne sont généralement pas indépendantes[25].
Le théorème central limite s'applique pour des variables iid, il existe des versions de ce théorème pour des variables échangeables[26].
En statistique[modifier | modifier le code]
La statistique est une science qui étudie et interprète les données. Lorsque l'on possède une série de données, la question se pose de savoir si elles peuvent être modélisées par des variables iid. Autrement dit : sont-elles des valeurs différentes obtenues de manière indépendante d'un même phénomène aléatoire[27] ? Les données peuvent être obtenues par mesures sur des individus ou objets qui doivent alors être choisis au hasard et avec remise[27]; elles peuvent également provenir d'une simulation grâce à un générateur de nombres aléatoires : dans ce cas la graine du générateur doit être choisie aléatoirement et ne doit plus être changée après[27].
Il y a plusieurs méthodes pour tester l'indépendance des variables : la visualisation du corrélogramme (ou graphique d'autocorrélation), la visualisation du graphe de retard (Lag-plot) ou la réalisation de tests statistiques.
Visualiser le graphique d’autocorrélation[modifier | modifier le code]

Dans le cas où la série est stationnaire, c'est-à-dire que les accroissements sont de covariance nulle, on peut s'intéresser à la fonction d'autocorrélation[28] (ACF). Elle est définie comme la corrélation entre la première valeur et la -ième valeur. Cette fonction permet d'évaluer si les données sont issues d'un modèle iid[28], elle est nulle si les données sont parfaitement iid[27].
Il est à noter que plus il y a de valeurs, plus la fonction d'autocorrélation est petite. En fait les valeurs de la fonction d'autocorrélation décroissent en fonction de la taille du nombre de données suivant le ratio .
Visualiser le graphe de retard[modifier | modifier le code]
Le graphique de retard (ou Lag-plot) est un nuage de points qui a pour abscisses les valeurs de la série de données et en ordonnées ces valeurs décalées de : en prenant l'indice modulo , c'est-à-dire en reprenant au début de la liste lorsque l'on arrive à la fin. Si un des nuages fait apparaître une tendance d'orientation, la série n'est pas considérée iid[29].
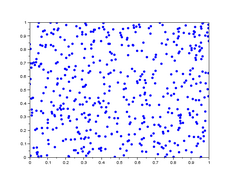
Dans la galerie d'images ci-dessous, sont représentés 5 lag-plot pour n=500 valeurs iid de loi uniforme simulées avec scilab. En abscisse : les 500 valeurs ; en ordonnées : les valeurs décalées de h . On remarque que les 5 graphiques n'ont pas de tendance d'orientation, ce qui est le cas de variables iid.
- Graphe de retard de valeurs iid
-
.
-
.
-
.
-
.
-
.
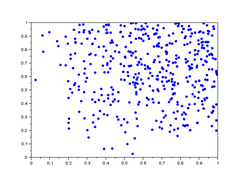
Dans la galerie d'images ci-dessous, sont représentés 5 lag-plot pour n=500 valeurs qui ne sont pas iid. Les valeurs sont construites comme le maximum de valeurs iid : et ne sont pas indépendantes car elles dépendent toutes deux de . On remarque une tendance du nuage de points vers le haut et la droite, notamment une concentration linéaire sur le premier graphique.
- Graphe de retard de valeurs non iid
-
.
-
.
-
.
-
.
-
.
Effectuer des tests statistiques[modifier | modifier le code]
Il est possible de réaliser des tests statistiques pour vérifier si les données sont associées à une loi de probabilité (tests d'adéquation) et d'autres pour vérifier si les données sont indépendantes (test d'indépendance). Il existe aussi des tests pour vérifier si des valeurs sont iid, comme le test du point tournant (en)[a 2],[30].
Si on note les valeurs obtenues, on dit que la suite de valeurs est monotone en si ou . Dans le cas contraire, on dit que est un point tournant. Intuitivement cela signifie que les valeurs ne sont pas ordonnées. Si les valeurs sont issues d'un modèle iid, alors le nombre de points tournants suit une loi normale lorsque tend vers . Il est alors possible de faire un test statistique : on teste contre .
Si est le nombre de points tournants pour valeurs, alors suit la loi . Si avec de loi normale centrée réduite, alors la valeur critique est :
- .
C'est-à-dire, si le nombre de points tournants est plus petit que , alors il est considéré comme trop petit et l'hypothèse iid est rejetée avec un risque de se tromper.
Par exemple, la série contient 2 points tournants pour valeurs. Pour un risque de , la table de valeur de la loi normale donne . Ainsi : . On rejette l'hypothèse et on conclut que les valeurs ne sont pas issues d'un modèle iid avec un risque de 5 % de se tromper. Cet exemple est réalisé avec une faible valeur de , ce qui ne le rend pas très performant.
Simulations[modifier | modifier le code]
Il est très utile de pouvoir simuler des valeurs issues de variables aléatoires identiquement distribuées. Lorsque l'on utilise une expérience aléatoire comme un lancer de dé, le résultat n'est en rien déterministe et on obtient alors des valeurs qui dépendent totalement du hasard. Cependant, il est compliqué d'automatiser des mécanismes physiques, on utilise alors des outils adaptés pour effectuer de grands nombres de calculs, comme l'ancienne méthode des tables de nombres aléatoires : la société RAND Corporation propose ainsi en 1955 une table d'un million de valeurs pseudo-aléatoires[a 3]. Le développement de l'informatique au XXe siècle a permis la création de générateurs de valeurs aléatoires. Le but est de simuler une liste de valeurs iid le mieux possible[a 4]. L'utilisation d'un algorithme déterministe, c'est-à-dire qui n'utilise pas d'expérience aléatoire, permet de simuler une liste de valeurs possédant presque les mêmes propriétés que des valeurs aléatoires. On parle dans ce cas de valeurs pseudo-aléatoires si elles sont[a 4],[31] :
- Non prévisibles : c'est-à-dire que la suite de valeurs ne peut pas être compressée, au sens où il est impossible de la décrire en utilisant moins de place que celle qu’elle occupe ;
- Équiréparties sur plusieurs entiers prédéfinis : c'est-à-dire que les fréquences d'apparition de chaque entier sont identiques.
Il n'est cependant pas possible d'obtenir un hasard indépendant parfait[a 4], c'est-à-dire équitablement réparties et ne dépendant pas les unes des autres. Deux problèmes se posent : obtenir des valeurs qui suivent la loi de probabilité recherchée et qui sont indépendantes entre elles. Il existe plusieurs méthodes pour simuler des valeurs iid, certaines sont plus rapides mais donnent des résultats moins probants, c'est-à-dire que l'équirépartition et l'imprévisibilité ne sont pas parfaites, on peut parler de hasard faible. D'autres méthodes utilisant des phénomènes physiques permettent d'obtenir de meilleurs résultats, on parle de hasard fort[a 4].
La plupart des générateurs de nombres aléatoires utilisent la loi uniforme continue pour générer d'autres lois de probabilité. Par exemple, si on considère une variable de loi uniforme, alors la variable définie par : si et si , est une variable aléatoire de loi de Bernoulli. Une manière plus générale est construite sur le résultat suivant :
- si est la fonction de répartition de la loi de probabilité recherchée et est une variable aléatoire de loi uniforme sur , alors est une variable aléatoire qui suit la loi de probabilité voulue[32],[33]. Ici est la transformée inverse[33].

Il reste alors à simuler une suite de valeurs de loi uniforme continue sur et indépendantes. Un des algorithmes classiques est basé sur les congruences de fonctions linéaires. Il permet de construire une suite de valeurs obtenues par itération[31] :
où :
- le module réalise la congruence, c'est-à-dire que toutes les valeurs seront dans l'ensemble ,
- le multiplicateur est la fonction linéaire,
- la valeur initiale est appelée la graine ou le germe.
Cet algorithme est chaotique dans le sens où un petit changement de la valeur initiale entraine des résultats différents[34]. Sous de bonnes conditions sur et , les valeurs de la suite sont considérées comme des réalisations de variables iid. Par exemple, et donnent de bons résultats ; la valeur de la graine peut être choisie aléatoirement en utilisant l'horloge interne de l'ordinateur par exemple. Les valeurs pseudo-aléatoires obtenues prennent les valeurs de manière équiprobable, ainsi en divisant par la grande valeur , on obtient des valeurs considérées uniformes sur [31].
Applications et exemples[modifier | modifier le code]
Exemple classique[modifier | modifier le code]
Un exemple de tirage iid est celui d'un jeu de pile ou face. Chaque lancer de la même pièce suit la même loi de Bernoulli de paramètre et est indépendant de ceux qui l'ont précédé ou vont lui succéder.
Dans cet exemple simple, le tirage pourrait ne plus être iid. On peut utiliser deux pièces différentes dont l'une n'est pas équilibrée comme l'autre. Par exemple une première pièce avec la probabilité d'obtenir pile et l'autre avec probabilité .
- si on utilise alternativement les deux pièces biaisées, les résultats ne suivent pas la même loi de probabilité, ils restent néanmoins indépendants ;
- si on lance systématiquement la pièce ayant le plus de chance de donner face après chaque tirage pile, les tirages ne sont plus indépendants car conditionnés par le résultat du tirage précédent. Les valeurs ne suivent pas non plus la même loi.
Théorèmes limites[modifier | modifier le code]
En théorie des probabilités et en statistique, il existe des théorèmes limites : c'est-à-dire une convergence lorsque le nombre de variables tend vers l'infini. Parmi les théorèmes limites les plus régulièrement étudiés figurent la loi des grands nombres et le théorème central limite[5]. Ces deux théorèmes s'appliquent dans le cas d'une répétition de fois la même expérience, c'est-à-dire dans le cas de variables indépendantes et identiquement distribuées. Voici leurs énoncés :
- Loi des grands nombres[35] : si sont des variables réelles indépendantes et identiquement distribuées d'espérance finie et de variance finie , alors la variable converge en probabilité vers .
- Théorème central limite[36] : si sont des variables réelles indépendantes et identiquement distribuées d'espérance finie et de variance finie , alors la variable convergent en loi vers une variable aléatoire de loi normale centrée réduite.
L'hypothèse iid de ces théorèmes est suffisante mais n'est pas nécessaire. Par exemple, la loi des grands nombres s'applique également lorsque la covariance des variables converge vers 0 lorsque la distance entre les indices grandit[37] : avec .
Au XXe siècle, Benoît Mandelbrot désigne différents types de hasard[38] : ceux dits « bénins » qui vérifient les hypothèses des théorèmes limites précédents et ceux plus « sauvages » ou « chaotiques » qui ne vérifient pas l'hypothèse iid. Autrement dit, ces deux théorèmes permettent en un certain sens de classifier des types de hasard.
Processus et bruit blanc[modifier | modifier le code]
Un processus stochastique représente l'évolution en fonction du temps d'une variable aléatoire. Il est alors prenant de s'intéresser aux accroissements des processus.
Pour un processus stochastique , si pour toutes variables , les accroissements sont indépendants, alors le processus est dit à accroissements indépendants[39]. De plus, si la loi de probabilité des accroissements , pour tout ne dépend pas de , alors le processus est dit stationnaire[39].
Il existe de nombreux cas de processus stationnaires à accroissements indépendants : la marche aléatoire dans le cas où la variable de temps est un nombre entier, le processus de Wiener ou mouvement brownien dans le cas où suit une loi normale , le processus de Poisson et plus généralement les processus de Markov, le processus de Lévy.
Un autre exemple de processus à accroissements indépendants et stationnaires est le bruit blanc. C'est un processus stochastique tel que[39] : pour tous et ,
- , l'espérance est constante ;
- , la variance est constante ;
- , la covariance est nulle.
On dit que c'est un processus iid car il est formé de variables indépendantes et identiquement distribuées[39]. Si de plus la loi de est normale alors le bruit blanc est parfois dit « gaussien » et est noté nid (normal et identiquement distribué).
Méthode de Monte-Carlo[modifier | modifier le code]
Les méthodes de Monte-Carlo permettent d'estimer numériquement des résultats grâce à l'usage de valeurs aléatoires ; elles servent à éviter les calculs exacts[40] (elles ont l'avantage de réduire le temps de calculs ou encore d'approximer un résultat dont le calcul exact est impossible à réaliser). Plus précisément, la méthode de Monte-Carlo ordinaire utilise des variables indépendantes et identiquement distribuées . Grâce au théorème central limite, la variable aléatoire converge en loi vers une variable aléatoire de loi normale[41]. Grâce à la connaissance de la loi normale, on peut donc obtenir une valeur approchée de la valeur recherchée pour un grand nombre de variables aléatoires considérées. Ainsi la moyenne empirique est une valeur approchée de la vraie moyenne recherchée. Plus précisément[41], on peut obtenir un intervalle de confiance de la moyenne au seuil de confiance 95 % :
- où .
Cette méthode sert également à réaliser d'autres types de calculs, tel que le calcul d'intégrale, ou permet également de donner une méthode pour simuler différentes variables d'une loi prédéfinie, en utilisant par exemple l'algorithme de Metropolis-Hastings ou l'échantillonnage de Gibbs[40].
La méthode de Monte-Carlo existe aussi dans le cas où les variables ne sont plus iid, on parle alors de méthode de Monte-Carlo par chaînes de Markov. La suite de variables aléatoires est alors une chaîne de Markov stationnaire. La perte de l'hypothèse iid complique les résultats[42].
Notes et références[modifier | modifier le code]
- Henry 2001, p. 20.
- Henry 2001, p. 23.
- Henry 2001, p. 29.
- Henry 2001, p. 142.
- Henry 2001, p. 127.
- Henry 2001, p. 122.
- Lejeune 2004, p. 39.
- Lejeune 2004, p. 37.
- Le Boudec 2015, p. 39.
- Morgenthaler 2007, p. 100.
- Morgenthaler 2007, p. 85.
- Morgenthaler 2007, p. 86.
- Severini 2005, p. 59.
- Lejeune 2004, p. 38.
- Lejeune 2004, p. 36.
- Lejeune 2004, p. 42.
- Lejeune 2004, p. 43.
- Lejeune 2004, p. 48.
- Lejeune 2004, p. 50.
- Lejeune 2004, p. 53.
- Lejeune 2004, p. 56.
- Lejeune 2004, p. 57.
- Lejeune 2004, p. 72.
- Lejeune 2004, p. 73.
- Severini 2005, p. 60.
- Severini 2005, p. 399.
- Le Boudec 2015, p. 40.
- Le Boudec 2015, p. 143.
- Le Boudec 2015, p. 41.
- Le Boudec 2015, p. 123.
- Bogaert 2005, p. 242.
- Bogaert 2005, p. 244.
- Le Boudec 2015, p. 179.
- Le Boudec 2015, p. 175.
- Severini 2005, p. 342.
- Severini 2005, p. 365.
- Severini 2005, p. 344.
- Henry 2001, p. 129.
- Bourbonnais et Terraza 2010, p. 85.
- Brooks et al. 2011, p. 3.
- Brooks et al. 2011, p. 7.
- Brooks et al. 2011, p. 8.
- Articles et autres sources
- (en) « Sequence of random variables and their convergence », sur Statlect.
- (en) Vicky Yang, « turning.point.test », sur inside-R.
- (en) « A Million Random Digits with 100,000 Normal Deviates », sur Rand Corporation.
- Jean-Paul Delahaye, « Aléa du hasard informatique », Pour la science, no 245, , p. 92-97 (lire en ligne).
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- Patrick Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, De Boeck Supérieur, , 402 p. (ISBN 2-8041-4794-0, lire en ligne)

- Régis Bourbonnais et Michel Terraza, Analyse des séries temporelles, Dunod, , 352 p. (ISBN 978-2-10-056111-7, lire en ligne)

- (en) Steve Brooks, Andrew Gelman, Galin Jones et Xiao-Li Meng, Handbook of Markov Chain Monte Carlo, CRC Press, , 619 p. (ISBN 978-1-4200-7942-5, lire en ligne)

- Michel Henry, Autour de la modélisation en probabilités, Presses Univ. Franche-Comté, , 258 p. (ISBN 2-84627-018-X, lire en ligne)

- (en) Jean-Yves Le Boudec, Performance Evaluation of Computer and Communication Systems, EPFL, , 359 p. (lire en ligne [PDF])
- Michel Lejeune, Statistique : la théorie et ses applications, Paris/Berlin/Heidelberg etc., Springer Science & Business Media, , 339 p. (ISBN 2-287-21241-8, lire en ligne)

- Stephan Morgenthaler, Introduction à la statistique, Presse polytechniques, , 387 p. (ISBN 978-1-4710-3427-5, lire en ligne)

- (en) Thomas A. Severini, Elements of Distribution Theory, Cambridge University Press, , 515 p. (ISBN 978-0-521-84472-7, lire en ligne)



































































































![{\displaystyle H_{0}=[x_{1},x_{2},\dots ,x_{n}{\text{ sont }}iid.]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972a1aec11006dc66b522a59cd0a2d35998be6c9)
![{\displaystyle H_{1}=[x_{1},x_{2},\dots ,x_{n}{\text{ ne sont pas }}iid.]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efeed4e1c7636b2b04e02b1abca7382480eb68a3)



















![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
































![{\displaystyle [{\hat {\mu }}_{n}-1,96{\frac {{\hat {\sigma }}_{n}}{\sqrt {n}}}\,;\,{\hat {\mu }}_{n}+1,96{\frac {{\hat {\sigma }}_{n}}{\sqrt {n}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39cf8f610348f859d160f661d698c250beb168b)
