Loi de Poisson
| Loi de Poisson | |
 Fonction de masse Les fonctions de masse ne sont définies que pour les entiers k. | |
 Fonction de répartition Les fonctions de répartition sont discontinues en chaque entier naturel. | |
| Paramètres | [1] |
|---|---|
| Support | |
| Fonction de masse | |
| Fonction de répartition |
(où est la Fonction gamma incomplète) et où est la partie entière par défaut de x |
| Espérance | |
| Médiane | |
| Mode | si est un réel non entier,
et si est un nombre entier |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Entropie |
Pour grand :
|
| Fonction génératrice des moments | |
| Fonction caractéristique | |
| Fonction génératrice des probabilités | |
| modifier |
|
En théorie des probabilités et en statistiques, la loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre d'événements se produisant dans un intervalle de temps fixé, si ces événements se produisent avec une fréquence moyenne ou espérance connue, et indépendamment du temps écoulé depuis l'événement précédent.
La loi de Poisson est également pertinente pour décrire le nombre d'événements dans d'autres types d'intervalles, spatiaux plutôt que temporels, comme des segments, surfaces ou volumes.
Histoire[modifier | modifier le code]

La loi de Poisson a été introduite en 1838 par Denis Poisson (1781–1840), dans son ouvrage Recherches sur la probabilité des jugements en matière criminelle et en matière civile[2]. Le sujet principal de cet ouvrage consiste en certaines variables aléatoires qui dénombrent, entre autres choses, le nombre d'occurrences (parfois appelées « arrivées ») qui prennent place pendant un laps de temps donné.
Définition[modifier | modifier le code]
Si le nombre moyen d'occurrences dans un intervalle de temps fixé est λ, alors la probabilité qu'il existe exactement k occurrences (k étant un entier naturel, k = 0, 1, 2…) est où :
- e est la base de l'exponentielle (e ≈ 2,718...) ;
- k! est la factorielle de k. Il correspond à la valeur étudiée ;
- λ est un nombre réel strictement positif[1]. Il correspond à la moyenne théorique de l'échantillon.
On dit alors que X suit la loi de Poisson de paramètre λ, noté .
Par exemple, si un certain type d'événements se produit en moyenne 4 fois par minute, pour étudier le nombre d'événements se produisant dans un laps de temps de 10 minutes, on choisit comme modèle une loi de Poisson de paramètre λ = 10×4 = 40.
Calcul de p(k)[modifier | modifier le code]
Ce calcul peut se faire de manière déductive en travaillant sur une loi binomiale de paramètres . Pour T grand, on démontre que la loi binomiale converge vers la loi de Poisson.
Il peut aussi se faire de manière inductive en étudiant sur l'intervalle [0 ; T] les fonctions Fk(t), qui donnent la probabilité que l'événement se produise k fois sur l'intervalle de temps [0 ; t]. En utilisant la récurrence et du calcul différentiel, on parvient à retrouver les formules précédentes[3].
Propriétés[modifier | modifier le code]
Dans toute cette section X est une variable aléatoire suivant une loi de Poisson de paramètre λ.
Moments et fonctions génératrices[modifier | modifier le code]
Moments ordinaires[modifier | modifier le code]
Les quatre premiers moments ordinaires d'une loi de Poisson sont donnés par[4] :
On en déduit la variance et l'écart type :
Plus généralement, le n-ième moment ordinaire d'une loi de Poisson de paramètre λ estoù S(n, k) est le nombre de Stirling de seconde espèce de paramètres n et k.
En particulier lorsque λ = 1, le n-ième moment de X correspond au n-ième nombre de Bell. En effet cela est une conséquence de la formule de Dobiński.
La borne suivante majore les moments d'une loi de Poisson[5] : On a la relation de récurrence[6] :
Moments centrés[modifier | modifier le code]
Les quatre premiers moments centrés d'une loi de Poisson sont donnés par[4],[6] :
On en déduit l'asymétrie et le kurtosis normalisé :
On a la relation de récurrence[6] :
Moments factoriels[modifier | modifier le code]
Le r-ième moment factoriel d'une loi de Poisson est
où désigne la factorielle décroissante.
Fonction génératrice des probabilités[modifier | modifier le code]
La fonction génératrice des probabilités d'une loi de Poisson est
Fonction génératrice des moments[modifier | modifier le code]
La fonction génératrice des moments d'une loi de Poisson est
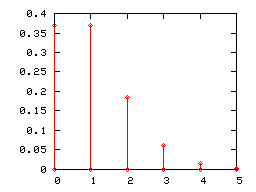
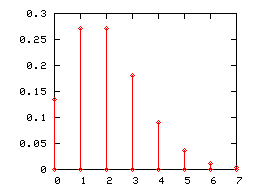
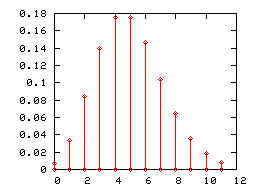
Diagramme en bâton[modifier | modifier le code]
Comme toute loi de probabilité discrète, une loi de Poisson peut être représentée par un diagramme en bâtons. Ci-dessous sont représentés les diagrammes en bâtons des lois de Poisson de paramètres 1, 2 et 5.
Lorsque le paramètre λ de la loi de Poisson devient grand, (pratiquement lorsqu'il est supérieur à 5), son diagramme en bâton est correctement approché par l'histogramme d'une loi normale d'espérance et de variance égales à λ (l'intervalle de classe étant égal à l'unité). Cette convergence était mise à profit, avant que les moyens informatiques ne se généralisent, pour utiliser la loi normale en lieu et place de la loi de Poisson dans certains tests.
Stabilité de la loi de Poisson par la somme[modifier | modifier le code]
Si les variables {Xi}i=1,...,n sont indépendantes et suivent une loi de Poisson de paramètres respectifs λi, alors leur somme suit une loi de Poisson de paramètre la somme des λi:
Bornes de queue[modifier | modifier le code]
Un argument de type borne de Chernoff permet de déduire les bornes de queue suivantes[7]
- pour tout x > λ et
- pour tout x < λ.
Ces bornes peuvent se réécrire de la manière suivante[8]
- pour tout x > 0 et
- pour tout λ > x > 0
où pour tout . Ces dernières bornes impliquent en particulier la borne suivante[8] (qui est plus faible mais plus agréable à manipuler)
- .
La borne supérieure donnée par Chernoff peut être améliorée d'un facteur 2 au moins[9]
- pour tout x > 0.
Il est à noter que la fonction h est liée à la divergence de Kullback-Leibler entre une loi de Poisson de paramètre x + λ et une loi de Poisson de paramètre λ. En effet on a la relation
- .
Simulation[modifier | modifier le code]
Un algorithme simple pour simuler la loi de Poisson consiste à utiliser le résultat suivant :
Théorème — Soit (Ei)i ≥ 1 une suite de variables aléatoires indépendantes et de même loi exponentielle de paramètre λ. On pose S1 = E1 et pour n ≥ 2, Sn = E1 + ... + En. On a alors :
La méthode de la transformée inverse permet de donner une façon simple de générer un tirage aléatoire suivant une loi exponentielle :
- Si U suit une loi uniforme sur [0 ; 1], alors E = –1λln(U) suit une loi exponentielle de paramètre λ.
En générant les par l'intermédiaire de variables aléatoires , On a ainsi et, en notant :
L'algorithme peut ainsi se simplifier en :
- k ← 0, p ← 1
- tant que p > e–λ
- on tire u selon un tirage aléatoire uniforme sur [0 ; 1]
- p ← p×u
- k ← k+1
- on renvoie k – 1
Estimation du paramètre λ[modifier | modifier le code]
L'estimateur par maximum de vraisemblance du paramètre λ d'un échantillon issu d'une loi de Poisson est la moyenne empirique. C'est un estimateur convergent, sans biais, efficace, complet (en), exhaustif.
Lien avec d'autres lois de probabilités[modifier | modifier le code]
- Si X et Y sont deux variables aléatoires indépendantes qui suivent des lois de Poisson de paramètres respectifs λ et μ, alors X – Y est une variable aléatoire qui suit une loi de Skellam de paramètres (λ,μ).
- Si X et Y sont deux variables aléatoires indépendantes qui suivent des lois de Poisson de paramètres λ et μ, alors la loi conditionnelle de X sachant X + Y est une loi binomiale.
- Pour de grandes valeurs de λ, on peut approcher la loi de Poisson par la loi normale de moyenne λ et de variance λ.
Lien avec la loi de Bernoulli[modifier | modifier le code]
Le décompte des événements rares se fait souvent au travers d'une somme de variables de Bernoulli, la rareté des événements se traduisant par le fait que les paramètres de ces variables de Bernoulli sont petits (ainsi, la probabilité que chaque événement survienne est faible). Le lien entre la loi de Poisson et les événements rares peut alors s'énoncer ainsi :
Paradigme de Poisson — La somme Sn d'un grand nombre de variables de Bernoulli indépendantes de petit paramètre suit approximativement la loi de Poisson de paramètre
L'inégalité de Le Cam précise le paradigme de Poisson : soit un tableau de variables aléatoires de Bernoulli indépendantes, avec paramètres respectifs pk,n. On note
En particulier, si les deux conditions suivantes sont réunies :
alors Sn converge en loi vers la loi de Poisson de paramètre λ.
Dans l'énoncé du paradigme de Poisson, on fait deux hypothèses (vagues) sur les termes d'une somme Sn de variables de Bernoulli :
- les paramètres des variables de Bernoulli sont petits ; or les deux conditions ci-dessus entraînent que
ce qui reformule l'hypothèse « les paramètres des variables de Bernoulli sont petits » de manière plus précise ;
- il y a un grand nombre de termes ; or les deux conditions ci-dessus entrainent que le nombre de termes tend vers l'infini :
- Ce paradigme reste pertinent, dans certaines conditions, si l'on relaxe l'hypothèse d'indépendance[11].
- Un exemple frappant est le nombre de points fixes d'une permutation tirée au hasard.
- Un autre exemple est le nombre de points isolés du graphe aléatoire, dont la convergence vers la loi de Poisson a permis à Erdös et Rényi de démontrer, en 1960, le théorème double-exponentiel.
- Le cas particulier an=n, pk,n=λ/n, λn=λ, de l'inégalité de Le Cam, précise la rapidité de convergence de la loi binomiale de paramètres n et λ/n vers la loi de Poisson de paramètre λ.
Domaines d'application[modifier | modifier le code]
Le domaine d'application de la loi de Poisson a été longtemps limité à celui des événements rares comme les suicides d'enfants, les arrivées de bateaux dans un port ou les accidents dus aux coups de pied de cheval dans les armées (étude de Ladislaus Bortkiewicz[12]).
Mais, depuis la fin du XXe siècle, son champ d'application s'est considérablement élargi. On l'utilise beaucoup dans les télécommunications (pour compter le nombre de communications dans un intervalle de temps donné), le contrôle de qualité statistique (nombre de défauts en SPC), la description de certains phénomènes liés à la désintégration radioactive (la désintégration des noyaux radioactifs suivant, par ailleurs, une loi exponentielle de paramètre noté aussi lambda), la biologie (mutations dans l'expérience de Luria et Delbrück, nombre de potentiels d'actions émis par un neurone en neurosciences), la météorologie, la finance pour modéliser la probabilité de défaut d'un crédit, le Yield Management (American Airlines, Lufthansa et SAS pour estimer la demande de passagers), etc.
La loi de Poisson est également utilisable dans le cadre sportif. Elle peut être utilisée afin d'effectuer des prédictions statistiques sur le nombre de buts inscrits lors d'un match. Les probabilités issues de ce modèle permettent aux bookmakers de définir leurs cotes.
En littérature[modifier | modifier le code]
Dans le roman de Thomas Pynchon, L'Arc-en-ciel de la gravité, un des personnages, le statisticien Roger Mexico, utilise la loi de Poisson pour cartographier les zones d'impact des fusées allemandes V2 sur la ville de Londres durant la Seconde Guerre mondiale.
Notes et références[modifier | modifier le code]
- Avec les conventions habituelles 0! = 1 et 00 = 1, la définition de la loi de Poisson s'étend à λ = 0 : on trouve alors p(0) = 1 et, dès que k > 0, p(k) = 0. Ainsi une variable aléatoire nulle presque sûrement peut être vue comme suivant la loi de Poisson de paramètre 0. Cette convention est cohérente avec les propriétés essentielles de la loi de Poisson de paramètre strictement positif. Elle est commode, voire indispensable, par exemple lors de l'étude des processus ponctuels de Poisson.
- Siméon-Denis Poisson, Recherches sur la probabilité des jugements en matière criminelle et en matière civile ; précédées des Règles générales du calcul des probabilités sur Gallica, 1837, passage 81, p. 205.
- Voir par exemple, Michel Henry, Autour de la modélisation en probabilités, Presses universitaires de Franche-Comté, (présentation en ligne), p. 229-231 ou encore ces notes de cours.
- (en) Eric W Weisstein, « Poisson Distribution », sur mathworld.wolfram.com
- (en) D Ahle Thomas, « Sharp and Simple Bounds for the raw Moments of the Binomial and Poisson Distributions », arXiv, (arXiv 2103.17027, lire en ligne)
- (en) Norman L Johnson, Adrienne W Kemp et Samuel Kotz, Univariate Discrete Distributions, Wiley, , 3e éd. (ISBN 978-0-471-27246-5, lire en ligne), p. 162
- (en) Michael Mitzenmacher et Eli Upfal, Probability and Computing: Randomized Algorithms and Probabilistic Analysis, Cambridge UK, Cambridge University Press, (ISBN 978-0-521-83540-4, lire en ligne), p. 97
- (en) « A short note on Poisson tail bounds »
- (en) Michael Short, « Improved Inequalities for the Poisson and Binomial Distribution and Upper Tail Quantile Functions », International Scholarly Research Notices, vol. 2013, (DOI https://doi.org/10.1155/2013/412958, lire en ligne)
- (en) L. Le Cam, « An Approximation Theorem for the Poisson Binomial Distribution », Pacific Journal of Mathematics, vol. 10, no 4, , p. 1181–1197 (lire en ligne, consulté le ).
- (en) A. D. Barbour, L. Holst et S. Janson, Poisson approximation, Oxford, The Clarendon Press Oxford University Press, , 277 p. (ISBN 0-19-852235-5).
- Ladislaus Bortkiewicz, Das Gesetz der kleinen Zahlen, (lire en ligne), p. 23.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Probabilité
- Probabilité (mathématiques élémentaires)
- Loi de probabilité
- Loi de Bernoulli
- Données de comptage
Lien externe[modifier | modifier le code]
- Arthur Charpentier, « La loi des petits nombres », sur Freakonometrics,

![{\displaystyle \lambda \in {}]0,+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d64752215a3200cc640a035056f6d840f009fe0b)












![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!\mathrm {e} ^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/787e3b96d4cd5fce046e601ffe6def105be10f81)







![{\displaystyle {\begin{array}{lll}\mathbb {E} [X]&=&\lambda \\\mathbb {E} [X^{2}]&=&\lambda (1+\lambda )\\\mathbb {E} [X^{3}]&=&\lambda (1+3\lambda +\lambda ^{2})\\\mathbb {E} [X^{4}]&=&\lambda (1+7\lambda +6\lambda ^{2}+\lambda ^{3})\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b5f229e400d5527be88286de93808928fee3fd0)


![{\displaystyle \mathbb {E} [X^{k}]\leq \left[{\frac {k}{\ln \left(k/\lambda +1\right)}}\right]^{k}\leq \lambda ^{k}\mathrm {e} ^{\frac {k^{2}}{2\lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0265dc6113c82a0118e997e1de9c07972ad39ab)
![{\displaystyle \mathbb {E} [X^{n}]=\lambda \mathbb {E} [X^{n-1}]+\lambda {\frac {\partial \mathbb {E} [X^{n-1}]}{\partial \lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9be13f332e8e03361fd2d757d4e7418692915d)
![{\displaystyle {\begin{array}{lll}\mathbb {E} [(X-\lambda )^{2}]&=&\lambda \\\mathbb {E} [(X-\lambda )^{3}]&=&\lambda \\\mathbb {E} [(X-\lambda )^{4}]&=&\lambda (1+3\lambda )\\\mathbb {E} [(X-\lambda )^{5}]&=&\lambda (1+10\lambda )\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca8e9b593d346b6915a7b04e1d6b473eea1b6c7b)

![{\displaystyle \mathbb {E} [(X-\lambda )^{n+1}]=n\lambda \mathbb {E} [(X-\lambda )^{n-1}]+\lambda {\frac {\partial \mathbb {E} [(X-\lambda )^{n}]}{\partial \lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/955a8a1c478f4348faa633d0b0bc3ce5781744c4)






![{\displaystyle {\begin{aligned}V(X)&=\mathbb {E} (X^{2})-(\mathbb {E} (X))^{2}&\\&=\sum _{k=1}^{\infty }k^{2}\,\mathbb {P} (X=k)-\lambda ^{2}&\\&=\sum _{k=1}^{\infty }k^{2}\,\mathrm {e} ^{-\lambda }{\frac {\lambda ^{k}}{k!}}-\lambda ^{2}&\\&=\lambda \,\mathrm {e} ^{-\lambda }\sum _{k=1}^{\infty }\,{\frac {k\lambda ^{k-1}}{(k-1)!}}-\lambda ^{2}&\\&=\lambda \,\mathrm {e} ^{-\lambda }\sum _{k=1}^{\infty }\,{\frac {d}{d\lambda }}{\frac {\lambda ^{k}}{(k-1)!}}-\lambda ^{2}&\qquad ({\text{la série entière ayant un rayon de convergence infini,}}\\&=\lambda \,\mathrm {e} ^{-\lambda }{\frac {d}{d\lambda }}\sum _{k=1}^{\infty }\,{\frac {\lambda ^{k}}{(k-1)!}}-\lambda ^{2}&\qquad {\text{on peut inverser la sommation et la dérivation}})\\&=\lambda \,\mathrm {e} ^{-\lambda }{\frac {d}{d\lambda }}\left[\lambda \sum _{k=1}^{\infty }\,{\frac {\lambda ^{k-1}}{(k-1)!}}\right]-\lambda ^{2}&\qquad ({\text{on reconnaît le développement en série entière de }}\mathrm {e} ^{\lambda })\\&=\lambda \,\mathrm {e} ^{-\lambda }{\frac {d}{d\lambda }}[\lambda \,\mathrm {e} ^{\lambda }]-\lambda ^{2}&\\&=\lambda \,\mathrm {e} ^{-\lambda }(\lambda +1)\,\mathrm {e} ^{\lambda }-\lambda ^{2}&\\&=\lambda \,(\lambda +1)-\lambda ^{2}&\\&=\lambda .&\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b8c275017a53b44357fe83f517049c0073b4052)




















![{\displaystyle U_{i}\sim {\mathcal {U}}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fce1e9d33243e1fdcd927a54142576a7b7b61df1)



![{\displaystyle \mathbb {E} [S_{n}].\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4169e81cf9921bebbec6592d094a01e875df7b5a)

![{\displaystyle S_{n}=\sum _{k=1}^{a_{n}}\,X_{k,n}\quad {\text{et}}\quad \lambda _{n}\ =\ \mathbb {E} [S_{n}]=\sum _{k=1}^{a_{n}}\,p_{k,n}.\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa48961dc784a0fd1d047e71159fdd008492bea8)




