Loi de Rayleigh

Loi de Rayleigh
Densité de probabilité
Fonction de répartition
Paramètres	$\sigma >0\,\,$ (nombre réel)
Support	$x\in [0;\infty [$
Densité de probabilité	${\frac {x\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}{\sigma ^{2}}}$
Fonction de répartition	$1-\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)$
Espérance	$\sigma {\sqrt {\frac {\pi }{2}}}$
Médiane	$\sigma {\sqrt {\ln(4)}}\,$
Mode	$\sigma \,$
Variance	${\frac {4-\pi }{2}}\sigma ^{2}$
Asymétrie	${\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}$
Kurtosis normalisé	$-2{\frac {3\pi ^{2}-12\pi +8}{(4-\pi )^{2}}}$
Entropie	$1+\ln \left({\frac {\sigma }{\sqrt {2}}}\right)+{\frac {\gamma }{2}}$
Fonction génératrice des moments	$1+\sigma t\,\mathrm {e} ^{\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\left({\textrm {erf}}\left({\frac {\sigma t}{\sqrt {2}}}\right)\!+\!1\right)$
Fonction caractéristique	$1\!-\!\sigma t\mathrm {e} ^{-\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\!\left({\textrm {erfi}}\!\left({\frac {\sigma t}{\sqrt {2}}}\right)\!-\!i\right)$

En probabilités et en statistiques, la loi de Rayleigh, est une loi de probabilité à densité. Elle apparaît comme la norme d'un vecteur gaussien bi-dimensionnel dont les coordonnées sont indépendantes, centrées et de même variance. Cette loi de probabilité est baptisée d'après Lord Rayleigh. Typiquement, la distance D_n à laquelle une particule se trouve de son point de départ, après avoir effectué n pas d'une marche aléatoire symétrique dans le plan, suit approximativement une loi de Rayleigh de paramètre √n. Dans un tout autre domaine, elle est fréquemment utilisée pour décrire l'enveloppe d'un processus de Gauss à bande étroite.

Définition

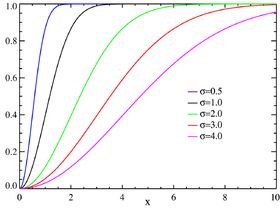
La loi de Rayleigh est la loi de probabilité de densité :

$f(x;\sigma ^{2})={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)$

pour $x\in [0,\infty [.$

Propriétés

Les moments sont donnés par :

$m_{k}=\sigma ^{k}2^{k/2}\,\Gamma (1+k/2)\,$

où Γ(z) est la fonction Gamma.

L'espérance et la variance d'une variable aléatoire de Rayleigh X sont les suivantes :

$\mathbb {E} [X]=\sigma {\sqrt {\frac {\pi }{2}}}\approx 1{,}253\cdot \sigma \,$

et

${\textrm {Var}}(X)={\frac {4-\pi }{2}}\sigma ^{2}\approx 0{,}429\cdot \sigma ^{2}\,.$

Le coefficient d'asymétrie ((en) skewness) est :

$\gamma _{1}={\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}\approx 0{,}631.$

La kurtosis est :

$\gamma _{2}=-{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}\approx 0{,}245.$

La fonction caractéristique est :

$\varphi (t):1\!-\!\sigma t\mathrm {e} ^{-\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\!\left({\textrm {erfi}}\!\left({\frac {\sigma t}{\sqrt {2}}}\right)\!-\!i\right)$

où erfi(z) est la fonction d'erreur complexe. La transformée de Laplace est

$M(t)=\,1+\sigma t\,\mathrm {e} ^{\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\left({\textrm {erf}}\left({\frac {\sigma t}{\sqrt {2}}}\right)\!+\!1\right),$

où erf(z) est la fonction d'erreur.

Entropie

L'entropie est

$H=1+\ln \left({\frac {\sigma }{\sqrt {2}}}\right)+{\frac {\gamma }{2}}\approx 1{,}2886+\ln \left(0{,}707\cdot \sigma \right)$

où γ est la constante d'Euler-Mascheroni.

Estimation du paramètre

Étant donné N variables de Rayleigh indépendantes et de même loi de paramètre σ, l'estimateur du maximum de vraisemblance de σ est

${\hat {\sigma }}={\sqrt {{\frac {1}{2N}}\sum _{i=1}^{N}X_{i}^{2}}}.$

Engendrer des variables de Rayleigh

Étant donné une variable U uniforme sur l'intervalle ]0;1[, la variable

$X=\sigma {\sqrt {-2\ln(U)}}\,$

suit la loi de Rayleigh de paramètre σ. Cela provient de la forme de la fonction de répartition, en particulier du théorème de la réciproque, et du fait que 1–U a même loi que U.

Lien avec d'autres lois continues

• $R\sim \mathrm {Rayleigh} (\sigma )$ suit la loi de Rayleigh si $R={\sqrt {X^{2}+Y^{2}}}$, où $X\sim {\mathcal {N}}(0,\sigma ^{2})$ et $Y\sim {\mathcal {N}}(0,\sigma ^{2})$ sont deux variables gaussiennes indépendantes, ce qui explique le choix du symbole "σ" pour paramétriser la loi de Rayleigh.
• Si $R\sim \mathrm {Rayleigh} (1)$, alors R² suit la loi du χ² avec deux degrés de liberté: $R^{2}\sim \chi _{2}^{2},\$ qui est une loi exponentielle de paramètre 1/2.
• Si X suit une loi exponentielle $X\sim {\mathcal {E}}(\lambda )$, alors $Y={\sqrt {2X\sigma ^{2}\lambda }}\sim \mathrm {Rayleigh} (\sigma )$.
• Si $R_{i}\sim \mathrm {Rayleigh} (\sigma )$, et si les R_i forment une suite de variables indépendantes, alors $\sum _{i=1}^{N}R_{i}^{2}$ suit une loi gamma de paramètres N et 2σ² : $\left[Y=\sum _{i=1}^{N}R_{i}^{2}\right]\sim \Gamma \left(N,2\sigma ^{2}\right)$.
• La loi de Rice est une généralisation de la loi de Rayleigh.

Lien avec certaines lois discrètes

Marche aléatoire dans le plan

Trois réalisations de marches aléatoires isotropes sur le réseau ${\textstyle \mathbb {Z} ^{2}\ }$ (en 10 000 pas). La distance maximale (ou, aussi bien, la distance terminale) sont typiquement de l'ordre de 100 pas.

Notons D_n la distance entre la position d'un marcheur au hasard dans le plan, après n pas au hasard, et son point de départ : D_n/√n converge en loi vers la loi de Rayleigh, ce qui signifie qu'en parcourant une distance n, le marcheur ne s'éloigne vraiment de son point de départ que de √n pas approximativement, la convergence vers la loi de Rayleigh permettant de préciser cette approximation.

Distance entre deux points au hasard d'un arbre de Cayley aléatoire

À l'aide de la bijection de Joyal, on peut montrer que la loi de la distance D_n entre deux points au hasard d'un arbre de Cayley aléatoire est donnée, pour $0\ \leq \ k\ \leq \ n-1,\$ par

$\mathbb {P} (D_{n}=k)\ =\ {\frac {(k+1)\times (n)_{\downarrow k+1}}{n^{k+2}}}.$

On peut montrer, par exemple à l'aide du lemme de Scheffé, que D_n/√n converge en loi vers la loi de Rayleigh, ce qui indique que la distance "typique" entre deux points d'un arbre de taille n est de l'ordre de √n.

Points cycliques d'une application

En vertu de la bijection de Joyal, le nombre $C_{n}(\omega )\$ de points cycliques d'une application ω de $[\![1,n]\!]$ dans $[\![1,n]\!]$, suit la même loi que D_n. Ainsi, C_n/√n converge en loi vers la loi de Rayleigh.

Problème des anniversaires

Cette loi discrète apparaît aussi dans des problèmes d'allocations (boules et urnes), dont le fameux paradoxe des anniversaires. Lorsqu'on alloue séquentiellement des boules dans un ensemble de n urnes, avec équiprobabilité, ce qui revient à considérer un univers probabiliste $\Omega \ =\ [\![1,n]\!]^{\mathbb {N} },\$ le rang $T_{n}(\omega )\$ de la première boule à être allouée dans une urne non vide suit la même loi que 2 + D_n Ainsi, T_n/√n converge en loi vers la loi de Rayleigh.

Pour n=365, soit 365 boîtes, $T_{n}(\omega )\$ s'interprète comme la taille du groupe pour laquelle il devient probable qu'au moins deux membres du groupe ait la même date d'anniversaire (il faut imaginer un groupe dont l'effectif augmente progressivement) : la probabilité que dans un groupe de $\alpha {\sqrt {n}}\$ personnes, toutes les dates d'anniversaire soit différentes, est approximativement

$\mathrm {e} ^{-\alpha ^{2}/2}\ =\ \int _{\alpha }^{+\infty }\,f(x;1)\,\mathrm {d} x,$

et vaut donc 1/2 pour un groupe d'approximativement ${\sqrt {365\times 2\ln(2)}}\$ (soit 22,5) personnes, ou bien 1/10 pour un groupe d'approximativement ${\sqrt {365\times 2\ln(10)}}\$ (soit 41) personnes. Le calcul exact du premier entier tel que cette probabilité soit plus petite que 1/2 (respectivement 1/10) donne les mêmes résultats : 23 (respectivement 41).