Distribution de Lévy
Densité de probabilité pour différentes valeurs de c.
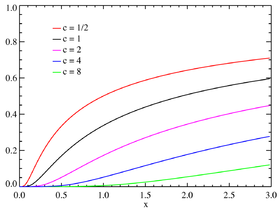
Fonction de répartition pour différentes valeurs de c.
Paramètres
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
c
>
0
{\displaystyle c>0\,}
Support
x
∈
]
μ
,
+
∞
[
{\displaystyle x\in ]\mu ,+\infty [\,}
Densité de probabilité
c
2
π
⋅
1
(
x
−
μ
)
3
/
2
e
−
c
2
(
x
−
μ
)
{\displaystyle {\sqrt {\frac {c}{2\pi }}}\cdot {\frac {1}{(x-\mu )^{3/2}}}\mathrm {e} ^{-{\frac {c}{2(x-\mu )}}}}
Fonction de répartition
e
r
f
c
c
2
(
x
−
μ
)
{\displaystyle \mathrm {erfc} ~{\sqrt {\frac {c}{2(x-\mu )}}}\!}
Espérance
+
∞
{\displaystyle +\infty \,}
Médiane
c
/
2
(
erf
−
1
(
1
/
2
)
)
2
{\displaystyle c/2({\textrm {erf}}^{-1}(1/2))^{2}\,}
μ
=
0
{\displaystyle \mu =0}
Mode
c
3
{\displaystyle {\frac {c}{3}}\,}
μ
=
0
{\displaystyle \mu =0}
Variance
+
∞
{\displaystyle +\infty \,}
Asymétrie
non définie
Kurtosis normalisé
non défini
Entropie
1
+
3
γ
+
ln
(
16
π
c
2
)
2
{\displaystyle {\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}\,}
Fonction génératrice des moments
non définie
Fonction caractéristique
e
i
μ
t
−
−
2
i
c
t
{\displaystyle \mathrm {e} ^{\mathrm {i} \mu t-{\sqrt {-2\mathrm {i} ct}}}\,}
modifier
En théorie des probabilités et en statistique , la loi de Lévy , nommée d'après le mathématicien Paul Lévy , est une loi de probabilité continue. En physique , plus précisément en spectroscopie , elle porte le nom de profil de van der Waals et décrit le profil de certaines raies spectrales .
Cette loi dépend de deux paramètres : un paramètre de position
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
[
μ
,
∞
[
{\displaystyle [\mu ,\infty [}
paramètre d'échelle
c
{\displaystyle c}
Si X suit une loi de Lévy, on notera :
X
∼
L
e
v
y
(
μ
,
c
)
{\displaystyle X\sim \mathrm {Levy} (\mu ,c)}
Avec la loi de Cauchy et la loi normale , c'est l'une des trois à être stable par convolution et à posséder une densité de probabilité exprimable analytiquement.
La densité de probabilité de la loi de Lévy est donnée par :
f
(
x
;
μ
,
c
)
=
{
c
2
π
1
(
x
−
μ
)
3
/
2
e
−
c
2
(
x
−
μ
)
si
x
>
μ
0
sinon
{\displaystyle f(x;\mu ,c)={\begin{cases}\displaystyle {\sqrt {\frac {c}{2\pi }}}{\frac {1}{(x-\mu )^{3/2}}}\mathrm {e} ^{-{\frac {c}{2(x-\mu )}}}&{\text{ si }}x>\mu \\0&{\text{ sinon}}\end{cases}}}
où
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
paramètre de position et
c
>
0
{\displaystyle c>0}
paramètre d'échelle . Comme toutes les lois stables , il existe une forme standard de la loi, définie par la densité
f
(
x
;
0
,
1
)
{\displaystyle f(x;0,1)}
y
=
x
−
μ
c
{\displaystyle y={\frac {x-\mu }{c}}}
f
(
x
;
μ
,
σ
)
{\displaystyle f(x;\mu ,\sigma )}
La loi de Lévy possède une queue lourde , exprimée par la formule :
f
(
x
;
μ
,
c
)
∼
x
→
∞
c
2
π
1
x
3
/
2
.
{\displaystyle f(x;\mu ,c)\,{\underset {x\rightarrow \infty }{\sim }}\,{\sqrt {\frac {c}{2\pi }}}~{\frac {1}{x^{3/2}}}.}
Cette propriété est illustrée par la représentation de la densité sur un repère log-log .
Densité de probabilité d la loi de Lévy sur un repère log-log.
La fonction de répartition de la loi de Lévy est donnée par :
F
(
x
;
μ
,
c
)
=
{
erfc
(
c
/
2
(
x
−
μ
)
)
si
x
>
μ
0
sinon
{\displaystyle F(x;\mu ,c)={\begin{cases}\displaystyle {\textrm {erfc}}\left({\sqrt {c/2(x-\mu )}}\right)&{\text{ si }}x>\mu \\0&{\text{ sinon}}\end{cases}}}
où erfc est la fonction d'erreur complémentaire.
La fonction caractéristique de la loi de Lévy est :
φ
(
t
;
μ
,
c
)
=
e
i
μ
t
−
−
2
i
c
t
.
{\displaystyle \varphi (t;\mu ,c)=\mathrm {e} ^{\mathrm {i} \mu t-{\sqrt {-2\mathrm {i} ct}}}.}
On peut écrire cette fonction caractéristique sous la forme plus classique des lois stables :
φ
(
t
;
μ
,
c
)
=
e
i
μ
t
−
|
c
t
|
1
/
2
(
1
−
i
sign
(
t
)
)
.
{\displaystyle \varphi (t;\mu ,c)=\mathrm {e} ^{\mathrm {i} \mu t-|ct|^{1/2}~(1-\mathrm {i} ~{\textrm {sign}}(t))}.}
La preuve de ce résultat utilise le théorème principal de Glasser .
Pour
μ
=
0
{\displaystyle \mu =0}
n -ième moment de la loi de Lévy est donné formellement par :
m
n
=
d
e
f
c
2
π
∫
0
∞
e
−
c
/
2
x
x
n
x
3
/
2
d
x
.
{\displaystyle m_{n}\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {\mathrm {e} ^{-c/2x}\,x^{n}}{x^{3/2}}}\,{\rm {d}}x.}
Cette intégrale diverge pour tout n >0, ainsi les moments de la loi de Lévy ne sont pas définis. La fonction génératrice des moments est donnée formellement par :
M
(
t
;
c
)
=
d
e
f
c
2
π
∫
0
∞
e
−
c
/
2
x
+
t
x
x
3
/
2
d
x
.
{\displaystyle M(t;c)\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {\mathrm {e} ^{-c/2x+tx}}{x^{3/2}}}\,{\rm {d}}x.}
L'intégrale diverge pour
t
>
0
{\displaystyle t>0}
Si
X
∼
Levy
(
μ
,
c
)
{\displaystyle X\sim {\textrm {Levy}}(\mu ,c)\,}
k
X
+
b
∼
Levy
(
k
μ
+
b
,
k
c
)
{\displaystyle kX+b\sim {\textrm {Levy}}(k\mu +b,kc)\,}
Si
X
∼
Levy
(
0
,
c
)
{\displaystyle X\,\sim \,{\textrm {Levy}}(0,c)}
X
∼
Inv-Gamma
(
1
2
,
c
2
)
{\displaystyle X\,\sim \,{\textrm {Inv-Gamma}}({\tfrac {1}{2}},{\tfrac {c}{2}})}
loi inverse-gamma )
La loi de Lévy est cas particulier de fonction de Pearson de type V.
Si
Y
∼
Normal
(
μ
,
σ
2
)
{\displaystyle Y\,\sim \,{\textrm {Normal}}(\mu ,\sigma ^{2})}
loi normale ) alors
(
Y
−
μ
)
−
2
∼
Levy
(
0
,
1
/
σ
2
)
{\displaystyle {(Y-\mu )}^{-2}\sim \,{\textrm {Levy}}(0,1/\sigma ^{2})}
Si
X
∼
Normal
(
μ
,
1
σ
)
{\displaystyle X\sim {\textrm {Normal}}(\mu ,{\tfrac {1}{\sqrt {\sigma }}})\,}
(
X
−
μ
)
−
2
∼
Levy
(
0
,
σ
)
{\displaystyle {(X-\mu )}^{-2}\sim {\textrm {Levy}}(0,\sigma )\,}
Si
X
∼
Levy
(
μ
,
c
)
{\displaystyle X\,\sim \,{\textrm {Levy}}(\mu ,c)}
X
∼
Stable
(
1
/
2
,
1
,
c
,
μ
)
{\displaystyle X\,\sim \,{\textrm {Stable}}(1/2,1,c,\mu )\,}
loi stable )
Si
X
∼
Levy
(
0
,
c
)
{\displaystyle X\,\sim \,{\textrm {Levy}}(0,c)}
X
∼
Scale-inv-
χ
2
(
1
,
c
)
{\displaystyle X\,\sim \,{\textrm {Scale-inv-}}\chi ^{2}(1,c)}
loi inverse-χ² changée d'échelle)
Si
X
∼
Levy
(
μ
,
c
)
{\displaystyle X\,\sim \,{\textrm {Levy}}(\mu ,c)}
(
X
−
μ
)
−
1
2
∼
FoldedNormal
(
0
,
1
/
c
)
{\displaystyle {(X-\mu )}^{-{\tfrac {1}{2}}}\sim \,{\textrm {FoldedNormal}}(0,1/{\sqrt {c}})}
loi normale repliée ) 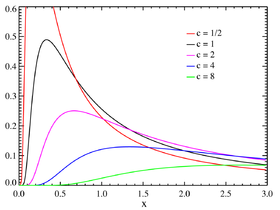




![{\displaystyle x\in ]\mu ,+\infty [\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba293074b6681b60f001fccf44dd8872d1deb506)


































