e (nombre)
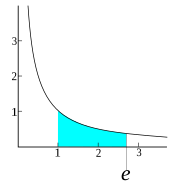
Le nombre e est la base des logarithmes naturels, c'est-à-dire le nombre défini par ln(e) = 1. Cette constante mathématique[a], également appelée nombre d'Euler[b] ou constante de Néper en référence aux mathématiciens Leonhard Euler et John Napier[c], vaut environ 2,71828.
Ce nombre est défini à la fin du XVIIe siècle, dans une correspondance entre Leibniz et Christian Huygens, comme étant la base du logarithme naturel. Autrement dit, il est caractérisé par la relation ln(e) = 1 ou de façon équivalente il est l'image de 1 par la fonction exponentielle, d'où la notation exp(x) = ex. La décomposition de cette fonction en série entière mène à la définition de e par Euler comme somme de la série[1] : Ce nombre apparaît aussi comme limite de la suite numérique de terme général et dans de nombreuses formules en analyse telles que l'identité d'Euler eiπ = −1 ou la formule de Stirling qui donne un équivalent de la factorielle. Il intervient aussi en théorie des probabilités ou en combinatoire.
Euler démontre en 1737 que e est irrationnel, donc que son développement décimal n'est pas périodique, et en donne une première approximation avec 23 décimales. Il explicite pour cela son développement en fraction continue. En 1873, Charles Hermite montre que le nombre e est même transcendant, c'est-à-dire qu'il n'est racine d'aucun polynôme non nul à coefficients entiers.
Définition par les logarithmes[modifier | modifier le code]
Logarithme népérien[modifier | modifier le code]

Au début du XVIIe siècle, le mathématicien écossais John Napier construit les premières tables de logarithmes, qui permettent de simplifier des calculs de produits et quotients mais aussi racines carrées, cubiques et autres. Elles consistent à associer à chaque nombre d'une liste un autre nombre (appelé logarithme), de façon qu'une relation de proportionnalité entre quatre termes de la première liste se traduise par des différences égales entre les termes correspondants de la seconde liste[2] : si a, b, c et d ont pour logarithmes respectifs A, B, C et D, alors la relation a⁄b = c⁄d est équivalente à la relation A − B = C − D.
Plus précisément, Napier fixe un rayon initial de dix millions[d] et construit une liste dans laquelle chaque nombre permet de calculer le suivant en lui soustrayant un dix-millionième de sa valeur. Ces opérations successives sont donc des multiplications itérées par 1 – 10–7 et la liste constitue une suite géométrique de premier terme 107. Le logarithme de chaque nombre de la liste étant son rang d'apparition, la formule du logarithme ainsi obtenu par Napier s'écrit alors :
- .
Napier interprète cette construction à l'aide d'un problème cinématique dans lequel un mobile se déplace à vitesse constante et un autre se déplace sur une longueur finie avec une vitesse proportionnelle à la distance qui lui reste à parcourir. En termes modernes, le problème se traduit donc par deux équations différentielles dont les solutions sont linéaire pour le premier mobile et exponentielle pour le second. En égalant les vitesses initiales des deux mobiles et en fixant à 107 la longueur à parcourir pour le second mobile, la position L du premier mobile s'obtient à partir de la distance restante x du premier mobile par la formule :
Or l'approximation affine du logarithme naturel en 1 permet d'approcher ln(1 − 10−7) par −10−7 avec une précision de l'ordre de 10−14, soit 7 chiffres significatifs. Les tables de valeurs obtenues par Napier offrent donc à la lecture les mêmes premières décimales que celles du logarithme naturel et en particulier, son logarithme vaut 107 entre les sinus de 21°35' et de 21°36, où l'on retrouve[3] les premières décimales de 1⁄e (à savoir 3678…). Mais ce nombre n'est pas mis en évidence par Napier.
Logarithme décimal[modifier | modifier le code]
En 1624, Henry Briggs, correspondant avec Napier, modifie les paramètres de construction des tables de logarithmes. D'abord il fixe à 0 le logarithme de 1, ce qui revient à choisir un rayon unitaire. Ses tables transforment alors les produits en sommes, ce qui s'écrit en formulation moderne : log(ab) = log(a) + log(b). Ensuite, il fixe à 1 le logarithme de 10, ce qui fait qu'une multiplication par 10 d'un nombre se traduit par un ajout d'une unité à son logarithme.
Briggs obtient ainsi une table de valeurs du logarithme décimal[4], fondé sur le système de numération en base 10, mais la notion de fonction n'a pas encore émergé à l'époque. En particulier, il n'y a pas de trace d'une évaluation d'un taux d'accroissement en 1, qui aurait pu faire apparaître une approximation de log10(e).
Logarithme naturel[modifier | modifier le code]
En 1647, Grégoire de Saint-Vincent met en évidence une relation analogue à celle du logarithme entre les aires de domaines délimités par une branche d'hyperbole et son asymptote. En 1661, Christian Huygens fait le lien entre les logarithmes et la quadrature de l'hyperbole, et en particulier celle d'équation x y = 1. Le logarithme naturel est donc mis en évidence, mais sa base (e) n'est pas identifiée.
C’est dans une lettre de Leibniz à Huygens que ce nombre est enfin identifié comme la base du logarithme naturel[5], vers 1690, mais Leibniz le note b.
Nouvelle notation[modifier | modifier le code]

Euler, dans un article écrit en 1727 ou 1728[6], est le premier à noter e « le nombre dont le logarithme est l'unité ». Il utilise cette notation, avec la même définition, dans une lettre à Goldbach en 1731[7].
Le choix de la lettre e comme un hommage au nom d'Euler lui-même[8] étant par conséquent peu probable, d'autres suppositions ont été avancées : première voyelle ou première lettre non utilisée dans un calcul littéral, initiale de « exponentielle », etc.[9].
Redéfinition par l'exponentielle[modifier | modifier le code]
Relation avec la base du logarithme naturel[modifier | modifier le code]
Euler voyait dans les fonctions exponentielles et les fonctions logarithmes des fonctions réciproques l'une de l'autre. Ecrivant l'équivalence , il appelait le logarithme l en question le logarithme de base a et remarquait que l(a) = 1. Selon cette correspondance, il existe un nombre appelé par Euler e vérifiant l'équivalence , ce nombre vérifie ln(e) = 1[10]. La fonction exponentielle admettant une décomposition en série entière, Euler obtient le développement de e comme série des inverses des factorielles des entiers naturels.
Selon Hervé Lehning[11], il aurait eu « l'intuition absolument géniale d'écrire l'exponentielle de base a quelconque comme un polynôme de l'exposant » :
Il va exprimer tous les coefficients en fonction de B. Voici comment. D'abord, en posant x=0, il obtient A=1. Puis, il calcule[12] :
mais puisque a2x= (ax)2, il pose également
donc,
Il développe le membre de droite de façon à pouvoir identifier les coefficients de gauche à ceux de droite : 2B=2B, 4C=B2+ 2C (d'où C=B2⁄2), 8D=2D+ 2BC (d'où D=B3⁄6), etc.
Il parvient donc à cette équation[12] :
La base e étant la seule permettant l'égalité entre l'exponentielle et sa dérivée, il reste à trouver B tel que ce polynôme et sa dérivée sont égaux. La solution est triviale : B=1. Enfin, on observe que 1, 2, 6, 24 sont les valeurs successives de la factorielle, ce qui mène Euler à conclure[12] :
dont une valeur approchée avait déjà été calculée par Isaac Newton en 1669[13].
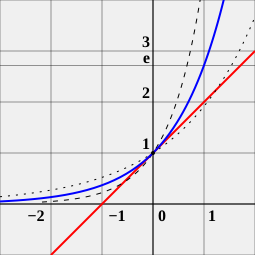
Les différentes caractérisations de la fonction exponentielle parmi les autres fonctions exponentielles de base quelconque permettent aussi de redéfinir e comme l'unique réel tel que la fonction qui à x associe ex coïncide avec sa dérivée en tout point, ou simplement au point 0 (ce qui est équivalent)[14].
Propriétés[modifier | modifier le code]
Irrationalité[modifier | modifier le code]
La première preuve de l'irrationalité de e est due à Euler (voir infra). Fourier donna la preuve plus simple suivante[15],[16], en utilisant la décomposition de e par la série exponentielle et en raisonnant par l'absurde.
Il s'agit de prouver que pour tout entier n > 0, le nombre ne n'est pas entier. Pour cela, il montre que n!e lui-même n'est pas entier, en le décomposant sous la forme , où les nombres x et y sont définis par : .
- Le nombre x est entier, comme somme des entiers n(n – 1)(n – 2)…(k + 1) (pour k de 0 à n) ;
- Le nombre y n'est pas entier. En effet, il est compris strictement entre 0 et 1[e].
Ainsi, n!e est somme d'un entier et d'un non-entier ; il n'est donc pas entier ; a fortiori, ne n'est pas entier. Cette conclusion étant valable quel que soit l'entier n > 0, e est irrationnel.
Fraction continue[modifier | modifier le code]
Une autre démonstration de l'irrationalité de e consiste à utiliser les fractions continues. Si la preuve est plus complexe, elle offre aussi plus de possibilités de généralisation.
En 1737, Euler a obtenu le développement en fraction continue de e[f] : . Ce développement étant infini, ce nombre est irrationnel.
En 1761, Lambert étend la preuve donnée par Euler et montre, à l'aide de développements en fractions continues généralisées, que pour tout rationnel r non nul (en particulier pour tout entier non nul), er est irrationnel[g].
Cette approche permet aussi d’établir que e n’est pas un irrationnel quadratique, c’est-à-dire n’est solution d’aucune équation du second degré à coefficients rationnels (cf. Fraction continue et approximation diophantienne).
Cependant, la mesure d'irrationalité de e est égale à 2, comme celle des nombres irrationnels algébriques ainsi que l'indique le théorème de Roth.
Transcendance[modifier | modifier le code]
Pour aller plus loin, c’est-à-dire que pour montrer que e n’est solution d’aucune équation du troisième degré à coefficients rationnels puis, qu’il est transcendant, ce qui signifie qu’il n’est solution d’aucune équation polynomiale à coefficients rationnels, de nouvelles idées sont nécessaires.
La transcendance de e fut établie par Charles Hermite en 1873[h], par une méthode préfigurant la théorie des approximants de Padé, développée en 1892 dans la thèse de son élève Henri Padé. Les différents approximants de Padé de la fonction exponentielle fournissent en effet de nombreuses expressions de e sous forme de fractions continues généralisées.
Puisque e est transcendant, er l'est aussi, pour tout rationnel r non nul (et plus généralement : f(e), pour toute fonction algébrique f non constante).
Le théorème de Gelfond-Schneider permet de démontrer également que, par exemple, eπ est transcendant, mais on ne sait pas encore, en 2020, si ee et πe sont transcendants ou non (il est cependant conjecturé que tous les nombres de cette forme le sont).
Il est également conjecturé que e est un nombre normal.
Applications[modifier | modifier le code]
Problème des intérêts composés[modifier | modifier le code]
En 1685, Jacques Bernoulli étudie le problème des intérêts composés en progression continue : si un montant a rapporte un montant b d'intérêts au bout d'un temps fini, on peut considérer que ces intérêts s'acquièrent linéairement en fonction du temps. Mais sur l'intervalle de temps considéré, ces intérêts devraient eux-mêmes produire des intérêts, et ainsi de suite. Bernoulli obtient ainsi une expression qui évoque le développement en série exponentielle[17].
Décimales connues[modifier | modifier le code]
Parmi les rationnels de numérateur et dénominateur inférieurs à 1 000, le plus proche de e est[18] 878323 ≈ 2,71827.
La valeur numérique de e tronquée à 15 décimales est[19] 2,718281828459045.
Le nombre de décimales connues de la constante e a beaucoup augmenté au cours des dernières décennies. Cette précision est due à l’augmentation des performances des ordinateurs ainsi qu’au perfectionnement des algorithmes[20],[21].
| Date | Nombre de décimales | Performance due à |
|---|---|---|
| 1748 | 23 | |
| 1853 | 137 | |
| 1871 | 205 |
|
| 1884 | 346 |
|
| 1949 | 2 010 |
|
| 1961 | 100 265 | |
| 1978 | 116 000 |
|
| 1er avril 1994 | 10 000 000 |
|
| 21 novembre 1999 | 1 250 000 000 |
|
| 16 juillet 2000 | 3 221 225 472 |
|
| 18 septembre 2003 | 50 100 000 000 |
|
| 27 avril 2007 | 100 000 000 000 |
|
| 6 mai 2009 | 200 000 000 000 |
|
| 5 juillet 2010 | 1 000 000 000 000 |
|
| 24 juin 2015 | 1 400 000 000 000 |
|
| 29 août 2016 | 5 000 000 000 000 |
|
| 3 janvier 2019 | 8 000 000 000 000 |
|
| 5 décembre 2020 | 31 415 926 535 897 |
|
Dans la culture informatique[modifier | modifier le code]
Le nombre e fait l'objet de nombreux hommages dans le milieu informatique.
Pour son introduction en bourse en 2004, Google a annoncé vouloir lever non pas un chiffre rond comme c'est généralement le cas, mais 2 718 281 828 $, soit e milliards de dollars (au dollar près)[33]. Google est aussi à l'origine d'une campagne de recrutement originale en juillet 2004 : des panneaux mentionnant « {first 10-digit prime found in the consecutive digits of e}.com » ({premier nombre premier à 10 chiffres trouvé dans les décimales successives de e}.com) affichés dans un premier temps dans la Silicon Valley, puis à Cambridge, Seattle et Austin incitaient les curieux à se rendre sur le site aujourd'hui disparu 7427466391.com. Là, le visiteur devait résoudre un problème encore plus difficile, qui lui-même le renvoyait sur le site Google Labs où il était invité à soumettre un CV[34],[35]. Le premier nombre premier à dix chiffres dans les décimales de e est 7 427 466 391, qui commence à la 99e décimale[19].
L'informaticien Donald Knuth a numéroté les différentes versions de son programme Metafont d'après les décimales de e : 2, 2,7, 2,71, 2,718, et ainsi de suite. De la même façon, les numéros de versions de son programme TeX approchent π[36].
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- La typographie des constantes mathématiques requiert l’utilisation de la police romaine, pour réserver l’italique aux variables.
- Ne pas confondre avec les nombres d'Euler (coefficients du développement de en série de Taylor), ni avec la constante d'Euler-Mascheroni (généralement notée γ), fréquemment appelée constante d'Euler.
- Par une variante orthographique de son nom.
- Ce rayon correspond au rayon d'un cercle dans lequel sont calculées les valeurs trigonométriques, variant donc entre 0 et 107 et non entre 0 et 1 comme actuellement.
- Voir par exemple .
- Voir la section « Exemple : le nombre e » de l'article « Fraction continue et approximation diophantienne ».
- Voir la section « Irrationalité » de l'article « Fraction continue et approximation diophantienne ».
- Voir l'article « Théorème d'Hermite-Lindemann ».
Références[modifier | modifier le code]
- (en) Encyclopedic Dictionary of Mathematics, 142.D.
- Simone Trompler, L'histoire des logarithmes, Les Cahiers du CeDoP, Université libre de Bruxelles, 2002, p. 5.
- Voir la table de valeurs du logarithme népérien pour un angle de 21°, p. 44.
- Briggs, Wallis, Ialley, Sharp, Mathematical tables, p. 27.
- Correspondance entre Huygens et Leibniz, p. 33.
- (la) L. Euler, « Meditatio in experimenta explosione tormentorum nuper instituta » (E853), manuscrit sur la puissance explosive des canons publié pour la première fois dans (la) L. Euler, Opera postuma mathematica et physica, et partiellement traduit dans (en) Florian Cajori, « Use of the letter e to represent 2.718... », dans D. E. Smith, A Source Book in Mathematics, McGraw-Hill, (lire en ligne), p. 95-99.
- Cajori 1929, p. 96.
- Suggéré par exemple par (en) Jonathan Sondow et Eric W. Weisstein, « e », sur MathWorld.
- (en) Jeff Miller, « Earliest Uses of Symbols for Constants », .
- (la)Leonhard Euler, Introductio in analysin infinitorum, 1748 (écrit en 1745), vol. 1 (E101), chap. 7.
- Hervé Lehning, L'univers des nombres : De l'Antiquité à Internet, Ixelles Éditions, , 320 p. (ISBN 978-2-87515-458-3, lire en ligne), p. 208.
- Lehning 2013, p. 209.
- (en) E – History, sur functions.wolfram.com.
- (en) Jerrold Marsden et Alan Weinstein, Calculus I, New York/Berlin/Heidelberg, Springer, , 2e éd. (1re éd. 1980) (ISBN 3-540-90974-5, lire en ligne), p. 319.
- Janot de Stainville, Mélange d'analyse Algébrique et de Géométrie, 1815, sur bibnum, accompagné d'une analyse de Norbert Verdier, L'irrationalité de e par Janot de Stainville, Liouville et quelques autres.
- Cette preuve figure dans Martin Aigner et Günter M. Ziegler, Raisonnements divins, p. 33-38, ainsi que celle de la généralisation suivante : pour tout rationnel non nul r, er est irrationnel.
- (la) J. Bernoulli, Opera, t. 1, p. 429, aperçu sur Google Livres.
- (en) David Wells, The Penguin Dictionary of Curious and Interesting Numbers (en), p. 46, cité par (en) Eli Maor, E : The Story of a Number, Princeton University Press, (lire en ligne), p. 37.
- Suite
 A001113 de l'OEIS.
A001113 de l'OEIS.
- (en) P. Sebah et X. Gourdon, The constant e and its computation.
- (en) X. Gourdon, Reported large computations with PiFast.
- Leonhard Euler, Introductio in Analysin Infinitorum (Lausanne, Switzerland: Marc Michel Bousquet & Co., 1748), volume 1, page 90.
- « We have computed e on a 7090 to 100,265D by the obvious program », p. 78 de (en) Daniel Shanks et John W. Wrench, « Calculation of Pi to 100,000 Decimals », Mathematics of Computation, vol. 16, no 77, , p. 76-99 (lire en ligne).
- (en) Stephen Wozniak, « The Impossible Dream: Computing e to 116,000 places with a Personal Computer », Byte Magazine, vol. 6, no 6, , p. 392.
- (en) Email from Robert Nemiroff and Jerry Bonnell – The Number e to 1 Million Digits.
- (en) Email from Xavier Gourdon to Simon Plouffe : « I have made a new e computation (with verification) : 1,250,000,000 digits. »
- (en) PiHacks message 177 – E to 3,221,225,472 D. Groups.yahoo.com.
- (en) PiHacks message 1071 – « Two new records : 50 billions for E and 25 billions for pi. » Groups.yahoo.com.
- (en) English Version of PI WORLD. Ja0hxv.calico.jp.
- (en) « A list of notable large computations of e », sur numberworld.org.
- (en) « y-cruncher - A Multi-Threaded Pi Program », sur numberworld.org.
- « e », sur www.numberworld.org (consulté le )
- Marianne Kalinowski, « Petites brèves du dimanche », Tom's Hardware, .
- (en) « Google recruits eggheads with mystery billboard », sur C|net.
- (en) Andreas Klappenecker, « CPSC 411 Design and Analysis of Algorithms ».
- (en) Donald Knuth, « The Future of TeX and Metafont », TeX Mag.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Lien externe[modifier | modifier le code]
- (en) John J. O'Connor et Edmund F. Robertson, « The number e », sur MacTutor, université de St Andrews.
- Alexandre Junod, « Le nombre d'Euler », Bulletin de la SSPMP, vol. 142, , p. 24-27 (lire en ligne)
Bibliographie[modifier | modifier le code]
- (en) Edward Kasner et James R. Newman, Mathematics and the Imagination (en), Dover, (1re éd. 1940), 400 p. (ISBN 978-0-486-32027-4, lire en ligne), p. 84
- Carl D. Olds, « The simple continued fraction expansion of the number e », The American Mathematical Monthly, vol. 77, no 9, , p. 968–974 (URL, consulté le ).
































