Kurtosis

En théorie des probabilités et en statistique, le kurtosis (du nom féminin grec ancien κύρτωσις, « courbure »), aussi traduit par coefficient d’acuité^[1], coefficient d’aplatissement et degré de voussure, est une mesure directe de l’acuité et une mesure indirecte de l'aplatissement de la distribution d’une variable aléatoire réelle. Il existe plusieurs mesures de l'acuité et le kurtosis correspond à la méthode de Pearson.

C’est le deuxième des paramètres de forme, avec le coefficient d'asymétrie (les paramètres fondés sur les moments d’ordre 5 et plus n’ont pas de nom propre).

Il mesure, abstraction faite de la dispersion (donnée par l’écart type), la répartition des masses de probabilité autour de leur centre, donné par l’espérance mathématique, c’est-à-dire, d’une certaine façon, leur concentration à proximité ou à distance du centre de probabilité.

Définitions[modifier | modifier le code]

Kurtosis non normalisé (coefficient d’aplatissement)[modifier | modifier le code]

Étant donné une variable aléatoire réelle $X$ d’espérance $\mu$ et d’écart type $\sigma$ , on définit son kurtosis non normalisé comme le moment d’ordre quatre de la variable centrée réduite :

\beta _{2}=\mathbb {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]

lorsque cette espérance existe. On a donc :

\beta _{2}={\frac {\mu _{4}}{\sigma ^{\ 4}}}

avec $\mu _{i}$ les moments centrés d’ordre $i$ .

Kurtosis normalisé (excès d’aplatissement)[modifier | modifier le code]

Le kurtosis non normalisé étant défini en fonction de moments centrés, il est malaisé à manipuler lorsqu’il s’agit de calculer celui de la somme de variables indépendantes.

On définit ainsi le kurtosis normalisé en fonction de cumulants :

\gamma _{2}={\frac {\kappa _{4}}{\kappa _{2}^{\ 2}}}

Sachant que $\mu _{2}=\kappa _{2}$ et $\mu _{4}=\kappa _{4}+3\kappa _{2}^{\ 2}$ , on a alors^[2]:

\gamma _{2}={\frac {\mu _{4}-3\mu _{2}^{\ 2}}{\mu _{2}^{\ 2}}}=\beta _{2}-3

Propriétés[modifier | modifier le code]

Dimension[modifier | modifier le code]

Les moments centrés $\mu _{i}$ et cumulants $\kappa _{i}$ ayant pour dimension celle de la variable $X$ élevée à la puissance $i$ , les kurtosis $\beta _{2}$ et $\gamma _{2}$ sont des grandeurs adimensionnelles.

Plage de valeur[modifier | modifier le code]

Soit la variable aléatoire réelle $Y=\left({\frac {X-\mu }{\sigma }}\right)^{2}$ . Cette variable aléatoire a pour espérance $\mathbb {E} (Y)={\frac {\mu _{2}}{\sigma ^{2}}}=1$ et pour variance $\operatorname {V} (Y)=\mathbb {E} \left(Y^{2}\right)-\mathbb {E} (Y)^{2}=\beta _{2}-1=\gamma _{2}+2$ . Sachant que $\operatorname {V} (Y)\geq 0$ , on en déduit alors que :

$\beta _{2}\geq 1$
$\gamma _{2}\geq -2$

Cette limite inférieure n’est atteinte que dans le cas où (à transformation affine près) la variable aléatoire X suit une loi de Bernoulli de paramètre $p=1/2$ (un seul tirage à pile ou face avec une pièce parfaitement équilibrée). Pour la loi normale, on a $\gamma _{2}=0$ .

Le kurtosis n’a pas de limite supérieure.

Somme de réalisations indépendantes[modifier | modifier le code]

Soient $X$ une variable aléatoire réelle et $Y=\sum _{1}^{n}X$ la somme de $n$ réalisations indépendantes de $X$ (exemple : la loi binomiale de paramètres $n$ et $p$ , somme de $n$ réalisations indépendantes de la loi de Bernoulli de paramètre $p$ ). Grâce à la propriété d’additivité des cumulants, on sait que $\kappa _{i}(Y)=n\kappa _{i}(X)$ , donc :

\gamma _{2}(Y)={\frac {n\kappa _{4}(X)}{(n\kappa _{2}(X))^{2}}}={\frac {\gamma _{2}(X)}{n}}

Typologie[modifier | modifier le code]

Un coefficient d’aplatissement élevé indique que la distribution est plutôt pointue en sa moyenne, et a des queues de distribution épaisses (fat tails en anglais, fat tail au singulier). Cela se déduit en considérant la distribution $Y$ définie plus haut, dont l’espérance vaut 1 et dont le moment centré d’ordre deux est le kurtosis non normalisé de $X$ . Comme son espérance est fixée, son moment d’ordre deux ne peut évoluer que par compensation : pour l’augmenter, il faut de l’inertie en position éloignée, contrebalancée par de l’inertie proche. En d’autres termes, on « pince » les flancs et les probabilités se déplacent par conséquent vers le centre et les extrémités.

Le terme d'« excès d’aplatissement », dérivé de kurtosis excess en anglais, utilisé pour le kurtosis normalisé peut être source d’ambiguïté. En effet, un excès d’aplatissement positif correspond à une distribution pointue et un excès d’aplatissement négatif à une distribution aplatie (on s’attendrait à l’inverse).

Distribution mésokurtique[modifier | modifier le code]

Si $\gamma _{2}=0$ , on parle de distribution mésokurtique (ou mésocurtique). La loi normale est un cas particulier de distribution mésokurtique pour laquelle le coefficient de dissymétrie $\gamma _{1}$ vaut 0.

Distribution leptokurtique[modifier | modifier le code]

Si $\gamma _{2}>0$ , on parle de distribution leptokurtique (ou leptocurtique). La notion de leptokurticité est très utilisée dans le milieu de la finance de marché, les échantillons ayant des extrémités plus épaisses que la normale, impliquant des valeurs anormales plus fréquentes^[3].

Distribution platikurtique[modifier | modifier le code]

Si $\gamma _{2}<0$ , on parle de distribution platykurtique (ou platycurtique, platikurtique, platicurtique). Pour une même variance, la distribution est relativement « aplatie », son centre et ses queues étant appauvries au profit des flancs.

Exemples de kurtosis pour quelques distributions absolument continues[modifier | modifier le code]

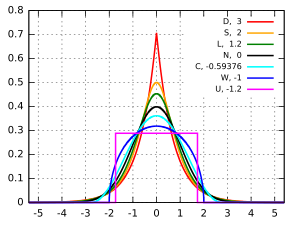
La figure suivante représente quelques distributions à densité unimodales centrées réduites symétriques ( $\mu =0$ , $\sigma =1$ et $\gamma _{1}=0$ ).

Loi de probabilité	Kurtosis normalisé	Symbole dans la figure	Couleur dans la figure
Loi de Laplace	3	D	Courbe rouge
Loi sécante hyperbolique	2	S	Courbe orange
Loi logistique	1,2	L	Courbe verte
Loi normale	0	N	Courbe noire
Loi du cosinus surélevé	-0,593762…	C	Courbe cyan
Loi triangulaire	-0,6
Loi du demi-cercle	-1	W	Courbe bleue
Loi uniforme continue	-1,2	U	Courbe magenta

Estimateur non biaisé[modifier | modifier le code]

Une utilisation naïve des définitions théoriques $\beta _{2}$ et $\gamma _{2}$ du coefficient d’aplatissement entraîne des mesures biaisées. Plusieurs logiciels de statistiques (SAS, Tanagra, Minitab, PSPP/SPSS et Excel par exemple, mais pas BMDP (it)) utilisent un estimateur non biaisé pour la loi normale du kurtosis normalisé^[4] :

G_{2}={\frac {K_{4}}{K_{2}^{2}}}={\frac {n(n+1)}{(n-1)(n-2)(n-3)}}{\frac {\sum _{i=1}^{n}(x_{i}-{\hat {\bar {x}}})^{4}}{K_{2}^{2}}}-3{\frac {(n-1)^{2}}{(n-2)(n-3)}}

où ${\hat {\bar {x}}}$ , $K_{2}$ et $K_{4}$ sont des estimateurs non biaisés respectivement de l’espérance, de la variance et du moment d'ordre 4 de la variable étudiée.

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Kurtosis, sur Wikimedia Commons

Notes et références[modifier | modifier le code]

↑ Geneviève Coudé-Gaussen, Les poussières sahariennes, John Libbey Eurotext, 1991, 485 p. (ISBN 978-0-86196-304-1, lire en ligne), p. 471.
↑ Voir Cumulant (statistiques)#Cumulants et moments.
↑ Régis Bourbonnais et Michel Terraza, Analyse des séries temporelles, 2^e édition, Dunod, 2008, p. 296.
↑ (en) D.N. Joanes et C.A. Gill, « Comparing Measures of Sample Skewness and Kurtosis », Journal of Statistical Societyt. Séries D (The statisticain), vol. 47, n^o 1,‎ 1998, p. 183-189, page184.

Articles connexes[modifier | modifier le code]

Portail des probabilités et de la statistique

[1] Geneviève Coudé-Gaussen, Les poussières sahariennes, John Libbey Eurotext, 1991, 485 p. (ISBN 978-0-86196-304-1, lire en ligne), p. 471.

[2] Voir Cumulant (statistiques)#Cumulants et moments.

[3] Régis Bourbonnais et Michel Terraza, Analyse des séries temporelles, 2^e édition, Dunod, 2008, p. 296.

[4] (en) D.N. Joanes et C.A. Gill, « Comparing Measures of Sample Skewness and Kurtosis », Journal of Statistical Societyt. Séries D (The statisticain), vol. 47, n^o 1,‎ 1998, p. 183-189, page184.

[1]

[2]

[3]

[4]