Loi binomiale
En théorie des probabilités et en statistique, la loi binomiale modélise la fréquence du nombre de succès obtenus lors de la répétition de plusieurs expériences aléatoires identiques et indépendantes.
Plus mathématiquement, la loi binomiale est une loi de probabilité discrète décrite par deux paramètres : n le nombre d'expériences réalisées, et p la probabilité de succès. Pour chaque expérience appelée épreuve de Bernoulli, on utilise une variable aléatoire qui prend la valeur 1 lors d'un succès et la valeur 0 sinon. La variable aléatoire, somme de toutes ces variables aléatoires, compte le nombre de succès et suit une loi binomiale. Il est alors possible d'obtenir la probabilité de k succès dans une répétition de n expériences :
Cette formule fait intervenir le coefficient binomial duquel provient le nom de la loi.
L'importance de cette loi est d'abord historique puisqu'elle a été l'objet d'étude du théorème de Moivre-Laplace, résultat du xviiie siècle fondateur des théorèmes de convergence. Une loi binomiale peut également être utilisée pour modéliser des situations simples de succès ou échec, un jeu de pile ou face par exemple. Le calcul de sa fonction de masse devient rapidement fastidieux lorsque n est grand, il est alors possible d'utiliser des approximations par d'autres lois de probabilité telles que la loi de Poisson ou la loi normale et d'utiliser des tables de valeurs.
La loi binomiale est utilisée dans divers domaines d'étude, notamment à travers des tests statistiques qui permettent d'interpréter des données et de prendre des décisions dans des situations dépendant de l'aléa. De par la simplicité de sa définition, c'est l'une des lois de probabilité étudiées dans les cours d'introduction à la théorie des probabilités.
Explication intuitive[modifier | modifier le code]

Premiers exemples[modifier | modifier le code]
Pile ou face[modifier | modifier le code]
Considérons n lancers successifs d'une pièce de monnaie. Alors le nombre de fois où la pièce apparaît du côté pile suit la loi binomiale où le nombre d'expériences réalisées est n et où la probabilité de succès est .
Lancer de dé[modifier | modifier le code]
Considérons n lancers successifs d'un dé à 6 faces. Alors le nombre de fois où l'on obtient un 1, suit la loi binomiale où le nombre d'expériences réalisées est n et où la probabilité de succès est .
Définition intuitive[modifier | modifier le code]
Une loi de Bernoulli décrit le comportement d'une expérience aléatoire qui possède deux résultats possibles traditionnellement appelés succès et échec[1]. Une telle expérience s'appelle une épreuve de Bernoulli. Par exemple, lors d'un lancer de pile ou face, on peut considérer qu'obtenir face est un succès et obtenir pile est un échec. Dans ce modèle, la probabilité de succès est une valeur fixe, c'est-à-dire qui reste constante à chaque renouvellement de l'expérience aléatoire. Cette probabilité de succès est notée p. Nous pouvons noter sa loi de probabilité :
On considère la situation où une telle expérience aléatoire (deux résultats possibles et une probabilité fixe) est répétée un certain nombre de fois de manière indépendante ; notons n ce nombre de fois. Cette répétition indépendante d'épreuves de Bernoulli s'appelle un schéma de Bernoulli ou simplement des épreuves de Bernoulli[2]. Une loi binomiale décrit le nombre de fois où le succès apparaît sur les n expériences effectuées. Le nombre de succès obtenus étant une valeur aléatoire, une loi binomiale est décrite grâce à la donnée des probabilités que le succès apparaisse précisément k fois sur les n essais.
Arbre de probabilité[modifier | modifier le code]
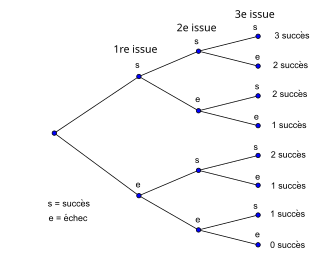
Une manière visuelle de représenter une suite d'expériences est d'utiliser un arbre de probabilité. Chaque épreuve est représentée par deux branches : l'une pour le succès, l'autre l'échec. À chaque extrémité, on rajoute deux branches (succès et échec) pour l'épreuve suivante. On recommence jusqu'au nombre total d'épreuves. À chaque extrémité finale, on peut compter le nombre de succès obtenus. Il suffit de multiplier le nombre de fois où il y a k succès par la probabilité d'obtenir k succès pour obtenir la probabilité correspondante de la loi binomiale.
Par exemple, on lance 3 fois de suite un dé équilibré à six faces et on s'intéresse au nombre de fois que le 1 apparaît. Il apparaît 0, 1, 2 ou 3 fois. Chaque lancer est indépendant des autres et la probabilité d'obtenir le 1 est de 1/6 sur chacun d'entre eux, autrement dit la probabilité qu'il n'apparaisse pas est de 5/6 à chaque lancer. Ainsi, pour chaque lancer, on considère une loi de Bernoulli de paramètre 1/6. Il y a trois configurations pour obtenir une seule fois le 1 : il apparaît au premier lancer ou au deuxième ou au troisième. Chacune de ces issues a la même probabilité d'apparaître : . La probabilité pour avoir une fois le 1 est alors : . On retrouve bien pour une loi binomiale b(3, 1/6). Il est possible de retrouver les autres probabilités de la même façon.
Définition mathématique[modifier | modifier le code]
La loi binomiale est une loi de probabilité discrète[3] à deux paramètres : et . Il est fréquent d'utiliser également le paramètre q = 1 – p pour avoir des expressions plus concises. Elle possède plusieurs définitions équivalentes :
Définition 1[4],[1] — La loi binomiale, de paramètres n et p, est la loi de probabilité d'une variable aléatoire X égale au nombre de succès rencontrés au cours d'une répétition de n épreuves de Bernoulli, p étant la probabilité de succès dans chacune d'entre elles.
Définition 2[5] — La loi binomiale, de paramètres n et p, est la loi de probabilité d'une variable aléatoire X telle que :
où sont des variables aléatoires indépendantes de loi de Bernoulli de même paramètre p.
Définition 3[3] — La loi binomiale, de paramètres n et p, est la loi de probabilité discrète d'une variable aléatoire X dont la fonction de masse est donnée par :
- pour .
On rappelle que des variables aléatoires et de loi discrète sont indépendantes si .
La fonction de masse donnée dans la définition 3 a bien un sens puisque la formule du binôme de Newton donne[6] : . La définition 2 est l'écriture mathématique de la définition 1[7].
La définition 3 est équivalente aux deux autres : on calcule explicitement la probabilité que k succès apparaissent dans n essais. Puisque les n répétitions sont indépendantes, la probabilité d'obtenir k succès et donc n – k échecs est : , dans le cas où on ne tient pas compte de la place des résultats[5],[8]. Il suffit alors de s'intéresser à la place des k succès et n – k échecs. C'est-à-dire, combien y a-t-il de manière de placer k succès parmi n résultats (sans s'occuper de l'ordre entre les succès) ? C'est le nombre de combinaisons de k éléments parmi n éléments[9] donné par le coefficient binomial . On retrouve alors la fonction de masse de la définition 3.
- Notation
Le fait qu'une variable aléatoire X suive une loi binomiale de paramètres n et p est noté[3],[5] : ; ou .
- Mesure de probabilité
Puisque la loi binomiale b(n, p) est une loi discrète, il est possible de la définir grâce à sa mesure de probabilité[10] :
- , où est la mesure de Dirac au point k.
Historique[modifier | modifier le code]
La loi binomiale fait partie des plus anciennes lois de probabilités étudiées[3]. Elle a été introduite par Jacques Bernoulli qui y fait référence en 1713 dans son ouvrage Ars Conjectandi. Entre 1708 et 1718, on découvre aussi la loi multinomiale (généralisation multi-dimensionnelle de la loi binomiale), la loi binomiale négative ainsi que l'approximation de la loi binomiale par la loi de Poisson, la loi des grands nombres pour la loi binomiale et une approximation de la queue de la loi binomiale[11].
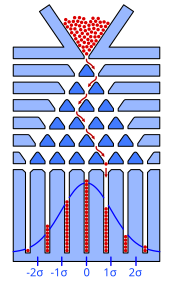
Grâce à l'expression de sa fonction de masse, la loi binomiale a été utilisée par plusieurs scientifiques pour réaliser des calculs dans des situations concrètes. C'est le cas d'Abraham de Moivre[a 1] qui réussit à trouver une approximation de la loi binomiale par la loi normale, il publie d'abord ses résultats en 1733 en latin[12] : Approximatio ad summam terminorum binomii (a + b)n in seriem expansi, puis les traduit pour les publier en 1738 dans The Doctrine of Chances (en)[12]. En 1812, Pierre-Simon de Laplace reprend ces travaux. Francis Galton crée la planche de Galton qui permet d'avoir une représentation physique de cette convergence[a 1]. En 1909, Émile Borel énonce et prouve, dans le cas de la loi binomiale, la première version de la loi forte des grands nombres[13].
Plus récemment, en 1914, McKendrick démontre que la loi binomiale est la solution d'un processus simple de naissance et d'émigration[14]. D'après les travaux de William Feller en 1957, elle peut aussi être vue comme la loi stationnaire pour le modèle des urnes d'Ehrenfest. Cette même année, Haight montre que la loi binomiale est liée à un problème de file d'attente[14].
La loi binomiale apparaît dans de nombreuses applications au XXe siècle[15] : en génétique, en biologie animale, en écologie végétale, pour les tests statistiques, dans différents modèles physiques tels que des réseaux téléphoniques[16] ou le modèle des urnes d'Ehrenfest, etc.
Le nom « binomiale » de cette loi provient[7],[a 1] de l'écriture de sa fonction de masse (voir ci-dessous) qui contient un coefficient binomial issu du développement du binôme : (p + q)n.
Représentation sous la forme d'un arbre[modifier | modifier le code]

Puisque la loi binomiale est une suite d'épreuves de Bernoulli, il est possible de la représenter grâce à un arbre de probabilité : chaque nœud représente le résultat d'une épreuve, les probabilités de succès et d'échecs sont représentés par deux branches distinctes rattachées à un nœud. Le graphique est donc un arbre binaire équilibré. Un arbre contenant n générations correspond à une loi binomiale b(n, p).
Si on indique les résultats de chaque épreuve sur les arêtes de l'arbre, il est possible de visualiser les différentes issues de la loi binomiale[17]. Si ce sont les valeurs des probabilités qui sont indiquées sur les arêtes, alors les probabilités de la loi binomiale apparaissent au bout des branches[18] (voir le graphique ci-contre).
Le graphique est un arbre de probabilité pour une loi binomiale de paramètre n = 3. Sur chaque branche sont indiquées les probabilités des différentes issues : par exemple branches droite, gauche puis droite ; c'est-à-dire échec, succès puis échec. Au bout des branches de l'arbre, apparaissent les probabilités de chaque issue de la loi binomiale b(3, p). C'est-à-dire pour les valeurs k = 0, 1, 2 ou 3, on obtient , , et . On retrouve ainsi les différents coefficients binomiaux :
Propriétés[modifier | modifier le code]
Moments[modifier | modifier le code]
Les plus connus sont l'espérance et la variance, que l'on déduit classiquement[a 2] de la définition 2 ci-dessus :
- .
Les moments factoriels de la loi binomiale de paramètres n et p sont[a 3],[a 4] :
.
Par conséquent[19], ses moments ordinaires sont[20] :
S(r, k) pk, avec comme premières valeurs[21] :
| (espérance) | |
On peut aussi les obtenir par la formule de récurrence
,
où le terme désigne la dérivée par rapport à la variable p.
Les moments inverses, c'est-à-dire avec , sont infinis[22].
- Moments centrés
Les moments centrés sont les moments de la différence entre la variable et sa moyenne[23],[21].
| ; (variance) | |
L'expression de la variance donne l'écart type[24] : .
Les moments centrés se calculent aussi par cette autre relation de récurrence[a 5],[21] :
.
- Écart moyen
L'Écart moyen (ou déviation moyenne) est la moyenne des écarts à la moyenne ; il est donné par[22] :
,
où est la partie entière de np.
Par exemple, si , , valeur à comparer avec l'écart-type : .
- Fréquence de succès
Grâce aux formules précédentes, on obtient les moments de la fréquence des succès[24] : :
| moment d'ordre 1 (ou espérance) de la fréquence de succès | ||
| moment centré d'ordre 2 (ou variance) de la fréquence de succès | ||
| moment centré d'ordre 4 de la fréquence de succès |
L'expression de la variance de la fréquence donne l'écart type de la fréquence des succès : .
- Covariance
On considère deux variables aléatoires et , pas forcément indépendantes, de lois binomiales respectives et . La covariance permet d'évaluer la dépendance entre les deux variables :
- .
Propriétés et caractérisations[modifier | modifier le code]
- Valeurs descriptives de la loi
- Le coefficient d'asymétrie d'une loi binomiale b(n, p) est[25] : . L'asymétrie de la loi binomiale b(n, p) est positive[26] si p < 1/2 et négative si p > 1/2. La loi est symétrique si et seulement si p = 1/2.
- La médiane de la loi binomiale est ou , le signe désigne la partie entière. Ces valeurs s'obtiennent grâce à la formule[a 6] : (cette borne étant optimale).
- Le mode de la loi binomiale b(n, p) est la valeur , elle est la valeur de plus grande probabilité.
Si np est un entier, alors le mode, la moyenne et la médiane valent tous trois np.
- Propriétés de stabilité
- Si X suit une loi binomiale b(n, p), alors[5] Y = n – X suit une loi b(n, 1 – p). Cette symétrie donne les relations suivantes pour la fonction de répartition et pour la fonction de masse[27],[28] : et .
- Si les variables aléatoires indépendantes et sont de lois binomiales respectives et , alors la variable aléatoire est de loi binomiale . Cette propriété peut s'obtenir grâce à l'expression des fonctions caractéristiques ou grâce à l'écriture sous forme de somme de variables de Bernoulli[29].
- Inégalités
- L'inégalité de Bienaymé-Tchebychev pour une variable aléatoire X suivant la loi binomiale b(n, p) est obtenue grâce aux moments[24] :
- .
- L'inégalité de Hoeffding pour une variable aléatoire X de loi b(n, p) est plus précise que l'inégalité de Bienaymé-Tchebychev lorsque x est grand, elle s'écrit[30] :
- .
- L'inégalité de Kolmogorov s'écrit pour une somme de variables aléatoires indépendantes. Pour des variables aléatoires indépendantes de loi de Bernoulli, la somme suit une loi binomiale b(k, p) recentrée, l'inegalité s'écrit alors[31] :
- .
- Caractérisations
- En 1964, un cas particulier d'un théorème de Patil et Seshadri énonce[32] : si la loi conditionnelle de X + Y sachant X est une loi hypergéométrique de paramètres m et n, alors X et Y suivent des lois binomiales de paramètres respectifs et où est arbitraire.
- En 1973, Kagan, Linnik et Rao donnent plusieurs caractérisations en considérant des marches aléatoires à pas binomiaux sur un réseau avec des temps d'arrêt markoviens[32].
- En 1991, Ahmed démontre qu'une variable aléatoire X suit une loi binomiale variable aléatoire b(n, p) si et seulement si[32] où .
Fonction de répartition[modifier | modifier le code]

La fonction de répartition d'une variable aléatoire X suivant la loi binomiale b(n, p) est donnée par[23] :
où est la partie entière de x.
Même s'il existe une expression de la fonction de répartition, son calcul n'est pas facile[33] à cause des coefficients binomiaux , notamment lorsque n est grand. Il existe alors des tables de valeurs (voir ci-dessous). Des théorèmes d'approximation ont été développés[33] pour approcher de manière théorique et calculatoire cette fonction de répartition (voir ci-dessous). L'expression suivante provient du lien entre la loi binomiale et la loi bêta[23] (voir ci-dessous) : pour
où B est la fonction bêta. il est alors possible d'écrire la fonction de répartition grâce à la fonction bêta incomplète[34] :
- .
Fonctions caractéristique et génératrice[modifier | modifier le code]
La fonction caractéristique d'une variable aléatoire X suivant la loi binomiale b(n, p) est donnée par[24] :
- .
La fonction génératrice des moments d'une variable aléatoire X suivant la loi binomiale b(n, p) est donnée par[23] :
- .
On déduit directement la fonction génératrice des cumulants[14] :
- ,
et la fonction génératrice des cumulants factoriels[14] :
- .
Lien avec d'autres lois[modifier | modifier le code]
Loi de Bernoulli[modifier | modifier le code]
Rappelons que la loi binomiale de paramètres et est la loi de la somme de n variables aléatoires indépendantes de loi de Bernoulli de même paramètre p.
Ainsi, la loi binomiale b(1, p) est une loi de Bernoulli de paramètre p.
C'est par cette représentation du nombre de succès et d'échecs dans une suite d'épreuves que la loi binomiale est source de nombreuses applications[35].
Lois réciproques[modifier | modifier le code]
Les lois suivantes ont un lien avec la loi binomiale grâce à leur fonctions de répartition. Lorsque le nombre de succès k est fixé, elles donnent la loi du nombre d'épreuves nécessaires (loi binomiale négative) ou la loi du paramètre p (lois bêta ou de Fisher). En ce sens, elles peuvent servir de lois réciproques.
- La loi binomiale b(n, p) donne le nombre de succès dans une succession de n épreuves indépendantes. La loi binomiale négative, ou loi de Pascal, est le nombre d'épreuves nécessaires pour obtenir k succès[36]. le terme négatif provient de l'écriture de la fonction de masse qui contient un coefficient binomial avec un terme négatif[a 7].
De plus, si X suit une loi et si Y suit une loi b(n + k, p) alors[37],[38], pour k entre 0 et n :
, où est la fonction bêta incomplète. Autrement dit : la probabilité qu'il faille au moins n épreuves pour avoir k succès est égale à la probabilité qu'il y ait au plus k succès en n + k épreuves. - Grâce au calcul de la fonction de répartition de la loi bêta donnée par la fonction bêta incomplète , on obtient[a 7],[28], pour k entre 0 et n :
- où X suit une loi bêta de paramètres k + 1 , n – k et Y suit une loi binomiale b(n, p).
- La loi binomiale est liée à la loi de Fisher par la propriété suivante[a 7],[39] : si Y suit une loi binomiale b(n, p) alors, pour k entre 0 et n :
- où F suit une loi de Fischer de paramètres .
- La relation précédente permet de trouver les quantiles de la loi binomiale[39].
Autres lois[modifier | modifier le code]
- La loi binomiale (doublement) tronquée de paramètres et est la loi binomiale b(n, p) avec telle que les valeurs dans et dans sont enlevées[40]. La fonction de masse de cette loi est donnée par l'expression : pour
- De la même manière, il est possible de définir la loi binomiale (simplement) tronquée[40] en omettant uniquement les valeurs entre 0 et ou entre et .
- La loi binomiale positive ou loi binomiale tronquée en 0 est la loi binomiale b(n, p) dont on retire la valeur 0. Sa fonction de masse est : . De la même manière il est possible de définir la loi binomiale négative.
- La loi multinomiale est la généralisation multi-dimensionnelle de la loi binomiale[23] dans le sens où la loi multinomiale modélise une succession d'épreuves dont chacune possède plusieurs issues, pas uniquement succès ou échec. Cette loi multidimensionnelle donne les probabilités du nombre d'apparition des différentes issues dans une succession d'épreuves indépendantes[a 7].
- La loi bêta-binomiale est construite grâce à un mélange de loi[41] : une variable aléatoire qui suit une loi binomiale dont le paramètre est une variable aléatoire qui suit une loi bêta , est de loi bêta-binomiale de paramètres . Cette loi binomiale est similaire à la loi hypergéométrique négative (en), il suffit de changer les paramètres[42].
- La fonction de masse d'une variable Y de loi hypergéométrique de paramètres est donnée par : . Elle correspond au nombre tirages gagnants dans une expérience de n tirages simultanés dans une urne contenant A boules et une proportion de p boules gagnantes.
- Si le nombre de boules augmente, c'est-à-dire A tend vers l'infini, et si p/A tend vers une valeur , alors la loi hypergéométrique converge vers une loi binomiale[43] b(n, p').
- Autrement dit, si la taille de la population (A) est grande par rapport à la taille de l'échantillon (n), alors les tirages peuvent être convenablement représentés par une loi binomiale de paramètre p' égal au pourcentage (p) d'éléments ayant le caractère étudié.
- De plus, si et sont deux variables aléatoires indépendantes de loi binomiale respectives et , alors la loi de sachant que est la loi hypergéométrique de paramètres[29] : et .
Convergences et approximations[modifier | modifier le code]
Pour de grandes valeurs de n, le calcul des fonctions de masse et de répartition deviennent vite fastidieux. Une méthode est d'approcher ces valeurs grâce aux théorèmes limites. La loi (faible ou forte) des grands nombres permet d'approcher la moyenne de la loi binomiale. Pour obtenir des valeurs approchées de la fonction de répartition, il est possible d'utiliser l'approximation normale ou l'approximation par la loi de Poisson. L'approximation normale est plus performante lorsque le paramètre p n'est pas trop proche de 0 ou de 1, sinon l'approximation par la loi de Poisson donne de meilleurs résultats[44].
Loi des grands nombres[modifier | modifier le code]
La loi faible des grands nombres, appliquée à un processus de Bernoulli de paramètre p, garantit que pour toute suite (Xn) de variables aléatoires, définies sur un même espace probabilisé, et de lois respectives b(n, p) (cf. définition 2 ci-dessus), on a, pour tout : Plus précisément, puisque l'espérance et la variance de Xn sont respectivement égales à np et np(1 – p), l'inégalité de Bienaymé-Tchebychev montre que[24] : Cela peut s'interpréter grossièrement de la manière suivante. Si l'on sait que lors d'une expérience aléatoire (tirage d'un individu dans une population de grande taille, lancer d'une pièce…) la probabilité d'apparition de la propriété A est p(A), alors la fréquence d'apparition de la propriété A au cours de n expériences de ce type (tirages de n individus dans une population de taille très supérieure à n, n lancers de pièce…) est souvent voisine de p(A), avec une probabilité d'autant meilleure que n est grand et que p(A) est proche de 0 ou 1.
Il existe de meilleures majorations de cette probabilité, l'inégalité de Hoeffding donne[a 8] :
Convergence vers la loi de Poisson[modifier | modifier le code]
- Convergence
Considérons une loi binomiale b(n, p) telle que les paramètres n et p sont liés par la formule : où est fixé. Lorsque n tend vers l'infini, et donc p tend vers 0, alors[45] : . Autrement dit, la probabilité qu'une variable de loi binomiale prenne la valeur k converge (lorsque n devient grand) vers la probabilité qu'une variable de loi de Poisson prenne la valeur k. Le paramètre p converge alors vers 0, il correspond donc à un évènement de probabilité très faible, la loi de Poisson est alors appelée loi des évènements rares[45]. Par sommation, on obtient alors le résultat[46] :
où est la partie entière, X est une variable de loi binomiale et Y de loi de Poisson . Cette limite montre la convergence en loi de la loi binomiale (avec les conditions précédentes) vers la loi de Poisson. Une expression plus détaillée de la convergence peut être donnée par la formule[47],[23] : avec lorsque n tend vers l'infini et est le comparateur asymptotique.

En 1953, Iouri Prokhorov donne une majoration de l'erreur totale d'approximation entre la fonction de répartition d'une loi binomiale b(n, p) et une loi de Poisson [48] : . Il est également possible de borner le ratio entre les deux fonctions de répartition[48] :
- Approximation
Grâce à la convergence ci-dessus, il est possible d'approcher les probabilités de la loi binomiale par la loi de Poisson. En pratique, le cas s'applique lorsque n est grand et donc p petit. Différentes valeurs sont proposées[47],[45],[49],[50] :
- , lorsque (ce qui fait ) ;
- , lorsque (ce qui fait ) ;
- , lorsque (ce qui fait ) ;
- ;
- , lorsque ;
- et .
L'idée commune de toutes ces propositions est d'avoir la valeur np stable lorsque n est grand et p petit.
Convergence vers la loi normale[modifier | modifier le code]

- Convergence
Le théorème de Moivre-Laplace, énoncé en 1733, montre qu'une variable aléatoire de loi binomiale, convenablement renormalisée, converge en loi vers une variable aléatoire de loi normale. Ce résultat peut s'énoncer grâce aux fonctions de répartition des deux lois. Considérons une variable aléatoire X de loi binomiale b(n, p), la variable aléatoire X renormalisée est la variable aléatoire centrée et réduite, c'est-à-dire : . Si l'on note la fonction de répartition de la loi normale, alors :
- Théorème de Moivre-Laplace : pour tout ,
Bien qu'Abraham de Moivre n'ait énoncé ce résultat que dans le cas d'une loi binomiale[51], cette convergence est généralisée dans le cas d'autres lois, c'est le théorème central limite. Ce théorème permet d'approcher une loi discrète par une loi continue, il est alors utile d'ajouter un coefficient, dit correction de continuité, afin d'améliorer les approximations futures (voir ci-dessous). La convergence précédente peut alors s'écrire sous forme d'équivalence lorsque n tend vers l'infini[52] : pour tout
L'erreur commise par l'approximation est estimée par l'inégalité de Berry-Esseen dont la constante est régulièrement améliorée, elle fournit une borne de la différence entre les deux fonctions de répartition lorsque n est grand[53],[a 9], pour X une variable aléatoire de loi binomiale b(n, p) et Y de loi normale de fonction de répartition notée : . Une expression plus détaillée de la convergence peut être donnée par la formule avec correction de continuité[23] : uniformément pour toute variable x, lorsque n tend vers l'infini et où est le comparateur asymptotique. D'autres approximations plus fines ont été étudiées[54], par exemple par Laplace (1820), Prokhorov (1953) ou Peizer et Pratt (en) (1968).
- Approximation
Grâce aux théorèmes de convergence ci-dessus, lorsque n est grand, les probabilités de la binomiale renormalisée peuvent être approchées par les valeurs des probabilités de la loi normale. Il existe plusieurs règles sur les paramètres n et p pour que l'approximation soit valable[55],[50],[56],[57] :
- , et ;
- ou ;
- et .
L'influence de ces paramètres sur l'approximation a été finement étudiée dans les années 1990, par exemple[55] : pour n fixé, l'erreur absolue minimale est atteinte pour p = 1/2 ; l'erreur absolue est inférieure à .
Tables de la loi binomiale[modifier | modifier le code]
Des tables de la fonction de masse et de la fonction de répartition de la loi binomiale ont été publiées en 1950 par le National Bureau of Standards puis en 1955 dans National of the Computation Laboratory et par Rao et al. en 1985[58].
Grâce aux relations de symétrie (voir ci-dessus), il suffit[27],[28] de donner des tables de valeurs pour .
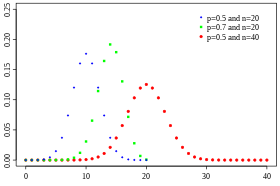
Valeurs de la fonction de masse[modifier | modifier le code]
Les tables de valeurs suivantes[49] donnent les valeurs de la fonction de masse de la loi binomiale b(n, p) pour différentes valeurs de n.
- Exemples : Si X suit une loi , alors . Si Y suit une loi , alors .
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,50 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,7738 | 0,5905 | 0,4437 | 0,3277 | 0,2373 | 0,1681 | 0,1160 | 0,0778 | 0,0312 |
| 1 | 0,2036 | 0,3281 | 0,3915 | 0,4096 | 0,3955 | 0,3601 | 0,3124 | 0,2592 | 0,1562 |
| 2 | 0,0214 | 0,0729 | 0,1382 | 0,2048 | 0,2637 | 0,3087 | 0,3364 | 0,3456 | 0,3125 |
| 3 | 0,0011 | 0,0081 | 0,0244 | 0,0512 | 0,0879 | 0,1323 | 0,1811 | 0,2304 | 0,3105 |
| 4 | 0,0000 | 0,0005 | 0,0022 | 0,0064 | 0,0146 | 0,0283 | 0,0488 | 0,0768 | 0,1562 |
| 5 | 0,0000 | 0,0000 | 0,0001 | 0,0003 | 0,0010 | 0,0024 | 0,0053 | 0,0102 | 0,0312 |
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,50 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,5987 | 0,3487 | 0,1969 | 0,1074 | 0,0563 | 0,0282 | 0,0135 | 0,0060 | 0,0010 |
| 1 | 0,3151 | 0,3874 | 0,3474 | 0,2684 | 0,1877 | 0,1211 | 0,0725 | 0,0403 | 0,0098 |
| 2 | 0,0746 | 0,1937 | 0,2759 | 0,3020 | 0,2816 | 0,2335 | 0,1757 | 0,1209 | 0,0439 |
| 3 | 0,0105 | 0,0574 | 0,1298 | 0,2013 | 0,2503 | 0,2668 | 0,2522 | 0,2150 | 0,1172 |
| 4 | 0,0010 | 0,0112 | 0,0401 | 0,0881 | 0,1460 | 0,2001 | 0,2377 | 0,2508 | 0,2051 |
| 5 | 0,0001 | 0,0015 | 0,0085 | 0,0264 | 0,0584 | 0,1029 | 0,1536 | 0,2007 | 0,2461 |
| 6 | 0,0000 | 0,0001 | 0,0012 | 0,0055 | 0,0162 | 0,0368 | 0,0689 | 0,1115 | 0,2051 |
| 7 | 0,0000 | 0,0000 | 0,0001 | 0,0008 | 0,0031 | 0,0090 | 0,0212 | 0,0425 | 0,1172 |
| 8 | 0,0000 | 0,0000 | 0,0000 | 0,0001 | 0,0004 | 0,0014 | 0,0043 | 0,0106 | 0,0439 |
| 9 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0001 | 0,0005 | 0,0016 | 0,0098 |
| 10 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0001 | 0,0010 |
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,50 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,3585 | 0,1216 | 0,0388 | 0,0115 | 0,0032 | 0,0008 | 0,0002 | 0,0000 | 0,0000 |
| 1 | 0,3774 | 0,2702 | 0,1368 | 0,0576 | 0,0211 | 0,0068 | 0,0020 | 0,0005 | 0,0000 |
| 2 | 0,1887 | 0,2852 | 0,2293 | 0,1369 | 0,0669 | 0,0278 | 0,0100 | 0,0031 | 0,0002 |
| 3 | 0,0596 | 0,1901 | 0,2428 | 0,2054 | 0,1339 | 0,0716 | 0,0323 | 0,0123 | 0,0011 |
| 4 | 0,0133 | 0,0898 | 0,1821 | 0,2182 | 0,1897 | 0,1304 | 0,0738 | 0,0350 | 0,0046 |
| 5 | 0,0022 | 0,0319 | 0,1028 | 0,1746 | 0,2023 | 0,1789 | 0,1272 | 0,0746 | 0,0148 |
| 6 | 0,0003 | 0,0089 | 0,0454 | 0,1091 | 0,1686 | 0,1916 | 0,1712 | 0,1244 | 0,0370 |
| 7 | 0,0000 | 0,0020 | 0,0160 | 0,0545 | 0,1124 | 0,1643 | 0,1844 | 0,1659 | 0,0739 |
| 8 | 0,0000 | 0,0004 | 0,0046 | 0,0222 | 0,0609 | 0,1144 | 0,1614 | 0,1797 | 0,1201 |
| 9 | 0,0000 | 0,0001 | 0,0011 | 0,0074 | 0,0271 | 0,0654 | 0,1158 | 0,1597 | 0,1602 |
| 10 | 0,0000 | 0,0000 | 0,0002 | 0,0020 | 0,0099 | 0,0308 | 0,0686 | 0,1171 | 0,1762 |
| 11 | 0,0000 | 0,0000 | 0,0000 | 0,0005 | 0,0030 | 0,0120 | 0,0336 | 0,0710 | 0,1602 |
| 12 | 0,0000 | 0,0000 | 0,0000 | 0,0001 | 0,0008 | 0,0039 | 0,0136 | 0,0355 | 0,1201 |
| 13 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0002 | 0,0010 | 0,0045 | 0,0146 | 0,0739 |
| 14 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0002 | 0,0012 | 0,0049 | 0,0370 |
| 15 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0003 | 0,0013 | 0,0148 |
| 16 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0003 | 0,0046 |
| 17 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0011 |
| 18 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0002 |
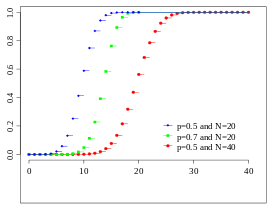
Valeurs de la fonction de répartition[modifier | modifier le code]
Les tables de valeurs suivantes[59] donnent les valeurs de la fonction de répartition de la loi binomiale b(n, p) pour différentes valeurs de n.
- Exemples : Si X suit une loi , alors . Si Y suit une loi , alors .
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,50 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,7738 | 0,5905 | 0,4437 | 0,3277 | 0,2373 | 0,1681 | 0,1160 | 0,0778 | 0,0312 |
| 1 | 0,9774 | 0,9185 | 0,8352 | 0,7373 | 0,6328 | 0,5282 | 0,4284 | 0,3370 | 0,1875 |
| 2 | 0,9988 | 0,9914 | 0,9734 | 0,9421 | 0,8965 | 0,8369 | 0,7648 | 0,6826 | 0,5000 |
| 3 | 1,0000 | 0,9995 | 0,9978 | 0,9933 | 0,9844 | 0,9692 | 0,9460 | 0,9130 | 0,8125 |
| 4 | 1,0000 | 1,0000 | 0,9999 | 0,9997 | 0,9990 | 0,9976 | 0,9947 | 0,9898 | 0,9688 |
| 5 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,50 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,5987 | 0,3487 | 0,1969 | 0,1074 | 0,0563 | 0,0282 | 0,0135 | 0,0060 | 0,0010 |
| 1 | 0,9139 | 0,7361 | 0,5443 | 0,3758 | 0,2440 | 0,1493 | 0,0860 | 0,0464 | 0,0107 |
| 2 | 0,9885 | 0,9298 | 0,8202 | 0,6778 | 0,5256 | 0,3828 | 0,2616 | 0,1673 | 0,0547 |
| 3 | 0,9990 | 0,9872 | 0,9500 | 0,8791 | 0,7759 | 0,6496 | 0,5138 | 0,3823 | 0,1719 |
| 4 | 0,9999 | 0,9984 | 0,9901 | 0,9672 | 0,9219 | 0,8497 | 0,7515 | 0,6331 | 0,3770 |
| 5 | 1,0000 | 0,9999 | 0,9986 | 0,9936 | 0,9803 | 0,9527 | 0,9051 | 0,8338 | 0,6230 |
| 6 | 1,0000 | 1,0000 | 0,9999 | 0,9991 | 0,9965 | 0,9894 | 0,9740 | 0,9452 | 0,8281 |
| 7 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9996 | 0,9984 | 0,9952 | 0,9877 | 0,9453 |
| 8 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9995 | 0,9983 | 0,9893 |
| 9 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9990 |
| 10 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,50 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,3585 | 0,1216 | 0,0388 | 0,0115 | 0,0032 | 0,0008 | 0,0002 | 0,0000 | 0,0000 |
| 1 | 0,7358 | 0,3817 | 0,1756 | 0,0692 | 0,0243 | 0,0076 | 0,0021 | 0,0005 | 0,0000 |
| 2 | 0,9245 | 0,6769 | 0,4049 | 0,2061 | 0,0913 | 0,0355 | 0,0121 | 0,0036 | 0,0002 |
| 3 | 0,9841 | 0,8670 | 0,6477 | 0,4114 | 0,2252 | 0,1071 | 0,0444 | 0,0160 | 0,0013 |
| 4 | 0,9974 | 0,9568 | 0,8298 | 0,6296 | 0,4148 | 0,2375 | 0,1182 | 0,0510 | 0,0059 |
| 5 | 0,9997 | 0,9887 | 0,9327 | 0,8042 | 0,6172 | 0,4164 | 0,2454 | 0,1256 | 0,0207 |
| 6 | 1,0000 | 0,9976 | 0,9781 | 0,9133 | 0,7858 | 0,6080 | 0,4166 | 0,2500 | 0,0577 |
| 7 | 1,0000 | 0,9996 | 0,9941 | 0,9679 | 0,8982 | 0,7723 | 0,6010 | 0,4159 | 0,1316 |
| 8 | 1,0000 | 0,9999 | 0,9987 | 0,9900 | 0,9591 | 0,8867 | 0,7624 | 0,5956 | 0,2517 |
| 9 | 1,0000 | 1,0000 | 0,9998 | 0,9974 | 0,9861 | 0,9520 | 0,8782 | 0,7553 | 0,4119 |
| 10 | 1,0000 | 1,0000 | 1,0000 | 0,9994 | 0,9961 | 0,9829 | 0,9468 | 0,8725 | 0,5881 |
| 11 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9991 | 0,9949 | 0,9804 | 0,9435 | 0,7483 |
| 12 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,998 | 0,9987 | 0,9940 | 0,9790 | 0,8684 |
| 13 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9997 | 0,9985 | 0,9935 | 0,9423 |
| 14 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9997 | 0,9984 | 0,9793 |
| 15 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9997 | 0,9941 |
| 16 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9987 |
| 17 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9998 |
| 18 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Tests et applications[modifier | modifier le code]
Tests[modifier | modifier le code]
D'une manière générale, un test statistique permet de rejeter, ou non, une hypothèse dite hypothèse nulle. L'idée principale est de prendre un échantillon et de vérifier si l'hypothèse est vraie pour chaque élément de l'échantillon. Si on considère que les éléments sont indépendants, on compte donc le nombre d'éléments vérifiant une propriété, il y a donc présence de la loi binomiale. On compare si la proportion observée est significativement éloignée de la probabilité théorique de la loi binomiale[60]. Ce test est appelé un test binomial. On peut utiliser aussi la loi normale lorsque la taille de l'échantillon est grand.
Il est possible d'effectuer un test statistique sur la conformité des valeurs des paramètres d'une loi de probabilité, notamment d'une loi binomiale, par rapport aux paramètres théoriques attendus pour la population étudiée[61]. Le test de conformité de l'indice de dispersion s'applique dans ce cas[62]. Cet indice de dispersion est le quotient de la somme des carrés des écarts et de la moyenne. Si sont les valeurs étudiées de moyenne notée alors l'indice est : . Grâce à une Loi du χ² ou une loi normale, le test rejette l'hypothèse de la valeur que prend le paramètre p de la loi binomiale[62].
Il est également possible de tester l'égalité de deux variables aléatoires de lois binomiales. Soient et deux variables aléatoires de lois respectives et . On souhaite tester si , c'est l'hypothèse du test. Par le théorème central limite, l'estimateur suit une loi normale lorsque est grand. Il en est de même avec . En considérant l'hypothèse vraie, on peut montrer que suit une loi normale centrée réduite[63]. On rejette alors l'hypothèse au niveau de confiance 0,95 si .
Autres applications[modifier | modifier le code]
Par définition la somme de variables aléatoires indépendantes de loi de Bernoulli suit une loi binomiale. Un exemple typique de phénomène suivant une loi de Bernoulli est le lancer d'une pièce pour un pile ou face[35]. Le nombre de succès, par exemple le nombre de fois où l'on obtient pile, suit donc une loi binomiale. De nombreuses situations peuvent être modélisées par cet exemple ce qui donne son importance à la loi[35].
En génétique, lors de la reproduction, chaque gène est composée de deux allèles qui sont issus des deux parents. Soit les deux allèles proviennent du même parent, soit chaque parent transmet un allèle. Il est alors possible de faire une liste de différents allèles et de noter ces deux cas. Le nombre d'allèles issus du même parent peut être modélisé par une variable aléatoire de loi binomiale[64]. Pour savoir s'il y a égale probabilité d'allèle de même provenance ou de provenance différente, on peut étudier un test statistique[64]. Inversement, pour simuler les allèles d'un individu, il est possible de simuler les fréquences des allèles par des variables aléatoires binomiales[65].
En linguistique, la loi binomiale est utilisée pour étudier la richesse du vocabulaire d'un texte[a 10]. C'est un outil quantitatif qui permet de mesurer la fréquence d'un mot dans un texte indépendamment de la longueur du texte. Plus précisément la méthode de Müller permet d'évaluer la richesse théorique du vocabulaire d'un texte grâce au vocabulaire d'un texte plus long, et ainsi comparer avec la richesse du vocabulaire du texte court en question. Techniquement, si est le nombre de mots d'un texte et celui d'un autre texte. Alors est la probabilité d'apparition d'un mot tiré au hasard dans le premier texte ; de même pour dans le deuxième texte[a 11]. Le nombre de mots ayant la même fréquence d'apparition dans le premier texte suit alors une loi binomiale de paramètres et p. Il est possible d'effectuer des tests statistiques pour conclure si la richesse du vocabulaire est grande ou non.
En 1908, Émile Borel étudie la fréquence des différents chiffres dans le développement décimal d'un nombre réel. Il considère les 2n premières valeurs de la décomposition décimale et estime la probabilité d'obtention du nombre de fois où apparaît chaque entier dans cette décomposition grâce à l'approximation par la loi normale. Il démontre ainsi le théorème des nombres normaux[a 12].
Une marche aléatoire sur est un processus stochastique à temps entier[66]. C'est-à-dire que la marche part d'une valeur initiale S0 = 0 par exemple et à chaque unité de temps, le marcheur se déplace (indépendamment du chemin parcouru avant) d'un pas vers le haut avec une probabilité p ou d'un pas vers le bas avec une probabilité 1 – p, ainsi S1 = –1 ou 1. Sn donne la position du marcheur au bout d'un temps n. Si p = 1 – p = 0,5, la marche est dite symétrique et le marcheur a autant de chance d'aller vers le haut que vers le bas. Dans ce cas, au bout du temps n, la variable aléatoire peut prendre comme valeurs et elle est de loi binomiale b(n, 0,5). Cette considération ainsi que la convergence vers la loi normale (voir ci-dessus) permet de démontrer qu'une marche aléatoire renormalisée converge vers le mouvement brownien (voir Théorème de Donsker)[67].
Notes et références[modifier | modifier le code]
- Gossett 2009, p. 310.
- Dodge 2007, p. 175.
- Dodge 2007, p. 287.
- Ruegg 1994, p. 38.
- Bogaert 2005, p. 50.
- Gossett 2009, p. 316.
- Ruegg 1994, p. 39.
- Gossett 2009, p. 311.
- Bogaert 2005, p. 305.
- Foata, Fuchs et Ranchi 2012, p. 68.
- Hald 2005, p. 5.
- Hald 2005, p. 485.
- Hazewinkel 1994, p. 438.
- Johnson, Kemp et Kotz 2005, p. 109.
- Johnson, Kemp et Kotz 2005, p. 136.
- Johnson, Kemp et Kotz 2005, p. 140.
- Gossett 2009, p. 274.
- Ruegg 1994, p. 23.
- Johnson, Kemp et Kotz 2005, p. 53.
- Dette et Studden 1997, p. 16.
- Johnson, Kemp et Kotz 2005, p. 110.
- Johnson, Kemp et Kotz 2005, p. 111.
- Hazewinkel 1994, p. 397.
- Courtin 2012, p. 1 G 17.
- Bogaert 2005, p. 329.
- Johnson, Kemp et Kotz 2005, p. 114.
- Mittag et Rinne 1993, p. 515.
- Mittag et Rinne 1993, p. 105.
- Johnson, Kemp et Kotz 2005, p. 115.
- Pfister 2012, p. 104.
- Courtin 2012, p. 1 G 16.
- Johnson, Kemp et Kotz 2005, p. 135.
- Johnson, Kemp et Kotz 2005, p. 116.
- Johnson, Kemp et Kotz 2005, p. 125.
- Lesigne 2005, p. 4ème couv.
- Bogaert 2005, p. 54.
- Johnson, Kemp et Kotz 2005, p. 218.
- Mittag et Rinne 1993, p. 109.
- Mittag et Rinne 1993, p. 116.
- Johnson, Kemp et Kotz 2005, p. 137.
- Johnson, Kemp et Kotz 2005, p. 253.
- Johnson, Kemp et Kotz 2005, p. 254.
- Courtin 2012, p. 1 G 18.
- Siegmund et Yakir 2007, p. 14.
- Foata, Fuchs et Ranchi 2012, p. 73.
- Hald 2005, p. 215.
- Johnson, Kemp et Kotz 2005, p. 121.
- Johnson, Kemp et Kotz 2005, p. 123.
- Bogaert 2005, p. 348.
- Mittag et Rinne 1993, p. 106.
- Hald 2005, p. 492.
- Ruegg 1994, p. 93.
- Hazewinkel 1994, p. 369.
- Johnson, Kemp et Kotz 2005, p. 118.
- Johnson, Kemp et Kotz 2005, p. 117.
- Lesigne 2005, p. 34.
- Bogaert 2005, p. 71.
- Dodge 2007, p. 288.
- Bogaert 2005, p. 349.
- Dagnelie 1998, p. 122.
- Dagnelie 1998, p. 76.
- Dagnelie 1998, p. 78.
- Siegmund et Yakir 2007, p. 17.
- Siegmund et Yakir 2007, p. 11.
- Siegmund et Yakir 2007, p. 240.
- Pfister 2012, p. 154.
- Pfister 2012, p. 155.
- Articles et autres sources
- Aimé Fuchs, « Plaidoyer pour la loi normale ».
- Suivre par exemple le lien en bas de cette page vers la leçon sur Wikiversité.
- (en) R. B. Potts (en), « Note on the factorial moments of standard distributions », Austr. J. Phys. (en), vol. 6, , p. 498 (lire en ligne).
- Marc Diener, « Probabilités élémentaires — Chap. 7 : Fonctions génératrices », sur Université Nice Sophia Antipolis, , p. 33.
- (en) V. Romanovsky, « Note on the moments of the binomial (p + q)n about its mean », Biometrika, vol. 15, nos 3-4, , p. 410-412 (DOI 10.2307/2331875).
- (en) Kais Hamza, « The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions », Statist. Probab. Lett., vol. 23, , p. 21-25 (lire en ligne).
- E. Morice, « Quelques modèles mathématiques de durée de vie », Revue de statistique appliquée, t. 14, no 1, , p. 45-126 (lire en ligne), p. 68.
- (en) Wassily Hoeffdin, « Probability inequalities for sums of bounded random variables », Journal of the American Statistical Association, vol. 58, no 301, , p. 13-30 (lire en ligne).
- (en) Victor Korolev et Irina Shevtsova, « An improvement of the Berry–Esseen inequality with applications to Poisson and mixed Poisson random sums », Scandinavian Actuarial Journal, vol. 2, , p. 81-105 (lire en ligne).
- Étienne Évrard, « Les mystères des vocables », Revue Informatique et Statistique dans les Sciences humaines - CIPL, vol. XXX (30 ?), nos 1 à 4, , p. 272-274 (lire en ligne).
- Étienne Brunet, « Müller le lexicomaître », CIPL, , p. 99-119 (lire en ligne).
- Émile Borel, « Les probabilités dénombrables et leurs applications arithmétiques », Rendiconti del Circolo Matematico di Palermo, Circolo Matematico di Palermo, vol. 27, no 1, , p. 247-271 (ISSN 0009-725X et 1973-4409, DOI 10.1007/BF03019651, lire en ligne).
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- Patrick Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, De Boeck Supérieur, , 402 p. (ISBN 2-8041-4794-0, lire en ligne)

- Jean-Pierre Courtin, L'Homme et les lois de la nature, vol. 1, Lulu.com, (ISBN 978-1-4710-3427-5, lire en ligne)

- Pierre Dagnelie, Statistique théorique et appliquée, vol. 2, Paris/Bruxelles, De Boeck Supérieur, , 659 p. (ISBN 2-8041-2802-4)

- (en) Holger Dette et William J. Studden, The Theory of Canonical Moments with Applications in Statistics, Probability, and Analysis, John Wiley & Sons, (lire en ligne)

- Yadolah Dodge, Statistique : Dictionnaire encyclopédique, Springer Science+Business Media, , 662 p. (ISBN 978-2-10-058102-3, lire en ligne)

- Dominique Foata, Aimé Fuchs et Jacques Ranchi, Calcul des probabilités : Cours, exercices et problèmes corrigés, Paris/Berlin/Heidelberg etc., Dunod, , 3e éd., 368 p. (ISBN 978-2-287-72093-2, lire en ligne)

- (en) Eric Gossett, Discrete Mathematics with Proof, Hoboken (N.J.), John Wiley & Sons, , 904 p. (ISBN 978-0-470-45793-1, lire en ligne)

- (en) Anders Hald, A History of Probability and Statistics and Their Applications before 1750, John Wiley & Sons, , 608 p. (ISBN 0-471-47129-1, lire en ligne)

- (en) Michiel Hazewinkel, Encyclopaedia of Mathematics (set), vol. 2, Dordrecht/Boston/London, Springer Science+Business Media, , 963 p. (ISBN 1-55608-010-7, lire en ligne)

- (en) Hans-Joachim Mittag et Horst Rinne, Statistical Methods of Quality Assurance, CRC Press, , 664 p. (ISBN 0-412-55980-3, lire en ligne)

- (en) Norman Johnson, Adrienne Kemp et Samuel Kotz, Univariate Discrete Distributions, John Wiley & Sons, , 646 p. (ISBN 0-471-27246-9, lire en ligne)

- (en) Emmanuel Lesigne, Heads or tails : an introduction to limit theorems in probability, Providence (R.I.), AMS, , 150 p. (ISBN 0-8218-3714-1, lire en ligne)

- Charles-Edouard Pfister, Théorie des probabilités : cours d'introduction avec application à la statistique mathématique, Lausanne, PPUR, , 229 p. (ISBN 978-2-88074-981-1, lire en ligne)

- Alan Ruegg, Probabilités et statistique, vol. 3, PPUR, , 153 p. (ISBN 2-88074-286-2, lire en ligne)

- (en) David Siegmund et Benjamin Yakir, The Statistics of Gene Mapping, Springer Science+Business Media, , 354 p. (lire en ligne)

Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Ressource relative à la santé :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- (en) Eric W. Weisstein, « Binomial Distribution », sur MathWorld


![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)























![{\displaystyle p\in [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91a2f4192860c4812bbe1c190645bfb14cc501ea)












































![{\displaystyle \mathbb {E} \left[{\frac {X}{n}}\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eee71355d341a5ba29d9c7e840187ed170e5fc39)

![{\displaystyle \mathbb {E} \left[\left({\frac {X}{n}}-p\right)^{2}\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6cdd201f2e428f79c0d7abc69bd1e4e237b29f1)

![{\displaystyle \mathbb {E} \left[\left({\frac {X}{n}}-p\right)^{4}\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cbf817869a6c33fe63aa98c16b87bd41c66f929)





























![{\displaystyle F(x)=\mathbb {P} (X\leq x)={\begin{cases}1&{\textrm {si}}\;x\geq n\\[4pt]\displaystyle \sum _{k=0}^{\lfloor x\rfloor }{n \choose k}p^{k}(1-p)^{n-k}&{\textrm {si}}\;0\leq x<n\\[4pt]0&{\textrm {si}}\;x<0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36d54d49da9718a1bbbc042fff9808d76b48fd97)







![{\displaystyle \ln \left(\mathbb {E} \left[(1+t)^{X}\right]\right)=n\ln \left(1+pt\right)\;,\;\forall t\in \mathbb {R} _{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f25021966961f5b80ce35db55d631ad6b6834dde)










![{\displaystyle ]n-r_{2},n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db4317c03f64d6e30836c3bbba4dd6a1522c1afc)












![{\displaystyle p'\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34b2d2bf6fb3d5532c750b1e4bdfde5548138cd7)


















































































