Loi de Burr

Loi de Burr
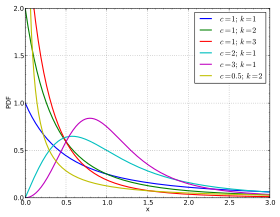Densité de probabilité
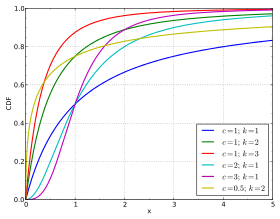Fonction de répartition
Paramètres	$c>0\!$ $k>0\!$
Support	$x>0\!$
Densité de probabilité	$ck{\frac {x^{c-1}}{(1+x^{c})^{k+1}}}\!$
Fonction de répartition	$1-\left(1+x^{c}\right)^{-k}$
Espérance	$k\operatorname {B} (k-1/c,\,1+1/c)$ où B est la fonction bêta
Médiane	$\left(2^{\frac {1}{k}}-1\right)^{\frac {1}{c}}$
Mode	$\left({\frac {c-1}{kc+1}}\right)^{\frac {1}{c}}$

En théorie des probabilités, en statistique et en économétrie, la loi de Burr, loi de Burr de type XII, loi de Singh-Maddala, ou encore loi log-logistisque généralisée est une loi de probabilité continue dépendant de deux paramètres réels positifs c et k. Elle est communément utilisée pour étudier les revenus des ménages.

Si X suit une loi de Burr (ou Singh-Maddala), on notera $X\sim SM(c,k)$.

Caractérisation

La densité de probabilité de la loi de Burr est donnée par :

$f(x;c,k)={\begin{cases}ck{\frac {x^{c-1}}{(1+x^{c})^{k+1}}}&{\text{ si }}x>0\\0&{\text{ sinon}}\end{cases}}$

et sa fonction de répartition est :

$F(x;c,k)={\begin{cases}1-\left(1+x^{c}\right)^{-k}&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}$

Lien avec d'autres distributions

• Si $c=1$, la loi de Burr est la Distribution de Pareto.
• Si $k=1$, la loi de Burr est la loi log-logistique.
• Si $k\to +\infty$, la loi de Burr est la loi de Weibull.

Références

• (en) I. W. Burr, « Cumulative frequency functions », Annals of Mathematical Statistics, vol. 13, n^o 2,‎ 1942, p. 215–232 (DOI 10.1214/aoms/1177731607, lire en ligne).
• (en) R. N. Rodriguez, « A guide to Burr Type XII distributions », Biometrika, vol. 64,‎ 1977, p. 129–134

Voir également

Articles connexes

• loi de Dagum, également connue comme la loi de Burr inversée.
• Système de Burr, qui répertorie les autres types de lois de Burr