Loi bêta décentrée

Loi bêta décentrée
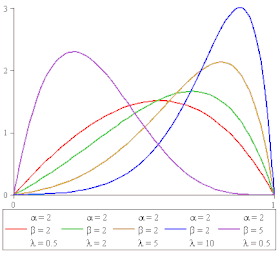Densité de probabilité
Fonction de répartition
Paramètres	$\alpha >0$ et $\beta >0$, paramètres de forme $\lambda \in \mathbb {R}$, paramètre de décentralisation
Support	$x\in [0;1]\!$
Densité de probabilité	$\scriptstyle \sum _{j=0}^{\infty }{\frac {1}{j!}}\left({\frac {\lambda }{2}}\right)^{j}\mathrm {e} ^{-\lambda /2}{\frac {x^{\alpha +j-1}(1-x)^{\beta -1}}{B(\alpha +j,\beta )}}$
Fonction de répartition	$\scriptstyle \sum _{j=0}^{\infty }{\frac {1}{j!}}\left({\frac {\lambda }{2}}\right)^{j}\mathrm {e} ^{-\lambda /2}I_{x}(a+j,b)$

En théorie des probabilités et en statistique, la loi bêta décentrée est une loi de probabilité continue généralisant la loi bêta (sous-entendue centrée) en la décentrant grâce à un paramètre $\lambda$, c'est-à-dire en décalant sa moyenne.

Densité de probabilité

La densité de probabilité de la loi bêta décentrée est :

$f(x)={\begin{cases}\displaystyle \sum _{j=0}^{\infty }{\frac {1}{j!}}\left({\frac {\lambda }{2}}\right)^{j}\mathrm {e} ^{-\lambda /2}{\frac {x^{\alpha +j-1}(1-x)^{\beta -1}}{B(\alpha +j,\beta )}}&{\hbox{ pour }}x\in [0,1]\\0&{\hbox{ sinon }}\end{cases}}$

où $B$ est la fonction bêta, $\alpha$ et $\beta$ sont les paramètres de forme et $\lambda$ est le paramètre de décentrement.

Fonction de répartition

La fonction de répartition de la loi bêta décentrée est :

$F(x)=\sum _{j=0}^{\infty }{\frac {1}{j!}}\left({\frac {\lambda }{2}}\right)^{j}\mathrm {e} ^{-\lambda /2}I_{x}(a+j,b)$

où $I_{x}$ est la fonction bêta incomplète régularisée, $a$ et $b$ sont les paramètres de forme et $\lambda$ est le paramètre de décentrement.

Cas particuliers

Quand $\lambda =0$, la loi bêta décentrée est la loi bêta.

Références

• (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne)
• (en) J.L. Jr Hodges, « On the noncentral beta-distribution », Annals of Mathematical Statistics, vol. 26,‎ 1955, p. 648–653
• (en) G.A.F. Seber, « The non-central chi-squared and beta distributions », Biometrika, vol. 50,‎ 1963, p. 542–544