Loi de Laplace (probabilités)

Laplace
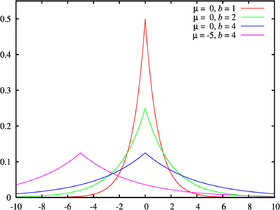Densité de probabilité


Fonction de répartition

Paramètres	$\mu \,$ Paramètre de position (réel) $b>0\,$ Paramètre d'échelle (réel)
Support	$x\in (-\infty ;+\infty )\,$
Densité de probabilité	${\frac {1}{2\,b}}\exp \left(-{\frac {\|x-\mu \|}{b}}\right)\,$
Fonction de répartition	voir plus bas
Espérance	$\mu \,$
Médiane	$\mu \,$
Mode	$\mu \,$
Variance	$2\,b^{2}$
Asymétrie	$0\,$
Kurtosis normalisé	$3$
Entropie	$\log _{2}(2{\rm {e}}b)$
Fonction génératrice des moments	${\frac {\exp(\mu \,t)}{1-b^{2}\,t^{2}}}\,\!$ pour $\|t\|<1/b\,$
Fonction caractéristique	${\frac {\exp({\rm {i}}\,\mu \,t)}{1+b^{2}\,t^{2}}}\,\!$
modifier

En théorie des probabilités et en statistiques, la loi (distribution) de Laplace est une densité de probabilité continue, portant le nom de Pierre-Simon de Laplace. On la connaît aussi sous le nom de loi double exponentielle, car sa densité peut être vue comme l'association des densités de deux lois exponentielles, accolées dos à dos. La loi de Laplace s'obtient aussi comme résultat de la différence de deux variables exponentielles indépendantes.

Caractérisation[modifier | modifier le code]

Densité de probabilité[modifier | modifier le code]

Une variable aléatoire suit une loi de Laplace(μ, b) si sa densité de probabilité est

f(x|\mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,\!

={\frac {1}{2b}}{\begin{cases}\exp \left(-{\frac {\mu -x}{b}}\right)&{\mbox{si }}x<\mu \\[8pt]\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{si }}x\geq \mu \end{cases}}

Le réel μ est un paramètre de position et b > 0 un paramètre d'échelle. Si μ = 0 et b = 1, la loi de Laplace est dite standard et sa restriction à la demi-droite réelle positive est la loi exponentielle de paramètre 1/2.

La densité rappelle aussi celle de la loi normale ; toutefois, tandis que la loi normale est exprimée en termes de la différence au carré $(x-\mu )^{2}$ , la loi de Laplace fait intervenir la différence absolue $|x-\mu |$ . La loi de Laplace présente alors des queues plus épaisses que la loi normale.

Fonction de répartition[modifier | modifier le code]

La densité de la loi de Laplace s'intègre aisément grâce à la présence de la valeur absolue. Sa fonction de répartition est :

$F(x)\,$	$=\int _{-\infty }^{x}\!\!f(u)\,\mathrm {d} u$
	$={\begin{cases}{\frac {1}{2}}\exp \left(-{\frac {\mu -x}{b}}\right)&{\mbox{si }}x<\mu \\[8pt]1-{\frac {1}{2}}\exp \left(-{\frac {x-\mu }{b}}\right)&{\mbox{si }}x\geq \mu \end{cases}}$
	$=0,5\,[1+\operatorname {sgn}(x-\mu )\,(1-\exp(-\|x-\mu \|/b))].$

La réciproque de la fonction de répartition est

F^{-1}(p)=\mu -b\,\operatorname {sgn}(p-0,5)\,\ln(1-2|p-0,5|).

Tirer une variable selon la loi de Laplace[modifier | modifier le code]

Étant donné une variable U, tirée selon une loi uniforme continue dans l'intervalle [-1/2, 1/2], la variable suivante

X=\mu -b\,\operatorname {sgn}(U)\,\ln(1-2|U|)

est distribuée selon la loi de Laplace de paramètres μ et b. Ce résultat provient de l'expression de l'inverse de la fonction de répartition et de la méthode de la transformée inverse.

Une variable Laplace(0, b) peut aussi se générer comme la différence de deux variables exponentielles, de paramètre 1/b, indépendantes. De même, une loi Laplace(0, 1) peut s'obtenir en considérant le logarithme du ratio de deux variables uniformes indépendantes.

Estimation des paramètres[modifier | modifier le code]

Étant donné un échantillon de N variables iid x₁, x₂..., x_N, un estimateur ${\hat {\mu }}$ de $\mu$ est la médiane empirique^[1], et un estimateur par maximum de vraisemblance de b est

{\hat {b}}={\frac {1}{N}}\sum _{i=1}^{N}|x_{i}-{\hat {\mu }}|.

Moments[modifier | modifier le code]

Les moments centrés d'ordre r peuvent s'exprimer à partir des moments ordinaires :

\mu _{r}'={\frac {1}{2}}\sum _{k=0}^{r}{\binom {r}{k}}k!b^{k}\mu ^{(r-k)}\{1+(-1)^{k}\}

Lois associées[modifier | modifier le code]

Si $X\sim \mathrm {Laplace} (0,b)\,$ alors $|X|\sim \mathrm {Exponentielle} (b^{-1})\,$ est une loi exponentielle;
Si $X\sim \mathrm {Exponentielle} (\lambda )\,$ et Y indépendante de $X\,$ suit une loi de Rademacher, alors $XY\sim \mathrm {Laplace} (0,\lambda ^{-1})\,$ ;
Si $X_{1}\sim \mathrm {Exponentielle} (\lambda _{1})\,$ et $X_{2}\sim \mathrm {Exponentielle} (\lambda _{2})\,$ indépendantes de $X_{1}\,$ , alors $\lambda _{1}X_{1}-\lambda _{2}X_{2}\sim \mathrm {Laplace} \left(0,1\right)\,$ .

Notes et références[modifier | modifier le code]

↑ Robert M. Norton, « The Double Exponential Distribution: Using Calculus to Find a Maximum Likelihood Estimator », The American Statistician, vol. 38, n^o 2,‎ mai 1984, p. 135–136 (DOI 10.2307/2683252, lire en ligne)

Portail des probabilités et de la statistique

[1] Robert M. Norton, « The Double Exponential Distribution: Using Calculus to Find a Maximum Likelihood Estimator », The American Statistician, vol. 38, n^o 2,‎ mai 1984, p. 135–136 (DOI 10.2307/2683252, lire en ligne)

[1]