Pile ou face

Le pile ou face est un jeu de hasard se jouant avec une pièce de monnaie. Le principe du jeu est de lancer en l'air une pièce équilibrée et de parier sur le côté sorti. La pièce tournoyante tombe au sol et s'y stabilise, ou bien elle est rattrapée d'une main et posée à plat dans l'autre main.
L'origine du nom « pile ou face » vient des noms des deux côtés d'une pièce de monnaie[note 1].
La première utilisation de ce jeu sous cette forme date de la création de la monnaie métallique. Cependant, d'autres formes existaient précédemment en utilisant des objets possédant deux côtés distincts, un coquillage par exemple. Le but est de faire un choix binaire au hasard. Aujourd'hui encore, jouer à « pile ou face » signifie qu'on laisse une décision se prendre au hasard, en fonction du côté de la pièce qui apparaîtra après le lancer.
Le jeu de pile ou face est toujours utilisé en sport par exemple. Il sert de support à beaucoup de problèmes en probabilité, certains restent encore ouverts comme le problème de la Belle au bois dormant.
C'est un outil important dans la théorie des jeux ainsi que dans la théorie des probabilités.
Origine[modifier | modifier le code]

« Tête » (de Janus) ou « Navire » ?



Des écrits anciens nomment un jeu d'enfants de la Grèce antique, l'Ostrakinda, où le choix du rôle des deux équipes est fait en jetant une coquille ou un tesson de jarre, blanc d'un côté, noir de l'autre et en criant « nuit ou jour »[1],[2],[3]. Autour du IVe siècle av. J.-C., il y a une grande variété de monnaies, chaque cité possédant un signe distinctif sur le côté face : une chouette pour Athènes, une tortue pour Égine, un crabe pour Agrigente, etc. Sur le côté pile, des portraits de Dieux ou de souverains commencent à apparaitre[4].
Dans l'Antiquité romaine, à partir du IIIe siècle av. J.-C., les gravures que l'on trouvait sur les pièces de monnaie (as romain ou livre romaine) représentaient le visage (double visage) de Janus sur un côté de la pièce, et le navire qui l'avait amené en Italie sur l'autre. L'expression « capita aut navia » (« tête ou navire » en latin) était alors usitée[3]. Il existe également plusieurs autres représentations : Dieux, monuments, souverains, etc[4].
En 781, Charlemagne établit une réforme monétaire qui interdit l'utilisation des anciennes monnaies. Des nouvelles pièces sont alors frappées avec son monogramme (en forme de croix) sur le revers et une légende circulaire autour d'une croix sur l'avers[5]. Le revers s'appelant pile, on disait alors, s'agissant d'un choix au hasard, « croix ou pile ». « Croix ou pile » est encore employé au XVIIe siècle, par le chirurgien et flibustier Alexandre-Olivier Exquemelin dans son Journal de bord, s'agissant alors des « perulero » les pièces de 8 de l'Empire espagnol frappées au Pérou, où la croix d'Espagne figure à l'avers et les colonnes d'Hercule au revers[6]. L'expression se rencontre également plus tard en 1856 dans Le Père Goriot d'Honoré de Balzac au sujet d'un duel [7]. L'origine du terme pile reste incertaine, voir l'article Revers (numismatique) pour plus de détails. Plus tard, le fils de Charlemagne, Louis le Pieux, refit apparaître une monnaie à son effigie[5].
À partir du début de la renaissance, grâce à une ordonnance[8] d'Henri II du 31 janvier 1548, les souverains profitent du renouveau artistique pour faire représenter leur portrait de manière ressemblante et valorisante[4]. Le côté face est donc le côté où était inscrit sur la pièce de monnaie le visage du roi, du prince, de l'empereur, ou une allégorie (Marianne, la semeuse). Ainsi, lors de la fuite manquée de Louis XVI en 1791, à Varennes, il aurait été reconnu par le maître poste grâce à l’effigie royale sur le côté face d’un écu[9].
En langage numismatique, pile se nomme le revers et face l'avers. Aujourd'hui, le côté pile est celui qui indique la valeur de la pièce de monnaie. Dans les pièces de l'Union européenne, le côté pile est le côté des pièces portant les chiffres 1 (centime), 2 (centimes), 5 (centimes), 10 (centimes), 20 (centimes), 50 (centimes), 1 (euro) ou 2 (euros). Pour le côté face, les pièces françaises de 1, 2 et 5 centimes sont illustrées d'une représentation de Marianne ; les pièces de 10, 20 et 50 centimes représentent la semeuse, alors qu'un arbre est représenté sur les pièces de 1 et 2 euros. Certains pays européens ont choisi de faire figurer des visages sur les pièces de 1 et 2 euros.
Il existe également des pièces de monnaie dont les deux côtés sont identiques : deux face ou deux pile. Elles peuvent être de vraies pièces issues d'une erreur de fabrication[10],[11], dans ce cas elles prennent une grande valeur notamment pour les collectionneurs. La pièce possède alors un côté avers et un revers, sans possibilité de distinction. Cependant beaucoup de ces doubles pièces sont de fausses pièces.
La notion étymologique de « pile ou face » et le jeu de « pile ou face » existent également dans d'autres langues. Certaines langues possèdent des termes différents pour la notion et pour le jeu. Voici une liste, non exhaustive.
| Langue | Dénomination | Signification | |
|---|---|---|---|
| Jeu | Notion | ||
| (de) Allemand | Münzwurf | Kopf oder Zahl | tête ou nombre |
| (en) Anglais | Coin flipping | Heads or Tails | tête ou queue |
| (ar) Arabe (Liban) | طرة و نقشة | أرز أو شختور | cèdre ou bateau |
| (ar) Arabe (Maroc) | نجمة ولا راس | نجمة أو رأس | étoile ou tête |
| (ca) Catalan | Cara o creu | face ou croix | |
| (es) Espagnol | Cara o cruz | face ou croix | |
| (ga) Gaélique | Ceann nó Cláirseach | tête ou harpe | |
| (el) Grec | Κορώνα γράμματα | couronne ou lettres | |
| (he) Hébreu | הטלת מטבע | עץ או פלי | arbre ou Palestine (pali comme raccourci de Palestine) |
| (hu) Hongrois | Fej vagy írás | tête ou écriture | |
| (it) Italien | Testa o croce | tête ou croix | |
| (ja) Japonais | コイントス (koin tosu) |
||
| (lv) Letton | Cipars vai ģerbonis | nombre ou blason | |
| (es) Mexicain | Aguila o sol | aigle ou soleil | |
| (nl) Néerlandais | Tossen | Kruis of munt | tête ou nombre |
| (no) Norvégien | krone eller mynt | couronne ou pièce | |
| (oc) Occitan | Crotz e piela / Testa ò crotz | croix et pile / tête ou croix | |
| (pt) Portugais | Cara ou coroa | face ou couronne | |
| (ro) Roumain | Cap sau pajură | tête ou aigle | |
| (ru) Russe | Орлянка (Orlianka) |
Орёл или ре́шка (Oriol ili réchka) |
aigle ou visage (étymologie douteuse) |
| (sv) Suédois | Krona eller klave | couronne ou blason | |
| (tr) Turc | Yazı Tura | écriture ou face | |
| (vi) Vietnamien | ngửa hay sấp | face ou revers | |
-
L'aigle et le soleil sur un peso mexicain de 1908.
-
Couronne sur un réal portugais de 1909.
-
Aigle sur un rouble russe de 1998.
Utilisation[modifier | modifier le code]
Procédure[modifier | modifier le code]
Le jeu de pile ou face permet d'aider à la décision d'un choix binaire. La méthode la plus courante pour lancer une pièce est de positionner horizontalement sur le bout du pouce et la tranche de l'index[12]. Il suffit alors d'exercer une extension du pouce afin de donner un mouvement de rotation à la pièce[note 2], la pièce doit réaliser au moins une rotation entière en l'air[13]. D'après une étude statistique[14], le nombre moyen de retournements de pièce pour un pile ou face typique est de 19. On laisse la pièce retomber au sol ou alors on la rattrape et la positionne horizontalement sur le dos de l'autre main. Dans tous les cas c'est le côté supérieur de la pièce qui donne le résultat.
Il est courant de parier sur pile ou sur face avant le lancer de pièce. On peut également parier pendant que la pièce est en l'air, ce qui évite toute tentative de tricherie de la part du lanceur.
Pile ou face par téléphone[modifier | modifier le code]
Jouer à pile ou face par téléphone est a priori impossible car seule la personne qui lance la pièce voit le résultat du lancer, et peut donc mentir sur son résultat. Il est cependant possible de concevoir une procédure pour jouer équitablement par téléphone, en utilisant une fonction de hachage . La fonction de hachage utilisée doit être telle qu'il n'est pas envisageable à partir d'un haché de calculer un antécédent tel que ; et telle qu'il ne soit pas non plus envisageable de déterminer une collision, c'est-à-dire deux entrées distinctes et vérifiant [15]. SHA-256 est un exemple de fonction de hachage pouvant être utilisée[note 3].
Supposons qu'Alice et Bob veulent jouer à pile ou face équitablement par téléphone[15] :
- Alice choisit aléatoirement un nombre de grande taille , calcule et le met en gage en envoyant le résultat à Bob[note 4];
- Bob lance une pièce et annonce le résultat à Alice : Pile (0) ou Face (1) ;
- Alice révèle alors : si le bit de poids fort[note 5] est égal au résultat du lancer Bob gagne, sinon c'est Alice.
La robustesse du protocole repose sur le fait qu'Alice est obligée de s'engager sur Pile (0) ou sur Face (1) avant le lancer de la pièce et sans que Bob ne connaisse la valeur de cet engagement[15]. Pour Alice cela suppose que l'on ne puisse pas trouver deux nombres dont les bits de poids fort soient différents mais dont le haché soit identique, ce qui donnerait l'illusion qu'Alice s'est engagée sur le choix (0) ou sur le choix (1) selon sa convenance[15]. Pour Bob cela suppose que l'on ne peut pas déduire à partir de [15].
Une autre manière de procéder est d'utiliser une source de hasard publique, infalsifiable et contrôlable, comme par exemple la parité du chiffre des dixièmes de la température relevée par Météo France sur un lieu et à une date données[16].
Générateurs en ligne de pile ou face[modifier | modifier le code]
Avec le développement de la technologie numérique et de l'internet, la méthode traditionnelle de lancer une pièce pour obtenir "pile" ou "face" a été complétée par l'utilisation de générateurs en ligne[17]. Ces outils numériques, disponibles sur de nombreux sites web et applications, fournissent un résultat aléatoire équivalent à un véritable lancer de pièce.
Le fonctionnement de ces générateurs repose généralement sur un algorithme de génération de nombres aléatoires. Lorsqu'un utilisateur sollicite un lancer de pile ou face, l'algorithme génère un nombre aléatoire qui détermine si le résultat sera "pile" ou "face". Ce processus est conçu pour être équitable, avec une probabilité de 50% pour chaque issue, à l'instar d'un lancer de pièce physique.
Ces générateurs en ligne de pile ou face ont trouvé de nombreux usages, surtout là où un lancer de pièce physique serait difficile ou peu pratique. Ils sont particulièrement utiles pour les prises de décision à distance ou les votes en ligne. De plus, ils peuvent être utilisés dans des situations où la transparence est nécessaire, car le résultat du lancer peut être vérifié par toutes les parties impliquées.
Toutefois, bien que ces outils soient conçus pour être justes et impartiaux, il est toujours important d'évaluer la fiabilité du générateur de pile ou face en ligne avant de l'utiliser pour des décisions importantes. Des sites et applications de confiance utilisent des algorithmes vérifiés pour assurer l'équité et l'aléatoire du résultat.
En sport[modifier | modifier le code]
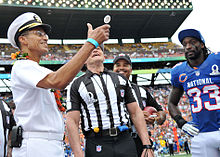
Dans plusieurs sports tels que le badminton, le cricket, le football américain, le handball, ou encore le rugby à XV, avant le coup d'envoi d'une partie, l'équipe gagnante au pile ou face peut choisir l'équipe qui engage ou le côté du terrain. Le tirage au sort par pile ou face peut également servir à déterminer un vainqueur ou un qualifié, lorsque toutes les possibilités de départage (comme rejouer un match par exemple) ou autres critères (comme la différence de buts, etc.) prévus par le règlement ont été épuisés et n'ont pas permis de séparer les équipes à égalité.
En 1919, le premier président du club de football espagnol Valence CF a été choisi au jeu de pile ou face. Après 7 h 35 d'un match de ping-pong, Marin Goldberger a été désigné vainqueur par un pile ou face au championnat du monde en 1936. De 1966 à 1985, lors de la Draft de la NBA, les équipes de basket-ball utilisent des jeux de pile ou face pour l'obtention du premier choix de joueur.
En football, avant l'introduction de la règle des tirs au but au début des années 1970, il n'était pas rare de voir des qualifications se décider à la « pièce » lors de rencontres à élimination directe. En 1963, lors des huitièmes de finale de la coupe des clubs champions disputés en matchs aller-retour, les équipes du Galatasaray et du FC Zurich, après avoir chacune remporté sur le même score son match à domicile, s'affrontent en match d'appui et terminent à égalité à la fin de la prolongation : le FC Zurich se qualifie au pile ou face. En demi-finale de la coupe de France de 1967, après trois matchs nuls après prolongation entre les équipes de Lyon et d'Angoulême, le nombre maximum de matchs rejoués prévu par le règlement étant atteint, c'est à pile ou face que les Lyonnais obtiennent leur qualification. À l'échelon des compétitions majeurs internationales, la Turquie obtient notamment sa qualification pour la Coupe du monde 1954 à pile ou face aux dépens de l'Espagne. En demi-finale du Championnat d'Europe 1968, l'Italie, à domicile, obtient sa qualification pour la finale à pile ou face après un match nul après prolongation contre l'URSS.
Jeux[modifier | modifier le code]
Jeux avec mise[modifier | modifier le code]
On peut jouer au pile ou face en pariant sur une mise, jeu souvent présent dans les exercices de probabilité. L'étude se porte alors sur des lancers indépendants simultanés ou successifs. Plusieurs règles et stratégies de mises existent.
On considère un jeu de pile ou face classique : un joueur mise une somme sur pile ou face, s'il obtient le bon résultat il gagne une fois sa mise (en plus de sa mise), sinon il perd sa mise. On recommence alors un autre lancer de pièce. Il existe une stratégie permettant au joueur d'être toujours gagnant à la longue : le joueur mise 1 euro pour le premier tirage. S'il perd, il mise 2 euros au deuxième lancer, s'il perd, il mise 4 euros au troisième lancer, et ainsi de suite. S'il n'a toujours pas gagné, il mise 2n-1 au n-ième lancer. Le joueur arrête de jouer lorsqu'il gagne.
Ce jeu est gagnant pour le joueur. En effet, S'il gagne au n-ième lancer, il aura misé euros et aura gagné 2n euros. Son gain est donc de 1 euro. De plus le jeu se termine en temps fini. La limite d'utilisation de cette technique est que le jeu n'est pas borné en temps, c'est-à-dire qu'il peut durer très longtemps. Pour être gagnant, il faut ainsi supposer que le joueur ait un porte-monnaie infini, c'est-à-dire qu'il peut miser 2n même pour n grand.
Jeux sans mise[modifier | modifier le code]
Certains jeux utilisent la notion de hasard binaire (oui/non, accepté/refusé, gagnant/perdant par exemple) pendant leur déroulement. Ce sont généralement des jeux de rôle dans lesquels des actions ou évènements sont laissés au hasard d'un jeu de pile ou face. Citons par exemple le jeu Magic : l'assemblée dans lequel certaines cartes demandent la réalisation d'un jeu de pile ou face[18].
Pour les choix multiples (supérieurs à trois possibilités), des dés multifaces sont généralement utilisés (1d6 signifie jeter un dé à six côtés). 1d2 signifie donc faire un jeu de pile ou face. Certains « dés à deux côtés » ont alors la forme d'une pièce[19].
Citons, par exemple, le jeu Prince Valiant qui n'utilise que des pièces.
Exemples de jeux[modifier | modifier le code]
Les pièces sont considérées équilibrées.
- Jeu pour deux joueurs et un lancer (jeu classique)
- Un joueur choisit pile, l'autre face. La pièce est jetée en l'air. Le joueur ayant choisi le bon côté de la pièce gagne, l'autre perd. Le jeu est équilibré, les joueurs ont même probabilité de gagner.
- Jeu pour deux joueurs et deux lancers
- Un joueur choisit identiques, l'autre différents. Les deux pièces sont jetées en l'air (ou deux fois la même pièce). Si les deux pièces donnent le même résultat, le joueur ayant choisi identiques gagne, l'autre perd. Si les deux pièces donnent des résultats différents, le joueur ayant choisi différents gagne, l'autre perd. Le jeu est équilibré.
- Jeu pour deux joueurs et n lancers
- Un nombre impair n est choisi en début de jeu, ce choix n'influencera pas les chances de gagner. Un joueur choisit pile, l'autre face. Une pièce est jetée en l'air n fois. Si pile est apparu plus de fois, le joueur ayant choisi pile gagne, l'autre perd. De même pour face. Le jeu est équilibré.
- Jeu pour deux joueurs (un joueur et une banque) et un nombre indéterminé de lancers (paradoxe de Saint-Petersbourg)
- Un joueur et une banque, le joueur donne sa mise à la banque, on lance en l'air une pièce de monnaie. Si face apparaît, la banque paie 1 euro au joueur, et on arrête le jeu. Si face apparaît seulement au second lancé, la banque paie 2 euros, et on arrête le jeu. Sinon, on relance la pièce. Si face apparaît seulement au troisième lancer, la banque paie 4 euros au joueur. Si face apparaît pour la première fois au n-ième lancer, la banque paie 2n-1 euros au joueur et on arrête le jeu. Existe-t-il une mise initiale du joueur pour que le jeu soit équitable, c'est-à-dire pour que ni la banque ni le joueur ne soient avantagés? Contre-intuitivement, le joueur garde l'avantage quelle que soit sa mise!
- Jeu pour deux joueurs et une pièce (problème du chevalier de Méré ou problème des partis)
- Un joueur choisit pile, l'autre face. La pièce est lancée en l'air un certain nombre de fois. Le joueur ayant choisi pile gagne si pile apparait trois fois avant que face n'apparaisse trois fois. De même pour face. Le nombre 3 peut être modifié sans changer les chances de gagner. Le nombre de lancers n'est pas fixe mais le jeu s'arrêtera en temps fini. Le jeu est équilibré.
Si on stoppe le jeu avant la fin, les deux joueurs se répartissent la mise du jeu. Mais quelle est la part de chacun en fonction du nombre de pile et face déjà apparus ? Pascal a donné une solution par un raisonnement de proche en proche (en utilisant notamment le triangle de Pascal), Fermat a donné la même solution par un raisonnement différent (utilisant des évènements équiprobables)[20].
- Jeu pour trois joueurs et trois pièces (l'intrus)
- Chaque joueur jette sa pièce en l'air. Si tous les résultats sont les mêmes, on recommence. Sinon, un joueur a obtenu un résultat différent des deux autres, ce joueur gagne. Le nombre de lancers n'est pas fixe mais le jeu s'arrêtera en temps fini. Le jeu est équilibré.
- Jeu pour n joueurs et n pièces
- Chaque joueur jette sa pièce en l'air. S'il n'y a pas de résultat (pile ou face) majoritaire, on recommence. Sinon, les joueurs en nombre majoritaire sont éliminés du jeu. On recommence avec les joueurs restants jusqu'à obtention de un ou deux joueurs restants. S'il reste un joueur, il est gagnant ; s'il reste deux joueurs, ils jouent à un jeu de pile ou face classique. Le nombre de lancers n'est pas fixe mais le jeu s'arrêtera en temps fini. Le jeu est équilibré.
Concept et anecdotes[modifier | modifier le code]

L'idée du jeu de pile ou face, c'est-à-dire d'une expérience aléatoire dont le résultat est un succès ou un échec, permet d'illustrer le concept d'un choix aléatoire. Blaise Pascal, dans ses Pensées, utilise la métaphore du jeu de pile ou face pour illustrer son fameux pari :
« Examinons donc ce point et disons : Dieu est, ou il n’est pas. Mais de quel côté pencherons-nous ? La raison n’y peut rien déterminer. Il y a un chaos infini qui nous sépare. Il se joue un jeu, à l’extrémité de cette distance infinie, où il arrivera croix ou pile : que gagerez-vous ? [...] Pesons le gain et la perte, en prenant croix que Dieu est. Estimons ces deux cas : si vous gagnez, vous gagnez tout ; si vous perdez, vous ne perdez rien. Gagez donc qu’il est sans hésiter ! »
Le jeu de pile ou face est utilisé pour consulter le système de divination Yi Jing. La valeur 2 est assignée à pile et 3 à face[22], on effectue alors la somme des résultats sur trois lancers de pièce. Dans un domaine plus scientifique, les différents pas d'une marche aléatoire sont donnés par le résultat d'un jeu de pile ou face. Il est utilisé comme métaphore en mécanique quantique : le résultat de l'expérience du chat de Schrödinger est déterminé par « un jeu de pile ou face dont le résultat est inconnu avant l'ouverture de la boîte »[23].
En 1851, un pile ou face détermine si une nouvelle ville dans l'Oregon sera nommée d'après Boston ou Portland, Portland gagne.
En 1939, Bill Hewlett et Dave Packard ont parié à pile ou face si leur société allait s’appeler Hewlett-Packard ou Packard-Hewlett[24].
Le soir de leur passage au Monterey Pop Festival en 1967, pour savoir qui des Who ou de The Jimi Hendrix Experience passerait avant l'autre, il fallut tirer à pile ou face, et les Who gagnèrent.
En 1968, Roland Moreno invente une machine à tirer à pile ou face, la « Matapof »[25].
En 1970, l'éleveur Ogden Phipps et le couple Christopher et Penny Chenery jouent à pile ou face le droit de choisir un des trois poulains de l'étalon Bold Ruler. Les perdants au jeu deviendront propriétaires d'un des plus grands champions de l'histoire des courses : le pur-sang anglais Secretariat.
En 1987, Corynne Charby interpréta la chanson « Pile ou face » composée par Franck Yvi et Jean-Louis D'Onorio. Cette chanson fut reprise par Emmanuelle Béart en 2002 dans le film Huit femmes de François Ozon. Le thème de la chanson est de « vivre sa vie à pile ou face », c'est-à-dire de laisser le hasard décider.
En 2007, un juge américain a été destitué après avoir décidé à pile ou face qui, du père ou de la mère, avait le droit de passer Noël avec leur enfant[26].
Le guide des circonscriptions du parti démocrate de l'Iowa prévoit que lorsqu'il y a égalité entre deux candidats, le choix devait être fait au pile ou face. Cette situation est apparue six fois en 2016 lors de la primaire de l'élection présidentielle[27].
En fiction[modifier | modifier le code]
Certains personnages de film sont associés au jeu du pile ou face, ce dernier devenant parfois même l'identité du personnage. Dans le film américain Scarface, sorti en 1932 et réalisé par Howard Hawks, le personnage Guino Rinaldo, joué par George Raft, est un gangster jouant constamment à pile ou face. Ce personnage fut parodié par Bugs Bunny dans le dessin animé Racketeer Rabbit en 1946. George Raft parodia son propre personnage dans la comédie Certains l'aiment chaud de Billy Wilder, avec le personnage de Spats Colombo. Spats rencontre un gangster rival jouant à pile ou face, il lui demande « Où as-tu appris à faire ça ? »[28],[29]. Le personnage schizophrène Double-Face ou Pile-ou-face ennemi de Batman créé en 1942 par Bob Kane et Bill Finger décide de la légalité de ses crimes par un jeu de pile ou face. Il utilise une pièce à deux côtés identiques à l'exception d'une rayure de couteau sur l'une d'elles. C'est une pièce de dollar en argent. Citons également le roman Non, ce pays n'est pas pour le vieil homme et son adaptation cinématographique, No Country for Old Men sorti en 2007 de Joel et Ethan Coen, où le tueur à gage psychopathe Anton Chigurh, utilise un lancer de pièce et laisse la destinée décider de la vie de ses victimes[30]. Une parodie a été faite dans l'épisode 19 de la vingtième saison des Simpson, Une adresse chic[31].
Le jeu de pile ou face est également à l'origine de certaines intrigues fictives. À la fin de la nouvelle d'Isaac Asimov La Machine qui gagna la guerre publiée en 1961, le personnage de Lamar Swift révèle à ses collaborateurs que l'ordinateur ne donnait en fait pas toutes les informations et qu'il jouait les grandes décisions à pile ou face. Dans l'épisode 16 de la deuxième saison de la série télévisée La Quatrième Dimension, le personnage principal obtient des pouvoirs télépathiques après avoir jeté une pièce qui reste mystérieusement sur la tranche. Son don disparaît lorsqu'il fait tomber la pièce restée sur la tranche.
Le concept de jeu infini de pile ou face est utilisé pour illustrer l'absurde comme dans la pièce de théâtre Rosencrantz et Guildenstern sont morts de 1966, et dans son adaptation cinématographique de 1990 du même nom, de Tom Stoppard. Les deux personnages Rosencrantz et Guildenstern de la pièce de théâtre Hamlet de William Shakespeare assistent à leur propre histoire[32]. Au début de la pièce, Rosencrantz gagne 85 fois de suite au pile ou face, la très faible probabilité de cet évènement montre que la situation dans laquelle se retrouvent les personnages est absurde mais possible.
L'aspect binaire du jeu est illustré dans le dixième épisode de la cinquième saison de la série animée Futurama de Matt Groening. Le professeur Hubert Farnsworth crée un univers parallèle dans lequel le résultat du jeu de pile ou face est inversé : pile dans un univers lorsque le résultat est face dans l'autre (et vice versa).
De manière plus humoristique, dans l'épisode 15 de la dixième saison de Friends (diffusée en 2004), Joey perd 57 fois de suite contre Rachel au pile ou face avec les règles suivantes : face elle gagne, et pile il perd[33].
Modélisation mathématique[modifier | modifier le code]
Formalisme mathématique[modifier | modifier le code]
Donnons ici une formalisation mathématique de l'espace et de la loi de probabilité pour un jeu de pile ou face. C'est un cas particulier souvent utilisé en théorie des probabilités puisqu'on peut décrire explicitement les objets mathématiques.
Pour le lancer d'une pièce, l'univers des possibles est , il est composé de deux éléments 0 (ou F) pour face et 1 (ou P) pour pile. On munit cet univers fini de l'ensemble des parties . Intuitivement l'ensemble représente les résultats possibles après un lancer de pièce.
On définit alors une probabilité en donnant ses valeurs pour les événements {obtenir face} et {obtenir pile}, c'est-à-dire respectivement et : et avec . C'est-à-dire que la probabilité d'obtenir pile est p et celle d'obtenir face est 1 – p. (p = 1 – p = 1/2 pour une pièce équilibrée). Ainsi la donnée de définit mathématiquement un lancer de pièce.
Pour deux lancers successifs d'une même pièce (ou de deux pièces avec la même loi ), l'univers est dont les éléments correspondent aux résultats dans l'ordre des deux pièces. On définit une probabilité par où a et b valent 0 ou 1. C'est-à-dire que les lancers sont indépendants et que chaque lancer a la loi d'un jeu de pile ou face.
Pour deux lancers de deux pièces différentes n'ayant pas la même loi ; c'est-à-dire la première a pour loi définie avec le paramètre p et la deuxième avec la loi définie avec le paramètre q ≠ p. L'univers est encore et on définit la mesure de probabilité .
Ces définitions se généralisent pour plus de lancers.
Lois de probabilité[modifier | modifier le code]

Le lancer d'une pièce est une épreuve de Bernoulli, c'est-à-dire que l'on réalise une épreuve aléatoire dont le résultat est un succès ou un échec. Ce résultat est représenté par une variable aléatoire de la loi de Bernoulli, ses valeurs possibles sont 0 et 1 (associées à pile et face, ou inversement). Si la pièce est équilibrée, le paramètre de la loi de Bernoulli est p = 1/2, c'est-à-dire que pile et face ont la même probabilité d'apparaître. Si la pièce n'est pas équilibrée, le paramètre p de la loi de Bernoulli ne vaut pas 1/2 et un côté de la pièce a plus de chance d'apparaître que l'autre. Si p > 1/2, . Remarquons que dans la théorie des probabilités, la pièce est supposée parfaite au sens où la pièce ne peut pas tomber sur la tranche.
Donnons un lien avec la loi binomiale. Lorsque l'on effectue plusieurs lancers de la même pièce, ou de pièces ayant le même équilibrage, les lancers sont supposés indépendants. Le nombre de fois où apparaît le côté pile sur n lancers suit une loi binomiale B(n, p) où le paramètre p est la probabilité que le côté associé au résultat 1 apparaisse.
Il existe également un lien avec la loi géométrique. Si la probabilité d'obtenir pile est p et la probabilité d'obtenir face est 1 – p (p = 1 – p = 1/2 dans le cas équilibré), alors la probabilité d'obtenir face pour les n premiers lancers et pile pour le n+1e lancer est égale à (1-p)np. Le nombre de lancers nécessaires pour l'apparition du premier côté pile suit donc une loi géométrique.
Des liens avec d'autres lois de probabilité sont possibles en utilisant des résultats asymptotiques, la loi normale, par exemple, en faisant tendre n vers l'infini (voir la convergence vers la loi normale).

Faire tendre n vers l'infini revient à considérer un nombre de lancers qui tend vers l'infini. Pour une infinité de lancers d'une pièce, le fait qu'une séquence de 100 face consécutifs soit réalisée une infinité de fois, est un événement queue, c'est-à-dire que sa probabilité est 0 ou 1. C'est la loi du zéro un de Kolmogorov.
Le jeu de pile ou face permet d'aborder beaucoup de notions probabilistes, il a été inscrit dans la liste des épreuves orales du concours de l'agrégation de mathématiques.
« Le jeu de pile ou face, dont le principe est si simple, possède un très grand caractère de généralité et conduit, lorsqu’on l’étudie en détail, aux mathématiques les plus élevées. »
— Émile Borel, Principes et Formules classiques du Calcul des Probabilités, Chapitre V : Jeu de pile ou face ; 1924[34]
La modélisation mathématique du jeu de pile ou face, ou l'utilisation de la loi de Bernoulli, a été utilisée comme première approche pour des résultats mathématiques applicables à des lois plus générales :
- Dans son œuvre posthume Ars Conjectandi publié en 1713, Jacques Bernoulli énonce une première version de la loi des grands nombres pour des variables de Bernoulli . Notons la somme du nombre de pile obtenues pour n lancers. Alors la moyenne du nombre de pile converge (en probabilité) vers la probabilité p d'obtenir pile quand on réalise un grand nombre de lancers :
pour tout - Pierre-Simon de Laplace donne une première version du théorème central limite en 1812 qui ne s'applique alors que pour une variable à deux états[35]. Son résultat généralise celui d'Abraham de Moivre de 1733 démontré pour le cas particulier p=1/2. En reprenant les notations précédentes, pour tous tels que a < b :
.
Retour à l'équilibre[modifier | modifier le code]
Considérons un jeu classique de pile ou face entre deux joueurs avec une mise de 1 à chaque partie. On s'intéresse au gain d'un des deux joueurs au cours d'une partie contenant une infinité de jeu de pile ou face. On suppose que les joueurs n'ont pas de limite d'argent (fortune infinie) et que la fortune peut éventuellement être négative. D'après un théorème de George Pólya, les deux joueurs retrouveront leurs fortunes initiales une infinité de fois au cours de la partie[36]. Il est à noter que lorsqu’un joueur retrouve sa fortune initiale, l'autre également. Le nombre de parties nécessaires pour revenir à la fortune initiale est une variable aléatoire, cette variable est finie mais son espérance est infinie.
De manière plus mathématique, le gain d'un joueur au cours de la partie est une marche aléatoire dont chaque pas est +1 pour une victoire du joueur et -1 pour une défaite. Le temps de retour à la fortune initiale est le premier retour en 0 de la marche aléatoire : . Cette variable aléatoire a pour loi[36]
- .
Par un calcul simple, on en déduit que l'espérance est infinie.
Le jeu avec une vraie pièce est-il juste ?[modifier | modifier le code]
Une étude statistique a été réalisée par deux médecins sur des patients en oto-laryngologie à Vancouver[37]. Ils ont demandé à treize patients de faire trois cents lancers chacun et d'essayer d'obtenir face. Ces patients ont reçu une formation de manipulation de pièces et ont pu s'exercer quelques minutes avant l'expérience.
Les treize patients ont réussi à obtenir plus de face que de pile, dont sept patients de manière statistiquement significative. Le meilleur a obtenu 68 % de face. Il est à noter que les deux meilleurs patients ont été motivés par une récompense (pécuniaire) avant l'expérience.
Différentes explications sont données : on peut biaiser le résultat avec de l'exercice sur la manipulation de pièce (c'est le cas pour certains magiciens qui réalisent une illusion de rotation de la pièce), le résultat peut dépendre de l'orientation de la pièce avant le lancer, de la surface de réception (avec la main ou sur une surface fixe comme une table) et des propriétés intrinsèques de la pièce (la pièce belge de 1 euro tomberait plus de fois sur face[37]).
Déterminer si la pièce est faussée[modifier | modifier le code]
La question que l'on se pose est : « Étant donnée une pièce de monnaie, est-elle équilibrée ou non ? » Donnons plusieurs méthodes expérimentales pour y répondre. On suppose ici, par rapport à la sous-section précédente, que le lancer de pièce en lui-même est équiprobable.
- Utilisation de la loi des grands nombres.
- La loi des grands nombres assure que si on effectue un grand nombre de lancers, la moyenne du nombre de côtés pile obtenu est proche de 1/2. L'idée première est donc de lancer la pièce « un grand nombre de fois », de calculer la moyenne du nombre de pile et de le comparer avec 1/2. Cette méthode a cependant ses limites puisque l'on ne peut lancer une infinité de fois.
- Utilisation de l'inégalité de Bienaymé-Tchebychev.
- L'inégalité de Bienaymé-Tchebychev appliquée au nombre Yn de pile obtenus pour n lancers s'écrit de la manière suivante : , pour tout a. Par exemple, pour quarante lancers, . Cette inégalité permet d'évaluer la probabilité que le nombre de pile observé (valeur théorique) soit éloigné du nombre de pile théorique, cependant elle n'est pas suffisamment précise pour décider si la pièce est biaisée ou non.

Courbe, dite « en cloche », de la loi normale.
- L'inégalité de Bienaymé-Tchebychev appliquée au nombre Yn de pile obtenus pour n lancers s'écrit de la manière suivante : , pour tout a. Par exemple, pour quarante lancers, . Cette inégalité permet d'évaluer la probabilité que le nombre de pile observé (valeur théorique) soit éloigné du nombre de pile théorique, cependant elle n'est pas suffisamment précise pour décider si la pièce est biaisée ou non.
- Utilisation du théorème central limite.
- Le théorème central limite appliqué au nombre Yn de pile obtenus pour n lancers correspond au théorème de Moivre-Laplace, il assure que, pour une pièce équilibrée, est proche de . On utilise alors une table de loi normale[38] pour obtenir une valeur approchée de cette intégrale. Ainsi, pour 40 lancers, , en prenant b=1,58, on obtient . C'est-à-dire, avec une probabilité 0,89, le nombre de pile pour quarante lancers est entre quinze et vingt-cinq. Ce résultat, plus précis que l'inégalité précédente, n'est valide que pour « n grand », n>36 d'après le théorème de Moivre-Laplace. Une meilleure méthode est d'utiliser un test statistique.
- Réalisons le test statistique du χ² à un degré de liberté puisque l'on vérifie une unique valeur : le nombre de pile, c'est un test bilatéral. (Voir également le déroulement d'un test d'hypothèse.)
- 1re étape : On formule l'hypothèse nulle H0 et on fixe un seuil α. L'hypothèse H0 est l'évènement dont on veut connaitre la probabilité : H0=[la pièce a une chance sur deux de tomber sur pile]. Le seuil α est le pourcentage en dessous duquel on est prêt à rejeter l'hypothèse H0 (souvent α= 5 % ou 1 %).
- 2e étape : On calcule la variable de décision. C'est-à-dire que l'on réalise une expérience de n lancers de pièce, puis on compte le nombre de côtés pile obtenus. Ce nombre que l'on note op est appelé la valeur empirique. Le choix de la taille de l'échantillon n'est pas évident, il doit être suffisamment petit pour être réalisable et suffisamment grand pour donner un résultat significatif. Le nombre de lancers minimal est de dix (5 divisé par la fréquence théorique : 0,5, cf. les conditions du test).
- 3e étape : On calcule la valeur de la statistique qui correspond à la distance de op à la valeur théorique p=1/2 pour le test du χ². Le χ2 observé est
- 4e étape : On compare cette statistique avec la valeur critique χ2crit calculée en fonction de la taille de l'échantillon n et du seuil α. La table suivante est calculée à partir de la loi du χ².
| fiabilité (100 % - α) | 1 % | 5 % | 10 % | 50 % | 90 % | 95 % | 99 % | 99,9 % |
|---|---|---|---|---|---|---|---|---|
| seuil (α) | 99 % | 95 % | 90 % | 50 % | 10 % | 5 % | 1 % | 0,1 % |
| χ2crit | 0,000 2 | 0,004 | 0,02 | 0,45 | 2,71 | 3,84 | 6,63 | 10,83 |
- 5e étape : Finalement, on déduit l'acceptation ou le rejet de l'hypothèse H0.
Si χ2obs > χ2crit, on rejette l'hypothèse H0 au seuil α,
si χ2obs < χ2crit, on accepte l'hypothèse H0 au seuil α.
Exemple : on réalise n=100 lancers, et on choisit un seuil α = 5 %
- si on obtient op = 61 pile et n - op = 39 face,
est supérieur à .
On rejette alors l'hypothèse la pièce est équilibrée au seuil 5 %.
C'est-à-dire : on peut affirmer, avec fiabilité 95 %, que la pièce n'est pas équilibrée. - si on obtient op = 59 pile et n - op = 41 face,
alors est inférieur à .
On ne peut pas rejeter l'hypothèse la pièce est équilibrée, au seuil 5 %.
C'est-à-dire : on ne peut pas affirmer, avec fiabilité 95 %, que la pièce n'est pas équilibrée.
Contre-intuitions[modifier | modifier le code]
Intuitivement les réponses aux deux questions suivantes semblent être identiques. Mais leur différence est source de bien des erreurs et de paradoxes mathématiques.
La question « Quelle est la probabilité d'obtenir pile au dixième lancer sachant que l'on a obtenu face sur les neuf premiers lancers ? », se pose entre le neuvième lancer et le dixième, sachant donc que l'on connait déjà les résultats des premiers lancers.
La réponse est donc 1/2 puisque les lancers de pièces sont indépendants.
Écriture mathématique :
La question « Quelle est la probabilité d'obtenir pile au dixième lancer et d'obtenir face sur les neuf premiers lancers ? » se pose quant à elle avant le premier lancer, la probabilité concernant les dix lancers.
La réponse est donc (1/2)10≈0,001.
Écriture mathématique :
Notons que la probabilité d'obtenir face au dixième lancer et d'obtenir face sur les neuf premiers lancers (autrement dit d'obtenir face sur 10 lancers consécutifs) est également (1/2)10.
Le paradoxe engendré par la différence entre ces deux questions s'appelle l'erreur du parieur. Des problèmes basés sur le jeu de pile ou face ont souvent été énoncés pour illustrer des paradoxes plus généraux. Certains sont contre-intuitifs, d'autres n'ont toujours pas été résolus. En voici quelques exemples.
Les deux pièces de d'Alembert[modifier | modifier le code]
Citons un raisonnement fallacieux du mathématicien réputé Jean le Rond D'Alembert[39]. La question est de calculer la probabilité d'obtenir au moins une fois pile en deux lancers successifs de pièces. D'après son raisonnement, il y a trois cas possibles : « obtenir pile au premier lancer », « obtenir pile au deuxième lancer » et « ne pas obtenir pile sur les deux lancers ». Parmi ces trois issues, deux sont favorables, la probabilité est donc 2/3.
Cependant, les trois cas ne sont pas équiprobables, en effet d'Alembert considérait le cas « obtenir deux fois pile » inclus dans le cas « obtenir pile au premier lancer » puisque l'obtention de pile au premier lancer finit le jeu. En incluant ce nouvel évènement, on obtient le bon résultat : 3/4.
« L'esprit de d'Alembert, habituellement juste et fin, déraisonnait complètement sur le Calcul des probabilités »
— Joseph Bertrand, Calcul des probabilités, préface
Paradoxe des trois pièces de monnaie[modifier | modifier le code]
Le terme paradoxe est dans ce cas utilisé dans le sens contre-intuitif (premier sens du wiktionnaire soit la "proposition contraire à l’opinion commune ou à la vraisemblance"), ce n'est pas un vrai paradoxe mathématique (deuxième sens du wiktionnaire soit la "proposition qui contient ou implique une contradiction").
On lance trois pièces de monnaie. Quelle est la probabilité que toutes trois retombent du même côté, que ce soit pile ou face ?
La réponse est 1/4.
Problème de la Belle au bois dormant[modifier | modifier le code]
Le problème de la Belle au bois dormant est un paradoxe probabiliste polémique où deux interprétations contradictoires coexistent.
Le dimanche soir, alors que la Belle au bois dormant est endormie, nous lançons une pièce de monnaie pour un tirage à pile ou face.
- Si la pièce tombe sur face, le lendemain (le lundi), on la réveille et on a un entretien avec elle (voir ci-dessous pour l'entretien).
- Si c’est pile, on la réveille le lundi, on a un entretien avec elle, puis on la rendort en lui administrant un somnifère à effet amnésique pour lui faire complètement oublier la journée du lundi. Enfin on la réveille à nouveau le mardi et on a un autre entretien avec elle.
Durant l'entretien, qu'il soit uniquement le lundi, ou le lundi et le mardi, on lui pose la question : « Quelle est la probabilité que la pièce soit tombée sur pile ? » La princesse est parfaitement au courant des règles.
Deux raisonnements s'opposent. Le premier consiste à ne voir que la pièce de monnaie et la Belle répond 1/2. Le second consiste à voir l'ensemble des réveils et la Belle répond 2/3.
Paradoxe de St-Pétersbourg[modifier | modifier le code]
Ce paradoxe a été énoncé en 1713 par Nicolas Bernoulli[40]. Le paradoxe de Saint-Pétersbourg se résume à la question suivante : pourquoi alors que mathématiquement l'espérance de gain à un jeu est infinie, les joueurs refusent-ils de jouer tout leur argent ? Il s'agit donc non d'un problème purement mathématique mais d'un paradoxe du comportement des êtres humains face aux événements d'une variable aléatoire dont la valeur est probablement petite, mais dont l'espérance est infinie. Dans cette situation, ne prendre en compte que cette espérance dicte une décision qu'aucun acteur raisonnable ne prendrait : il faut jouer à tout prix.
Paradoxe de Penney[modifier | modifier le code]
Cette énigme mathématique a été énoncée en 1969 par Walter Penney[41] puis reprise en détail plus tard par Martin Gardner en 1974[42],[43].
Deux joueurs A et B s'affrontent dans une série de lancers de pièce. Chacun d'eux choisit une configuration formée d'une suite de trois piles ou faces. Par exemple, A choisit la configuration PPF = (pile, pile, face), et B la configuration FPP(= face, pile, pile). On lance ensuite une pièce plusieurs fois de suite jusqu'à ce qu'une des deux configurations apparaisse, désignant ainsi le gagnant. Avec les configurations précédentes, le jeu n'est pas équilibré. B a trois fois plus de chance de gagner que A. En effet, distinguons les différents cas :
- Si le premier lancer est face, alors quoi qu'il arrive B va finir par gagner. En effet, A ne peut plus gagner car il lui faudrait obtenir PP puis F, or au moment où PP arrive, il y a alors FPP : B a gagné.
- Si les deux premiers lancers sont pile puis face, pour la même raison, B gagne.
- Si les deux premiers lancers sont pile puis pile, alors quoi qu'il arrive A gagne.
Ainsi, sur les quatre configurations possibles des deux premiers lancers (FF, FP, PF, PP), trois mènent à la victoire de B tandis qu'une seule permet à A de gagner. Ces quatre configurations étant équiprobables, il en résulte que B a bien trois fois plus de chance de gagner que A.
Un double paradoxe apparaît alors[44] :
- En premier lieu, la configuration FPP apparaît plus probablement avant la configuration PPF. Pourtant, on montre que les temps d'arrêt des deux configurations ont la même espérance : en moyenne, il faut lancer la pièce huit fois pour obtenir l'une ou l'autre des deux configurations.
- D'autre part, les configurations ayant la même espérance de temps d'arrêt que ci-dessus sont PPF, PFF, FFP et FPP, mais il est plus probable que PPF arrive avant PFF (deux chances contre une), que PFF arrive avant FFP (trois chances contre une), que FFP arrive avant FPP (deux chances contre une) et que FPP arrive avant PPF (trois chances contre une). Ainsi, il est impossible d'établir une relation d'ordre sur l'ensemble des configurations reflétant leur probabilité de gagner, puisque la hiérarchie entre configuration n'est pas transitive. Si le jeu est modifié pour que le second joueur choisisse sa configuration après le premier, on obtient une variante probabiliste du jeu pierre-papier-ciseaux.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Dans tout cet article wikipédia, les noms des deux côtés d'une pièce seront écrits en italique : pile et face et on ne les accordera pas en nombre. Le côté "pile" est celui qui contient la valeur faciale de la pièce (par exemple 1 pour 1 €). On utilisera le terme « côté » (au lieu de face) pour désigner les différentes facettes des objets. Le nom du jeu ne sera pas écrit en italique : « pile ou face ».
- Il est à noter que des études physiques ont été réalisées pour modéliser un lancer de pièce. Il apparaît qu'une petite modification des conditions initiales (vitesse de rotation et hauteur notamment) entraine des résultats différents. voir: (en) Tomaszka Kapitaniak et collègues, Understanding Coin-Tossing, vol. 32(4), The mathematical intelligencer, (lire en ligne), p. 54-58.
- En revanche, MD5 ne conviendrait pas car il est possible de lui trouver des collisions.
- doit être suffisamment grand pour que l'on ne puisse pas retrouver sa valeur en calculant par force brute toutes les valeurs possibles de hachés.
- En fait le bit de poids faible ou n'importe quel bit de peut être utilisé : il suffit que les deux joueurs se mettent d'accord au préalable sur la position du bit à observer.
- Le terme « croix ou pile » désigne le jeu de pile ou face.
Références[modifier | modifier le code]
- (en) Eliseo Andreu-Cabrera, Mar Cepero González, Javier Rojas et Juan J. Chinchilla-Mira, Play and childhood in ancient greece, Faculty of Education. University of Alicante, C. Reinwald, (DOI 10.4100/jhse.2010.53.04, lire en ligne)
- Louis Becq de Fouquières, Les jeux des anciens : Leur description, leurs origines, leurs rapports avec la religion, l'histoire, les arts et les mœurs, Université Complutense de Madrid, Journal of Human Sport & Exercise, (lire en ligne), p. 81
- Charles Victor Daremberg et Edmond Saglio, Dictionnaire des Antiquités grecques et romaines, vol. 2, t. 1, Hachette, (lire en ligne), p. 897
- Alain Perche, Introduction à la numismatique, (lire en ligne)
- Maurice Prou, Catalogue des monnaies françaises de la Bibliothèque nationale : Les monnaies carolingiennes, C.Rollin & Feuardent, (lire en ligne), xi
- Robert Lacombe, « Histoire monétaire de Saint-Domingue et de la République d'Haïti, des origines à 1874 », Revue d'histoire des colonies, vol. 43, nos 152-153, , p. 273-337 (lire en ligne, consulté le )
- Honoré de Balzac, Le Père Goriot, Librairie Nouvelle, (lire en ligne), p. 123
- Gabriel Abot de Bazinghen, Traité des monnoies, et de la jurisdiction de la Cour des monnoies, en forme de dictionnaire, vol. 2, (lire en ligne), p. 187,493
- Mercure historique et politique de Bruxelles, Université Harvard, (lire en ligne), p. 59
- « Doubles droits, doubles revers », sur Transariart.com (consulté le )
- « Ventes sur offres : Banque centrale européenne - 2 centimes d’euro, double face nationale française », (consulté le )
- (en) « How to flip a coin », sur wikihow.com (consulté le )
- (en) « Rules of the Pokémon TCG (règles du jeu de jeu Pokémon) », sur legendarypokemon.net (consulté le )
- (en) Joseph B. Keller, The Probability of Heads, vol. 93(3), The American Mathematical Monthly, (lire en ligne), p. 191-197
- Pascal Boyer, Petit compagnon des nombres et de leurs applications, Paris, Calvage et Mounet, , 648 p. (ISBN 978-2-916352-75-6), VI. Cryptographie, chap. 7.6 (« Jouer à pile ou face par téléphone »), p. 549.
- Jean-Paul Delahaye, « Des balises qui émettent du bon hasard », Pour la Science, no 509, (lire en ligne).
- Exemple de générateur de pile ou face en ligne : https://desenligne.com/pile-face/
- « Les Règles officielles de Magic the Gathering : 711. Pile ou face », sur MagicCorporation.com (consulté le )
- (en) « 2-sided Dice » (consulté le )
- [PDF] Claude Dellacherie, « Pascal et Fermat. La naissance du calcul des probabilités », 7, 8 et 9 mai 1994 (consulté le )
- Blaise Pascal, Pensées, , 267 p. (ISBN 978-1-59547-915-0, lire en ligne), L. 418 S. 680
- Richard Wilhelm, Étienne Perrot, « Le Yiking, le livre des Transformations », sur le site de l'organisme de formation Chinois.org (consulté le )
- Serge Haroche, Jean-Michel Raimond et Michel Brune, « Le Chat de Schrödinger se prête à l'expérience », La Recherche, vol. PHYSIQUE, no 301, (lire en ligne)
- André Loranger, Dictionnaire biographique et historique de la micro-informatique, MultiMondes, , 196 p. (ISBN 978-2-89544-006-2, lire en ligne), p. 70
- Laure Friedman et Claude Lesertisseur, « 1968 - LA « MATAPOF » », (consulté le )
- (en) « Un juge destitué après avoir pris une décision à pile ou face », sur 20 minutes online, (consulté le )
- « Pourquoi Clinton et Sanders ont-ils dû être départagés à pile ou face ? », sur lemonde.fr,
- Julie Anterrieu, « Certains l’aiment chaud », sur le site de la SARL FilmDeCulte (consulté le ) : « Inventeur du "toss coin" comme gimmick propre aux mafieux, se moquant d’un de ses sous-fifres qui joue avec une pièce de monnaie. »
- Jean-Luc Lacuve, « Certains l'aiment chaud », sur le site du ciné-club de Caen, (consulté le )
- Jean-Luc Lacuve, « Non, ce pays n’est pas pour le vieil homme », sur le site du ciné-club de Caen, (consulté le )
- « Références > Film > No Country for Old Man », sur le site The Simpsons Park, de neuf fans des Simpsons (consulté le )
- (en) Rosencrantz & Guildenstern sont morts sur l'Internet Movie Database
- « 1016 - Saison 10 Épisode 16 - Celui qui faisait tout pour retenir Rachel », sur le site de l'association « Fan club français de Friends » de Franck Beulé (consulté le )
- Emmanuel Lesigne, Pile ou face : Une introduction aux théorèmes limites du calcul des probabilités, vol. 2, Paris, Éditions Ellipses, , 117 p. (ISBN 978-2-7298-0679-8, lire en ligne), « Avant-propos »
- (en) John O'Connor, Edmund Robertson, « Hugo Dyonizy Steinhaus », sur The MacTutor History of Mathematics archive, School of Mathematics and Statistics, University of St Andrews, Scotland, (consulté le )
- Ph. Biane, La fonction Zêta, École polytechnique, (lire en ligne), p. 178
- (en) M. Clark et B. Westerberg, How random is the coss of a coin?, vol. 181(12), CMAJ, (DOI DOI:10.1503/cmaj.091733, lire en ligne), « Polish statisticians claimed that the 1 € coin (from Belgium), when spun on a surface, came up heads more often than tails. », E308
- [PDF] « Tables statistiques usuelles, la loi binomiale », sur le site de l'université de Lausanne (consulté le )
- M. Delannoy, Sur une question de probabilités traitée par d'Alembert, vol. 23, Bulletin de la SMF, (lire en ligne), p. 262-265
- Bernard Bru, Marie-France Bru et Kai Lai Chung, « Borel et la martingale de Saint-Pétersbourg », Revue d'histoire des mathématiques, vol. 5, no 2, , p. 181-247 (lire en ligne).
- (en) Walter Penney, « Problem 95: Penney-Ante », Journal of Recreational Mathematics, no 2, , p. 241 (ISSN 0022-412X)
- Martin Gardner, « Mathematical games », Scientific American, no 231, n°4, , p. 120-125
- (en) [PDF] Yutaka Nishiyama, « Pattern matching probabilities and paradoxes as a new variation on Penney's coin game », Ōsaka, Japon, (consulté le )
- Jean-Paul Delahaye, « Les surprises du jeu de pile ou face », Pour la Science, no 409, , p. 146-151






















![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)






























