Orthogonalité

En géométrie classique, l'orthogonalité est une propriété liée à l'existence d'un angle droit (orthos = droit, gônia = angle).
Dans l'espace, deux droites sont orthogonales si elles sont chacune parallèles à des droites se coupant en angle droit ; deux perpendiculaires étant deux droites orthogonales et sécantes. Une droite est orthogonale à un plan si elle est orthogonale aux droites du plan. On parle de vecteurs orthogonaux pour des vecteurs directeurs de droites orthogonales et de segments orthogonaux pour des segments portés par des droites orthogonales.
Cette notion d'orthogonalité se généralise dans un premier temps à des espaces euclidiens, c'est-à-dire des espaces vectoriels de dimension finie sur lesquels on peut parler de distance et d'angle grâce à la définition d'un produit scalaire : dans les espaces euclidiens, deux vecteurs sont orthogonaux si leur produit scalaire est nul. Deux sous-ensembles d'un espace euclidien sont orthogonaux si tout vecteur de l'un est orthogonal à tout vecteur de l'autre.
L'orthogonalité peut intervenir dès qu'il existe une forme bilinéaire entre deux espaces vectoriels sur un même corps.
L'orthogonalité est opératoire dans de nombreux domaines mathématiques ou physiques. Depuis la Grèce antique, l'angle droit est à la base de la démonstration de nombreux théorèmes, notamment le théorème de Pythagore. Les grands et petits axes d'une ellipse sont orthogonaux, source de multiples propriétés. En dimension finie, c'est, par exemple, un outil de classification des surfaces quadriques. En algèbre linéaire, elle est un concept très utilisé. De même, dans le cadre du théorème spectral.
L'orthogonalité s'applique aussi si les nombres sous-jacents ne sont pas réels. L'usage des nombres complexes amène à une autre géométrie, dite hermitienne. En arithmétique, l'utilisation de l'orthogonalité sur les nombres entiers permet à Joseph-Louis Lagrange (1736 - 1813) de trouver une démonstration du théorème des deux carrés de Fermat.
Géométrie d'Euclide[modifier | modifier le code]
Définitions[modifier | modifier le code]

Une première approche intuitive associe l'orthogonalité à l'angle droit. Dans ce paragraphe E est un plan équipé d'une géométrie euclidienne. Comme l'angle droit est défini à l'aide de deux droites sécantes, et que deux droites sécantes sont toujours coplanaires, il n'est pas utile d'aller plus loin. En revanche, les résultats s'appliquent encore dans notre espace usuel de dimension trois. Le plan est formalisé soit par les cinq postulats d'Euclide[1], soit, pour être parfaitement rigoureux, par les vingt axiomes de Hilbert[2]. E possède des transformations particulières, de E dans lui-même, appelées isométries. Elles conservent les distances. Ainsi, si A et B sont deux points de E et ψ une isométrie, la distance entre ψ(A) et ψ(B) est la même que celle entre A et B. Dans un tel espace, les isométries sont les translations, les rotations et les réflexions correspondant à l'image d'un miroir.
Définition 1 — Deux droites sécantes et non confondues Δ1 et Δ2 forment un angle droit, ou encore sont orthogonales, s'il existe une rotation telle que l'image de Δ1 (resp. Δ2) soit Δ2 (resp. Δ1).
La seule rotation utilisable pour cette définition est celle d'un quart de tour. Il serait possible de définir l'angle droit à l'aide d'une réflexion. Les droites Δ1 et Δ2 sont perpendiculaires si et seulement s'il existe une réflexion d'axe Δ1 qui laisse globalement invariante Δ2.
Il est aisé de remarquer que si une droite Δ2 est perpendiculaire à une droite Δ1 et si Δ2 est parallèle à une droite Δ3, alors les droites Δ1 et Δ3 forment un angle droit. La notion d'orthogonalité ne s'applique pas seulement à des droites mais, de manière plus générale à des directions. Deux droites sont dites avoir même direction si elles sont parallèles.
Définition 2 — Deux directions δ1 et δ2 sont orthogonales, ou encore forment un angle droit, s'il existe deux droites Δ1 et Δ2 de directions δ1 (resp. δ2) telles que Δ1 et Δ2 soient perpendiculaires.
Ces deux définitions se prêtent à de nombreuses généralisations. Ainsi deux segments (resp. vecteurs) (resp. bipoints) sont dits orthogonaux si leurs directions le sont. Une droite Δ est dite perpendiculaire à un plan si toute droite du plan est orthogonale à Δ.
Propriétés[modifier | modifier le code]

Pour la géométrie du triangle, la tradition consiste à utiliser le terme de perpendiculaire et non orthogonal, dans ce contexte, les deux notions sont rigoureusement équivalentes.
La propriété fondamentale de la géométrie d'Euclide est le théorème de Pythagore. Il s'exprime ainsi :
Théorème de Pythagore — Dans un triangle rectangle, le carré de la longueur de l'hypoténuse (côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des côtés de l'angle droit.
Ce résultat semble être l'un des tout premiers théorèmes connus de l'humanité. On en trouve probablement des traces à une période datant d'avant l'écriture[3]. La première démonstration connue provient d'Euclide qui vivait autour de 300 av. J.-C. ; elle est rédigée dans un texte nommé les Éléments.
La réciproque est aussi vraie. C'est-à-dire que si, avec les notations de la figure, la somme de l'aire des carrés de côté a et b est égale à l'aire du carré de côté c, alors le triangle est rectangle. Autrement dit, si A, B et C sont trois points d'un plan, l'angle formé par les segments [A, B] et [A, C] est droit si et seulement si :
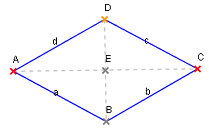
Ici, d(A, B) désigne la distance entre A et B.
Cette propriété permet de démontrer le théorème de la médiane, attribué à Apollonius de Perga[4]. Il établit que si A, B et C sont trois points du plan et si I est le milieu du segment [B, C] alors :
Le terme de médiane désigne une droite passant par un sommet et le milieu du côté opposé d'un triangle. Si un triangle A, B, C est tel que la distance entre A et B est la même que celle entre B et C, le triangle est dit isocèle. Soit I le milieu de A et C, alors le théorème de la médiane indique que :
La condition nécessaire et suffisante précédente indiquant qu'un angle est rectangle est remplie et l'angle AIB est droit. Ceci démontre que les deux diagonales d'un losange sont perpendiculaires.
Construction à la corde à treize nœuds[modifier | modifier le code]

Les propriétés de la corde à treize nœuds sont parfois utilisées par des arpenteurs pour tracer des angles droits avec un équipement minimal. Les 13 nœuds définissent 12 intervalles identiques, disposés en trois segments de longueurs 3, 4 et 5 unités (3 + 4 + 5 = 12) formant un triangle. La réciproque du théorème de Pythagore assure que, comme 32 + 42 = 52, ce triangle est rectangle.
Constructions à la règle et au compas[modifier | modifier le code]

Une première question consiste à savoir comment, à l'aide d'une règle et d'un compas, dessiner deux droites perpendiculaires. Une technique simple consiste à choisir deux points A et B sur la première droite Δ1 et à dessiner deux cercles de même rayon ayant deux points d'intersections. La droite Δ1, passant par les deux points d'intersection, est perpendiculaire à la première. La figure est un losange ; l'étude des propriétés du paragraphe précédent montre que les deux droites sont perpendiculaires.
La figure de droite montre qu'il est inutile que les deux cercles soit de même rayon. En effet, avec les notations de la figure, soit D le deuxième point d'intersection des deux cercles et O le milieu de C et D. Comme le triangle CAD est isocèle, la droite passant par A et O est perpendiculaire à celle passant par C et D. Un raisonnement analogue montre que la droite passant par B et O possède les mêmes propriétés ; elles ont donc la même direction et un point commun O, ce qui montre qu'elles sont confondues avec la droite Δ1.
Cette technique de construction d'un angle droit est ancienne. Elle date probablement de Œnopide de Chios[5], un mathématicien grec vivant cinq siècles av. J.-C.
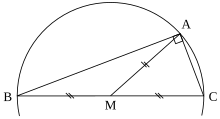
Une autre solution est illustrée par la figure de gauche. Elle consiste à tracer un cercle et un triangle dont un côté est un diamètre et dont le sommet est un point du cercle. Un tel triangle est toujours rectangle. En effet, le théorème de la médiane montre que la somme des carrés des longueurs des segments [A, B] et [A, C] est égal à quatre fois le carré du rayon, c'est-à-dire le carré de la distance entre B et C.
De nombreuses constructions à la règle et au compas utilisent les propriétés de l'orthogonalité. Elle permet de couper un angle en deux, à l'aide de la bissectrice. À l'exception du triangle équilatéral qui n'en a pas besoin, le dessin à la règle et au compas des polygones réguliers constructibles utilise les propriétés de l'orthogonalité.
Orthogonalité et théorèmes géométriques[modifier | modifier le code]

De nombreux théorèmes géométriques utilisent le théorème de Pythagore et donc l'orthogonalité pour pouvoir être démontrés. Le fait que les trois bissectrices d'un triangle soient concourantes et que leur point commun soit le centre du cercle inscrit dans le triangle provient de la propriété d'orthogonalité de la bissectrice déjà rencontrée pour construire deux droites perpendiculaires.

De même, les trois hauteurs d'un triangle d'un triangle sont concourantes. Le point d'intersection s'appelle l'orthocentre. Une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé. Un autre résultat précise que les trois médianes sont aussi concourantes. Le point d'intersection est le centre de gravité. Ce qui signifie que si un triangle est matérialisé en un solide homogène, il est en équilibre sur une pointe posée exactement sur ce point d'intersection. Leonhard Euler (1707-1783) trouve une droite remarquable. Le centre de gravité, le centre du cercle inscrit et l'orthocentre sont alignés. Cette droite passe par le centre d'un cercle étonnant appelé cercle d'Euler. Il passe par neuf points remarquables du triangle. Karl Wilhelm Feuerbach (1800 - 1834) établit son théorème affirmant que le cercle d'Euler est tangent aux trois cercles exinscrits du triangle. Tous ces théorèmes utilisent les propriétés de l'orthogonalité pour pouvoir être démontrés.
Utilisations dans d'autres contextes[modifier | modifier le code]

L'utilisation de l'orthogonalité en dehors de la géométrie date de la plus haute antiquité. Les Babyloniens utilisent un triangle rectangle isocèle de côté un pour calculer la racine de deux. L'orthogonalité d'un angle ainsi que la formule de Héron leur permettaient d'accéder à une remarquable approximation[6]. Apollonius écrit un traité sur les coniques[7] qui fascinent de nombreuses générations[8]. Il y démontre les propriétés asymptotiques des hyperboles, des foyers et la base des propriétés des polaires réciproques[7].
L'Antiquité n'est pas la seule période à utiliser des relations d'orthogonalité en géométrie. René Descartes (1596 -1650) généralise l'idée d'abscisses et d'ordonnées déjà présente chez Apollonius[9] et utilise systématiquement l'angle droit pour définir ses repères[10], ce qui permet de calculer simplement la distance entre deux points dans le plan. Elle correspond à la somme des carrés des différences des coordonnées. Il utilise son repère pour établir les lois de l'optique[11] comme celles de la réfraction et de la réflexion.
Isaac Newton (1643 - 1727) utilise des propriétés d'orthogonalité (la traduction française utilise le mot perpendiculaire) pour établir les principes du calcul différentiel. Les définitions de dérivée et d'intégrale pour cet auteur se fonde sur des raisonnements géométriques où l'orthogonalité joue un rôle majeur. Newton les utilise pour déterminer la trajectoire des planètes autour du Soleil[12]. Son formalisme correspond essentiellement à une logique analogue à celle d'Euclide ; le recours au repère cartésien est rare.
Généralisation du concept[modifier | modifier le code]
Arithmétique[modifier | modifier le code]

D'autres questions, bien éloignées de la géométrie du triangle, sont finalement résolues avec l'orthogonalité. En 1640, Pierre de Fermat se pose la question de savoir quels nombres premiers sont somme de deux carrés[13]. Les nombres 5 et 13 vérifient cette propriété, 7 et 11 non. Fermat devine juste en conjecturant que tout nombre premier impair dont le reste de la division par quatre est égal à 1 est somme de deux carrés, mais ne sait comment le démontrer. Plus d'un siècle et le talent d'Euler sont nécessaires pour en venir à bout[14]. L'équation x2 + y2 = p est enfin résolue ; elle fait partie d'une interrogation plus vaste : « Dans quel cas l'équation x2 + n y2 = p admet-elle une solution entière ? De manière plus générale, dans quel cas l'équation suivante à coefficients entiers admet-elle une solution entière ? »
Une telle expression est appelée une forme quadratique. Joseph-Louis Lagrange propose une démarche originale. Il remarque que, sous réserve de « bonnes propriétés » sur les coefficients a, b et c, la formule (1) représente le carré de la distance du point (x, y) à l'origine. La question est alors de savoir dans quel cas il existe deux vecteurs à coefficients entiers orthogonaux et de « longueur 1 ». Lagrange trouve la condition nécessaire et suffisante qui lui permet de conclure[15]. Ce raisonnement lui permet de résoudre l'équation x2 + n y2 = p si n est égal à 1, 2, 3, 4 ou 5. Le cas général reste hors de portée. Il faut encore plus d'un siècle d'efforts et le talent de nombreux géomètres, souvent allemands, pour en venir à bout[16]. L'arithmétique fait ainsi usage de l'orthogonalité, cependant, à la différence de ce que l'on trouve dans la géométrie des Grecs, les nombres associés sont limités aux entiers. La théorie voit un enrichissement à d'autres ensembles de nombres.
Dimension quelconque[modifier | modifier le code]

Une autre question impose une nouvelle généralisation. Depuis Newton, la trajectoire des planètes, essentiellement sous l'influence du Soleil, est relativement bien connue. Cependant, les planètes s'attirent entre elles, créant de petites perturbations par rapport à l'approximation de Newton, appelées variations séculaires. Lagrange cherche à démontrer que les variations du premier ordre ne peuvent déstabiliser le système[17]. Augustin Louis Cauchy (1789 - 1857) découvre que cette question est aussi associée à une forme quadratique. Il remarque qu'une équation de type (1) généralisée à la dimension trois définit une surface quadrique comme l'ellipsoïde de la figure de droite. Trouver les bons vecteurs orthogonaux pour cette quadrique lui permet de les classifier toutes[18]. Cette méthode résout aussi la question de Lagrange dans le cas où seulement trois planètes sont prises en compte[19].
La preuve de Cauchy est parcellaire : il existe plus de trois planètes. Pour résoudre le cas général, il faut pouvoir trouver autant de vecteurs orthogonaux qu'il existe de planètes. Cette question, consistant à trouver une « bonne » famille de vecteurs orthogonaux pour une forme quadratique, est finalement résolue[20] par Karl Weierstrass en 1858. Si l'avancée mathématique est certaine, la preuve de la stabilité du système solaire n'est toujours pas faite. L'astronome Urbain Le Verrier (1811 - 1877) montre que les termes d'ordre deux ne peuvent être négligés[21].
Si les conséquences en astronomie restent douteuses, une chose est néanmoins établie : l'orthogonalité ne peut plus se limiter à la dimension trois ; les services qu'elle rend sont appréciables en mathématiques comme en physique sur des espaces de dimension quelconque[22].
Forme bilinéaire[modifier | modifier le code]
La généralisation n'est néanmoins pas encore totale. Vers la fin du XIXe siècle, Ferdinand Georg Frobenius découvre une nouvelle méthode pour étudier les groupes finis. Il les représente par un groupe d'applications linéaires. Il démontre que, pour un groupe donné, chaque représentation est construite à partir d'un nombre fini de briques élémentaires[23]. Pour chacune de ces briques élémentaires, il considère une fonction, qui à chaque élément du groupe associe la trace de l'application linéaire associée. Cette application s'appelle le caractère de la représentation. Les caractères des briques élémentaires sont tous orthogonaux entre eux[24]. Cette propriété permet de déterminer simplement quelles briques élémentaires sont utilisées pour une représentation donnée. Elle est un des fondements de la théorie. Cette orthogonalité s'exprime à l'aide d'une forme bilinéaire symétrique, absolument équivalente à une forme quadratique.
Les groupes apparaissent comme un sous-ensemble de rotations dans l'espace. Si les ensembles de nombres choisis sont finis, le groupe des rotations est nécessairement fini. Cette méthode permet de construire des groupes simples, briques élémentaires pour la construction de tout groupe fini. Ces ensembles de nombres ne sont plus ordonnés, l'équivalent de la distance ne peut donc être toujours positive. Frobenius n'est de loin pas le premier à s'intéresser à cette configuration. Euler étudiait déjà en arithmétique un problème analogue à celui de Fermat : x2 – n y2 = 1 avec une forme quadratique pas toujours positive[25]. James Joseph Sylvester trouve en 1852 une loi portant son nom qui indique que toutes les bases orthogonales contiennent le même nombre de vecteurs ayant une « distance positive » et le même nombre ayant une « distance négative »[26]. Le concept d'orthogonalité s'applique alors à une forme bilinéaire, qui ne correspond plus nécessairement à une distance euclidienne. En effet, au sens propre, une distance est toujours positive.
Le formalisme moderne est plus tardif que la découverte des théorèmes fondamentaux. Les mathématiciens les découvrent souvent bien avant qu'une présentation simple et didactique soit disponible. Par exemple, le produit scalaire est une forme bilinéaire correspondant à une géométrie euclidienne. Sa définition est l'œuvre d'Hermann Weyl et date de 1918[27]. Avec ce formalisme, les termes « angle droit » et « perpendiculaire » ne sont plus utilisés.
Définitions formelles[modifier | modifier le code]
Soit (.|.) une forme bilinéaire définie sur le produit E×F de deux espaces vectoriels sur un corps commutatif K.
Définition 1 — On dit qu'un vecteur x de E et un vecteur y de F sont orthogonaux pour la forme bilinéaire (.|.), et on note x⊥y, si
D'une manière plus générale, on dit qu'une partie X de E et une partie Y de F sont orthogonales, et on note X⊥Y si, pour tout élément x de X et tout élément y de Y, le scalaire (x|y) est nul.
Définition 2 — L'orthogonal d'une partie X de E, noté X⊥, est le sous-espace vectoriel de F constitué des vecteurs orthogonaux à tous les vecteurs de X :
On définit de même l'orthogonal Y⊥ d'une partie Y de F. Pour toute partie Φ de E ou F, l'orthogonal de Φ est égal à celui du sous-espace engendré par Φ, ce qui dispense d'étudier des orthogonaux de parties Φ autres que des sous-espaces vectoriels.
Dans le cas où F est le dual de E et où la forme bilinéaire (.|.) est le crochet de dualité (aussi appelé appariement dual canonique), l'orthogonal, que l'on appelle plutôt annulateur dans ce contexte, dans E* de X ⊂ E est noté X° et de même, l'annulateur dans E de Y ⊂ E* est noté °Y.
Dimension finie[modifier | modifier le code]
Espace euclidien[modifier | modifier le code]
Un espace euclidien E est un espace vectoriel réel de dimension finie, ici notée n et muni d'un produit scalaire (.|.). Au lieu de point, on parle en général de vecteur. La distance d entre deux vecteurs x et y est donnée par la formule suivante :
Proposition 1 — Pour tout sous-espace F d'un espace euclidien E, l'orthogonal de F est un supplémentaire de F et l'orthogonal de F⊥ est F.
(Par exemple : l'orthogonal du vecteur nul est E et l'orthogonal de E est le sous-espace nul.)
Cette propriété apporte un intérêt à la notion de projecteur sur un sous-espace, parallèlement à son orthogonal (une telle application est nommée projection orthogonale). On en déduit aussi que l'orthogonal d'une droite vectorielle est un hyperplan et inversement et, plus généralement, la codimension d'un sous-espace est la dimension de son orthogonal.
Proposition 2 — Pour tous sous-espaces M et N de E,
On retrouve ainsi que tout sous-espace vectoriel F différent de E est intersection de p hyperplans, où p est la codimension de F. En effet, F est l'orthogonal d'un espace engendré par p vecteurs non nuls a1, … , ap donc, d'après la deuxième propriété ci-dessus, F est l'intersection des hyperplans a1⊥, … , ap⊥, ce qui s'écrit aussi :
Enfin, le procédé d'orthogonalisation de Gram-Schmidt montre l'existence d'une base orthonormée. Si (ei), pour i variant de 1 à n, est une telle base alors, d'après le cas d'égalité de l'inégalité de Bessel :
Espace hermitien[modifier | modifier le code]
Charles Hermite (1822 - 1901) généralise l'approche euclidienne sur les espaces complexes qui portent maintenant son nom. Les conditions nécessaires et suffisantes d'orthogonalité précédentes ne s'appliquent plus. Si x et y sont deux vecteurs d'un espace hermitien H, on dispose de la relation suivante :
En revanche, toutes les propriétés décrites dans le paragraphe Espace euclidien restent valables.
Forme bilinéaire symétrique[modifier | modifier le code]
Dans le cas d'une forme bilinéaire symétrique (.|.), l'orthogonal de l'espace entier E peut ne pas être réduit au vecteur nul.
Définition — Le noyau d'une forme bilinéaire symétrique est le sous-espace des vecteurs orthogonaux à l'espace entier E. Une forme bilinéaire ayant un noyau non réduit au vecteur nul est dite dégénérée.
Soit N ce noyau. L'orthogonal du vecteur nul est E. L'orthogonal de E est N (donc tout orthogonal d'une partie contient N). Sur le quotient E/N, la forme bilinéaire symétrique induite par (.|.) est non dégénérée et les propositions 1 et 2 du paragraphe « Espace euclidien » restent valides.
La réduction de Gauss montre l'existence de bases orthogonales pour (.|.). Cette réduction s'applique aux formes quadratiques, cependant « réduire » une forme quadratique, c'est-à-dire trouver une base orthogonale pour elle, revient à trouver une base orthogonale pour sa forme polaire. Sylvester va plus loin dans son analyse. Sa loi montre que si le corps des scalaires est ℝ, il existe un couple d'entiers (q, r) tel que, pour toute base orthogonale (ei), le réel (ei|ei) est strictement positif exactement q fois et strictement négatif exactement r fois (le noyau de la forme bilinéaire est donc de codimension q + r).
Le théorème de Weierstrass montre comment s'expriment les relations d'orthogonalités si deux formes bilinéaires symétriques dont l'une est définie positive sont en présence :
Théorème spectral en dimension finie — Soit E un espace vectoriel de dimension finie sur le corps des réels (resp. des complexes) et Φ, Ψ deux formes bilinéaires symétriques (resp. sesquilinéaires) sur E telles que Φ soit définie positive. Alors il existe une base B de E orthonormale pour Φ et orthogonale pour Ψ. Dans cette base, les coefficients de la matrice associée à Ψ sont tous réels.
Ce théorème est démontré dans l'article Endomorphisme autoadjoint. Il existe un équivalent de forme bilinéaire symétrique pour les espaces complexes, ce sont les formes sesquilinéaires. Tous les résultats de ce paragraphe s'appliquent aussi à ces formes.
Cas général[modifier | modifier le code]
Si la forme bilinéaire n'est pas symétrique, il existe encore un cas où il est possible de parler d'orthogonalité au sens précédent : celui des formes réflexives.
Définition — La forme bilinéaire est dite réflexive si :
La configuration est alors la même que celle de la forme bilinéaire symétrique : sur le quotient par le noyau, la forme est non dégénérée et les propositions 1 et 2 du paragraphe sur les espaces euclidiens s'appliquent. Pour une forme réflexive quelconque, l'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le noyau.
Dans le cas général, il devient nécessaire de parler d'orthogonalité à gauche et à droite. Soit Φ une famille de vecteurs, l'orthogonal à gauche de Φ est l'ensemble suivant :
Si la forme bilinéaire est définie sur un produit E×F de deux espaces vectoriels, alors l'ambigüité n'existe pas. L'orthogonal d'une famille d'éléments de E est un sous-espace vectoriel de F et réciproquement.
La codimension des noyaux à gauche et à droite N1 et N2 est la même car la forme se factorise par une forme bilinéaire non dégénérée sur le produit (E/N1)×(F/N2). Plus de détails sur les orthogonaux dans ce cas général sont donnés dans l'article Forme bilinéaire.
Dimension infinie[modifier | modifier le code]
Motivation[modifier | modifier le code]

En dimension finie, l'orthogonalité rend d'innombrables services. Il est tentant de généraliser sa définition aux espaces de dimensions quelconques et en particulier infini. Sous un formalisme un peu différent, c'est ainsi que Joseph Fourier (1768 1830) résout l'équation de la chaleur[28]. À deux fonctions f et g, on associe le produit scalaire :
Certain problèmes issus de la physique, comme l'équation de la chaleur ou celle de la corde vibrante, s'expriment comme un opérateur linéaire disposant de bonnes propriétés vis-à-vis de son adjoint. Si la configuration est particulièrement favorable, par exemple si l'opérateur est compact et autoadjoint, un résultat analogue à celui de la dimension finie apparaît. Il existe une base de vecteurs propres orthogonaux et de norme un. Le mot base prend ici une signification un peu différente de celle de la dimension finie. La famille est toujours libre, cependant ce n'est plus une combinaison linéaire qui représente un vecteur mais une série dont le carré de la norme de chaque vecteur est absolument convergente.
Puisqu'en dimension infinie les combinaisons linéaires deviennent des séries, un nouvel outil devient indispensable, la topologie, permettant de donner un sens à la limite, c'est-à-dire à l'équivalent des combinaisons linéaires. Dans le cas général, cette limite n'est garantie d'exister que si l'espace est complet. Pour cette raison, le cadre le plus simple pour étudier l'orthogonalité en dimension finie est celui d'un espace vectoriel muni d'un produit scalaire tel que la distance associée confère à l'espace la complétude. Plusieurs mathématiciens sont initiateurs de l'étude de la géométrie d'un espace vectoriel de cette nature, on peut citer Erhard Schmidt (1876 - 1959) ou encore Ivar Fredholm (1866 - 1927). David Hilbert (1862 - 1943) est néanmoins celui qui lui donne son nom[29]. John von Neumann (1903 - 1957) donne la définition moderne du concept[30].
Il existe certaines configurations où l'espace fonctionnel ne peut être équipé d'un produit scalaire. Une autre technique permet de bénéficier des propriétés d'orthogonalités, provenant de l'espace dual. En général n'est considéré que le dual topologique, c'est-à-dire celui ne contenant que les formes linéaires bornées. Une fois encore l'hypothèse de la complétude de l'espace vectoriel E est fort utile. Stefan Banach (1892 - 1945) propose la première formulation axiomatique moderne[31]. Son livre de 1932 sur la question[32] est encore une référence. Un espace de Banach est un espace vectoriel normé complet.
Espace de Banach[modifier | modifier le code]
Dans ce paragraphe E désigne un espace de Banach et E' son dual (topologique). Ainsi, le produit scalaire est remplacé par une forme bilinéaire continue souvent notée avec le crochet de dualité 〈.,.〉. Cette forme sur E'×E est l'unique étudiée ici. En effet, l'étude d'une forme bilinéaire continue quelconque sur le produit de E par un espace de Banach F s'y ramène, par composition avec un opérateur borné de F dans E'.
La définition de l'orthogonalité est l'application de la définition générale. Ainsi, pour la dualité entre E et E', l'orthogonal d'une partie Ψ* du dual est le sous-espace vectoriel de E composé des vecteurs orthogonaux à tous les vecteurs de Ψ*, alors que pour la dualité entre E' et le bidual E'' (qui ne sera pas considérée dans la suite), l'orthogonal de Ψ* serait un sous-espace de E''. (Lorsque E est réflexif, ces deux notions coïncident.)
Proposition 1 — Soit F un sous espace vectoriel de E, l'orthogonal de F⊥ est l'adhérence de F. Soit G* un sous-espace vectoriel de E', l'orthogonal de G*⊥ contient l'adhérence de G*, et lui est égal si E est réflexif.
La « proposition 2 pour les espaces euclidiens » prend ici une forme légèrement différente[33] :
Lorsque le sous-espace M + N est fermé, la situation est plus proche de la configuration euclidienne :
Proposition 3 — Les quatre propositions suivantes sont équivalentes :
- M + N est fermé dans E.
- M⊥ + N⊥ est fermé dans E'.
- M + N = (M⊥∩N⊥)⊥.
- M⊥+N⊥ = (M∩N)⊥.
Applications[modifier | modifier le code]


La première application historique de l'orthogonalité en dimension infinie a pour objectif de résoudre une équation aux dérivées partielles. La nature offre de nombreux exemples où l'équation se traduit par un opérateur linéaire. Tel est le cas, par exemple pour l'équation d'onde qui régit les mouvements d'une corde vibrante. Cette équation se résout simplement si la position initiale de la corde est une sinusoïde de période la longueur de la corde divisée par un entier. Ces cas particuliers possèdent deux propriétés importantes. L'espace vectoriel approxime aussi précisément que souhaité toutes les positions initiales que peut prendre la corde (elle est supposée ne pas rompre, ce qui signifie que la position initiale est représentée par une fonction continue). De plus cette famille sinsoïdale est orthogonale, l'inégalité de Bessel permet de déterminer une combinaison linéaire qui approxime aussi précisément que souhaité la position initiale ou propose une série convergente vers cette position. Les figures de droite et de gauche illustrent deux approximations de la fonction créneau. La linéarité de l'opérateur permet d'évaluer la trajectoire de la corde par combinaison linéaire ou série. Cette technique, consistant à décomposer une fonction sur une famille orthogonale est à l'origine d'une vaste branche des mathématiques, appelée analyse harmonique.
Pour cette raison, de nombreuses familles orthogonales ont été construites. Les polynômes orthogonaux, comme ceux de Legendre, d'Hermite ou de Laguerre sont de cette nature. Ils correspondent à trois produits scalaires différents.

Le théorème de Weierstrass possède son équivalent sur un Hilbert. L'opérateur doit non seulement être autoadjoint mais aussi compact. Cette configuration correspond à une équations intégrales étudiée par Hilbert et Schmidt. Comme en dimension finie, il existe une base de vecteurs propres orthogonaux. Cette équation intégrale possède une signification profonde en physique, elle représente par exemple les équations de Maxwell.
La bonne propriété topologique de compacité n'est pas toujours présente. L'équation de Schrödinger est un exemple d'opérateur autoadjoint non compact, il n'est d'ailleurs pas continu. S'il existe toujours des vecteurs propres et s'ils sont toujours orthogonaux, ils ne forment plus une base de l'espace des solutions. Une fois encore, il est nécessaire d'élargir les définitions pour que les concepts restent opérationnels. Une valeur λ est dite spectrale pour l'opérateur a si a – λId n'est pas inversible. Il se peut que a – λId soit injectif et non surjectif. Dans ce cas, il n'existe pas de vecteur propre. Une autre théorie devient nécessaire, appelée théorie spectrale.
La physique ne se contente pas des espaces de Hilbert. Un phénomène peut être suffisamment « discontinu » pour « sortir » du Hilbert ; il est parfois modélisé par un pic de Dirac, une espèce de fonction valant zéro partout sauf en un point où elle vaudrait l'infini. Elle représente par exemple une probabilité de présence nulle partout sauf en un point où la position est certaine. Pour « enrichir » l'espace fonctionnel, il devient nécessaire d'utiliser des Banach et la théorie des distributions. Le produit scalaire devient le crochet de dualité.
Si la physique est à l'origine de la généralisation de l'orthogonalité aux dimensions infinies, elle n'est de loin pas la seule cliente. La théorie des représentations s'étend aux groupes continus. Les caractères deviennent des fonctions du groupe à valeur dans les nombres complexes. À l'aide d'une mesure, comparable à l'intégrale sur les réels, un produit scalaire est défini. Les relations d'orthogonalités du cas fini se généralisent. Une fois encore, la décomposition en briques élémentaires est donnée par des relations d'orthogonalités entre les caractères. Cette approche consistant à décomposer une fonction sur une famille orthogonale est de même nature que celle utilisée pour étudier les mouvements d'une corde vibrante. Si le groupe choisi est celui des nombres complexes de module 1, les résultats obtenus sont identiques. On retrouve par un autre chemin la théorie de l'analyse harmonique. Il devient possible de la généraliser à bien d'autres groupes.
Applications en informatique et télécommunications[modifier | modifier le code]
Informatique[modifier | modifier le code]
Le jeu d'instructions d'un ordinateur est dit orthogonal lorsque (presque) toutes les instructions peuvent s'appliquer à tous les types de données. Un jeu d'instruction orthogonal simplifie la tâche du compilateur puisqu'il y a moins de cas particuliers à traiter : les opérations peuvent être appliquées telles quelles à n'importe quel type de donnée. Un exemple typique est le VAX ou le PDP-10.
Télécommunications[modifier | modifier le code]
Les techniques récentes de modulation numérique : OFDM et OFDMA, utilisées dans les réseaux de télévision numérique et les réseaux de téléphonie mobile de 4e et 5e générations sont basées sur l’orthogonalité des nombreuses sous-porteuses (de plusieurs centaines à plusieurs milliers) constituant le signal.
Par exemple, les réseaux mobiles 4G (WiMAX et LTE) utilisent des signaux orthogonaux les uns aux autres pour les sous-porteuses contiguës, évitant ainsi les interférences mutuelles entre sous-porteuses. Ce résultat est obtenu en choisissant un écart de fréquence entre les sous-porteuses égal à la fréquence des symboles sur chaque sous-porteuse (l'inverse de la durée du symbole).
Cela permet, en plaçant un nombre entier de cycles dans la durée du symbole, lorsque les signaux sont démodulés (par une transformée de Fourier), que leur contribution aux interférences soit égale à zéro[34] ; car le produit scalaire entre chacune des sous-porteuses est nul pendant la durée de transmission du symbole.
Notes et références[modifier | modifier le code]
- André Deledicq, Traduction d'Euclide, Peyrard, 1804. Les Éléments d'Euclide pour le collège et le Lycée, Les éditions du Kangourou, 1999
- (de) David Hilbert, Grundlagen der Geometrie, Leipzig, B.G. Teubner (1re éd. 1899), trad. (en) The Foundations of Geometry, 1902
- Des mégalithes d'Europe du Nord suivent un alignement associé à des triplets pythagoriciens, selon (en) A. Thom, « Megalithic Geometry in Standing Stones », New Scientist, 12 mars 1964, mentionné par (en) Martin Beech, « Megalithic triangles ».
- Cf. par exemple, dès 1858 : J. N. Haton de la Goupillière, « Mémoire sur une théorie nouvelle de la géométrie des masses », Journal de l'École Impériale de Polytechnique, n° 36, t. 21, p. 77
- Cette attribution est l'œuvre de Proclus, selon (en) Thomas Little Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, CUP, (1re éd. 1921) (ISBN 978-1-108-06306-7, lire en ligne), p. 175.
- (en) David Fowler et Eleanor Robson, « Square Root Approximations in Old Babylonian Mathematics : YBC 7289 in Context », Historia Mathematica, vol. 25, , p. 366-378 (lire en ligne)
- Apollonius de Perge, Les Coniques d’Apollonius de Perge, trad. P. Ver Eecke, 1922, rééd. Blanchard, Paris, 1963
- Michel Chasles en parle longuement dans son livre : Aperçu historique sur l'origine et le développement des méthodes en géométrie, Hayez, Bruxelles, 1837, p. 19.
- Charles Pierre Housel, « Les coniques d'Apollonius », Journal de mathématiques pures et appliquées, Paris, vol. 3, , p. 154 (lire en ligne)
- R. Descartes, La Géométrie, Hollande, , p. 1, lire sur Wikisource
- R. Descartes, La Dioptrique, Hollande, , lire sur Wikisource
- (la) I. Newton, Philosophiae Naturalis Principia Mathematica,
- P. Fermat, Correspondance, lettre à Marin Mersenne du 25 décembre 1640
- Le résultat est annoncé dans une lettre d'Euler à Christian Goldbach le 12 avril 1749.
- J.-L. Lagrange, « Recherches d'arithmétique, seconde partie », Nouveaux mémoires de l'Académie royale des sciences et belles lettres de Berlin, 1775 – Œuvres, vol. III, p. 759-795. Le théorème est démontré sous le nom de Lemme VII, p. 782-783
- On peut citer Carl Friedrich Gauss, Johann Peter Gustav Lejeune Dirichlet, Karl Weierstrass, Leopold Kronecker et David Hilbert. Cette histoire est analysée dans (en) F. Lemmermeyer, chap. VIII.3 « The Development of the Principal Genus Theorem », dans The Shaping of Arithmetic: after C. F. Gauss’s Disquisitiones Arithmeticae, Berlin, Heidelberg, Springer, (ISBN 978-3-540-20441-1, arXiv math/0207306), p. 529-561.
- J.-L. Lagrange, « Théorie des variations séculaires des éléments des planètes », Nouv. mém. de l’Acad. des sciences de Berlin, vol. 1, , p. 125
- A. L. Cauchy, « Sur les centres, les plans principaux et les axes principaux des surfaces du second degré », dans Exer. de math., vol. 3, = Œuvres (2)8, p. 8-35
- A. L. Cauchy, « Sur l’équation à l’aide de laquelle on détermine les inégalités séculaires du mouvement des planètes », dans Exer. de math., vol. 4, = Œuvres (2)9, p. 174-195
- (de) K. Weierstrass, « Über ein die homogenen Functionen zweiten Grades betreffendes Theorem », M’ber. Akad. der Wiss. Berlin, , traduction Frédéric Brechenmacher
- Jacques Laskar, « La stabilité du système solaire », dans Amy Dahan-Dalmedico, Jean-Luc Chabert et Karine Chemla, Chaos et déterminisme, Seuil, 1992 (ISBN 978-202015182-5)., chap. 7, p. 184-187 et (en) Chaos in the Solar System
- L'analyse des prolégomènes du théorème de Weierstrass provient de F. Brechenmacher, « L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes (1766-1874) », Sciences et Techniques en Perspective, 2e série, vol. 1, , p. 5-85, arXiv:0704.2931
- (de) G. Frobenius, « Über die Darstellung der endlichen Gruppen durch linear Substitutionen », S.-B. Preuss. Akad. Wiss. Berlin, , p. 994-1015
- (de) G. Frobenius, « Zur Theorie der Scharen bilinearer Formen », Zürich Naturf. Ges, vol. 41, no 2, , p. 20-23
- Cette équation porte le nom de Pell-Fermat. Son histoire est étudiée dans (en) André Weil, Number Theory : An approach through history from Hammurapi to Legendre [détail des éditions].
- (en) J. J. Sylvester, « A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of sum of positive and negative square », Philos. Mag., vol. IV, , p. 138-142 (lire en ligne)
- H. Weyl, Temps, espace, matière, A. Blanchard, (ISBN 978-2-85367-033-3)
- J. Fourier, Théorie analytique de la chaleur, Paris, Firmin Didot Père et Fils, , rééd. Jacques Gabay, 1988 (ISBN 2876470462)
- (en) Hermann Weyl, « David Hilbert and His Mathematical Work », Bull. Amer. Math. Soc., vol. 60, , p. 612-654 (lire en ligne)
- (de) J. von Neumann, « Zur Algebra der Funktionaloperatonen », Mathematische Annalen, vol. 102, , p. 370-427
- S. Banach, « Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales », Fundamenta Mathematicae, vol. 3, , p. 133-181 (lire en ligne)
- S. Banach, Théorie des opérations linéaires, Chelsea Pub. Co., , 2e éd. (ISBN 0-8284-0110-1, lire en ligne)
- Les propositions 2 et 3 et leurs démonstrations sont en partie inspirées de Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions], p. 23-26. Voir aussi (en) Tosio Kato, Perturbation Theory for Linear Operators, Springer, coll. « Grund. math. Wiss. » (no 132), , 2e éd., 623 p. (ISBN 978-3-540-58661-6, lire en ligne), p. 221. Remarquons qu'en général (même pour deux sous-espaces fermés d'un espace de Hilbert), l'inclusion de F1⊥+F2⊥ dans (F1∩F2)⊥ est stricte. La proposition 3 caractérise le cas d'égalité.
- [PDF] [http://www.supelec.fr/d2ri/flexibleradio/cours/cours-ofdm-french.pdf Cours Supélec sur OFDM /OFDMA, Mérouane Debbah supelec.fr, consulté en mars 2013.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Ouvrages[modifier | modifier le code]
- F. Casiro et A. Deledicq, Pythagore et Thalès, Les éditions du Kangourou, 1998 (ISBN 2-87694-040-X) Un ouvrage didactique sur les bases de la géométrie avec quelques éléments relatifs à l'histoire. Il couvre l'orthogonalité pour la géométrie d'Euclide
- Y. Sortais, La Géométrie du triangle. Exercices résolus, Hermann, 1997 (ISBN 270561429X) Ce livre s'adresse essentiellement aux élèves de la seconde à la terminale, ainsi qu'à leur professeur. Il propose des exercices sur le théorème de Thalès, la projection orthogonale, l'homothétie, la symétrie et la rotation, le calcul barycentrique, le produit scalaire, ou encore la notion d'angle.
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
- Bruno Ingrao, Coniques projectives, affines et métriques, Calvage & Mounet, (ISBN 978-2916352121)
- Y. Ladegaillerie, Géométrie pour le CAPES de mathématiques, Ellipses Marketing, 2002 (ISBN 2729811486) Ce livre traite de géométrie élémentaire au programme du CAPES. Il contient plus de 600 figures géométriques et couvre la géométrie affine euclidienne ainsi que l'algèbre linéaire élémentaire.
- Serge Lang, Algèbre [détail des éditions] Ce livre couvre de manière extensive l'orthogonalité en dimension finie. Il est d'un niveau soutenu pour la dimension finie.
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] Haïm Brezis propose une introduction à l'analyse fonctionnelle. Le livre présente à la fois l'aspect théorique et les applications.
- (en) B. Beauzamy, Introduction to Banach spaces and their geometry, Elsevier Science, 1985 (ISBN 0444878785) Un livre spécialisé sur les espaces de Banach. S'il est relativement exhaustif, son niveau est soutenu.
Liens externes[modifier | modifier le code]
- Orthogonalité dans l'espace par J. Onillon 2003. Ce site couvre le paragraphe intitulé géométrie d'Euclide.
- Géométrie dans l'espace en seconde par D. Nivaud 2001
- Orthogonalité les-mathematiques.net par C.Antonini et al., 2001
- Orthogonalité, orthogonalisation de Gram-Schmidt par L'Université de Nantes A. Morame 2006
- Compléments d'algèbre bilinéaire Mortajine A. Latif de l'Université Henri Poincaré-Nancy 1 2007









![{\displaystyle F=\{x\in E~|~\forall i\in [\![1,p]\!]\;(a_{i}|x)=0\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d67e05cc023e3f7295ee5554bfff6cff402e2e)












