Projection orthogonale

En mathématiques, la projection orthogonale est une transformation de l'espace, une application linéaire :

• en géométrie plane, c'est une projection telle que les deux droites — la droite sur laquelle on projette et la direction de projection — sont perpendiculaires ;
• en géométrie dans l'espace, c'est une projection telle que la droite et le plan — quels que soient leurs rôles respectifs — sont perpendiculaires.

La projection orthogonale est un type de perspective très utilisée en dessin (géométrie descriptive), et en infographie : la génération des figures est simple, par contre, on ne peut pas représenter l'éloignement (la taille des objets ne varie pas avec la distance).

De manière plus générale, en algèbre linéaire, une projection orthogonale est un projecteur tel que les deux sous-espaces sont orthogonaux.

La projection orthogonale permet de résoudre le problème de la plus courte distance d'un point à une droite, d'un point à un plan, ou plus généralement d'un point à un sous-espace affine d'un espace euclidien d'autre part. On peut alors utiliser ce concept pour résoudre des problèmes de type «moindres carrés».

L'idée générale, basée sur le théorème de Pythagore, est que le problème de plus courte distance se ramène à une propriété d'orthogonalité.

Le fil à plomb est un outil qui permet de visualiser la projection orthogonale d'un point sur un plan (en première analyse du moins).

Dessin par projection orthogonale

Exemple de projection orthogonale sur un plan

Les projections orthogonales sont utilisées pour le dessin, notamment le dessin technique et les jeux vidéo. On distingue typiquement deux types de projections utilisées :

• la géométrie descriptive : le plan de projection contient deux des axes du repère orthonormé direct ;
• la perspective axonométrique : le plan de projection est distinct des plans sus-cités.

Voir ces articles.

Projection orthogonale en géométrie affine « élémentaire »

Projeté orthogonal sur une droite, distance

L'exemple le plus simple de projection se situe dans le plan usuel (affine euclidien) : la projection orthogonale d'un point A sur une droite (D), est le point H appartenant à (D) tel que les droites (D) et (AH) soient perpendiculaires. On utilise souvent l'expression «abaisser la perpendiculaire issue de A» pour la construction de H, qui peut se faire à la règle et au compas. Mais aussi en effectuant le produit scalaire.

La distance AH est alors inférieure aux distances AM pour les autres points M de (D), strictement sauf si M=H.

Cette distance est appelée distance du point A à la droite D. Le calcul explicite peut se faire par l'application des formules de trigonométrie pour les triangles rectangles.

Le point A est sur la droite D si et seulement s'il est égal à son projeté (A=H), ou encore si et seulement si sa distance à D est nulle.

Projection orthogonale d'une droite sur une autre droite

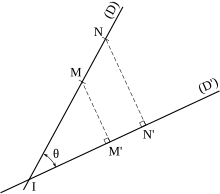
Toujours dans le plan affine euclidien, on peut considérer deux droites sécantes (D) et (D') formant un angle θ. La projection orthogonale est l'application p qui à chaque point M de (D) associe son projeté orthogonal H=p(M) sur (D').

Le point d'intersection I est son propre projeté : p(I)=I.

Une propriété remarquable de la projection est la façon dont elle transforme les distances. Si M et N sont des points de (D) et M'=p(M), N'=p(N) leur projeté orthogonal respectif, on obtient M'N'=MN.cos θ.

Notamment on remarquera, par parité de la fonction cosinus, que projeter orthogonalement les éléments de (D) sur (D') multiplie toutes les distances par un facteur cos θ, mais projeter orthogonalement les éléments de (D') sur (D) multiplie toutes les distances par le même facteur.

Projection orthogonale dans un espace vectoriel préhilbertien

Les projections orthogonales sont des endomorphismes qui font partie de la classe plus générale des projecteurs, qu'on peut alors considérer, a contrario, comme des projections «obliques».

On se place dans un espace préhilbertien E, de dimension quelconque. On se donne un sous-espace vectoriel F de E. Le problème de projection orthogonale sur F peut être énoncé ainsi : peut-on décomposer un vecteur quelconque de E en une composante sur F et une composante orthogonale à F ? La réponse dépendra en fait de l'espace F considéré.

Projection orthogonale sur une droite vectorielle

Si F est une droite vectorielle engendrée par le vecteur a, l'ensemble des vecteurs orthogonaux à F est un hyperplan appelé hyperplan normal à F et défini par

$F^\perp = \{ h\in E, (h\cdot a)=0\}~$

Si x est un vecteur arbitraire de E, on peut toujours le décomposer de la façon suivante

$x=x_F+x_\perp$ avec $x_F = \dfrac{(x\cdot a)}{\|a\|^2} a$

Et on constate que x_F est dans F, tandis que $x_\perp=x-x_F$ est dans l'hyperplan normal à F.

Il est donc toujours possible d'effectuer une projection orthogonale sur une droite vectorielle.

Transitivité

Si G⊂F⊂E et si b est le projeté orthogonal de a sur F et c le projeté orthogonal de b sur G alors c est le projeté orthogonal de a sur G. Ceci généralise le « théorème des trois perpendiculaires », qui correspond au cas où E est l'espace euclidien de dimension 3, F est un plan de E, et G une droite de ce plan.

Existence d'une projection orthogonale

On peut donner un exemple d'espace F pour lequel la notion de projection orthogonale sur F n'a pas de sens. Ainsi si on considère l'espace $\R[X]$ des polynômes réels muni de son produit scalaire usuel, et F l'hyperplan Vect(1 + X,1 + X²,...,1 + Xⁿ,...), l'ensemble des vecteurs orthogonaux à F est réduit à {0}. On ne peut donc décomposer les éléments de E, autres que ceux de F, en un élément de F et un élément orthogonal.

Cet exemple est frappant : alors qu'une droite a toujours un supplémentaire orthogonal (unique d'ailleurs), un hyperplan peut très bien n'avoir aucun supplémentaire orthogonal. Il est difficile de faire un dessin convaincant pour une telle situation !

Plus généralement on a équivalence entre les propriétés suivantes

1. il existe une projection orthogonale sur F,
2. F admet un supplémentaire orthogonal,
3. F^⊥ est le supplémentaire orthogonal de F.

Ceci montre au passage que le supplémentaire orthogonal, s'il existe, est unique.

Lorsque F admet un supplémentaire orthogonal, (F^⊥)^⊥=F donc F est nécessairement fermé, puisque l'orthogonal d'un sous-espace vectoriel l'est.

Un cas d'existence important

• On peut généraliser la formule de projection sur une droite si F est de dimension finie. En effet, en considérant une base orthonormale (e₁,...,e_n) de F, on exhibe la décomposition

$x=x_F+x_\perp$ avec $x_F = \sum_{i=1}^n (e_i\cdot x) e_i$

Attention à ne pas appliquer cette formule avec une base de F quelconque !

• Si E est un espace de Hilbert et F un sous-espace vectoriel fermé, alors l'orthogonal de F est un supplémentaire de F dans E.

• Le point commun entre les deux conditions suffisantes ci-dessus est qu'elles entraînent la complétude de F (tout sous-espace de dimension finie d'un préhilbert est complet, et tout sous-espace fermé d'un Hilbert également). Cette hypothèse plus faible est en fait suffisante :

Si F est un sous-espace complet d'un espace préhilbertien E alors l'orthogonal de F est un supplémentaire de F dans E.

Deux preuves sont présentées dans Théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert.

Minimisation de la distance

La distance d'un vecteur x au sous-espace F est par définition la borne inférieure des distances de x à tous les vecteurs de F :

$d(x,F)=\inf_{y\in F}\|x-y\|.$

Si le sous-espace F admet un supplémentaire orthogonal, le projeté orthogonal p(x) de x sur F est le point de F le plus proche de x (donc l'inf ci-dessus est en fait un min), ce qui fournit une définition alternative de p(x) :

$\big(y\in F\ {\rm et}\ d(x,F)=\|x-y\|)\Leftrightarrow y=p(x)$.

En effet, non seulement ||x-p(x)|| majore la distance d(x,F) (puisqu'il fait partie des ||x-y|| dont d(x,F) est l'inf), mais il la minore également : pour tout y de F distinct de p(x) on a même ||x-y||>||x-p(x)||, d'après l'identité de Pythagore.

Cette propriété est généralisée dans l'article théorème de projection sur un convexe.

Caractérisations parmi les projecteurs

Par la norme subordonnée

Une application linéaire p sur l'espace préhilbertien E est k-lipschitzienne sur E si et seulement si

$\forall x \in E, \|p(x)\|\leq k\|x\|~$,

et la norme subordonnée de p est alors la plus petite des constantes k telles que p soit k-lipschitzienne.

On peut alors énoncer la caractérisation :

Soit p un projecteur de l'espace préhilbertien E, les trois conditions suivantes sont équivalentes :

1. p est une projection orthogonale
2. p est 1-lipschitzienne
3. la norme subordonnée de p est égale à 0 ou 1.

Démonstration

• 1 implique 2 car si p est une projection orthogonale, les vecteurs x - p(x) et p(x) sont orthogonaux, donc le théorème de Pythagore assure que

$\|x\|^2=\|x-p(x)+p(x)\|^2=\|x-p(x)\|^2+\|p(x)\|^2 \ge \|p(x)\|^2~$.

• 2 implique 1 car si p est une projection 1-lischitzienne alors pour tous vecteurs $y \in\rm{Im}(p)~$ et $x \in\rm{Ker(p)}\setminus\{0\}~$, x et y sont orthogonaux. En effet, le projeté orthogonal z de y sur la droite vectorielle engendrée par x est nul, car z et y-z sont orthogonaux donc

$\|y\|^2=\|z\|^2+\|y-z\|^2\ge\|z\|^2+\|p(y-z)\|^2=\|z\|^2+\|y\|^2\Rightarrow\|z\|^2=0$.

• 3 implique bien sûr 2 mais réciproquement, la norme d'un projecteur 1-lispchitzien vaut 0 ou 1. En effet, la norme d'un projecteur non nul p vaut toujours au moins 1, car $\||p\||=\||p\circ p\||\le\||p\||^2$.

Par le fait d'être autoadjoint

Un projecteur de l'espace préhilbertien E est une projection orthogonale si et seulement c'est un endomorphisme autoadjoint.

Démonstration

• La condition est nécessaire car si p est une projection orthogonale alors l'égalité $(x \cdot p(y)) = (p(x) \cdot y)$ est immédiate pour des vecteurs x, y appartenant chacun à l'image ou au noyau de p, puis s'étend aux autres vecteurs, puisque ces deux espaces sont supplémentaires.
• La condition est suffisante car le noyau et l'image d'un endomorphisme autoadjoint sont orthogonaux.

Voir aussi

• Projection (géométrie)
• Projecteur (mathématiques)
• Théorème de projection sur un convexe fermé dans un espace de Hilbert
• Théorème du supplémentaire orthogonal d'un fermé dans un Hilbert
• Méthode des moindres carrés
• Pseudo-solution d'un système linéaire
• Base de Hilbert
  • Série de Fourier
  • Polynômes orthogonaux
• Déterminant de Gram