Valeur propre, vecteur propre et espace propre

En mathématiques, et plus particulièrement en algèbre linéaire, le concept de vecteur propre est une notion algébrique s'appliquant à une application linéaire d'un espace dans lui-même. Il correspond à l'étude des axes privilégiés, selon lesquels l'application se comporte comme une dilatation, multipliant les vecteurs par une même constante. Ce rapport de dilatation est appelé valeur propre, les vecteurs auxquels il s'applique s'appellent vecteurs propres, réunis en un espace propre. Le graphique de la figure 1 illustre ces notions.
La connaissance des vecteurs et valeurs propres offre une information clé sur l'application linéaire considérée. De plus, il existe de nombreux cas où cette connaissance caractérise totalement l'application linéaire.
Ce concept appartient à l'origine à une branche des mathématiques appelée algèbre linéaire. Son utilisation, cependant, dépasse maintenant de loin ce cadre. Il intervient aussi bien en mathématiques pures qu'appliquées. Il apparaît par exemple en géométrie dans l'étude des formes quadratiques, ou en analyse fonctionnelle. Il permet de résoudre des problèmes appliqués aussi variés que celui des mouvements d'une corde vibrante, le classement des pages web par Google, la détermination de la structure de l'espace-temps en théorie de la relativité générale, ou l'étude de l'équation de Schrödinger en mécanique quantique.
Histoire[modifier | modifier le code]
Genèse[modifier | modifier le code]

L'association entre la géométrie et l'algèbre, à travers la notion de coordonnées, fut introduite[1] en 1637 par René Descartes et Pierre de Fermat. Le contexte est donné pour l'apparition[2] de premiers résultats d'algèbre linéaire comme le calcul d'un déterminant. Ces résultats serviront par la suite d'outil d'analyse des valeurs propres. Cependant, les mathématiques de cette époque ne disposent pas encore des notions indispensables de l'algèbre linéaire, comme une géométrie correspondant à notre espace vectoriel, où les éléments sont définis par leurs opérations.
Le début du XIXe siècle voit l'apparition d'outils importants pour la théorie des valeurs propres. En 1799, Carl Friedrich Gauss démontre la clôture algébrique des nombres complexes[3]. Des espaces vectoriels plus vastes sont étudiés. Gauss formalise le problème de la résolution d'un système d'équations linéaires avec la méthode du pivot en retrouvant une méthode décrite par un mathématicien chinois Liu Hui (IIIe siècle apr. J.-C.) près de 1 600 ans auparavant.
Des problématiques où les valeurs propres représentent la bonne approche sont étudiées. Joseph Fourier étudie une solution[4] de l'équation de propagation à l'aide d'un outil que l'on appellera plus tard une base de vecteurs propres. Enfin en 1834, Hamilton utilise[5], un polynôme caractéristique pour trouver ce que l'on appelle maintenant les valeurs propres associées à l'endomorphisme d'une équation différentielle linéaire issue de la mécanique. Cependant, l'absence de formalisation suffisante de la notion d'espace vectoriel empêche l'apparition claire du concept.
Origine du mot[modifier | modifier le code]

La formalisation algébrique d'un espace vectoriel apparait vers le milieu du XIXe siècle. Arthur Cayley initie l'étude des espaces vectoriels de dimension n[6] et de leurs applications linéaires[7]. Grassmann formalise le concept[8]. Même si, en tant que mathématicien il est peu reconnu à cette époque, dès 1845, des idées analogues sont reprises par Cauchy et publiées sous une forme plus définitive[9] neuf ans plus tard. Sylvester utilise pour la première fois le terme de matrice[10] en 1850. Il utilise la notion de valeur propre dans le cas des formes bilinéaires pour la résolution de problèmes sur le principe mécanique de l'inertie[11] deux ans plus tard. La notion de matrice est finalement définie de manière générale et abstraite[12] par Cayley en 1858.

Jordan publie un livre[13] définitif sur les endomorphismes en dimension finie et pour une large famille de nombres, dont les complexes et réels. Jordan analyse le rôle des vecteurs propres et de leur exact domaine d'application dans une théorie maintenant connue sous le nom de réduction d'endomorphisme. La finalité de son texte n'est pas l'algèbre linéaire mais la théorie des groupes et de leurs représentations. La théorie est ainsi présentée dans le contexte des corps finis. Il termine le chapitre des valeurs propres dans le cas de la dimension finie et des corps de nombres algébriquement clos. La terminologie française provient des travaux de Jordan.
Le début du XXe siècle apporte un regard nouveau sur la géométrie. La résolution de l'équation intégrale amène certains mathématiciens à considérer une géométrie sur les ensembles de fonctions. Frigyes Riesz utilise des systèmes orthogonaux de fonctions[14]. Erhard Schmidt soutient sa thèse[15] sur un sujet analogue, sous la direction de David Hilbert. Les travaux[16] de Hilbert apportent à la notion de valeur propre une nouvelle profondeur. Ils correspondent à la formalisation de la démarche intuitive qui avait amené Fourier à la résolution de l'équation de la chaleur. Les ensembles de fonctions deviennent un espace vectoriel dont la géométrie est calquée sur celle d'Euclide. L'équation intégrale devient l'analogue d'un système linéaire et l'application linéaire prend le nom d'opérateur différentiel. Une nouvelle branche des mathématiques est née : l'analyse fonctionnelle. Elle devient rapidement le cadre général de résolution d'une large famille de problèmes mathématiques, en particulier l'analyse, les équations différentielles ou les équations aux dérivées partielles. Les valeurs propres sont un des outils essentiels à la résolution de ces problèmes. Elles s'avèrent indispensables en physique pour des théories comme la mécanique quantique ou la relativité générale. Pendant une longue période les anglo-saxons utilisent indifféremment les termes de proper value et eigenvalue, provenant respectivement de la traduction des textes de Jordan et de Hilbert. Le vocabulaire est maintenant fixé au bénéfice de la deuxième expression.
Valeur propre et XXe siècle[modifier | modifier le code]
À la fois dans le contexte de la dimension finie et pour le cas général, le XXe siècle voit un développement massif de ces théories. Le cas de dimension finie subit deux évolutions : cette théorie est généralisée à d'autres ensembles de nombres que les réels ou les complexes. De plus, des mathématiciens comme Issai Schur, Alexeï Krylov, Walter Edwin Arnoldi (en) ou Nelson Dunford développent quantités d'algorithmes pour permettre la détermination des valeurs propres. Le cas général est cependant le plus étudié. Il ouvre la voie à une branche importante tout au long de ce siècle, l'analyse fonctionnelle. La théorie des valeurs propres est alors généralisée à la théorie spectrale. Paul Dirac et John von Neumann étudient ce concept dans un cadre servant de modélisation à la physique. Israel Gelfand, Mark Naimark et Irving Segal appliquent ces concepts à des univers plus vastes, les C*-algèbres. Sur la base de résultats de géométrie algébrique trouvés par Alexandre Grothendieck, Alain Connes développe un cas particulier de C*-algèbres, les géométries non commutatives. La théorie spectrale reste encore un large champ d'investigations mathématiques, et nombre de problèmes sont toujours ouverts dans ce domaine.
Les valeurs propres et, dans son cas le plus général, la théorie spectrale ouvrent de nombreux champs d'applications à la fois théoriques et appliqués. En mathématique, cette approche permet par exemple la résolution d'équations différentielles, ou d'équations aux dérivées partielles. La physique utilise très largement la théorie spectrale : elle sert de cadre général à la mécanique quantique et permet par exemple l'étude de l'équation de Schrödinger. Les solutions de l'équation de Schrödinger indépendante du temps sont des vecteurs propres. Les théories physiques de la fin du XXe siècle comme les supercordes utilisent largement les notions de spectre dans des cadres mathématiques avancés, par exemple les géométries non commutatives. Les sciences de l'ingénieur ne sont pas en reste, même si elles se cantonnent en général à une approche de dimension finie. Elles utilisent quantité d'algorithmes issus des calculs de valeurs propres et vecteurs propres. Cette approche permet de résoudre de multiples problèmes tirés par exemple de la mécanique statique ou dynamique, des systèmes électriques et même dans d'autres secteurs comme l'économie.
Définition[modifier | modifier le code]
Définition intuitive[modifier | modifier le code]
Une application linéaire est une application qui transforme les vecteurs en conservant les propriétés d'addition des vecteurs et les rapports de colinéarité entre vecteurs. Ainsi, si un vecteur w est la somme de deux vecteurs u et v, alors l'image de w par l'application est la somme de l'image de u et de l'image de v. De plus, l'image de av est a fois l'image de v (pour tout scalaire a). Plusieurs transformations géométriques usuelles (homothétie de centre 0, rotation de centre 0) sont des applications linéaires.
La figure 2 illustre par un exemple une application linéaire. On remarque que le vecteur vert est la somme des deux vecteurs bleu et noir avant transformation, et que c'est encore le cas après. De même le vecteur bleu est le triple du vecteur rouge avant la transformation, et ça reste le cas une fois qu'on l'a appliquée. On voit un vecteur propre en noir de valeur propre 1/2 : on passe du vecteur initial au vecteur image par multiplication de rapport 1/2.
- Un vecteur est dit vecteur propre par une application linéaire s'il est non nul et si l'application ne fait que modifier sa taille sans changer sa direction (à ne pas confondre avec son sens !).
- Une valeur propre associée à un vecteur propre est le facteur de modification de taille, c’est-à-dire le nombre par lequel il faut multiplier le vecteur pour obtenir son image. Ce facteur peut être positif, négatif (renversement du sens du vecteur) ou nul (vecteur transformé en un vecteur de longueur nulle).
- Un espace propre associé à une valeur propre est l'ensemble des vecteurs propres qui ont une même valeur propre et le vecteur nul. Ils subissent tous la multiplication par le même facteur.

Définition mathématique[modifier | modifier le code]
Soit E un espace vectoriel sur K et u un endomorphisme de E, alors :
- le vecteur x de E non nul est dit vecteur propre de u si et seulement s'il existe un élément λ de K tel que u(x) = λx ;
- le scalaire λ élément de K est dit valeur propre de u si et seulement s'il existe un vecteur x non nul de E tel que u(x) = λx ;
- soit λ une valeur propre de u. Alors l'ensemble constitué des vecteurs propres de valeur propre λ et du vecteur nul forme un sous-espace vectoriel de E appelé espace propre de u associé à la valeur propre λ.
Le vocabulaire des éléments propres dans différentes disciplines[modifier | modifier le code]
- En mécanique, on étudie les fréquences propres et les modes propres des systèmes oscillants.
- En analyse fonctionnelle, une fonction propre est un vecteur propre pour un opérateur linéaire, c'est-à-dire une application linéaire agissant sur un espace de fonctions.
- En géométrie ou en optique, on parle de directions propres pour rendre compte de la courbure des surfaces.
- En théorie des graphes, une valeur propre est simplement une valeur propre de la matrice d'adjacence du graphe.
Exemples[modifier | modifier le code]
L'image dans un miroir plan est un exemple d'application linéaire. On peut remarquer que tout vecteur collé au miroir donne comme image lui-même. On en déduit que le plan du miroir est un espace propre associé à la valeur propre 1. En revanche, un vecteur perpendiculaire au miroir donne comme image un vecteur de même longueur, de même direction, mais de sens opposé. On en déduit que ce vecteur est un vecteur propre de valeur propre –1. Enfin un vecteur ni collé ni perpendiculaire donne une image qui n'est pas dans le même axe que lui, ce n'est donc pas un vecteur propre. Dans cet exemple, le comportement des vecteurs propres décrit intégralement l'application, en effet tout vecteur est la somme d'un vecteur dans le plan de la glace et d'un vecteur perpendiculaire. Et la connaissance du comportement dans le plan et dans l'axe perpendiculaire permet la détermination de la transformation de tous les vecteurs, par linéarité.
Il existe une transformation particulière, qui est centrale dans la théorie des valeurs propres. Imaginons comme application linéaire une dilatation qui éloigne par exemple tous les points d'un ballon de baudruche de son centre d'un rapport constant. Cette dilatation grandit tous les vecteurs d'un même rapport sans changer leur direction. Tous les vecteurs à l'exception du vecteur nul sont donc des vecteurs propres et il existe une unique valeur propre. On appelle cette application une homothétie.
La Terre tourne autour d'elle-même, et donc tout vecteur qui se situe sur la droite passant par les pôles reste immobile, si l'on ne considère pas le mouvement autour du Soleil. Les vecteurs de cette droite sont donc des vecteurs propres de valeur propre 1. Tout autre vecteur tournera avec la Terre et donc n'est pas propre. Si on limite l'analyse au plan de l'équateur, alors tous les vecteurs tournent et il n'y a plus de vecteurs propres. Nous retrouverons ce cas particulier dans l'étude des valeurs propres sur les nombres réels.

Les deux premiers exemples traitent d'un cas de dimension 3, comme le monde géométrique qui nous entoure. On peut cependant considérer des espaces vectoriels de dimension beaucoup plus vaste. Un exemple d'application est celui de la corde vibrante, par exemple celle d'une guitare. Chaque point de la corde oscille autour de sa position au repos. Pour chaque point de la corde, son mouvement peut être considéré comme une dimension d'un espace vectoriel ; l'espace vectoriel ainsi obtenu regroupe les mouvements de tous les points de la corde, il est de dimension infinie. À partir d'une position initiale obtenue par le doigt du guitariste, le mouvement de la corde suit une équation qu'on appelle une équation aux dérivées partielles et qui est linéaire. Les vecteurs propres sont dans ce cas des vibrations qui laissent quelques points fixes, on les appelle des ondes stationnaires. La figure 3 illustre un exemple de vibration. Le premier vecteur propre correspond à l'onde avec deux points fixes, les extrémités, le deuxième vecteur propre correspond à l'onde ayant comme point fixe supplémentaire le milieu, le troisième a deux points fixes situés au tiers et aux deux tiers en plus des extrémités, etc. Il se trouve que dans ce cas précis, les vecteurs propres décrivent totalement le comportement de la corde. De plus, si l'on tient compte dans l'équation du phénomène d'amortissement alors on remarque que l'essentiel des vecteurs propres se dissipe très vite, seul le premier vecteur propre reste longtemps, il correspond à la note qui sera émise par la corde de la guitare qui dépend donc de la longueur de la corde mais peu de l'impulsion initiale.
Applications en dimension finie[modifier | modifier le code]
Équation linéaire et valeur propre[modifier | modifier le code]
Beaucoup de problèmes finissent par se présenter sous la forme de la résolution d'un système d'équations linéaires. C’est-à-dire dans un cas simple à un système de la forme :
et dans le cas général :
On peut citer comme exemple la mécanique statique avec l'étude du cas d'un pavé sur une surface en pente.

On trouvera alors trois équations linéaires décrivant les forces de haut en bas, de droite à gauche et d'avant en arrière. Si en revanche, on considère l'équilibre statique d'une plate-forme pétrolière, plusieurs centaines d'équations linéaires sont nécessaires au calcul.
S'il est théoriquement possible de résoudre ces systèmes d'équations avec des calculs de déterminants et de comatrices, il n'est pas envisageable d'utiliser pratiquement cette méthode. Elle débouche rapidement sur une complexité et une longueur de calcul qui n'est de loin pas traitable par les ordinateurs les plus puissants d'aujourd'hui. Ceci est particulièrement vrai dans le cas d'une plateforme pétrolière par exemple.
Les mathématiciens analysent le problème sous un autre angle, le système d'équations est considéré comme la recherche d'un vecteur x dont l'image par l'application linéaire u est égale à b.
u, x et b sont décrits par une matrice et deux jeux de coordonnées :
Il suffit alors de comprendre l'application u pour résoudre plus simplement la question posée. Cette application est une application linéaire d'un ensemble dans lui-même. On appelle endomorphisme une telle application. L'espace vectoriel est décomposé en sous-espaces stables par u, c’est-à-dire que leurs images par u sont incluses dans eux-mêmes. Ils disposent de propriétés bien particulières. À eux tous ils génèrent l'espace vectoriel tout entier, mais l'endomorphisme restreint à ces sous-espaces est particulièrement simple. Un bon exemple est donné par le cas du miroir. Sur la surface du miroir l'application est simple : elle ne modifie rien ; sur la droite perpendiculaire un vecteur a pour image le vecteur opposé, et tout vecteur est bien la somme d'une composante sur le miroir et d'une composante perpendiculaire.
Illustration par un exemple numérique
Soit une équation linéaire dont la matrice A est donnée ci-dessous. La résolution par inversion impose des calculs longs et complexes. Une approche fondée par les valeurs et les vecteurs propres, la réduction de Jordan, montre que cette matrice est semblable à la matrice J :
Le problème, portant initialement sur la matrice est alors ramené à la matrice , et est donc largement simplifié. Dans cet exemple, les valeurs propres de et de sont les coefficients diagonaux de : ; à chacune de ces valeurs propres est associé un sous-espace propre, il est ici de dimension 1 pour chacune : la raison, pour 1 et 2, est que ces coefficients n'apparaissent qu'une fois sur la diagonale de ; pour 4, bien qu'il apparaisse deux fois, la dimension du sous-espace propre associé ne peut être 2, à cause de la présence du coefficient 1 au-dessus de la diagonale.
Il est toutefois à noter que cette problématique, même si elle est la première à être apparue en algèbre linéaire, n'a pas ouvert la voie à la notion développée dans cet article.
Méthode générale de résolution en dynamique[modifier | modifier le code]
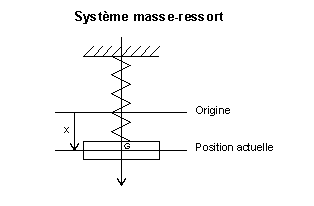
Si la problématique précédente n'a pas suffi, c'est essentiellement à cause d'une absence de concept de base. La géométrie d'alors est formalisée par le concept de point. Les points ne s'additionnent pas, ils ne possèdent pas de propriétés algébriques. La notion d'espace vectoriel actuelle n'existait pas. Hamilton, le mathématicien anglais, s'est penché sur un problème où l'addition et la multiplication scalaire sont naturelles. Ce problème lui a été fourni par la physique : les systèmes oscillants.
Le cas de la figure 4 illustre cette situation. La masse est attachée à un ressort et subit un amortissement visqueux (ce qui signifie que la dissipation due aux frottements est proportionnelle à la vitesse). Il n'existe aucune force extérieure, et le système oscillant vérifie l'équation différentielle linéaire suivante avec les notations de l'article Systèmes oscillants à un degré de liberté :
Cette équation utilise les dérivées secondes, c'est la raison pour laquelle on appelle ce type d'équation une équation différentielle linéaire d'ordre deux. Cependant, il est possible de ramener une équation d'ordre deux à une équation d'ordre un à condition de doubler la dimension de l'espace (cf. Équation différentielle linéaire). Ici, l'espace vectoriel devient de dimension 2 avec un premier axe correspondant à la vitesse, noté v, et un deuxième à la position, noté x. Si l'analyse du mouvement commence par convention à l'instant t0 = 0, l'équation (1) s'écrit alors sous la forme :

La solution d'une telle équation est connue, et s'écrit de la manière suivante :
La preuve du fait que l'exponentielle est bien la solution est donnée dans l'article Matrice diagonalisable. Il apparaît nécessaire de calculer une exponentielle d'endomorphisme, qui dépend de toutes les puissances de cet endomorphisme. Ce problème est résolu par Hamilton grâce à la notion de valeurs et vecteurs propres : en effet, s'il existe une base de vecteurs propres pour l'endomorphisme , avec pour valeurs propres λ1 et λ2 et si A est l'écriture matricielle de a, c'est-à-dire s'il existe une matrice de passage P (P représentant une base de vecteurs propres) telle que :
alors :
La solution, tant pour la position que pour la vitesse, est donc une combinaison linéaire d'exponentielles. Le calcul général de l'exponentielle d'un endomorphisme ainsi que les justifications théoriques sont traités dans l'article Réduction d'endomorphisme.
S'il existe deux valeurs propres réelles, alors la solution est de même nature que la courbe bleue sur la figure 5. L'amortissement ramène sans oscillation la masse à sa position d'équilibre. En revanche, s'il n'existe pas de valeur propre réelle, il est nécessaire d'en trouver dans les nombres complexes. La solution est alors donnée par la partie réelle de la matrice, et on obtient une trajectoire de même nature que la courbe rouge, avec des oscillations avant d'atteindre le point d'équilibre. La physique est source de nombreux exemples de problèmes linéaires de dimension finie où les valeurs propres représentent la bonne approche pour la résolution. On les trouve par exemple dans l'analyse des circuits électriques.
Principe d'inertie de Sylvester[modifier | modifier le code]
Formulation du principe d'inertie de Sylvester

Sylvester analyse l'énergie que l'on doit transmettre à un solide pour lui donner une vitesse de rotation vr. Il remarque que le vecteur propre représente dans ce contexte un axe de rotation privilégié. La valeur propre correspond à la grandeur appelée en physique moment d'inertie, elle est inversement proportionnelle à l'énergie à fournir pour atteindre une vitesse de rotation vr. Pour atteindre cette vitesse avec le moins d'énergie, il est nécessaire de choisir l'axe ayant le plus faible moment d'inertie, c’est-à-dire celui où l'ellipsoïde de la figure 14 est le plus aplati. La théorie montre que l'axe où l'inertie est la plus forte est toujours perpendiculaire à celui du plus faible moment d'inertie. Cette perpendicularité correspond à l'existence d'une base orthonormale de vecteurs propres.
Le cas du balai de la figure 6, illustre par un exemple le phénomène. L'axe de plus faible moment d'inertie est indiqué par la flèche 1. Il est intuitif que l'énergie nécessaire pour obtenir la même vitesse de rotation selon l'axe de la flèche 2 sera largement supérieure. Les vecteurs propres et les valeurs propres apparaissent comme des caractéristiques propres de la géométrie de l'objet, dans ce cas les axes privilégiés de rotations, (il est possible de prendre un axe de rotation au hasard, mais les autres axes imposeront des tensions sur l'axe) et les valeurs propres les moments d'inertie associés.
Une approche similaire s'applique en mécanique des milieux continus pour l'analyse des déformations élastiques comme la torsion, on parle alors de tenseur des contraintes.
Application en statistique
L'approche de Sylvester est utilisée dans de nombreux domaines pour comprendre la géométrie d'un phénomène. Les techniques statistiques de dépouillements de sondage en sont un parfait exemple. Soit un sondage, réalisé sur un échantillon de cent personnes et contenant six critères. S'il est possible d'évaluer chaque question par un critère numérique, alors une analyse en composante principale est possible. Elle permet d'interpréter les résultats du sondage.
Les résultats du sondage, sont dans un premier temps normalisés pour qu'un critère, qui par exemple prend des valeurs entre un et cent ne soit pas dix fois plus important qu'un autre prenant des valeurs de un à dix. Le résultat du sondage est alors considéré comme un solide dans un espace comportant autant de dimensions que de critères.
 |
 |
 |
La première figure représente l'ACP sur les deux premiers vecteurs propres, qu'on appelle en statistiques composantes principales. Les valeurs sont rassemblées autour de cet axe, ce qui signifie qu'il est le plus explicatif. Ce caractère explicatif est donné par le carré de la valeur propre. Dans l'exemple fictif, il est dû à deux critères fortement corrélés. Ce phénomène est visible sur la deuxième figure, les deux critères corrélés sont représentés. Là encore ces critères se rassemblent autour d'une droite, dans l'exemple cette droite est la droite de la composante principale (celle à la valeur propre la plus forte). Ces coordonnées sur ses deux critères sont respectivement 0,506 et -0,491. Si les critères sont revenu et surcharge pondérale, alors le sondage indique que l'obésité frappe en priorité les revenus les plus faibles. La troisième figure illustre un cas, ou la corrélation entre deux critères est faible. Si les critères sont taille et niveau d'étude, alors un tel graphique indique que la taille n'est pas un critère différenciant pour le niveau d'étude.
Cet exemple illustre encore que dans le cas analysé par Sylvester, les valeurs et vecteurs propres ne sont pas uniquement des méthodes de calculs, mais aussi des éléments constitutifs de la géométrie du problème considéré.
Application en relativité
À travers les moments d'inertie d'un solide, Sylvester ne s'est pas trompé sur le titre de son article de 1852 Théorie des invariants algébriques[réf. nécessaire]. Les valeurs propres, qui sont les invariants, dépassent de loin le cadre des moments d'inertie. La géométrie de l'espace-temps relativiste est un autre exemple. Ici la forme bilinéaire ne décrit plus le moment d'inertie d'un solide indéformable, mais une modélisation de la géométrie même de notre univers.
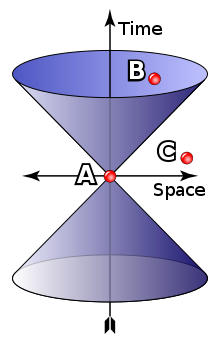
La figure 8 représentative de cette géométrie est néanmoins fort différente des illustrations précédentes. Il existe un axe particulier, où le carré de la distance possède une propriété spéciale : il est négatif. La bonne « distance » de cette théorie n'est plus toujours positive. Un vecteur de coordonnées (x, y, z, t) a pour image x2 + y2 + z2 – c2t2. Hermann Minkowski développe une approche mathématique fondée sur ces principes en 1907 dans un article intitulé Espace-temps, et l'applique à la relativité l'année suivante.
Le cône d'inertie de la figure 8 représente l'univers pour un observateur au point A. Le point C possède une distance négative, pour l'atteindre il faudrait une vitesse supérieure à celle de la lumière, ce qui, dans le contexte de cette théorie n'est pas réalisable. Il est donc inobservable et n'a aucune influence directe ou indirecte sur l'observateur. Le point B est dans ce que l'on appelle le cône de lumière, c'est un point possible, il pourra interagir avec l'observateur.
Dans le cas qui intéresse Minkowski, les endomorphismes qui traduisent les lois physiques d'un observateur à un autre observateur, jouent un rôle important ; ce sont ceux qui vérifient l'équation , où est la forme bilinéaire qui décrit la géométrie considérée. Ces endomorphismes laissent la géométrie invariante, ils correspondent dans une modélisation euclidienne aux isométries. Dans la géométrie de la relativité, 1 est valeur propre et son espace propre associé est de dimension 3 et ic est valeur propre de sous-espace propre associé de dimension 1, où i désigne le nombre imaginaire et c la vitesse de la lumière. On parle de signature de Sylvester (3, 1). Toutes les lois physiques doivent être invariantes par ces endomorphismes. Ces endomorphismes forment une structure de groupe, appelé groupe spécial unitaire, la relativité revient à réécrire la physique en lois laissées invariantes par le groupe spécial unitaire de dimension 4 et de signature (3, 1).
Représentation des groupes[modifier | modifier le code]

L'analyse par vecteurs et valeurs propres possède aussi comme domaine d'application la représentation des groupes. Une structure de groupe est parmi celles dont la définition algébrique est la plus simple, c'est un ensemble muni d'une seule opération notée souvent comme la multiplication. Si la définition est simple, en revanche, ces structures s'avèrent parfois suffisamment complexes pour que leur théorie ne soit pas encore complètement connue. Comme exemple de groupe, il est possible de citer celui des rotations du cube qui laissent son enveloppe invariante. La figure 9 montre que ce groupe est engendré par trois permutations, celle qui place la face 1 en position 2, représentée par la flèche rouge, celle représentée par la verte et enfin la bleue. Au total ce groupe comporte 24 éléments. Une représentation d'un groupe consiste à une identification de ses éléments avec des endomorphismes de telle manière que l'opération du groupe corresponde à la composition d'endomorphisme. Ainsi dans l'exemple de la figure, il existe une identification naturelle entre le groupe abstrait des 24 rotations du cube avec un groupe de rotations dans un espace de dimension 3.
Cette approche permet alors de disposer des outils comme les vecteurs ou valeurs propres pour l'analyse de la structure des groupes. La théorie montre que les espaces propres d'une représentation correspondent à la partie commutative du groupe. Dans le cas d'un groupe entièrement commutatif, il existe une base de vecteurs propres pour toute la représentation. Cette approche démontre, par exemple que les groupes commutatifs finis sont des produits de groupes cycliques. La démonstration est esquissée dans l'article Matrice diagonalisable.
La représentation des groupes finis joue un rôle important dans la théorie des vecteurs propres. Elle a permis à Jordan, dans un contexte relativement général, de comprendre totalement le champ d'application et les limites d'une approche par vecteurs propres. Des conditions nécessaires et suffisantes d'existence de vecteurs propres ou de bases de vecteurs propres sont alors connues. De plus, les cas où il n'existe pas de base de vecteurs propres sont élucidés ainsi que la structure exacte des endomorphismes entrant dans cette catégorie et la proportion d'endomorphismes de cette nature dans l'ensemble de tous les endomorphismes.
Si le contexte est relativement général, il ne couvre pas tous les cas d'espaces vectoriels connus. La théorie de Jordan se limite à la dimension finie avec un corps de nombre algébriquement clos. Un corps est dit algébriquement clos si tous ses polynômes ont au moins une racine. Ce contexte est néanmoins suffisamment général pour couvrir toutes les applications citées dans ce chapitre.
Théorie en dimension finie[modifier | modifier le code]
Approche élémentaire[modifier | modifier le code]
Une première remarque simplifie l'étude. Si λ est une valeur propre d'un endomorphisme u, alors un vecteur propre est un vecteur non nul qui a pour image 0 par l'application u – λ Id, où Id désigne l'application identité. L'espace propre associé à λ est l'ensemble des vecteurs qui ont pour image 0 par cette application. On appelle cet ensemble le noyau de l'endomorphisme u – λ Id. Les propriétés générales établissent que cet ensemble est un sous espace vectoriel. Celui-ci est non réduit à 0 par définition d'une valeur propre.
Une fonction importante, en particulier dans notre cadre, est la fonction déterminant. Elle fut la première à être étudiée systématiquement dans le monde de l'algèbre linéaire. Elle associe à un endomorphisme un nombre. Son intérêt réside notamment dans le fait que le déterminant d'un endomorphisme est nul si et seulement s'il existe des vecteurs non nuls qui ont pour image le vecteur nul par cet endomorphisme, c'est-à-dire si et seulement si 0 est une valeur propre pour cet endomorphisme. Le déterminant de l'application u – λ Id est appelé le polynôme caractéristique. Les remarques précédentes permettent d'énoncer les premières propriétés :
- Soit λ une valeur propre, alors l'espace propre de valeur propre λ est le sous-espace vectoriel égal au noyau de u – λ Id,
- un espace propre est un sous-espace vectoriel,
- les racines du polynôme caractéristique sont les valeurs propres.
Cette dernière propriété montre que l'existence de racines de polynômes a une influence sur la théorie des valeurs propres. En fait, l'existence même des valeurs propres dépend de l'existence de racines pour les polynômes, par exemple le polynôme caractéristique. C'est pourquoi dans le cadre du corps des nombres complexes, qui est algébriquement clos d'après le théorème de d'Alembert-Gauss, les propriétés liées aux valeurs propres s'énonceront plus simplement que dans le cadre du corps des réels.
Cas où l'endomorphisme est diagonalisable[modifier | modifier le code]
Article théorique : Diagonalisation ; article appliqué : Matrice diagonalisable.

Le concept de l'article est particulièrement clair dans le cas où le comportement de l'endomorphisme est entièrement décrit par les vecteurs et valeurs propres. L'endomorphisme est alors dit diagonalisable.
Un endomorphisme est dit diagonalisable s'il existe une base de vecteurs propres.
C'est le cas du premier exemple, celui du miroir. Une base peut alors être choisie en prenant deux vecteurs libres dans le plan de la glace et un troisième perpendiculaire à ce plan. Les deux premiers vecteurs ont pour images eux-mêmes et sont donc de valeur propre 1 et le dernier est de valeur propre –1. Cette situation est intéressante à trois titres :
- elle correspond à un cas simple à traiter ;
- elle est, sous certaines hypothèses, « fréquente » ;
- il existe de multiples critères pour la repérer.
- La simplicité de cette situation provient de deux faits. Il existe une décomposition de l'espace en sous-espaces stables, simples en eux-mêmes, et sur lesquels l'endomorphisme est simple à décrire. Ces sous-espaces sont simples car de dimension 1 : ce sont des droites. La linéarité de l'endomorphisme permet de connaître exhaustivement le comportement de la transformation, une fois compris le comportement sur ces droites. Enfin la restriction de l'endomorphisme à ces droites est une homothétie, c’est-à-dire une dilatation, d'un facteur la valeur propre. Un exemple de cette situation est donné par la figure 10 : un parallélotope jaune dont les arêtes sont la base de vecteurs propres, l'image par l'endomorphisme est un parallélotope dont les arêtes ont gardé les mêmes directions, mais dont les longueurs ont été modifiées.
Cette simplicité ouvre la voie à de nombreuses applications évoquées précédemment dans l'article. Elle permet par exemple le calcul d'une exponentielle d'endomorphisme et par conséquent la résolution de nombreux problèmes mécaniques.
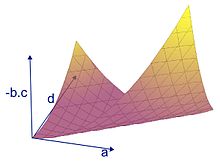
- Cette situation est aussi « fréquente ». La figure 11 en est une illustration dans le cas où l'espace est un plan vectoriel réel. L'espace vectoriel de ses endomorphismes est alors de dimension 4 : tout endomorphisme admet une représentation matricielle de la forme . Pour obtenir une représentation graphique en dimension 3, les coefficients b et c de la représentation matricielle sont représentés uniquement par un axe à travers la valeur bc. En utilisant les critères de diagonalisabilité, on constate qu'une nappe particulière, de dimension 2, apparaît dans cette représentation (elle serait de dimension 3, si l'on pouvait tout représenter dans l'espace, de dimension 4, des endomorphismes). Cette nappe correspond à une situation limite pour la diagonalisabilité : la zone en dessous de la nappe contient des endomorphismes diagonalisables, la zone au-dessus contient des endomorphismes diagonalisables sur C mais pas sur R. Dans la représentation choisie, les endomorphismes diagonalisables sur C occupent donc presque tout l'espace ; c'est en cela que le cas de diagonalisabilité est fréquent. En revanche les endomorphismes qui sont diagonalisables même sur les réels en occupent essentiellement la moitié. Cette situation de fréquence est à mettre en relation avec la situation des polynômes à coefficients réels, dont les racines sont réelles, ou seulement complexes. On trouve en particulier, dans la zone des endomorphismes diagonalisables sur C mais pas sur R, les rotations, dont un exemple avait été donné par la rotation de la Terre sur elle-même. Enfin, pour ce qui est de la nappe elle-même, deux types de situations s'y présentent. La droite horizontale d'équation a = d avec b = c = 0 représente la droite des homothéties, du même type que le deuxième exemple de l'article. Les autres points de la nappe représentent les seuls endomorphismes non diagonalisables.[réf. nécessaire]
- Enfin, il existe de multiples critères pour caractériser les endomorphismes diagonalisables. Une première approche consiste à étudier le polynôme caractéristique. Une autre, plus sophistiquée, consiste à étudier les polynômes de l'endomorphisme. Un concept clé est alors le polynôme minimal qui fournit, par exemple, un critère de diagonalisation particulièrement simple.
Les critères associés à la diagonalisation sont données dans la boite déroulante suivante. Les articles contenant les preuves sont systématiquement cités.
Cas complexe[modifier | modifier le code]

La figure 11 montre que, même dans le cas où le corps est celui des nombres complexes, il reste encore des cas à élucider, celui des endomorphismes qui se situent sur la nappe, mais pas sur la droite des homothéties. Dans le cas des systèmes d'équations différentiels linéaires, il n'intervient que comme un cas limite, dans l'approche de Sylvester, il n'apparaît plus du tout. En revanche dans la théorie des groupes, ce cas est important. Ce type d'endomorphisme permet la représentation des groupes non commutatifs. Si ces groupes sont infiniment différentiable, alors ils permettent la représentation d'un cas important, celui des groupes de Lie nilpotent.
Pour élucider cette problématique, les méthodes utilisées sont celles mises au point par Nelson Dunford. L'outil essentiel consiste à considérer les combinaisons linéaires de puissance de l'endomorphisme. On obtient ainsi un polynôme d'endomorphisme. Ces polynômes forment une structure d'algèbre commutative doté d'un morphismes de l'ensemble des polynômes vers cette algèbre. Cette approche est féconde, on la retrouve aussi dans l'étude du cas où la dimension n'est plus finie. La théorie associée à cette approche se trouve dans l'article Polynôme d'endomorphisme, et l'application au cas traité ici dans Décomposition de Dunford.
Le résultat remarquable est qu'il n'existe dans ce contexte qu'une unique exception structurelle au cas diagonalisable. C'est le cas où l'endomorphisme u à la puissance p, où p est un entier, est égal à 0. On dit alors que l'endomorphisme est nilpotent. On peut considérer par exemple, en dimension 3, si (e1, e2, e3) est une base, l'endomorphisme u défini par u(e1) = e2, u(e2) = e3 et u(e3) = 0. Cet endomorphisme n'est clairement pas nul son polynôme caractéristique est égal à x3 donc la seule valeur propre est 0. Cet exemple est illustré en figure 12.
Camille Jordan a prouvé que dans ce contexte, tout endomorphisme est somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent et qu'ils commutent entre eux. L'application de la théorie des endomorphismes montre que le cas nilpotent dispose d'une représentation matricielle particulièrement simple et trigonale supérieure. Dans le cas général, cette représentation s'appelle la réduction de Jordan, elle démontre aussi que, dans ce cas, toute matrice est semblable à une matrice triangulaire.
Cas réel[modifier | modifier le code]

Sur les réels un polynôme n'admet pas toujours de racine. Dans notre troisième exemple, celui de la rotation de la terre, l'espace est de dimension 3, or tout polynôme du troisième degré possède une racine sur les réels. En conséquence, il existe au moins une droite de vecteurs propres. C'est l'axe des pôles dans notre exemple. En revanche, dans le cas de dimension paire, par exemple la restriction de cette application au plan illustré en bleu sur la figure 13 de l'équateur, l'existence de valeur propre n'est plus garantie. Ici, une analyse géométrique nous montre qu'il est vain de chercher un vecteur propre car la rotation modifie la direction de tous les vecteurs non nuls.
Dans le cas complexe, nous avons vu que seul un terme nilpotent peut interdire la diagonalisation. Dans le cas réel, une fois retranché le terme nilpotent, seules les rotations empêchent la diagonalisation. Il existe alors deux manières de réduire le cas réel.
La première solution consiste à plonger l'endomorphisme dans un espace vectoriel complexe. C'est la solution la plus simple et la plus fréquente. La réduction de l'endomorphisme y est alors plus aisée. Une fois cette réduction réalisée, l'application de cette réduction à des vecteurs réels donne toujours des solutions réelles.
La deuxième solution consiste à affaiblir la réduction. Tout endomorphisme sur les nombres réels est la somme du produit d'un endomorphisme diagonalisable et d'une rotation avec un endomorphisme nilpotent. L'endomorphisme diagonalisable commute avec l'application nilpotente et la rotation. En revanche, l'application nilpotente ne commute pas avec la rotation.
Démonstration dans Réduction d'endomorphisme
Cas d'un module sur un anneau[modifier | modifier le code]
Les définitions n'utilisent pas le fait que K soit un corps commutatif. Ces définitions ont donc encore un sens dans le cas où E n'est pas un espace vectoriel mais un module sur un anneau. Si l'anneau n'est pas commutatif, on parlera alors de valeur propre à droite ou de valeur propre à gauche. Si l'anneau est commutatif, on parlera simplement de valeur propre.
Cas des formes bilinéaires[modifier | modifier le code]

Les endomorphismes sont aussi utilisés pour représenter des formes bilinéaires, qui sont des objets de même nature que les distances euclidiennes. Les valeurs et vecteurs propres prennent dans ce contexte une signification particulière.
Les formes bilinéaires sont des fonctions qui ne sont pas linéaires, mais quadratiques, au sens où la fonction ne s'exprime plus comme une combinaison linéaire de coordonnées, c'est-à-dire un polynôme (à plusieurs variables) de degré 1 en les coordonnées, mais comme un polynôme du second degré en les coordonnées. La distance euclidienne sur l'espace est par exemple obtenue à partir de la forme bilinéaire , expression qui fait effectivement intervenir un polynôme de degré 2.
Certaines propriétés éventuellement vérifiées par les formes bilinéaires, comme la symétrie, les rendent le cas échéant plus faciles à étudier. La distance euclidienne par exemple est symétrique, ainsi la distance d'un point a à un point b est la même que la distance d'un point b à un point a. Un endomorphisme qui représente une forme bilinéaire symétrique est dit autoadjoint.
Ces endomorphismes autoadjoints disposent en fait de propriétés fortes concernant valeurs et vecteurs propres: non seulement ils admettent des vecteurs propres, mais de plus ceux-ci suffisent pour comprendre entièrement l'endomorphisme ; un endomorphisme auto-adjoint est diagonalisable. Ensuite, les vecteurs propres peuvent être choisis avec une propriété forte : il existe une base orthonormale de vecteurs propres. Enfin, pour ce cas particulier, il existe des méthodes de calcul simples et rapides pour obtenir valeurs et vecteurs propres. Cette situation est illustrée graphiquement sur la figure 14. Un endomorphisme autoadjoint transforme la boule unité en un ellipsoïde dont les axes sont les vecteurs propres et les longueurs des demi-axes les valeurs absolues des valeurs propres.
Par ailleurs, la forme bilinéaire initiale décrit ici l'équivalent d'une distance d'un espace géométrique ; l'espace étudié, muni de la forme bilinéaire, est un nouvel espace géométrique. Sylvester montre que les vecteurs et valeurs propres, de l'endomorphisme auto-adjoint associé, sont des invariants, des êtres qui décrivent les grandeurs naturelles et caractéristiques de la géométrie considérée. La signification physique de ces grandeurs dépend du contexte de l'espace étudié. Sylvester a appliqué ce qui précède au principe d'inertie d'un solide indéformable en mécanique et en avait déduit l'existence d'axes de rotation (vecteurs propres) et de constantes d'inertie (valeurs propres) intrinsèques au solide. Les autres exemples d'applications montre qu'il en est de même dans d'autres situations, par exemple en statistique où les composantes principales révèlent la dimension la plus significative d'un sondage, ou la relativité qui montre l'existence d'un invariant, la signature de Sylvester, dans la structure même de la géométrie de notre univers.
Le rôle des vecteurs et valeurs propres est ainsi modifié. Ils ne sont plus des uniquement des outils de calculs nécessaires pour accélérer un algorithme ou pour résoudre un problème technique de résolution d'équation différentielle, ils acquièrent une autonomie propre, et deviennent des invariants constitutifs d'une géométrie. Ils prennent alors des noms spécifiques au domaine d'application ; on parle par exemple d'axe de rotation en mécanique, de composantes principales en statistiques, ou de directions propres dans le cas d'espaces courbes.
La démonstration de l'existence d'une base de vecteurs propres dans le cas des endomorphismes autoadjoints est donnée dans l'article Endomorphisme autoadjoint.
Théorie spectrale[modifier | modifier le code]
Position du problème[modifier | modifier le code]
L'analyse du cas de la dimension finie montre qu'une connaissance des valeurs propres et des espaces de Jordan associés permet une compréhension profonde des endomorphismes. Il est donc naturel d'essayer d'étendre cette approche aux cas d'espaces vectoriels de dimensions non finies.
Ce besoin de généralisation apparaît naturellement en mathématiques. Les espaces deviennent des espaces de fonctions et les endomorphismes les opérateurs différentiels, comme les dérivées, les gradients ou les laplaciens. L'exemple de la corde vibrante est caractéristique d'une approche de cette nature. Dans ce contexte le vocabulaire évolue, on ne parle plus d'endomorphisme mais d'opérateur, on utilise le terme de fonction propre pour désigner un vecteur propre et une telle démarche prend le nom de théorie spectrale. Elle est une branche de ce qui s'appelle l'analyse fonctionnelle.
L'approche spectrale est séduisante à bien des aspects. Analyser non plus les propriétés analytiques des éventuelles solutions, mais la nature même de l'espace géométrique est une approche élégante. Elle offre de nouveaux outils, comme des bases ou des distances pour résoudre des difficultés souvent complexes. Dans le cas de la dimension finie, cette approche apporte des théorèmes puissants, à la fois théoriques et algorithmiques. Joseph Fourier montre qu'il en est parfois de même dans des cas plus généraux, avec l'étude de l'équation de la chaleur ou des cordes vibrantes. David Hilbert confirme la pertinence de la démarche en ouvrant la voie à une théorie spectrale générale.
Difficultés de l'approche[modifier | modifier le code]
Les propriétés géométriques des espaces fonctionnels sont hélas largement plus faibles que celles des espaces de dimension finie. La première différence est la présence d'une base au sens algébrique du terme. En général, il n'est pas possible de construire une famille libre et génératrice de l'espace par combinaison linéaire finie (la démonstration de l'existence d'une telle famille dans le cas général repose sur l'axiome du choix, ce qui interdit toute construction explicite). Même si de telles constructions existent pour certains espaces, tel que l'espace vectoriel des polynômes, ces espaces sont trop étroits pour contenir beaucoup de solutions des équations que l'on cherche à résoudre. Par exemple, la position initiale d'une corde de guitare pincée par le musicien a fort peu de chance d'être dans l'univers des polynômes trigonométriques.
On peut alors généraliser ce type d'espace par une bonne complétude. On obtient ainsi l'espace des séries trigonométriques ou celui des séries entières. Les résultats sont alors de bons candidats pour établir les fondements d'une théorie spectrale. Pour comprendre la géométrie de tels espaces, la topologie devient essentielle. En effet, par construction de l'espace, les solutions apparaissent comme limites de suites. Cependant la topologie cache bien des surprises pour les espaces fonctionnels.
En dimension finie, toutes les normes définissent la même topologie. En fait, il n'existe véritablement qu'une topologie intéressante pour une analyse en vecteurs propres. En dimension infinie, ce n'est plus le cas, la topologie faible par exemple ne possède même plus de distance associée.
La compacité est toujours vraie en dimension finie pour les fermés bornés. Le théorème de compacité de Riesz nous indique que ce n'est jamais le cas si la dimension n'est pas finie. Il devient illusoire de vouloir extraire des sous-suites convergentes pour trouver des vecteurs propres dans le cas général.
Un endomorphisme est toujours continu en dimension finie. Ce n'est plus le cas pour les opérateurs linéaires des espaces fonctionnels. La dérivée, par exemple, ne possède pas cette propriété. Pour s'en assurer, il suffit de considérer la suite des monômes (xn). Sur l'intervalle [0,1], elle est bornée. Or l'image de la suite par la fonction dérivée ne possède plus cette propriété. Un opérateur linéaire entre espaces vectoriels normés est continu si et seulement si c'est un « opérateur borné », c'est-à-dire si l'image de la boule unité est bornée.
Spectre et ensemble de valeurs propres[modifier | modifier le code]
En dimension finie, si un endomorphisme a est surjectif alors il est bijectif. Ainsi, l'application a – λ Id est une bijection si et seulement si λ n'est pas une valeur propre. Ce n'est pas vrai dans le cas général. Considérons par exemple l'espace E des fonctions infiniment dérivables sur l'intervalle [0, 1], et l'opérateur O qui, à la fonction , associe la fonction . Il est borné et ne possède pas de valeur propre. Considérons l'opérateur O – λ Id qui, à la fonction , associe la fonction . Si λ est compris entre 0 et 1, alors O – λ Id n'est pas surjectif car son image ne contient pas de fonctions dont l'image de λ est différente de 0. On parle alors de spectre pour rendre compte de ce phénomène. Le spectre contient toujours l'ensemble des valeurs propres, et en dimension finie, ces deux notions coïncident. Dans notre exemple le spectre est l'intervalle [0, 1] et l'ensemble des valeurs propres est vide.
La définition précise du spectre est la suivante : soit E un espace de Banach et O un opérateur linéaire, alors le spectre est l'ensemble des scalaires λ tel que l'opérateur O – λ Id n'admet pas d'inverse continu. Ces scalaires sont appelés valeurs spectrales, et, comme dit plus haut, ne coïncident pas toujours avec les valeurs propres, sauf en dimension finie.
Décomposition spectrale des opérateurs autoadjoints compacts[modifier | modifier le code]
En dimension finie, le paragraphe sur l'algèbre bilinéaire montre qu'il existe un cas où il est possible de trouver une base de vecteurs propres sans utiliser les polynômes d'endomorphismes. C'est un bon cadre pour une généralisation car la notion de polynôme s'applique mal dans le cas des espaces fonctionnels. L'espace est alors enrichi d'une distance, euclidienne ou hermitienne et l'endomorphisme possède toujours la « bonne » symétrie que l'on appelle autoadjonction. Dans ce contexte, la boule unité est transformée en un ellipsoïde représenté dans la figure 14. Les axes principaux de cet ellipsoïde sont les vecteurs propres et les longueurs de ces demi-axes sont les valeurs propres. Cette approche géométrique a guidé David Hilbert pour établir un résultat important de théorie spectrale, dans le cas de la dimension infinie.
L'espace vectoriel possède une distance euclidienne ou hermitienne. S'il est complet pour cette distance, on dit que c'est un espace de Hilbert. Les séries trigonométriques ou les fonctions définies sur un segment et dont le carré est intégrable forment un espace de Hilbert séparable.
L'opérateur possède une « bonne » symétrie. Elle reste la même que celle de la dimension finie. Il est ici autoadjoint.
Enfin l'opérateur dispose d'une « bonne » propriété de continuité. Le fait qu'il soit borné ne suffit plus. C'est un opérateur compact, cela signifie que l'image de la boule unité est compacte. Une des conséquences est qu'il n'est plus inversible.
Dans ce contexte, alors des résultats analogues à la dimension finie sont établis. Citons par exemple[17] : si T est un opérateur compact autoadjoint sur un espace de Hilbert, alors :
- le spectre de T est compact et contient la valeur 0 ;
- si ce spectre est réduit à {0} alors T est nul ;
- il existe une base hilbertienne de vecteurs propres pour T.
Application à la physique quantique[modifier | modifier le code]

La théorie spectrale constitue la base mathématique de la mécanique quantique. Les vecteurs propres trouvent donc d'innombrables applications dans ce domaine. Par exemple en chimie, l'étude de l'atome d'hydrogène montre que les états stables des électrons sont modélisés par des vecteurs propres dont les valeurs propres correspondent à des états d'énergie.
Dans le contexte de la mécanique quantique, l'unique solution pour décrire la position d'un électron, dans notre exemple celui de l'hydrogène, est l'utilisation d'une fonction d'onde complexe. Le carré du module de cette fonction d'onde peut alors s'interpréter comme la probabilité de présence de l'électron en un point donné de l'espace. L'espace des fonctions d'ondes est un Hilbert séparable, celui des fonctions de notre espace géométrique dans les complexes dont le carré du module est intégrable.
L'équation qui régit cette fonction d'onde (que l'on note ici ΨE) est une version simplifiée de l'équation de Schrödinger :
H est un opérateur linéaire appelé hamiltonien. C'est un opérateur différentiel d'ordre 2. Il correspond à une transformation de Legendre d'un lagrangien. On peut démontrer qu'un tel opérateur est autoadjoint.
E est un scalaire, qui représente le niveau d'énergie de l'électron.
ΨE est l'inconnue de l'équation. C'est donc par définition une fonction propre, elle correspond alors à ce que les chimistes appellent une orbite stable. Les électrons ne peuvent que sauter d'une orbite stable à une autre.
L'équation d'onde qui régit l'électron correspond donc au cadre de la théorie spectrale. Les solutions sont les fonctions propres d'un opérateur linéaire. La géométrie correspond à un contexte favorable, l'espace est un Hilbert séparable et l'opérateur est autoadjoint. On peut par exemple en déduire directement que l'énergie est toujours un réel. En revanche les propriétés de continuité ne sont pas favorables. Par exemple, l'opérateur n'est pas compact. Cette absence de bonne continuité rend la recherche d'orbites stables difficile.
Le cas de l'atome d'hydrogène est un peu particulier. L'opérateur associé correspond à un cas relativement simple. On peut alors approximer aussi précisément qu'on le souhaite les fonctions propres. La figure 15 représente les premières orbites stables de l'atome d'hydrogène. La couleur représente le carré du module de l'orbite, plus elle est claire, plus la densité est forte. Le centre représente le noyau, ici un proton.
Cette approche ne se limite pas à l'atome d'hydrogène, on peut l'utiliser pour d'autres atomes et même des molécules. C'est le travail qu'a réalisé Linus Pauling dans son livre The Nature of the Chemical Bond sur la nature des liaisons chimiques. Le Prix Nobel de chimie, obtenu principalement grâce à cette approche est l'un des plus importants dans la chimie du XXe siècle. La combinaison linéaire des orbites stables permet par exemple, dans le cas des molécules, de mieux décrire des composés insaturés de l'éthylène.
Valeur propre et recherche mathématique[modifier | modifier le code]
Les valeurs propres restent un vaste sujet de recherche dans les mathématiques d'aujourd'hui. Ce sujet couvre aussi bien la recherche fondamentale qu'appliquée et la dimension finie comme le cas général en dimension infinie.
Recherche fondamentale et dimension finie[modifier | modifier le code]
Si dans le cas des corps usuels comme les nombres réels ou complexes, la problématique des valeurs propres est maintenant largement connue, il n'en est pas de même pour les corps plus ésotériques[Quoi ?] ou les anneaux. Dans le cas des corps finis, cette approche offre un regard particulier par exemple sur la cryptologie. D'autres corps comme les p-adiques sont encore largement mal connus[Information douteuse]. Une approche linéaire, avec l'analyse des valeurs propres représente un outil supplémentaire pour l'analyse par exemple de l'anneau des polynômes.
Recherche appliquée et dimension finie[modifier | modifier le code]
L'analyse des valeurs propres et des vecteurs propres représente la meilleure méthode pour la mise au point d'algorithmique rapide de résolution d'équations linéaires. Des critères comme la vitesse de convergence devient alors le premier sujet de recherche. Une technique particulièrement employée consiste à éloigner les valeurs propres pour accélérer la recherche des solutions. Ce secteur, même s'il n'est pas dominé par des mathématiciens au sens théorique du terme, puisqu'il est plus souvent le domaine des mathématiques de l'ingénieur ou de l'informaticien, est toujours en pleine effervescence. Il rejoint les travaux sur l'anneau des nombres di-adiques (représentation binaire finie) et s'ouvre sur une branche des mathématiques difficile. La cryptologie appliquée utilise aussi les représentations linéaires pour offrir des codes multi-clé efficaces et souples. Ici, les corps sont rarement les réels ou les complexes, mais plutôt des corps finis.
Recherche théorique dans le cas général[modifier | modifier le code]
Ce domaine est celui qui rassemble le plus de mathématiciens théoriques. L'algèbre linéaire contient des problèmes encore largement ouverts dans le cas de la dimension infinie. La voie théorique la plus analysée à l'heure actuelle est celle de l'axiomatisation, qui s'incarne dans la géométrie algébrique. Cette approche considère les opérateurs comme éléments d'une algèbre abstraite, bénéficiant d'un certain nombre de propriétés. L'objectif est la compréhension de cette algèbre pour l'appliquer ensuite à des cas particuliers d'algèbre d'opérateurs. Cette approche est particulièrement féconde en mathématiques appliquées à la physique, comme les travaux du mathématicien russe Maxim Kontsevich (médaille Fields 1998), dont les résultats les plus célèbres traitent des déformations quantiques sur les variétés de Poisson à l'aide d'une hiérarchie infinie de structures algébriques généralisant la notion d'algèbre opérant sur un espace vectoriel.
La géométrie algébrique est particulièrement féconde dans le domaine de l'arithmétique. Le mathématicien Laurent Lafforgue a reçu la médaille Fields en 2002 pour ses travaux dans cette branche sur les conjectures de Langlands.
Notes et références[modifier | modifier le code]
- R. Descartes, La Géométrie, 1637
- J. de Witt, commentaire de la version latine de La Géométrie de Descartes, 1660
- (la) C. F. Gauss, Demonstratio nova theorematis omnem functionem algebraicum…, 1799.
- Joseph Fourier, Théorie analytique de la chaleur, [détail des éditions].
- (en) W. R. Hamilton, On a General Method in Dynamics, 1834
- (en) A. Cayley, « Chapters in the analytical geometry of (n) dimensions », Cambridge Math. J., vol. 4, , p. 119-127 (lire en ligne)
- (en) A. Cayley, « On the Theory of Linear Transformations] », Cambridge Math. J., vol. 4, , p. 193–209 (lire en ligne)
- (de) H. G. Grassmann, Die Lineale Ausdehnungslehre – ein neuer Zweig der Mathematik, Leipzig, 1844
- A. L. Cauchy, Mémoire sur les clefs algébriques, 1854
- (en) J. Sylvester, « Additions to the articles in the September number of this journal, “On a new class of theorems,” and on Pascal's theorem », Philos. Mag., 3e série, vol. 37, no 251, , p. 363-370
- J. J. Sylvester, Théorie sur les invariants algébriques[réf. nécessaire], 1852
- (en) A. Cayley, « A Memoir on the Theory of Matrices », Philosophical Transactions of the Royal Society, vol. 148, , p. 17-37 (lire en ligne)
- Camille Jordan, Traité des substitutions et des équations algébriques,
- F. Riesz, « Sur les systèmes orthogonaux de fonctions », CRAS, vol. 144, 1907, p. 615-619
- (de) E. Schmidt, « Entwicklung willkürlicher Funktionen nach Systemen vorgeschriebener », Math. Ann., vol. 63, , p. 433-476 (lire en ligne).
- (de) D. Hilbert, Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, (lire en ligne).
- Pour plus de détails et des démonstrations, voir l'article anglais correspondant.
Sources[modifier | modifier le code]
- Serge Lang, Algèbre [détail des éditions]
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
- Walter Rudin, Analyse fonctionnelle [détail des éditions]
- Richard P. Feynman, Robert B. Leighton et Matthew Sands (en), Le Cours de physique de Feynman [détail de l’édition], vol. 5, Mécanique quantique, Dunod
- (en) Nelson Dunford et Jacob T. Schwartz, Linear Operators, Part I General Theory, Wiley-Interscience, 1988
Liens externes[modifier | modifier le code]
- Eléments propres d'un endomorphisme, site de C. Caignaert, Lycée Colbert, Tourcoing
- Calculatrice de matrices dont éléments propres (outil en ligne de WIMS).
- (en) Calculateur en ligne de valeurs et vecteurs propres
- Autour de la réduction de Jordan, par G. Vial, ENS Cachan (traite le cas réel)
- Réduction des endomorphismes – Réduction de Jordan, par M. Merle, université de Nice
- La naissance de l'algèbre, par Ahmed Djebbar
- (en) John J. O'Connor et Edmund F. Robertson, « History Topics – Abstract linear spaces », sur MacTutor, université de St Andrews.
- (en) John J. O'Connor et Edmund F. Robertson, « Index for the Chronology », sur MacTutor, université de St Andrews.
- Le développement de l'analyse fonctionnelle au début du XXe siècle, par R. Rolland, CNRS



























