Ellipse (mathématiques)
| Ellipse | |
 Représentation d'une ellipse
| |
| Type | Section conique |
|---|---|
| Aire | |
| Périmètre | |
| modifier |
|
En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre : c'est une conique d'excentricité strictement comprise entre 0 et 1. On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple).
Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane.
On retrouve aussi, en première approximation[1], des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites artificiels) en orbite autour d'une étoile ou d’une autre planète. La Terre parcourt approximativement une ellipse dont le Soleil est un foyer.
Les différentes définitions de l'ellipse peuvent conduire, dans certains cas extrêmes à la construction d'un point, d'un segment ou d'un cercle, qui sont alors considérés comme des ellipses dégénérées n'en possédant pas toutes les propriétés géométriques.


Définitions géométriques[modifier | modifier le code]
Section d’un cône[modifier | modifier le code]
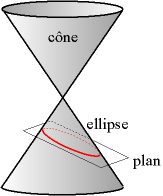
L’ellipse est une courbe plane qui fait partie de la famille des coniques. Elle est obtenue par l’intersection d'un plan avec un cône de révolution (non dégénéré à une droite ou un plan) lorsque ce plan traverse de part en part le cône.
Le cercle est alors un cas particulier de l'ellipse (quand le plan de coupe est perpendiculaire à l'axe du cône, sans passer toutefois par son sommet).
Directrice et foyer[modifier | modifier le code]

Le cadre est l'espace affine euclidien de dimension 2. Soient (d) une droite, F un point n'appartenant pas à (d), e un réel dans ]0,1[. Soit P le plan affine déterminé par (d) et F. On appelle ellipse de droite directrice (d), de foyer F et d'excentricité e l'ensemble des points M du plan P vérifiant :
où d(M, F) mesure la distance du point M au point F et d(M, (d)) = d(M, H) celle de M à la droite (d).
La constante e de proportionnalité des deux distances, appelée excentricité de l’ellipse, est sans dimension ; elle est caractéristique de la forme de l'ellipse, indépendamment de ses isométries (translations et/ou rotations) ou homothéties (de rapport non nul) dans le plan affine, et donc du choix arbitraire de repère orthonormé pour ce plan ; elle détermine tous les autres rapports de distances (et toutes les différences angulaires) mesurés sur l'ellipse.
Notons K le projeté orthogonal de F sur (d). La droite (KF) est alors clairement un axe de symétrie de l'ellipse appelé axe focal. Les points d'intersection de l'ellipse avec son axe focal sont appelés des sommets de l'ellipse. La médiatrice du segment dont les extrémités sont ces deux sommets est également un axe de symétrie de l'ellipse, appelé petit axe de l'ellipse.
Une telle ellipse a donc deux droites directrices, symétriques l'une de l'autre par rapport au petit axe de l’ellipse et deux foyers associés également symétriques par rapport au petit axe.
Une ellipse est également entièrement déterminée par la position de ses foyers et son excentricité, ou bien encore par la position de ses droites directrices (parallèles entre elles), et son excentricité.
En géométrie euclidienne, cette définition de l'ellipse exclut le cercle, le segment de droite et le point.
Définition bifocale de l'ellipse[modifier | modifier le code]

Soient F et F’ deux points distincts du plan. On appelle ellipse de foyers F et F’, l'ensemble des points M du plan vérifiant la propriété suivante :
où 2a est la longueur du grand axe, 2c = d(F, F’) et 2b est la longueur du petit axe (perpendiculaire au grand axe). Cette relation exprime que la somme des distances d'un point M aux foyers est constante et vaut la longueur du grand axe.
Cette définition de l'ellipse permet de tracer un cercle de rayon a lorsque les deux foyers sont confondus mais on ne peut plus alors parler d'axe focal ni de petit axe. Elle permet aussi de tracer un segment de droite lorsque 2a = 2c.
Le théorème de Dandelin permet de placer géométriquement les deux foyers de l'ellipse obtenue par section d'un cône de révolution par un plan, à l'aide des deux sphères inscrites dans le cône et tangentes au plan de section. Un raisonnement analogue permet de prouver que la section d'un cylindre ou d'un hyperboloïde à une nappe par un plan coupant son axe est également une ellipse dont les foyers sont les points de tangence des sphères inscrites dans la surface de révolution et tangentes au plan.
Image d'un cercle par une affinité[modifier | modifier le code]

Soient (C1) un cercle de centre O et de rayon b, (C2) un cercle de centre O et de rayon a (b < a), appelé cercle principal, et (xx’) une droite passant par O. On appelle ellipse de centre O, de demi-grand axe a et de demi-petit axe b l'image du cercle (C2) par l'affinité d'axe (xx’), de direction perpendiculaire à (xx’) et de rapport ba.
Pour construire le point M de l'ellipse, image du point M2 du grand cercle, on construit le point M1 du cercle (C1) situé sur [OM2]. On mène par M2 une perpendiculaire à (xx’) et par M1 une parallèle à (xx’). Les droites se coupent en M. En effet, si m est le projeté orthogonal de M2 sur (xx’), on a, d'après le théorème de Thalès,
Un telle définition de l'ellipse permet de tracer un cercle lorsque le rapport de l'affinité est 1 ou un segment quand le rapport de l'affinité est 0.
Si A est un point de tangence entre l'ellipse et le grand cercle, l'angle est appelé l'anomalie excentrique et peut servir de paramètre simple dans une équation paramétrée de l'ellipse.
Construction par un cercle directeur[modifier | modifier le code]
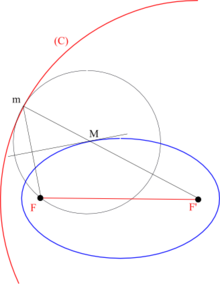
Soient F et F’ deux points distincts, (C) un cercle de centre F’ et de rayon 2a (2a > FF’).
On appelle ellipse de cercle directeur (C) et de foyer F, l'ensemble des centres des cercles tangents intérieurement à (C) et passant par F.
Pour construire le point M sur l'ellipse, centre du cercle tangent à (C) en m, on trace la médiatrice du segment [Fm] : cette médiatrice rencontre le rayon [F’m] en M (le centre du cercle tangent) ; cette médiatrice est aussi une tangente en M de l’ellipse. On peut également obtenir l'ellipse par pliages : sur une feuille de papier, on dessine le cercle directeur et le foyer F et on plie la feuille de papier de manière à superposer un point du cercle avec le foyer F, l'ensemble des pliures obtenues dessine le faisceau des tangentes à l'ellipse.
La figure obtenue est symétrique par rapport au segment [FF’]. L'ellipse possède donc un autre cercle directeur de centre F et de rayon 2a.
Lorsque les deux points F et F’ sont confondus, une telle définition permet de tracer un cercle de centre F et de rayon a. Lorsque le rayon du cercle directeur est exactement égal à la distance FF’, la construction conduit au tracé du segment [FF’] : lorsque le point m est en F, les centres des cercles tangents intérieurement (C) décrivent le segment [FF’], lorsque m est distinct de F, le seul cercle tangent à (C) et passant par F est le cercle (C) lui-même et son centre est F’.
On peut également remarquer que le foyer F se projette orthogonalement sur la tangente en M en un point m’ appartenant au cercle principal de l'ellipse (le cercle de centre O et de rayon a). Plus précisément, l'ensemble des projetés de F sur les tangentes à l'ellipse dessine le cercle principal de l'ellipse[2], ce qui fait du cercle principal la podaire de l'ellipse par rapport à son foyer, et de l'ellipse l'anti-podaire du cercle principal par rapport au foyer.
Hypotrochoïde[modifier | modifier le code]

Si on fait rouler sans glissement un cercle de centre O’ de rayon R à l'intérieur d'un cercle de centre O et de rayon 2R, le lieu parcouru par un point M, solidaire du petit cercle, situé à une distance d du centre O’ parcourt une ellipse. Son centre est O, ses demi-axes sont R + d et |R – d|. L'ellipse est donc un cas particulier d'hypotrochoïde.
Propriétés géométriques[modifier | modifier le code]
Éléments de symétrie[modifier | modifier le code]
« L’axe focal » (FF'), aussi appelé « axe principal », passant par les foyers et perpendiculaire aux directrices, est un axe de symétrie de l'ellipse ; il en est de même pour « l'axe secondaire », perpendiculaire à l'axe focal et passant par le « centre de l'ellipse » au milieu du « segment focal » [FF'].
L'intersection de l'axe focal et de l'axe secondaire, au centre de l'ellipse, est aussi un centre de symétrie.
Les points d'intersection de l'ellipse avec son axe focal sont appelés sommets principaux, ceux de l'ellipse avec son axe secondaire sont les sommets secondaires.
Le segment diamétral qui joint les sommets principaux (respectivement secondaires) en passant par le centre de l'ellipse est appelée « grand axe » (respectivement « petit axe »), comme aussi toute mesure de sa longueur une fois fixée l'unité arbitraire de longueur.
Tangente et bissectrice[modifier | modifier le code]
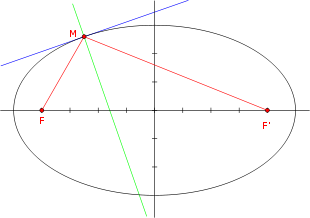
Soit une ellipse dont les foyers sont F et F'. En un point M de cette ellipse, considérons la bissectrice du secteur angulaire (FMF'). Alors, cette bissectrice est perpendiculaire à la tangente en M.
Cette propriété, aussi appelée « propriété de réflexivité », est utilisée en optique géométrique dans les miroirs elliptiques : un rayon lumineux qui passe par un des foyers, lorsqu'il est réfléchi, passe par l'autre foyer. Ainsi, si l'on met une ampoule à un foyer d'un miroir elliptique, le faisceau lumineux se concentre sur l'autre foyer. Elle est également utilisée dans la construction de réflecteur de phare associé à une lentille convergente[3].

On la retrouve en acoustique : dans une pièce de forme elliptique, une personne placée à l'un des foyers peut entendre aisément ce que murmure une personne placée à l'autre. En effet, si la source d'un son se trouve à l’un des foyers, cette propriété assure que tous les sons réfléchis vont converger vers l'autre foyer, compensant la perte d'énergie sonore due à la distance parcourue, par la concentration vers le même point des multiples faisceaux réfléchis. Cependant, cette propriété de convergence spatiale ne suffit pas à assurer que le son perçu soit identique au son émis au foyer source car les signaux suivant différents trajets doivent pour cela arriver en phase à l'autre foyer. Si la nature du milieu est homogène (air ambiant par exemple), la vitesse de propagation du son y est constante, il faut alors pour que les signaux convergent en phase que les distances parcourues selon les différents trajets soient identiques. Or la somme des distances d'un point de l'ellipse aux foyers est constante pour tout point ce qui assure donc la convergence temporelle des signaux. C'est le cumul de ces deux propriétés de l'ellipse qui permet à la fois de comprendre à un foyer des paroles prononcées à l’autre (égale longueur des trajets maintenant les signaux en phase), et de les entendre même si elles ne sont que murmurées (convergence des trajets concentrant l’énergie des signaux). Cette propriété acoustique des voûtes elliptiques est connue au moins depuis le XVIIe siècle[4]. Elle serait à l'origine de la construction de chambres à écho[5], de confessionnaux pour lépreux[6] et expliquerait les qualités sonores des stations de métro parisiennes[6]. La rotonde du Capital Building à Washington et le Mormon Tabernacle à Salt Lake City sont des exemples de cette sorte de galeries[7].
Cette propriété est également utilisée en urologie dans les lithotriteurs extra-corporels : les ondes de choc émises à l'un des foyers de l'ellipse se concentrent, après réflexion sur un réflecteur ellipsoïde, sur l'autre foyer placé judicieusement sur le calcul à détruire[8].
Cercle orthoptique[modifier | modifier le code]

L'ensemble des points M qui « regardent » l'ellipse suivant un angle droit, c'est-à-dire dont partent deux tangentes à l'ellipse perpendiculaires, dessine un cercle de même centre que l'ellipse et de rayon , appelé cercle orthoptique, ou cercle de Monge de l'ellipse[9],[10].
Relations entre les grandeurs[modifier | modifier le code]

Les grandeurs (géométriques ou numériques) d’une ellipse sont :
- la longueur du grand rayon (ou demi-grand axe), généralement notée a ;
- la longueur du petit rayon (ou demi-petit axe), généralement notée b ;
- la distance séparant le centre de l'ellipse et un des foyers, généralement notée c ;
- la distance séparant un foyer F de sa directrice (d) associée, généralement notée h ;
- la distance séparant le centre de l’ellipse et une de ses deux directrices, généralement notée f ;
- l'excentricité de l’ellipse (strictement comprise entre 0 et 1), généralement notée e ;
- le « paramètre » de l’ellipse, généralement noté p, représentant le demi latus rectum (corde parallèle à la directrice et passant par le foyer).
Des relations existent entre ces grandeurs :
- si l’ellipse est définie par son excentricité e et la distance h entre le foyer F et la directrice (d), alors :
- si l’ellipse est donnée par ses rayons a et b où a > b :
- lorsque l’on connait le grand rayon a et l’excentricité e :
- enfin, dans la définition bifocale de l'ellipse où sont connues la longueur 2a et la distance 2c entre les foyers :
Équations caractéristiques[modifier | modifier le code]
Équation cartésienne[modifier | modifier le code]
Dans le repère défini par le demi grand axe et le demi petit axe de l'ellipse, son équation est (si l'axe focal est x) :
- ;
avec a > b > 0. La distance du centre de l'ellipse à l'un des foyers vaut :
et donc l'excentricité vaut :
Si l'axe focal est y alors a et b sont inversés.
Si une ellipse n'est pas centrée à l'origine d'un système de coordonnées, mais que son grand axe et son petit axe restent parallèles aux axes des coordonnées, celle-ci peut être spécifiée par l'équation suivante :
où les paramètres u et v sont les coordonnées du centre de l'ellipse.
Dans le cas où les axes de l'ellipse ne sont plus alignés avec les axes du plan mais tournés d'un angle θ par rapport au repère initial, on obtient l'équation cartésienne suivante :
Comme toute conique, une ellipse possède une équation de la forme :
avec la contrainte B² – 4AC < 0. B étant réel, on en déduit immédiatement que A et C sont non nuls et de même signe (AC > (B/2)² ≥ 0).
On a alors la relation :
Le coefficient B vaut 0 si les axes de l'ellipse sont parallèles à ceux de coordonnées. On a alors :
avec, à un coefficient de proportionnalité près :
- A = 1/a2 ;
- C = 1/b2 ;
- D = –2u/a2 ;
- E = –2v/b2 ;
- F = u2/a2 + v2/b2 – 1.
Réciproquement, une équation de la forme
dans laquelle A, C et sont de même signe, est l'équation d'une ellipse pour laquelle
- ;
- ;
- ;
- .
Forme matricielle[modifier | modifier le code]
Nous pouvons exprimer l'équation cartésienne sous forme matricielle[11] :
où
- ; est la transposée de x ;
- est une matrice symétrique réelle définie positive 2×2, ;
- ; est la transposée de ;
- c= F.
On peut effectuer une rotation de matrice Q et une translation de matrice t, en effectuant un changement de coordonnées :
l'équation devient :
- .
En posant :
on obtient l'équation
- .
On peut alors choisir Q de sorte que soit une matrice diagonale
et de sorte que soit nulle. L'équation cartésienne s'écrit alors
- .
Le centre de l'ellipse a alors pour coordonnées t, et les grand et petit axes valent :
- ;
- .
Équation paramétrique[modifier | modifier le code]
Dans un repère orthonormé du plan affine, dont les vecteurs directeurs sont parallèles aux axes de l'ellipse et où (xC, yC) sont les coordonnées du centre de l'ellipse, un paramétrage possible de l'ellipse est :
Ce paramétrage est périodique, de période 2π, ce qui signifie qu'on peut aussi le restreindre à un intervalle semi-ouvert de longueur minimale égale à cette période, par exemple à . Toute restriction du paramètre à un intervalle fermé de longueur inférieure donne un arc fermé ne parcourant qu'une partie de l'ellipse.
Pour ce paramétrage, le rayon de courbure r au point M de paramètre t est donné par
D'où, en particulier, aux sommets :
Ces deux rayons de courbures permettent une construction approchée de l'ellipse à l'aide de 4 arcs de cercle[12].
Si l'on travaille dans le plan complexe, la représentation paramétrique de l'ellipse de centre C et de demi-axes a et b est
Si maintenant les axes de l'ellipse ne sont plus alignés avec les axes du plan mais tourné d'un angle θ, on obtient l'équation paramétrique en multipliant les coordonnées relatives au centre par la matrice de rotation :
et l'équation paramétrique devient
que l'on peut aussi noter[13] :
avec
- ax = a cos θ ;
- ay = a sin θ ;
- bx = –b sin θ ;
- by = b cos θ.
Équation polaire[modifier | modifier le code]

Dans le repère défini par le foyer F et l'axe focal, avec l'origine des angles du côté opposé de la directrice, l'équation polaire de l'ellipse est :
La 1re forme permet de retrouver la définition de p (le demi latus rectum) avec
La 2e forme permet de voir immédiatement
Remarque : quand l'origine des angles est prise du côté de la directrice.
Dans le repère défini par le centre 0 et l'axe focal, l'équation polaire est :
La 2e forme permet de voir immédiatement et
Paramètres d'une ellipse[modifier | modifier le code]
Le paramétrage d'une ellipse est un point important pour les algorithmes de régression ou de reconnaissance de forme. Une ellipse est décrite par cinq paramètres.
| Définition | Paramètres | Détails |
|---|---|---|
| Foyer, directrice et excentricité |
x, y, a, b, e | Coordonnées (x, y) de F, paramètres de la droite provenant de l'équation cartésienne — pente et ordonnées à l'origine (a, b) — ou bien de l'équation normale — (ρ, θ) —, et excentricité e. |
| Foyers et grand axe |
x1, y1, x2, y2, a | Coordonnées (x1, y1) de F1, (x2, y2) de F2 et longueur du demi grand axe a. |
| Équation cartésienne | B, C, D, E, F ou bien A, B, D, E, F |
l'équation quadratique Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 définit l'ellipse ; A et C sont non-nuls, on peut donc diviser l'équation par l'un des deux pour la normaliser : x2 + Bxy + Cy2 + Dx + Ey + F = 0 ou bien Ax2 + Bxy + y2 + Dx + Ey + F = 0. |
| Équation paramétrique | x, y, a, b, θ ou bien x, y, ax, ay, bx, by |
Coordonnées (x, y) du centre C, longueurs des demi axes a et b, inclinaison θ du grand axe par rapport à l'axe des x. L'équation paramétrique peut aussi s'écrire avec ax = a cos θ, ay = bsin θ, bx = –bsin θ et by = bcos θ. |
Circonférence[modifier | modifier le code]

Le calcul de la longueur d'un arc de l'ellipse de demi grand axe a, de demi petit axe b et d'excentricité e, compris dans le premier quadrant conduit au calcul de
ou à celui de
pour la longueur de l'arc entre le point B (0, b) et le point . Cependant, ces intégrales ne s'expriment pas à l'aide des fonctions classiques (fonctions algébriques, trigonométriques, logarithmes ou exponentielles). Cette rectification, entreprise dès le début du XVIIIe siècle après la mise en place du calcul infinitésimal, conjointement à celle de la lemniscate de Bernoulli, a conduit à une nouvelle classe d'intégrales. Une telle intégrale est appelée intégrale elliptique incomplète de seconde espèce.
La circonférence de l'ellipse, c'est-à-dire son périmètre ou son orbite, s'exprime alors sous forme intégrale par
ou encore
où E est la fonction intégrale elliptique complète de deuxième espèce[14].
Il n'existe pas d'expression simple du résultat final mais des développements en série à convergence plus ou moins rapide dont les premiers sont l'œuvre de Colin Maclaurin de 1742[15] ou Euler en 1749[16] et 1773[17] et des approximations dont celles de Johannes Kepler de 1609[18], Giulio Fagnano de 1750[19] et de Ramanujan du début du XXe siècle.
Développements en séries[modifier | modifier le code]
Le premier développement en série est attribué à Colin Maclaurin mais on en trouve également une démonstration chez Euler en 1749[16]. Il s'obtient en utilisant le développement en série de pour x plus petit que 1 puis en intégrant par récurrence des expressions comme pour Euler[16] ou bien en utilisant les intégrales de Wallis, si c'est la forme trigonométrique qui est privilégiée[20]. Il s'exprime en fonction de a, demi grand axe et e excentricité par :
On peut aussi l'exprimer par :
- ,
où est la série hypergéométrique de Gauss.
Le principal défaut de la série ci-dessus est que sa convergence est très lente pour des excentricités proches de 1, c'est-à-dire pour des ellipses aplaties[21]. Elle reste toutefois utile sur le plan théorique car elle permet de comparer les autres formules donnant des approximations de la circonférence, puisqu'on peut toujours les développer sous forme de série de Taylor, et par différence déterminer la série de Taylor donnant les erreurs relatives commises par ces formules alternatives, en fonction de l'excentricité.
Le second développement intéressant est démontré par Sir James Ivory en 1796[22]. Il porte également le nom de série de Gauss-Kummer pour leur travail consistant à prouver l'équivalence entre plusieurs séries hypergéométriques[17]. C'est un développement symétrique en a et b s'exprimant à l'aide de la quantité :
Cette série a meilleure convergence que celle de Maclaurin sur la totalité de la plage des excentricités mais l'erreur relative pour les ellipses aplaties laisse encore à désirer[23].
On peut également citer la série d'Euler[15] de 1773, développement symétrique en a et b s'exprimant à l'aide de la quantité .
Cette série converge légèrement plus vite que la série de Maclaurin mais moins vite que celle de Gauss-Kummer[24].
Pour les ellipses à forte excentricité, la série d’Arthur Cayley (établie en 1876)[25] offre une meilleure convergence et s'exprime à l'aide de la quantité par :
qui se développe en :
Cette série exacte converge pour toute la plage des excentricités, mais n’a une convergence excellente et bien plus rapide que les séries de Maclaurin et de Gauss-Kummer que pour les excentricités élevées, où elle est également stable numériquement. Dans les évaluations numériques rapides, on peut donc associer cette série de Cayley à la série de Gauss-Kummer plus simple à calculer et convergeant plus rapidement pour les excentricités faibles et modérées, en fixant arbitrairement la coupure entre les deux méthodes à une valeur d’excentricité voisine de 96 % (qui correspond aussi à un rapport d’aspect b/a voisin de 28 % ou une valeur de x voisine de 7,84 %)[25].
Valeurs approchées[modifier | modifier le code]
Une première approximation très simple est présentée par Kepler en 1609[18] et consiste à approcher la circonférence de l'ellipse par la circonférence de deux cercles dont les rayons sont respectivement la moyenne géométrique et la moyenne arithmétique des quantités a et b :
Une seconde approximation date de 1750 et provient de Giulio Carlo Fagnano[19]:
Euler, quant à lui, propose[26] une approximation par excès d'une précision équivalente à celle par défaut obtenue en prenant la moyenne des deux demi-axes :
On trouve également, dans des formulaires, cette approximation quadratique[21], moyenne quadratique des approximations de Kepler et d'Euler :
En exprimant b en fonction de e et en développant en série
on obtient un développement dont les 4 premiers termes correspondent à la série de Maclaurin[27] ; l'erreur commise par les coefficients incorrects des termes de degré supérieur est alors très faible.
À partir du XIXe siècle les formules d'approximations se multiplient [28] , chacun cherchant à trouver des formules simples ayant le maximum de précision. Une mention doit être faite pour les deux formules de Srinivasa Ramanujan de 1914
- Première formule de Srinivasa Ramanujan[29]:
- ,
- où .
- Deuxième formule de Srinivasa Ramanujan[30] :
Ces dernières formules sont très précises pour des excentricités modérées[31]. En revanche pour b = 0, la deuxième formule de Ramanujan conduit à une approximation de π de 22/7[32].
Aire du domaine intérieur à une ellipse[modifier | modifier le code]
Il existe différentes manières de calculer l'aire d'une ellipse. On peut se placer dans le repère porté par les axes où l'équation de l'ellipse s'écrit :
Avec les symétries établies plus haut, il suffit de calculer par exemple l'aire de la portion d'ellipse dans le quart supérieur droit du plan rapporté à ce repère. L'équation de la portion d'ellipse correspondante est :
pour x dans [0,a]. D'où l'aire du quart supérieur droit d'ellipse :
la dernière réécriture obtenue avec le changement de variable de sur . Reste à linéariser pour trouver le quart de l'aire d'une ellipse :
et pour l'aire de toute l'ellipse :
On peut remarquer que pour le cas a = b, on revient à un disque et la formule permet bien de retrouver l'aire du disque.
Tracer une ellipse[modifier | modifier le code]
Méthode des deux points et de la corde : selon la définition bifocale, la somme des distances entre un point de l'ellipse et ses deux foyers F et F' est constante. Ainsi, on plante deux piquets dans le sol (les deux foyers), on prend une corde non élastique de longueur donnée (la somme constante) que l'on attache aux piquets ; le trajet que l'on parcourt en maintenant la corde tendue est une ellipse. On nomme cette technique celle de « l'ellipse du jardinier ».

En dessin industriel, une ellipse est en général un cercle vu en perspective (une pièce est rarement elliptique même si ce n'est pas exclu), ou bien un perçage en biais par rapport à la surface de la pièce.

L'ellipse se représente donc avec les mêmes traits d'axe que pour le cercle. Dans le cas d'un cercle vu en perspective, ces traits d'axe sont inclinés et suivent les directions de référence. Dans le cas d'une forme réellement elliptique, les traits d'axes sont perpendiculaires.

Tracé à main levée, méthode du parallélogramme exinscrit : on a vu ci-dessus qu'une ellipse pouvait être considérée comme un cercle vu en perspective. De même qu'un cercle est inscrit dans un carré, une ellipse est inscrite dans un parallélogramme qui n'est autre que ce carré vu en perspective cavalière (notez qu'il existe une infinité de parallélogrammes circonscrits, il suffit d'en choisir un). On trace d'abord un parallélogramme, on le divise en quatre quartiers selon les parallèles aux côtés passant par les milieux des autres côtés ; dans chaque quartier, on trace un arc passant par les milieux des côtés et tangent aux côtés en ces milieux (certaines caractéristiques de sécantes dans le cercle permettent de trouver d'autres points de passage intermédiaires de ces arcs).

On peut également tracer une ellipse en continu à l'aide d'un instrument mécanique appelé ellipsographe. Il en existe de plusieurs types exploitant chacun une propriété spécifique de l'ellipse.
Tracé à la règle, méthode du parallélogramme[33] : dans un rectangle de dimensions 2a et 4b, on découpe les côtés de longueurs 2a en 2n parties égales et les côtés de longueurs 4b, en 4n parties égales. On trace alors les segments comme sur la figure ci-contre. Leurs points d'intersection sont sur l'ellipse de demi-axes a et b. Le principe en est le suivant : une telle construction appliquée au cas où b = a conduit à tracer des segments perpendiculaires. Leur intersection est donc sur le cercle de diamètre 2a. La figure ci-contre est la déformation par une affinité de rapport b/a, de la figure qui conduit à la construction du cercle. Cette figure conduit donc à la construction de l'ellipse.
Notes et références[modifier | modifier le code]
- voir problème à deux corps et problème à N corps.
- Tauvel 2005, p. 384.
- Les différents projecteurs sur le site educauto.org.
- Voir par exemple le livre d'Athanasius Kircher, Musurgia universalis sive ars magna consoni et dissoni, 1650 tome II,p. 300.
- La chambre des échos de La Chaise Dieu, sur le site de l'Union des professeurs de physique et de chimie.
- Dr Bernard Auriol, Le confessionnal des lépreux.
- Swokowski (trad. Micheline Citta), Analyse, 5e édition, p. 621.
- Association Française d'Urologie, Qu'est-ce que la lithotritie extra corporelle (LEC) ?.
- Voir par exemple Tauvel 2005, p. 387, ou ..
- Romain Bondil et Charles Boubel, « Courbe orthoptique d’une conique » [PDF],
- (en) Walter Gander, Gene H. Golub et Rolf Strebel, « Least-Squares Fitting of Circles and Ellipses », BIT Numerical Mathematics, Springer, vol. 34, no 4, , p. 558-578 (ISSN 0006-3835 et 1572-9125, lire en ligne).
- W Gellert, H. Küstner, M. Hellwich et H. Kästner, Petite encyclopédie des mathématiques, Didier, , p. 197.
- (en) A. S. Aguado et M. S. Nixon, A new Hough transform mapping for ellipse detection, (lire en ligne).
- Attention aux confusions sur la notation de la fonction E ; par exemple dans le programme Mathematica et sur le site Wolfram, on trouve définie une fonction EllipticE similaire, mais différente, , de sorte que la formule à utiliser est alors .
- Almkvist et Berndt 1988, p. 14-598.
- (la) Euler, Animadversiones in rectificationem ellipsis, sur le site [Eulerarchive].
- (en) Numericana, Exact Expansions for the Perimeter of an Ellipse.
- Almkvist et Berndt 1988, p. 15-599.
- Serge Mehl, FAGNANO Giulio Carlo sur le site Chronomath.
- Serge Mehl, Longueur de l'ellipse sur le site Chronomath.
- (en) Numericana, Circumference of an Ellipse.
- (en) James Ivory, A new séries for the rectification of the ellipsis (Almkvist et Berndt 1988, p. 14-598 note 25).
- (en) Numericana, Gauss-Kummer Series.
- (en) Numericana, Euler's Expansion.
- (en)Numericana, Cayley's series.
- (en) Numericana, Euler's formula and the naive formula.
- (en) Numericana, Best quadratic formula.
- Almkvist et Berndt 1988, p. 16-600; 17-601.
- (en) Numericana, Ramanujan (I) & Lindner.
- (en) Numericana, Ramanujan (II).
- À titre d'exemple, Gerard Michon indique dans From Kepler's lower bound to Muir's lower bound, les erreurs pour le calcul d'un méridien terrestre (e proche de 0,082) de l'ordre de mètre pour la première formule et mètre pour la seconde.
- Almkvist et Berndt 1988, p. 18-602.
- (en) Computer Drafting, Rex Bookstore, Inc., Drawing ellipse using parallelogram method - p. 46.
Voir aussi[modifier | modifier le code]
Bibliographie et sources[modifier | modifier le code]
- Patrice Tauvel, Géométrie : Agrégation-2e cycle/master, Dunod,
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
- Méthodes modernes en géométrie de Jean Fresnel
- Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)
- (en) Gert Almkvist et Bruce Berndt, « Gauss, Landen, Ramanujan, the Arithmetic-Geometric Mean, Ellipses, Pi and the Ladies Diary », Amer. Math. Monthly, vol. 95, no 1, (lire en ligne)
- (en) Gerard P. Michon, Perimeter of an Ellipse - Final Answers, sur Numericana.com
Articles connexes[modifier | modifier le code]
- Coniques
- Régression elliptique
- Transformée de Hough > Détection d'ellipses
- Ovale
- Théorème de Marden
- Ellipsographe
- Ellipsoïde
Liens externes[modifier | modifier le code]
- Bernard Gisin, « Propriétés de l'ellipse avec démonstrations » [PDF],
- Sections d'un cône et théorème de Dandelin
- Robert Ferréol, Jacques Mandonnet et Alain Esculier, « Ellipse », sur Encyclopédie des formes mathématiques remarquables,
- (en) Eric W. Weisstein, « Ellipse », sur MathWorld


















![{\displaystyle {\frac {[(x-u)\cos \theta +(y-v)\sin \theta ]^{2}}{a^{2}}}+{\frac {[(x-u)\sin \theta -(y-v)\cos \theta ]^{2}}{b^{2}}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04629a7e0f277b4a97d0fad69633207bc3315eb7)




























































![{\displaystyle {\begin{aligned}L&=2\pi a\sum _{n=0}^{+\infty }\left[{\dfrac {(2n)!}{(2^{n}\cdot n!)^{2}}}\right]^{2}{\frac {-e^{2n}}{2n-1}}\\&=2\pi a\left[1-\left({\dfrac {1}{2}}\right)^{2}e^{2}-\left({\dfrac {1\cdot 3}{2\cdot 4}}\right)^{2}{\dfrac {e^{4}}{3}}-\left({\dfrac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\dfrac {e^{6}}{5}}-\cdots \right]\\&=2\pi a\left[1-{\dfrac {1}{4}}e^{2}-{\dfrac {3}{64}}e^{4}-{\dfrac {5}{256}}e^{6}-{\dfrac {175}{16384}}e^{8}-{\dfrac {441}{65536}}e^{10}\cdots \right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66a0dd669648b9cd1fb3040c38c05b182c42cd2f)



![{\displaystyle {\begin{aligned}L&=\pi (a+b)\cdot {}_{2}{\rm {F}}_{1}\left(-{\frac {1}{2}},-{\frac {1}{2}};1;h\right)\\&=\pi (a+b)\sum _{n=0}^{+\infty }{{\frac {1}{2}} \choose n}^{2}h^{n}=\pi (a+b)\sum _{n=0}^{+\infty }\left[{{\dfrac {(2n)!}{(n!)^{2}}}{\frac {1}{(1-2n)(-4)^{n}}}}\right]^{2}h^{n}\\&=\pi (a+b)\left[1+{\dfrac {h}{4}}+{\dfrac {h^{2}}{64}}+{\dfrac {h^{3}}{256}}+{\dfrac {25h^{4}}{16384}}+{\dfrac {49h^{5}}{65536}}+\cdots \right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fab05cb75f5849814a15e284b8f1e8bd7480f2f5)



![{\displaystyle L=4a\left(1+\sum _{n=1}^{+\infty }{x^{n} \over 2}\left[{(2n)! \over (2^{n}n!)^{2}}\right]^{2}{2n \over 2n-1}\left[\ln \left({16 \over x}\right)-\left(\sum _{k=1}^{n}{4 \over (2k-1)2k}\right)+{2 \over (2n-1)2n}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5bf3726362de38c261ba9b5f66402f22983215d)
![{\displaystyle {\begin{aligned}{L \over 4a}-1&={\frac {x}{4}}\left[\ln \left({\frac {16}{x}}\right)-1\right]+{\frac {3x^{2}}{32}}\left[\ln \left({\frac {16}{x}}\right)-{\frac {13}{6}}\right]+{15x^{3} \over 256}\left[\ln \left({16 \over x}\right)-{\frac {12}{5}}\right]+{175x^{4} \over 4096}\left[\ln \left({16 \over x}\right)-{\frac {1051}{420}}\right]+\cdots \\&\ +{x^{n} \over 2}{1^{2} \over 2^{2}}{3^{2} \over 4^{2}}\cdots {(2n-3)^{2} \over (2n-2)^{2}}{(2n-1) \over 2n}\left[\ln \left({16 \over x}\right)-{4 \over 1\times 2}-{4 \over 3\times 4}-\cdots -{4 \over (2n-3)(2n-2)}-{2 \over (2n-1)(2n)}\right]+\cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bb07734c00f2a085c1694fa4ac57453dffc2639)




![{\displaystyle {\begin{matrix}L\approx 2\pi a{\sqrt {{\frac {3}{4}}+{\frac {1}{4}}{\sqrt {1-e^{2}}}-{\frac {3}{8}}e^{2}}}=2\pi a\left[1-{\frac {1}{4}}e^{2}-{\frac {3}{64}}e^{4}-{\frac {5}{256}}e^{6}-{\frac {89}{8192}}e^{8}-{\frac {231}{32768}}e^{10}\cdots \right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d90747026260c2186d37575c89571b3a5b39d76)
![{\displaystyle L\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]=\pi (a+b)\left[3-{\sqrt {4-h}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7935a073e22593cd2d6bfabb254e47cfcfa9f0)

![{\displaystyle L\approx \pi \left(a+b\right)\left[1+{3h \over 10+{\sqrt {4-3h}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f39694765726b24656a4f82cb10a12f046d7670)



![{\displaystyle [0,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db58baa407ae179d23402f61cb3edcfd7e4fa5b1)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)







