Déterminant (mathématiques)

En mathématiques, le déterminant est une valeur qu'on peut associer aux matrices ou aux applications linéaires en dimension finie. Sur les exemples les plus simples, ceux de la géométrie euclidienne en dimension 2 ou 3, il s'interprète en termes d'aires ou de volumes, et son signe est relié à la notion d'orientation. Il fut initialement introduit en algèbre, pour résoudre un système d'équations linéaires comportant autant d'équations que d'inconnues. Il se révèle être un outil très puissant dans de nombreux domaines. Il intervient ainsi dans l'étude des endomorphismes, la recherche de leurs valeurs propres, les propriétés d'indépendance linéaire de certaines familles de vecteurs, mais aussi dans le calcul différentiel, par exemple dans la formule de changement de variables dans les intégrales multiples.
Comme pour de nombreuses opérations, le déterminant peut être défini par une collection de propriétés (axiomes) qu'on résume par le terme « forme multilinéaire alternée ». Cette définition permet d'en faire une étude théorique complète et d'élargir ses champs d'applications. Le déterminant peut aussi se concevoir comme une généralisation à l'espace de dimension n de la notion d'aire ou de volume orientés.
Un domaine spécifique de l'algèbre est consacré à l'étude du déterminant et de ses généralisations : il s'agit de l'algèbre multilinéaire.
Histoire des déterminants[modifier | modifier le code]
Les déterminants sont introduits en Occident à partir du XVIe siècle par Cardan[1], soit bien avant les matrices, qui n'apparaissent qu'au XIXe siècle. Les Chinois sont cependant les premiers[réf. nécessaire] à utiliser des tableaux de nombres et à appliquer un algorithme maintenant connu sous le nom de procédé d'élimination de Gauss-Jordan.
Premiers calculs de déterminants[modifier | modifier le code]
Dans son sens originel, le déterminant détermine l'unicité de la solution d'un système d'équations linéaires. Il est introduit dans le cas de la taille 2 par Cardan en 1545 dans son Ars Magna, sous forme d'une règle pour la résolution de systèmes de deux équations à deux inconnues[1]. Cette première formule porte le nom de regula de modo.

L'apparition des déterminants de taille supérieure demande ensuite plus de cent ans. Alors que le Japon est coupé du monde extérieur, le Japonais Seki Kōwa et l'Allemand Leibniz en donnent les premiers exemples presque simultanément.
Leibniz étudie de nombreux systèmes d'équations linéaires. En l'absence de notation matricielle, il représente les coefficients inconnus par un couple d'indices : il note ainsi ij pour ai, j. En 1678, il s'intéresse à un système de trois équations et trois inconnues et donne, sur cet exemple, la formule de développement suivant une colonne. La même année, il écrit un déterminant de taille 4, correct aux signes près[2]. Leibniz ne publie pas ses travaux, qui semblent avoir été oubliés avant que les résultats soient redécouverts indépendamment une cinquantaine d'années plus tard.
À la même période, Seki Kōwa publie un manuscrit sur les déterminants, où il énonce une formulation générale difficile à interpréter. Celle-ci semble donner des formules correctes pour des déterminants de taille 3 et 4, et de nouveau des signes erronés pour les déterminants de taille supérieure[3]. La découverte restera sans lendemain, à cause de la coupure du Japon avec le monde extérieur.
Déterminants de taille quelconque[modifier | modifier le code]
En 1748, un traité d'algèbre posthume de Maclaurin relance la théorie des déterminants, avec l'écriture correcte de la solution d'un système de quatre équations et quatre inconnues[4].
En 1750, Cramer formule les règles qui permettent de résoudre un système de n équations et n inconnues, mais sans en donner la démonstration[5]. Les méthodes de calcul des déterminants sont alors délicates, puisque fondées sur la notion de signature d'une permutation[6].
Les mathématiciens s'emparent de ce nouvel objet, avec des articles de Bézout en 1764[7], de Vandermonde en 1771[8] (étonnamment ne donnant pas le calcul du déterminant de la matrice de Vandermonde actuelle[Note 1] ; c'est un exemple célèbre d'illustration de la loi de Stigler). En 1772, Laplace établit les formules de récurrence portant son nom. L'année suivante, Lagrange découvre le lien entre le calcul des déterminants et celui des volumes[9].
Gauss utilise pour la première fois le mot « déterminant », dans les Disquisitiones arithmeticae en 1801. Il l'emploie pour ce que nous qualifions aujourd'hui de discriminant d'une forme quadratique binaire et qui est un cas particulier du déterminant moderne. Il est également près d'obtenir le théorème sur le déterminant d'un produit[10].
Mise en place de la notion moderne de déterminant[modifier | modifier le code]
Cauchy emploie le mot déterminant dans son sens moderne. On peut ainsi lire dans son article de synthèse sur cette question :
« M. Gauss s'en est servi avec avantage dans ses Recherches analytiques [sic] pour découvrir les propriétés générales des formes du second degré, c'est-à-dire des polynômes du second degré à deux ou plusieurs variables, et il a désigné ces mêmes fonctions sous le nom de déterminants. Je conserverai cette dénomination qui fournit un moyen facile d'énoncer les résultats ; j'observerai seulement qu'on donne aussi quelquefois aux fonctions dont il s'agit le nom de résultantes à deux ou à plusieurs lettres. Ainsi les deux expressions suivantes, déterminant et résultante, devront être regardées comme synonymes[11]. »
Elle représente une synthèse des connaissances antérieures, ainsi que des propositions nouvelles comme le fait que l'application transposée ne modifie pas le déterminant ainsi que la formule du déterminant d'un produit. Binet propose également une démonstration cette même année.
En publiant ses trois traités sur les déterminants en 1841 dans le journal de Crelle, Jacobi donne une véritable notoriété à la notion[10]. Pour la première fois, il présente des méthodes de calcul systématiques, sous forme algorithmique. Il devient également possible d'évaluer des déterminants de fonctions avec la naissance du jacobien.
De 1832 à 1844, les travaux de Grassmann, fondent l'algèbre extérieure et donnent un sens plus général aux déterminants au travers de la représentation des grassmanniennes.
Le cadre matriciel est introduit par les travaux de Cayley et Sylvester. Cayley est également l'inventeur de la notation des déterminants par des barres verticales ; il établit la formule de calcul de l'inverse.
La théorie s'étoffe par l'étude de déterminants ayant des propriétés de symétrie particulières et par l'introduction du déterminant dans de nouveaux champs des mathématiques, comme le wronskien pour les équations différentielles linéaires.
En 1867, Lewis Carroll publie An Elementary Treatise on Determinants: With Their Application to Simultaneous Linear Equations and Algebraical Geometry, dans lequel il énonce dix-sept propriétés dont sept sont, d'après lui, originales[12].
Premiers exemples : aires et volumes[modifier | modifier le code]
Les calculs d'aires et de volumes sous forme de déterminants dans des espaces euclidiens apparaissent comme des cas particuliers de la notion générale. Cette vision des déterminants permet une approche plus géométrique de leurs propriétés.
Déterminant de deux vecteurs dans le plan euclidien[modifier | modifier le code]


Soit P le plan euclidien orienté usuel. Le déterminant des vecteurs et est donné par l'expression analytique
ou, de façon équivalente, par l'expression géométrique
dans laquelle est l'angle orienté formé par les vecteurs et .
Propriétés[modifier | modifier le code]
- La valeur absolue du déterminant est égale à l'aire du parallélogramme défini par et (en effet, est la longueur de la hauteur du parallélogramme associée au côté et l'aire du parallélogramme est ).
- Le déterminant est nul si et seulement si les deux vecteurs sont colinéaires (le parallélogramme devient une ligne).
Cette annulation apparaît comme un test de proportionnalité des composantes des vecteurs par produit en croix.
- Le déterminant des vecteurs et est strictement positif si et seulement si la mesure principale de l'angle entre ces deux vecteurs est comprise dans l'intervalle .
- L'application déterminant est bilinéaire : la linéarité par rapport au premier vecteur s'écritet celle par rapport au second vecteur s'écrit

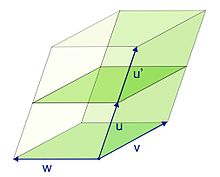
On peut illustrer la linéairité en considérant deux parallélogrammes adjacents, l'un défini par les vecteurs u et v, l'autre par les vecteurs u' et v. L'aire du parallélogramme défini par les vecteurs u+u' et v est égale à la somme des aires des deux parallélogrammes précédents, à laquelle est enlevée l'aire d'un triangle, et ajoutée l'aire d'un autre triangle ; les deux triangles se correspondant par translation. La formule suivante est vérifiée :
Ce dessin correspond à un cas particulier de la formule de bilinéarité puisque les orientations ont été choisies de façon que les aires aient le même signe, mais il aide à en saisir le contenu géométrique.
Généralisation[modifier | modifier le code]
Il est possible de définir la notion de déterminant dans un plan euclidien orienté muni d'une base orthonormale directe B, en utilisant les coordonnées des vecteurs dans cette base. Le calcul de déterminant donne le même résultat quelle que soit la base orthonormale directe choisie pour le calcul.
Déterminant de trois vecteurs dans l'espace euclidien[modifier | modifier le code]
Soit E l'espace euclidien orienté usuel de dimension 3. Le déterminant de trois vecteurs de E est donné par
Ce déterminant porte encore le nom de produit mixte en dimension 3 ; un procédé visuel pour retrouver cette formule est connu sous le nom de règle de Sarrus.
Propriétés[modifier | modifier le code]
- La valeur absolue du déterminant est égale au volume du parallélépipède défini par les trois vecteurs.
- Le déterminant est nul si et seulement si les trois vecteurs sont contenus dans un même plan (parallélépipède « plat »).
- L'application déterminant est trilinéaire : notamment
Comme pour la bilinéarité (vu supra), une illustration géométrique peut s'obtenir en considérant deux parallélépipèdes adjacents, c'est-à-dire possédant une face commune.

Interprétation du signe du déterminant : orientation[modifier | modifier le code]
Dans le plan, le signe du déterminant s'interprète comme le signe de l'angle orienté.
Dans l'espace à trois dimensions, le cube unité sert de référence. Son déterminant vaut un. Un parallélépipède non plat possède un déterminant positif s'il est possible de l'obtenir en déformant continûment, sans jamais l'aplatir, le cube unité.
Le déterminant est au contraire négatif s'il est nécessaire d'appliquer en plus une symétrie, c'est-à-dire si le cube unité ne peut être obtenu qu'en déformant le parallélépipède, puis en observant le résultat de cette déformation dans un miroir.
Approche intuitive du déterminant d'une application linéaire[modifier | modifier le code]
Une application linéaire est une application qui transforme les coordonnées d'un vecteur de manière linéaire. Par exemple dans l'espace de dimension 3, l'application est linéaire si les coordonnées x, y et z d'un vecteur ont pour image x', y' et z' avec :
où a, b, c, d, e, f, g, h et i sont des nombres.

Pour être plus précis, le déterminant d'une application linéaire est un nombre, qui représente un facteur multiplicatif pour les volumes. Si le cube jaune est de volume 1, alors le volume du cube vert est la valeur absolue du déterminant de la première application. La deuxième application a un déterminant nul, ce qui correspond à un aplatissement des volumes.
Le déterminant est positif s'il est possible de déformer continûment le cube jaune pour obtenir le vert. Il est au contraire négatif s'il est nécessaire d'y appliquer en plus une symétrie.
En fait cette propriété n'est pas uniquement vraie pour le cube unité jaune. Tout volume transformé par une application linéaire est multiplié par la valeur absolue du déterminant.
Le déterminant existe pour les applications linéaires d'un espace dans lui-même dans le cas de toutes les dimensions finies. En effet, la notion de volume peut être généralisée : ainsi un « hypercube » ayant ses arêtes de longueur 2 dans un espace euclidien de dimension n aurait un déterminant (sorte d'« hypervolume ») de 2n. En revanche, si l'espace est de dimension infinie, alors le déterminant n'a plus de sens.
Cadre d'utilisation[modifier | modifier le code]
Déterminant et équations linéaires[modifier | modifier le code]
Il existe un cas de calcul numérique très fréquent pour les ingénieurs, les physiciens ou les économistes. Il s'agit de la résolution d'un système d'équations linéaires. Si le système possède autant d'équations que de variables, on peut espérer avoir l'existence et l'unicité d'une solution. Mais ce n'est pas toujours le cas, par exemple en cas de répétition de la même équation, plusieurs solutions conviendront.
Plus précisément, à un système de n équations et n inconnues peut être associé un déterminant. L'existence et l'unicité de la solution est obtenue si et seulement si le déterminant est différent de 0. Ce problème est l'origine historique de l'introduction des déterminants.
Il est possible, non seulement de garantir l'existence et l'unicité de la solution, mais la règle de Cramer fournit un calcul exact de la solution à l'aide de déterminants. Cette méthode n'est ni la plus rapide, ni la plus simple, elle est peu pratiquée pour les calculs explicites, elle est néanmoins utile pour établir certains résultats théoriques, tels que la dépendance par rapport aux paramètres.
Lien avec l'aplatissement des volumes[modifier | modifier le code]
Un système de 3 équations linéaires à 3 inconnues peut être mis sous forme d'une équation linéaire u(X) = B où X = (x, y, z) est un vecteur dont les composantes sont les inconnues du système, u une application linéaire de l'espace et B un vecteur. La résolution du système peut être formulée de façon géométrique : le vecteur B est-il l'image d'un certain vecteur X par u ? Ce dernier est-il unique ? Le déterminant de u apporte la réponse : l'existence et l'unicité sont obtenues si et seulement s'il est non nul.
En reprenant l'exemple du cube, il suffit de considérer un pavage de l'espace par le cube jaune et ses images par des translations selon les trois directions. Une famille de cubes jaunes adjacents remplit alors tout l'espace.
- Si le déterminant n'est pas nul, alors l'image de ce pavage est un pavage de parallélépipèdes de couleur verte, remplissant également tout l'espace. Ceci signifie que tous les vecteurs de l'espace sont des vecteurs images. Notamment, le vecteur B est bien recouvert par l'un des volumes verts. Il est image d'un vecteur X du volume jaune correspondant.
- En revanche, si le déterminant est nul, alors l'image du pavage ne remplit pas l'espace entier. Dans l'exemple du cube aplati rouge, elle ne remplit qu'un plan. Certains vecteurs ne sont jamais atteints, les autres sont l'image de plusieurs vecteurs à la fois.
Plus généralement, pour un système de n équations et n inconnues, le déterminant indique si les images par u remplissent l'espace entier ou seulement un sous-espace.
Déterminant et réduction[modifier | modifier le code]
Les applications linéaires apparaissent non seulement en géométrie élémentaire mais aussi dans de nombreux domaines avancés comme certaines résolutions d'équations différentielles, la définition d'algorithmes rapides ou la résolution de problèmes théoriques. Il est important de comprendre leur comportement.
Un outil d'analyse fécond consiste à répertorier les axes privilégiés, selon lesquels l'application se comporte comme une dilatation, multipliant les longueurs des vecteurs par une constante. Ce rapport de dilatation est appelé valeur propre et les vecteurs auxquels il s'applique vecteurs propres.
Le phénomène d'aplatissement des volumes peut être mesuré par un déterminant. Il correspond au cas où, selon une certaine direction, les vecteurs sont multipliés par un rapport de dilatation égal à 0 (valeur propre nulle). Plus généralement, toutes les valeurs propres peuvent être obtenues par le calcul d'un déterminant à paramètre, appelé polynôme caractéristique.
Déterminant et intégrale multiple[modifier | modifier le code]

Ainsi que le montre l'approche intuitive, le déterminant caractérise la modification de volume d'un parallélépipède par un endomorphisme. L'intégrale multiple est un outil de détermination des volumes dans le cas général. Elle utilise la notion de déterminant dans le cadre du changement de variables. Il prend alors le nom de jacobien. Il peut être imaginé comme le rapport des volumes élémentaires avant et après changement de variables, en usant de la terminologie des éléments différentiels.
Plus précisément, le comportement d'une application différentiable au voisinage d'un point est, au premier ordre, analogue en termes de modification de volume à une application linéaire ayant comme déterminant le jacobien.
Déterminant et amortissement dans les équations différentielles[modifier | modifier le code]

En physique, notamment en mécanique du point, l'équation différentielle linéaire d'ordre deux est fréquente. Elle se présente sous la forme , dans laquelle , , peuvent être des coefficients constants ou plus généralement des fonctions (par exemple du temps). Le terme est appelé facteur d'amortissement.
Cette équation différentielle est associée à un déterminant, appelé wronskien. Il s'interprète comme une aire dans le plan (y, y') appelé espace des phases par les physiciens. Cette aire reste constante au cours du temps si le terme d'amortissement est nul, elle décroît de façon exponentielle s'il est strictement positif. S'il n'est pas toujours possible d'exhiber une solution explicite, le wronskien est toujours calculable.
Le wronskien peut être généralisé à toutes les équations différentielles linéaires.
Définition du déterminant[modifier | modifier le code]
Généralisation à une dimension quelconque[modifier | modifier le code]
Les notions de parallélogramme et de parallélépipède sont généralisées à un espace vectoriel E de dimension finie n sur ℝ[Note 2]. À n vecteurs x1, …, xn de E est associé un parallélotope. Il est défini comme la partie de E formée par l'ensemble des combinaisons des xi à coefficients compris entre 0 et 1
Il convient de voir dans ce parallélotope une sorte de pavé oblique.
Lorsque l'espace est muni d'un produit scalaire, il est possible de définir le volume de ce parallélotope, parfois appelé son hypervolume pour souligner que la dimension de l'espace concerné n'est pas forcément 3. Il vérifie les propriétés suivantes :
- les volumes de deux pavés adjacents par une face s'ajoutent ;
- la multiplication d'un des vecteurs définissant le pavé par une constante induit la multiplication du volume par cette constante ;
- le volume d'un pavé formé par la répétition du même vecteur (ce qui constitue un cas particulier de pavé plat), est nul.
Un changement de produit scalaire sur l'espace E modifie les mesures de longueurs, angles, et par conséquent de volumes. Cependant la théorie des déterminants montrera qu'à une constante multiplicative près, il n'existe qu'une unique méthode de calcul des volumes dans un espace vectoriel de dimension n.
En reprenant un espace vectoriel sans structure particulière, la notion de déterminant a pour objectif de donner un sens intrinsèque au « volume » du parallélotope, sans référence à un produit scalaire par exemple, c'est-à-dire de construire une fonction f, qui à x1, …, xn associe un réel, et vérifie les propriétés précédentes. Une telle application est appelée une forme n-linéaire alternée.
Formes n-linéaires alternées[modifier | modifier le code]
La notion de forme n-linéaire alternée généralise les propriétés précédentes. Elle se définit comme une application de En dans ℝ, qui est :
- linéaire en chaque variable. Ainsi pour des vecteurs x1, …, xn, x'i et deux scalaires a et b
- ;
- alternée, signifie qu'elle s'annule à chaque fois qu'elle est évaluée sur un n-uplet contenant deux vecteurs identiques
- .
L'article détaillé procède à l'étude systématique des formes n-linéaires alternées sur un espace vectoriel de dimension n.
Le résultat principal est la possibilité de ramener le calcul de l'image de à celui d'images des vecteurs de base par n-linéarité. En outre le caractère alterné permet de changer l'ordre des vecteurs, de sorte qu'il suffit de connaître l'image des vecteurs d'une base, pris dans l'ordre, pour connaître f. Remettre les vecteurs dans l'ordre fait intervenir la notion de permutation.
Théorème — L'ensemble des formes n-linéaires alternées sur un espace vectoriel E de dimension n constitue une droite vectorielle.
De plus, si est une base de E, on peut exprimer l'image d'un n-uplet de vecteurs par
avec la i-ème composante de .
Déterminant d'une famille de n vecteurs dans une base[modifier | modifier le code]
Définition
On suppose E muni d'une base .
L'application déterminant en base B est l'unique forme n-linéaire alternée sur E vérifiant , abrégé en ou encore .
On peut se représenter cette quantité comme une sorte de volume de pavé, relativement à la base B.
- Formule de Leibniz

Soient x1, …, xn des vecteurs de E. Il est possible de représenter ces n vecteurs par n matrices colonnes, formant par juxtaposition une matrice carrée X.
Le déterminant de x1, …, xn relativement à la base B vaut alors[Note 3]
.
Cette formule porte parfois le nom de Leibniz. Elle présente peu d'intérêt pour le calcul pratique des déterminants, mais permet d'établir plusieurs résultats théoriques.
En physique, on rencontre souvent la formule de Leibniz exprimée à l'aide du symbole de Levi-Civita, en utilisant la convention d'Einstein pour la sommation des indices :
- .
- Formule de changement de base
Si B et B' sont deux bases de E, les applications déterminants correspondantes sont proportionnelles (avec un rapport non nul)
.
Ce résultat est conforme à l'interprétation en termes de volume relatif.
Déterminant d'une matrice[modifier | modifier le code]
Soit une matrice A = (aij) carrée d'ordre n à coefficients réels. Les vecteurs colonnes de la matrice peuvent être identifiés à des éléments de l'espace vectoriel ℝn. Ce dernier est muni d'une base canonique.
Il est alors possible de définir le déterminant de la matrice A comme le déterminant du système de ses vecteurs colonnes relativement à la base canonique. Il est noté det(A) puisqu'il n'y a pas d'ambiguïté sur la base de référence.
Par définition même, le déterminant dépend de façon linéaire de chaque colonne, et est nul lorsque deux colonnes sont égales. Le déterminant de la matrice identité vaut 1. Enfin il vérifie la formule de Leibniz :
Ce déterminant se note fréquemment avec des barres verticales :
La présentation matricielle apporte une propriété essentielle : une matrice a le même déterminant que sa transposée[Note 4]
- ,
ce qui signifie que le déterminant de A se voit aussi comme le déterminant du système des vecteurs lignes, relativement à la base canonique.
Déterminant d'un endomorphisme[modifier | modifier le code]
Soit u un endomorphisme d'un espace vectoriel de dimension finie. Toutes les matrices représentatives de u ont le même déterminant. Cette valeur commune est appelée déterminant de u.
Le déterminant de u est la valeur par laquelle u multiplie les déterminants de vecteurs
- .
Notamment, les endomorphismes de déterminant 1 conservent le déterminant des familles de vecteurs. Dans le groupe GL(E), ils forment un sous-groupe, noté SL(E) et appelé groupe spécial linéaire. Dans un espace réel de dimension 2, ils se conçoivent comme les applications linéaires conservant les aires orientées, en dimension trois les volumes orientés.
 |
 |
On démontre que ce groupe est engendré par les transvections, dont la matrice dans une base adaptée est de la forme
Par construction même du déterminant des endomorphismes, deux matrices semblables ont le même déterminant.
Propriétés[modifier | modifier le code]
Quitte à effectuer le choix d'une base, il est possible d'énoncer ces propriétés dans le cadre matriciel.
Caractère n-linéaire alterné[modifier | modifier le code]
L'application déterminant sur les familles de vecteurs est une forme multilinéaire alternée. Utiliser cette propriété sur une matrice demande d'exprimer le système de vecteurs colonnes, ou de vecteurs lignes.
Par exemple si la matrice A admet pour colonnes C1..., Cn avec Ci de la forme Ci = aC 'i + C ' 'i
- .
Voici l'effet des opérations élémentaires sur les colonnes de la matrice :
- multiplier une colonne par a, entraîne la multiplication du déterminant par la même valeur ;
- échanger deux colonnes, entraîne la multiplication du déterminant par –1 ;
- ajouter à une colonne une combinaison linéaire des autres colonnes ne modifie pas le déterminant.
Notamment, si toutes les colonnes sont multipliées par a, le résultat est une multiplication par an du déterminant
- .
En revanche, il n'existe pas de formule simple exprimant le déterminant de la somme A + B de deux matrices. En effet, appliquer la multilinéarité par rapport aux colonnes demande d'écrire les colonnes de la somme comme Ai + Bi, puis d'appliquer n fois la propriété de linéarité. Finalement, le déterminant de A + B se scinde en une somme de 2n déterminants hybrides det(A1, A2, B3, A4..., Bn), formés d'un certain nombre de colonnes de A et de B. Cependant, cette somme peut s'écrire assez simplement à l'aide des mineurs de A et de B[14].
Il est possible d'effectuer également des opérations élémentaires sur les lignes, qui ont les mêmes propriétés que les opérations sur les colonnes. Opérer sur les lignes suivant la technique du pivot de Gauss fournit une méthode systématique de calcul des déterminants ; c'est la méthode la plus efficace en règle générale, et on montre[Note 5] que son temps de calcul est de l'ordre de O(n3), c'est-à-dire en gros proportionnelle au cube du nombre de lignes de la matrice.
Propriétés de morphisme et d'annulation[modifier | modifier le code]
Cas d'annulation des déterminants[Note 4]
- Le déterminant d'un système de n vecteurs est nul si et seulement si ce système est lié (et ce, quelle que soit la base de référence).
- Le déterminant d'une matrice (ou d'un endomorphisme) est nul si et seulement si cette matrice (ou endomorphisme) est non inversible.
Ces propriétés expliquent le rôle essentiel que peuvent jouer les déterminants en algèbre linéaire. Ils constituent un outil fondamental pour prouver qu'une famille de vecteurs est une base.
Propriété de morphisme[Note 4]
- .
Ainsi, le déterminant est un morphisme de groupes de GLn(ℝ) dans (ℝ*, ×). En particulier, si est inversible alors .
Il existe une généralisation de la formule de déterminant d'un produit pour le cas de deux matrices rectangulaires : c'est la formule de Binet-Cauchy.
Cofacteurs et formule de récurrence[modifier | modifier le code]
La comatrice — ou matrice des cofacteurs — d'une matrice carrée A de taille n est la matrice carrée de même taille, notée , définie par :
- , où
- est la matrice carrée de taille n déduite de A en remplaçant la j-ème colonne par une colonne constituée uniquement de zéros, sauf un 1 sur la i-ème ligne ;
- est la sous-matrice carrée de taille n – 1 déduite de A en supprimant la i-ème ligne et la j-ème colonne.
Formules de Laplace

On peut calculer le déterminant d'une matrice carrée en fonction des coefficients d'une seule colonne et des cofacteurs correspondants. Cette formule, dite formule de Laplace, permet ainsi de ramener le calcul d'un déterminant de taille n à celui de n déterminants de taille n – 1. Le déterminant de la matrice vide est égal à 1[13].
Les formules de développement sont :
- par rapport à la colonne j : ;
- par rapport à la ligne i :.
Comatrice et calcul de l'inverse
La formule suivante se déduit des formules de Laplace et les inclut :
- .
La matrice transposée de la comatrice est appelée matrice complémentaire de A. Notamment si , alors A est inversible et son inverse est un multiple de la matrice complémentaire. Ce résultat, d'intérêt principalement théorique, ne nécessite « que » des calculs de déterminants :
- .
Variations de la fonction déterminant[modifier | modifier le code]
La formule de Leibniz montre que le déterminant d'une matrice A s'exprime comme somme et produit de composantes de A. Il n'est donc pas étonnant que le déterminant ait de bonnes propriétés de régularité.
Déterminant dépendant d'un paramètre[modifier | modifier le code]
Si est une fonction de classe Ck à valeurs dans les matrices carrées d'ordre n, alors est également de classe Ck.
La formule de dérivation s'obtient en faisant intervenir les colonnes de A
- .
Cette formule est formellement analogue à la dérivée d'un produit de n fonctions numériques.
Application déterminant sur l'espace des matrices[modifier | modifier le code]
- L'application qui à la matrice A associe son déterminant est continue.
Cette propriété a des conséquences topologiques intéressantes : ainsi, dans Mn(ℝ), le groupe GLn(ℝ) est un ouvert et le sous-groupe SLn(ℝ) est un fermé. - Cette application est même indéfiniment différentiable.
Son développement limité à l'ordre 1 au voisinage de A s'écritc'est-à-dire que dans Mn(ℝ) muni de son produit scalaire canonique, la comatrice s'interprète comme le gradient de l'application déterminant.Notamment pour le cas où A est l'identité.Ces formules portent parfois le nom d'identités de Jacobi. Elles sont établies dans l'article « Comatrice ».
Le caractère différentiable permet d'affirmer que GLn(ℝ) et SLn(ℝ) sont des groupes de Lie. - Elle est en fait polynomiale, ce qui fait de GLn(ℝ) une variété algébrique.
- Ce polynôme est irréductible[15].
Généralisation aux espaces vectoriels sur d'autres corps et aux modules[modifier | modifier le code]
Corps commutatifs[modifier | modifier le code]
Les différentes définitions et propriétés de la théorie des déterminants s'écrivent de façon identique dans le cadre des espaces vectoriels complexes et des matrices à coefficients complexes. Il en est de même sur tout corps commutatif, sauf pour le paragraphe « variations de la fonction déterminant » qui n'a alors pas de sens.
Anneaux commutatifs[modifier | modifier le code]
Modules libres de dimensions finies[modifier | modifier le code]
La quasi-totalité de la théorie des déterminants peut encore être étendue aux matrices à coefficients dans un anneau commutatif A et aux modules libres de dimension finie sur A. Le seul point de divergence est la caractérisation de l'annulation des déterminants.
Ainsi une matrice à coefficients dans un anneau commutatif A est inversible si et seulement si son déterminant est inversible dans A.
La question de l'algorithme de calcul du déterminant est à reprendre. En effet, la méthode du pivot de Gauss demande d'effectuer des divisions, ce qui n'est pas possible dans l'anneau A lui-même. Les formules de Leibniz ou de Laplace permettent de faire un calcul sans division, mais restent très coûteuses. Il existe des algorithmes bien plus raisonnables, dont le temps d'exécution est d'ordre O(n4) ; notamment, l'algorithme du pivot de Gauss s'adapte dans le cas d'un anneau euclidien, cette adaptation est décrite dans l'article sur le théorème des facteurs invariants[16].
Modules projectifs de type fini[modifier | modifier le code]
Soient A un anneau commutatif, M un module projectif de type fini et f un endomorphisme de M. Il existe un module N sur A tel que le module P = M ⊕ N est libre de type fini (c'est-à-dire de dimension finie). Soit alors g l'endomorphisme de P défini par g(x, y) = (f(x), y). Alors le déterminant de g ne dépend que de f (et non de N). On l'appelle déterminant de f. Plusieurs des propriétés élémentaires du déterminant s'étendent à ce degré de généralité.
Corps non commutatifs[modifier | modifier le code]
Déterminant de Dieudonné[modifier | modifier le code]
Soient D un corps (non nécessairement commutatif) et (D*)ab l'abélianisé du groupe D* de ses éléments non nuls (c'est le groupe quotient de D* par son groupe dérivé [D*, D*]). Notons θ le morphisme canonique de D* sur (D*)ab.
Soit E un espace vectoriel à droite de dimension finie non nulle sur D. On sait que le groupe linéaire GL(E) est engendré par les transvections et les dilatations de E.
Soit f une dilatation de E. L'ensemble des points fixes de f est un hyperplan vectoriel H de E et il existe une unique droite vectorielle L de E non incluse dans E qui est stable par f. Soit v un vecteur non nul de L. Il existe un unique élément non nul a de D tel que f(v) = va. L'élément θ(a) de (D*)ab ne dépend que de f, et non pas de v. Notons-le ρ(f).
Il existe un unique morphisme de groupes φ de GL(E) dans (D*)ab tel que pour toute transvection f de E, φ(f) = 1 et pour toute dilatation f de E, φ(f) = ρ(f). Pour tout élément f de GL(E), on appelle déterminant de Dieudonné, ou déterminant de f, l'élément φ(f) de (D*)ab.
Pour un endomorphisme f de E qui n'appartient pas à GL(E), le déterminant de Dieudonné de f est défini comme étant 0. En adjoignant 0 à (D*)ab comme élément absorbant (on prolonge la multiplication par 0.g = g.0 = 0 pour tout g dans (D*)ab), on obtient un morphisme[17] surjectif de monoïdes de EndD(E) dans (D*)ab ∪ {0}.
Norme réduite[modifier | modifier le code]
On note D un corps (commutatif ou non) et soit K le centre de D. On suppose que la dimension de D sur K est fini. Soit E un espace vectoriel de dimension finie non nul sur D. La K-algèbre EndD(E) des endomorphismes de E est simple et centrale (son centre est K). Il y a donc une notion de norme réduite Nrd f d'un endomorphisme f de E, c'est alors un élément de K. Si D est commutatif (c'est-à-dire si EndD(E)D = K), la norme réduite d'un élément de EndD(E) = EndK(E) est alors le déterminant.
La norme réduite d'un élément d'une algèbre simple centrale sur K généralise le déterminant d'un endomorphisme d'un espace vectoriel sur un corps commutatif.
Soit L un élément maximal (pour la relation d'inclusion) de l'ensemble des sous-corps commutatif de D (il en existe), et alors L contient D. Par exemple, si D est le corps ℍ des quaternions, on peut prendre pour L le corps ℂ des nombres complexes. Soit alors E0 le L-espace vectoriel sous-jacent à E, et EndD(E) est une sous-K-algèbre unitaire de EndL(E0), et on peut donc considérer tout élément de EndD(E) comme un élément de EndL(E0). Pour tout élément f de EndD(E), la norme réduite de f n'est autre que le déterminant de f considéré comme élément de EndL(E0). Cet élément ne dépend que de f (et non pas de L), et il appartient à K. Si D = ℍ, alors la norme réduite d'un élément de Endℍ(E) est un nombre réel positif ou nul.
Formule de composition[modifier | modifier le code]
Le résultat suivant[18] peut servir à établir des formules de composition sur les normes.
Soient A un anneau commutatif et n2 matrices Mi,j (1 ≤ i, j ≤ n) à coefficients dans A, carrées d'ordre m et qui commutent entre elles. Alors, la matrice par blocs (carrée d'ordre mn)
a même déterminant que la matrice (carrée d'ordre m) D(M1,1… , Mn,n), où D(X1,1… , Xn,n) est le polynôme en les indéterminées Xi,j (homogène de degré n et à coefficients entiers) égal au déterminant de la matrice
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- « La grande notoriété n'est assurée en mathématiques qu'aux noms associés à une méthode, à un théorème, à une notation. Peu importe d'ailleurs que l'attribution soit fondée ou non, et le nom de Vandermonde serait ignoré de l'immense majorité des mathématiciens si on ne lui avait attribué ce déterminant que vous connaissez bien, et qui n'est pas de lui ! » Victor-Amédée Lebesgue, conférence d'Utrecht, 1837.
- Le cas particulier n =0, correspondant à l'espace nul, demande donc le calcul du déterminant d'une famille de 0 vecteurs, c'est-à-dire d'une famille vide ; on prend par convention le déterminant égal à 1 dans ce cas[13].
- Notations : désigne l'ensemble des permutations de et la signature de la permutation (1 pour une permutation paire, -1 pour une permutation impaire).
- Une démonstration est disponible par exemple dans Balac et Sturm 2003, dans Marco et Lazzarini 2012, Cottet-Emard 2005 et dans le chapitre « Déterminant » sur Wikiversité (voir infra).
- Pour plus de détails, se reporter au paragraphe concernant la complexité du temps de calcul.
Références[modifier | modifier le code]
- (en) Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, Londres, I. Grattan-Guinness, , 766-774 p. (ISBN 978-0-415-03785-3), « Determinants ».
- (de) Eberhard Knobloch, Der Beginn der Determinantentheorie : Leibnizens nachgelassene Studien zum Determinantenkalkül, Hildesheim, Gerstenberg, .
- (en) Yoshio Mikami, The Development of Mathematics in China and Japan, New York, Chelsea Pub. Co., 2e éd. (1re éd. 1913).
- (en) Carl Benjamin Boyer, A History of Mathematics, Wiley, .
- (en) Gabriel Cramer, Introduction to the analysis of algebraic curves, .
- (de) Moritz Cantor, Geschichte der Mathematik, Teubner, 1913.
- Étienne Bézout, « Recherches sur le degré des équations résultantes de l’évanouissement des inconnues, et sur le moyens qu’il convient d’employer pour trouver ces équations », Mém. Acad. Roy. Sci Paris, 1764, p. 288-338, aperçu sur Google Livres.
- Alexandre-Théophile Vandermonde, « Mémoire sur l'élimination », Hist. de l'Acad. Roy. des Sciences, Paris, 1772, 2e partie, p. 516-532, aperçu sur Google Livres.
- Joseph-Louis Lagrange, « Nouvelle solution du problème du mouvement de rotation d'un corps de figure quelconque qui n'est animé par aucune force accélératrice », Nouveaux mémoires de l'Académie royale des sciences et des belles-lettres de Berlin, 1773, p. 579-616.
- L'essentiel des informations de ce paragraphe provient de (en) John J. O'Connor et Edmund F. Robertson, « Matrices and determinants », sur MacTutor, université de St Andrews.
- Augustin Louis Cauchy, « Mémoire sur les fonctions qui ne peuvent obtenir que deux valeurs […] », Journal de l'École polytechnique, XVIIe cahier, t. X, Paris, 1815 — Œuvres complètes, série 2, t. 1, p. 91-169 (p. 112-113).
- (en) Charles L. Dodgson, An Elementary Treatise on Determinants, introduction.
- N. Bourbaki, Éléments de mathématique : Algèbre, Chapitres 1 à 3, Springer, (ISBN 978-3-540-33849-9, lire en ligne), III.93.
- (en) Marvin Marcus, « Determinants of sums », The College Mathematics Journal, vol. 21, no 2, 1990, p. 130-135.
- (en) « Slick proof the determinant is an irreducible polynomial », sur math.stackexchange.com, démonstration extraite de (en) Maxime Bôcher, Introduction to Higher Algebra, , p. 176-177.
- Voir aussi : (en) Günter Rote, « Division-Free Algorithms for the Determinant and the Pfaffian: Algebraic and Combinatorial Approaches », sur Université libre de Berlin (document sur les algorithmes sans division).
- Jean Dieudonné, « Les déterminants sur un corps non commutatif », Bulletin de la SMF, vol. 71, , p. 27-45 (DOI 10.24033/bsmf.1345)(note p. 36).
- Bourbaki 2007, p. III.112-113 ; (en) N. Bourbaki, Elements of Mathematics : Algebra I, Chapters 1-3, Springer, (ISBN 978-3-54064243-5, lire en ligne), p. 546-547.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Michael Artin, Algebra [détail de l’édition]
- S. Balac et F. Sturm, Algèbre et analyse : cours de mathématiques de première année avec exercices corrigés, PPUR, (lire en ligne), chap. 11.1 (« Un outil pratique : le déterminant »), p. 459-486
- Henri Cartan, Cours de calcul différentiel : avec exercices, Hermann, coll. « Méthodes », , 355 p. (ISBN 978-2705667023)
- F. Cottet-Emard, Algèbre linéaire et bilinéaire, De Boeck Supérieur, (lire en ligne), chap. 2 (« Déterminants »), p. 23-55
- Pierre Gabriel, Matrices, géométrie, algèbre linéaire [détail des éditions] — Pour une introduction matricielle basée sur les transvections.
- Joseph Grifone, Algèbre linéaire, Cépaduès, , 4e éd., 448 p. (ISBN 978-2854289626)
- Serge Lang, Algèbre [détail des éditions]
- J.-P. Marco et L. Lazzarini, Mathématiques L1 : cours complet avec 1000 tests et exercices corrigés, Pearson, (lire en ligne), chap. 20 (« Déterminants »), p. 529-554
Liens externes[modifier | modifier le code]
- Daniel Perrin, « Lettre à Jean-Luc Dorier sur l'importance des déterminants (à propos de son habilitation) », (version du sur Internet Archive)
- Déterminants, sur le site Mathématique du secondaire de Xavier Hubaut
- Formes multilinéaires et déterminant, sur le site les-mathematiques.net









![{\displaystyle ]0,\pi [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f7fa6582460166e2c164b5be01af3bf4a430820)













![{\displaystyle [\exists i\neq j,x_{i}=x_{j}]\Rightarrow f(x_{1},\dots ,x_{n})=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f036d92e3e6018c2cfcd112964f238f880b5268)

















































