Espace vectoriel
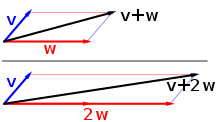
En mathématiques, plus précisément en algèbre linéaire, un espace vectoriel est un ensemble d'objets, appelés vecteurs, que l'on peut additionner entre eux, et que l'on peut multiplier par un scalaire (pour les étirer ou les rétrécir, les tourner, etc.). En d'autres termes, c'est un ensemble muni d'une structure permettant d'effectuer des combinaisons linéaires. Les scalaires sont généralement des nombres réels ou des nombres complexes, ou alors pris dans n'importe quel corps.
Étant donné un corps K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) muni d'une action « compatible » de K (au sens de la définition ci-dessous).
Espace vectoriel[modifier | modifier le code]
Définitions[modifier | modifier le code]
Soit K un corps commutatif[1],[2], comme le corps commutatif des rationnels, celui, , des réels[3] ou celui, , des complexes (on parlera dans ces cas d'espace vectoriel rationnel, réel ou complexe).
Un espace vectoriel sur K, ou K-espace vectoriel, est un ensemble E, dont les éléments sont appelés vecteurs (ou — plus rarement — points[4],[5]), muni de deux lois :
- une loi de composition interne « + » : E2 → E, appelée addition ou somme vectorielle,
- une loi de composition externe à gauche « • » : K × E → E, appelée multiplication par un scalaire,
tel que les propriétés suivantes soient vérifiées :
- 1. (E,+) est un groupe abélien, autrement dit :
- la loi « + » est commutative[N 1],
- elle est associative,
- elle admet un élément neutre, noté 0E, appelé vecteur nul et,
- tout vecteur v a un opposé, noté –v.
- C'est-à-dire que pour tous vecteurs u, v et w de E :
| u + v | = | v + u | u + (v + w) | = | (u + v) + w |
| 0E + v | = | v | u + (–u) | = | 0E |
- 2. La loi « • » vérifie les propriétés suivantes :
- elle est distributive à gauche par rapport à la loi « + » de E et à droite par rapport à l'addition du corps K,
- elle vérifie une associativité mixte (par rapport à la multiplication dans K),
- l'élément neutre multiplicatif du corps K, noté 1K, est neutre à gauche pour •[N 2].
- C'est-à-dire que pour tous vecteurs u, v de E et tous scalaires λ, μ :
| λ•(u + v) | = | (λ•u) + (λ•v) | (λ + µ)•u | = | (λ• u) + (µ • u) |
| (λμ)•u | = | λ•(µ•u) | 1K •u | = | u |
Ces axiomes impliquent que E est non vide et pour tout vecteur u de E et tout scalaire λ[6] :
| λ•u = 0E | ⇔ | (λ = 0K ou u = 0E) | (–λ)•u = –(λ•u) = λ•(–u) |
Les vecteurs (éléments de E) ont été ici écrits avec des lettres latines italiques, mais certains auteurs les notent par des lettres en gras, ou les surmontent d'une flèche.
Exemples[modifier | modifier le code]

Voici quelques exemples d'espaces vectoriels qui servent entre autres en analyse ou en géométrie :
- L'espace nul est l'espace vectoriel sur un corps K comportant un unique élément, qui est nécessairement le vecteur nul. L'espace nul est l'objet initial et l'objet final de la catégorie des espaces vectoriels (en) sur K.
- Tout corps K se présente comme un K-espace vectoriel. L'addition et la multiplication de K fournissent respectivement l'addition vectorielle et la multiplication par un scalaire.
- Plus généralement, l'ensemble des n-uplets d'éléments de K, muni des lois usuelles, forme l'espace vectoriel Kn.
- Les matrices à n lignes et p colonnes à coefficients dans K forment l'espace Mn,p(K).
- Si K est commutatif, toute extension de corps de K, c'est-à-dire tout plongement de K dans un corps L, munit L d'une structure d'espace vectoriel sur K.
- L'ensemble C0(X) des fonctions continues réelles ou complexes définies sur espace topologique X est un espace vectoriel (réel ou complexe).
- L'ensemble des (germes de) solutions d'une équation différentielle linéaire homogène est un espace vectoriel (réel ou complexe).
- L'ensemble des suites numériques satisfaisant une relation de récurrence linéaire est un espace vectoriel réel.
Espaces vectoriels sur un corps non commutatif[modifier | modifier le code]
La définition ci-dessus est celle des espaces vectoriels à gauche sur K. Les espaces vectoriels à droite sur K sont les espaces vectoriels à gauche sur le corps opposé à K. Si le corps K est commutatif, les notions d'espaces vectoriels à gauche et à droite coïncident, et l'on peut alors noter à gauche ou à droite (au choix) la multiplication par un scalaire.
Les notions de la théorie des espaces vectoriels qui ne sont valables, avec les définitions usuelles, que lorsque le corps est commutatif sont notamment celles liées à la multilinéarité (déterminant, trace, produits tensoriels, algèbre extérieure, algèbre sur un corps commutatif) ou aux fonctions polynomiales. Même si l'on ne se sert pas de ces notions, il faut faire attention à divers détails lorsque le corps de base n'est pas supposé commutatif. Par exemple, les homothéties n'existent (en tant qu'applications linéaires) que si le facteur scalaire est central dans le corps, et la multiplication scalaire doit être écrite du côté opposé des applications linéaires (donc avec le scalaire à droite si les applications linéaires sont notées à gauche de leurs arguments).
Combinaison linéaire[modifier | modifier le code]
Les deux opérations sur un espace vectoriel permettent de définir les combinaisons linéaires, c'est-à-dire les sommes finies de vecteurs affectés de coefficients (scalaires). La combinaison linéaire d'une famille (vi)i∈I de vecteurs ayant pour coefficients (λi)i∈I est le vecteur ∑i∈I λivi. Lorsque l'ensemble d'indexation I est infini, il est nécessaire de supposer que la famille (λi)i∈I est à support fini, c'est-à-dire qu'il n'y a qu'un ensemble fini d'indices i pour lesquels λi est non nul.
Sous-espace vectoriel[modifier | modifier le code]

Un sous-espace vectoriel de E est une partie non vide F de E stable par combinaisons linéaires. Muni des lois induites, F est alors un espace vectoriel. L'intersection d'une famille non vide (finie ou infinie) de sous-espaces vectoriels est un sous-espace vectoriel mais l'union, même finie, n'en est pas un en général.
Famille de vecteurs et dimension[modifier | modifier le code]
Indépendance linéaire[modifier | modifier le code]
Une famille (vi)i∈I de vecteurs de E est dite libre (sur K) ou encore les vecteurs de cette famille sont dits linéairement indépendants, si la seule combinaison linéaire des vi égale au vecteur nul est celle dont tous les coefficients sont nuls. Dans le cas contraire, la famille est dite liée et les vi sont dits linéairement dépendants.
Une famille constituée d'un seul vecteur est libre si et seulement si ce vecteur est non nul. Un couple de vecteurs est lié si et seulement si les deux vecteurs sont colinéaires. Si (u, v) est un couple de vecteurs linéairement indépendants, alors (u, v), (u + v, v) et (u, u + v) sont eux aussi des couples de vecteurs non colinéaires, mais la famille (u, v, u + v) est toujours liée.
Sous-espace vectoriel engendré[modifier | modifier le code]
Le sous-espace vectoriel engendré par une famille (vi)i∈I de vecteurs, noté Vect((vi)i∈I), est le plus petit sous-espace (au sens de l'inclusion) contenant tous les vecteurs de cette famille. De manière équivalente, c'est l'ensemble des combinaisons linéaires des vecteurs vi. La famille engendre E, ou encore est génératrice, si le sous-espace qu'elle engendre est E tout entier.
Une famille B de vecteurs de E est une base de E si elle est libre et génératrice ou, ce qui est équivalent, si tout vecteur de E s'exprime de manière unique comme combinaison linéaire des éléments de B. L'existence d'une base pour tout K-espace vectoriel E se déduit du théorème de la base incomplète.
Définition de la dimension[modifier | modifier le code]
Étant donné un espace vectoriel E sur un corps K, toutes les bases de E ont le même cardinal, appelé dimension de E.
- La dimension de l'espace Kn est n.
- Tout espace vectoriel de dimension 1 est appelé droite vectorielle. Tout espace de dimension 2 est appelé plan vectoriel.
Deux espaces vectoriels sur K sont isomorphes (c'est-à-dire reliés par un isomorphisme) si et seulement s'ils sont de même dimension.
Application linéaire[modifier | modifier le code]

Soient E et F deux espaces vectoriels sur un même corps K. Une application f de E vers F est dite linéaire si elle est additive et commute à la multiplication par les scalaires : Autrement dit, f préserve les combinaisons linéaires.
L'ensemble des applications linéaires de E dans F est souvent noté L(E, F). Si K est commutatif, L(E, F) est un sous-espace vectoriel de l'espace des fonctions de E dans F. Toute composée d'applications linéaires est linéaire. L'ensemble L(E, E) des endomorphismes de E se note L(E). Un isomorphisme d'espaces vectoriels est une application linéaire bijective. Un automorphisme est un endomorphisme bijectif. L'ensemble des automorphismes de E est le groupe linéaire GL(E).
Noyau et image[modifier | modifier le code]
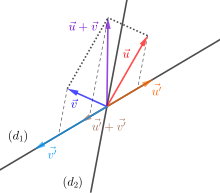
Pour toute application linéaire f de E dans F,
- les vecteurs x de E tels que f(x) = 0 forment un sous-espace vectoriel de E, appelé le noyau de f et noté Ker(f) ;
- les vecteurs f(x) pour x dans E forment un sous-espace vectoriel de F, appelé l'image de f et noté Im(f) ;
- f est
- injective si et seulement si Ker(f) = {0E},
- surjective si et seulement si Im(f) = F ;
- la dimension de Im(f), appelée le rang de f, est inférieure ou égale à celles de E et F. Elle est reliée à celles de E et Ker(f) par le théorème du rang :
+
Le graphe de f est un sous-espace vectoriel de E × F, dont l'intersection avec E × {0} est Ker(f) × {0}.
Forme linéaire[modifier | modifier le code]
Une forme linéaire sur un K-espace vectoriel E est une application linéaire de E dans K. Si K est commutatif, les formes linéaires sur E forment un K-espace vectoriel appelé l'espace dual de E et noté E*. Les noyaux des formes linéaires non nulles sur E sont les hyperplans de E.
Produits et sommes directes[modifier | modifier le code]
La somme F + G de deux sous-espaces vectoriels F et G, définie par coïncide avec le sous-espace vectoriel engendré par F⋃G. Cette construction se généralise à une famille quelconque (non vide) de sous-espaces vectoriels.
La formule de Grassmann relie les dimensions de F et G à celles de leur somme et de leur intersection :
Les deux sous-espaces F et G de E sont dits « en somme directe » lorsque la décomposition de tout vecteur de leur somme F + G en une somme de deux vecteurs, l'un appartenant à F et l'autre à G, est unique (il suffit pour cela que la décomposition de 0E soit unique, c'est-à-dire que F∩G = {0E}). Cette définition se généralise à la somme d'une famille quelconque (non vide) (Fi)i∈I de sous-espaces. Si cette somme est directe alors les Fi sont d'intersection nulle deux à deux mais la réciproque est fausse.
Une somme F + G, lorsqu'elle est directe, est notée F⊕G. Les sous-espaces F et G sont dits supplémentaires (l'un de l'autre) dans E s'ils sont en somme directe et si de plus, cette somme est égale à E. Le théorème de la base incomplète garantit que tout sous-espace vectoriel possède au moins un supplémentaire.
Soit une famille (Ei)i∈I de K-espaces vectoriels. Le produit cartésien ∏i∈I Ei hérite naturellement d'une structure de K-espace vectoriel, appelé espace vectoriel produit.
Les familles à support fini forment un sous-espace vectoriel de ∏i∈I Ei, appelé la somme directe des espaces Ei et noté ⊕i∈I Ei.
Lorsque tous les Ei sont égaux à K, ce produit et cette somme sont respectivement notés KI (l'espace des fonctions de I dans K) et K(I) (le sous-espace des fonctions à support fini, dont la dimension est égale au cardinal de I). Pour I = N, on construit ainsi l'espace KN des suites dans K et le sous-espace K(N) des suites à support fini.
Espace vectoriel quotient[modifier | modifier le code]
Soit F un sous-espace vectoriel de E. L'espace quotient E/F (c'est-à-dire l'ensemble des classes d'équivalence de E pour la relation « u ~ v si et seulement si u – v appartient à F », muni des opérations définies naturellement sur les classes) est un espace vectoriel tel que la projection E → E/F (qui associe à u sa classe d'équivalence) soit linéaire de noyau F.
Tous les sous-espaces supplémentaires de F dans E sont isomorphes à E/F. Leur dimension commune, lorsqu'elle est finie, s'appelle la codimension de F dans E.
Propriétés des espaces vectoriels de dimension finie[modifier | modifier le code]
Soit E un espace vectoriel engendré par un nombre fini m d'éléments.
- La dimension n de E est finie, inférieure ou égale à m.
- Toute famille libre de E a au plus n vecteurs et toute famille génératrice en a au moins n. Pour qu'une famille d'exactement n vecteurs soit une base, il suffit qu'elle soit libre ou génératrice : elle est alors les deux.
- Le seul sous-espace de E de dimension n est E.
- Si K est commutatif, l'espace dual E* de E est également de dimension n, d'après le théorème de la base duale.
- Si K est commutatif et si n ≠ 0, l'ensemble des formes n-linéaires alternées sur E est un espace vectoriel de dimension 1. Ce résultat est à la base de la théorie du déterminant.
- On déduit du théorème du rang que pour toute application linéaire f de E dans un espace de même dimension n,f est surjective ⇔ f est injective ⇔ f est bijective.
- Si K est commutatif, alors l'application de Mm,n(K) dans L(Kn, Km) qui, à toute matrice A, associe l'application linéaire X ↦ AX, est un isomorphisme d'espaces vectoriels. Plus généralement, toute application linéaire entre deux espaces munis chacun d'une base finie est représentable par une matrice.
Structures connexes[modifier | modifier le code]
Structures relatives[modifier | modifier le code]
- Une paire d'espaces vectoriels est la donnée d'un espace vectoriel et d'un sous-espace de celui-ci.
- Plus généralement, un espace vectoriel peut être filtré par la donnée d'une suite croissante ou décroissante de sous-espaces.
- Un drapeau sur un espace vectoriel E de dimension finie est une suite strictement croissante de sous-espaces, de l'espace nul à E.
- Un espace vectoriel réel de dimension finie peut être orienté par le choix d'une orientation sur ses bases.
- Un espace vectoriel gradué est une famille d'espaces vectoriels, généralement indexée par ℕ, ℤ ou ℤ/2ℤ. Un morphisme entre deux tels espaces vectoriels gradués est alors une famille d'applications linéaires qui respecte la graduation.
Structures algébriques[modifier | modifier le code]
- Un module M sur un anneau A est un groupe additif muni d'une loi externe sur M à coefficients dans A, compatible avec l'addition sur M et avec les opérations sur A. Il ne dispose en général ni de base ni de supplémentaires. Un espace vectoriel s'avère être simplement un module sur un corps[7].
- Une algèbre est un espace vectoriel muni d'une multiplication distributive par rapport à l'addition et compatible avec la loi de composition externe.
- Une algèbre de Lie est un espace vectoriel muni d'un crochet de Lie compatible avec la loi de composition externe.
Structures topologiques et géométriques[modifier | modifier le code]
- Un espace affine est un ensemble muni d'une action libre et transitive d'un espace vectoriel.
- Un espace préhilbertien est un espace vectoriel muni d'un produit scalaire.
- Un espace vectoriel euclidien est un espace préhilbertien réel de dimension finie.
- Un espace euclidien est un espace affine dont la direction est un espace vectoriel euclidien.
- Un espace hermitien est un espace préhilbertien complexe de dimension finie. C'est l'analogue complexe de l'espace vectoriel euclidien.
- Un espace vectoriel est dit normé lorsqu'il est muni d'une norme.
- Un espace de Banach est un espace vectoriel normé et complet pour la distance issue de sa norme. Tous les espaces vectoriels préhilbertiens de dimension finie (essentiellement les espaces euclidiens et hermitiens) sont des espaces de Banach.
- Un espace de Hilbert est un espace préhilbertien complet pour la norme issue de son produit scalaire. C'est donc un cas particulier d'espace de Banach.
- La colinéarité de deux vecteurs permet de définir une classe d'équivalence sur les vecteurs non-nuls. Ce classement par colinéarité définit l'espace projectif dit associé à l'espace vectoriel.
- Si K est un corps muni d'une topologie, un espace vectoriel topologique sur K est un K-espace vectoriel muni d'une topologie compatible, c'est-à-dire que l'addition et la multiplication par un scalaire doivent être continues. C'est le cas entre autres des espaces vectoriels normés et des espaces de Fréchet.
- Un fibré vectoriel est une surjection d'un espace topologique sur un autre, telle que la préimage de chaque point soit munie d'une structure d'espace vectoriel compatible continûment avec les structures des préimages des points voisins.
Historique[modifier | modifier le code]

La notion d'espace vectoriel naît conceptuellement de la géométrie affine avec l'introduction des coordonnées dans un repère du plan ou de l'espace usuel. Vers 1636, Descartes et Fermat donnèrent les bases de la géométrie analytique en associant la résolution d'une équation à deux inconnues à la détermination graphique d'une courbe du plan.
Afin de parvenir à une résolution géométrique sans utiliser la notion de coordonnées, Bolzano introduisit en 1804 des opérations sur les points, droites et plans, lesquelles sont les précurseurs des vecteurs[8]. Ce travail trouve un écho dans la conception des coordonnées barycentriques[9] par Möbius en 1827. L'étape fondatrice de la définition des vecteurs fut la définition par Bellavitis du bipoint, qui est un segment orienté (une extrémité est une origine et l'autre un but). La relation d'équipollence, qui rend équivalents deux bipoints lorsqu'ils déterminent un parallélogramme, achève ainsi de définir les vecteurs.
La notion de vecteur est reprise avec la présentation des nombres complexes par Argand et Hamilton, puis celle des quaternions par ce dernier, comme des éléments des espaces respectifs ℝ2 et ℝ4. Le traitement par combinaison linéaire se retrouve dans les systèmes d'équations linéaires, définis par Laguerre dès 1867.
En 1857, Cayley introduisit la notation matricielle, qui permit d'harmoniser les notations et de simplifier l'écriture des applications linéaires entre espaces vectoriels. Il ébaucha également les opérations sur ces objets.
Vers la même époque, Grassmann reprit le calcul barycentrique initié par Möbius en envisageant des ensembles d'objets abstraits munis d'opérations[10]. Son travail dépassait le cadre des espaces vectoriels car, en définissant aussi la multiplication, il aboutissait à la notion d'algèbre. On y retrouve néanmoins les concepts de dimension et d'indépendance linéaire, ainsi que le produit scalaire apparu en 1844. La primauté de ces découvertes est disputée à Cauchy avec la publication de Sur les clefs algébriques dans les Comptes Rendus.
Peano, dont une contribution importante a été l'axiomatisation rigoureuse des concepts existants — notamment la construction des ensembles usuels — a été un des premiers à donner une définition contemporaine du concept d'espace vectoriel[11] vers la fin du XIXe siècle.
Un développement important de ce concept est dû à la construction des espaces de fonctions par Lebesgue, construction qui a été formalisée au cours du XXe siècle par Hilbert et Banach, lors de sa thèse de doctorat en 1920.
C'est à cette époque que l'interaction entre l'analyse fonctionnelle naissante et l'algèbre se fait sentir, notamment avec l'introduction de concepts clés tels que les espaces de fonctions p-intégrables ou encore les espaces de Hilbert. C'est à cette époque qu'apparaissent les premières études sur les espaces vectoriels de dimension infinie.
Translations[modifier | modifier le code]

Sans disposer d'une définition des espaces vectoriels, une approche possible de la géométrie plane se fonde sur l'étude d'un plan affine de Desargues P. Il comporte des points et des droites, avec une relation d'appartenance appelée incidence, dont les propriétés donnent un sens à l'alignement des points et au parallélisme des droites. On appelle homothétie-translation toute transformation de P préservant l'alignement et envoyant toute droite sur une droite parallèle. Hormis l'identité (considérée à la fois comme une homothétie et une translation), une telle transformation fixe au plus un point ; elle est appelée homothétie si elle fixe un point O, qui est alors son centre ; elle est appelée une translation sinon. L'ensemble des homothéties de centre fixé O forment un groupe commutatif pour la loi de composition, indépendant de O à isomorphisme près, noté K*. Il est possible d'adjoindre un élément 0 pour former un corps K, dont la loi d'addition est encore définie à partir de P. Tout scalaire non nul correspond à une unique homothétie de centre O, et on dit que est son rapport. L'ensemble des translations de P forme un K-espace vectoriel, ses lois étant les suivantes :
- La somme vectorielle de deux translations t et t' est leur composée qui est une translation ;
- La multiplication d'une translation t par un scalaire non nul λ de K est la conjugaison de t par une homothétie h de centre quelconque et de rapport λ, autrement dit la transformation , qui est une translation.
Le vecteur nul est l'identité. L'opposé d'un vecteur représenté par une translation t est le vecteur défini par t−1.
Tout ceci se généralise aux espaces affines d'incidence (ou synthétiques) de dimensions (finies ou infinies) supérieures ou égales à 3 (ils sont alors de Desargues). Mais dans ce cas, si le nombre d'éléments des droite est égal à 2, la relation de parallélisme entre droites doit être incluse dans la définition des espaces affines. Donc, il y a intrinsèquement un espace vectoriel « sous-jacent » à tout plan affine de Desargues et à tout espace affine d'incidence.
Ces considérations permettent de faire le lien entre une approche moderne de la géométrie fondée sur l'algèbre linéaire, et une approche axiomatique.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- L'hypothèse de commutativité de « + » est en fait redondante : elle se déduit des autres propriétés, en développant de deux façons différentes (1 + 1)•(u + v) : cf. notes analogues dans les articles « Anneau unitaire » et « Module sur un anneau ».
- Cette condition est nécessaire, comme le montre le contre-exemple suivant. Si on prend par exemple E = K, et que la loi externe est définie comme l'opération toujours nulle (λ•u = 0 pour tout λ de K et tout u de E), alors tous les autres axiomes sont satisfaits sauf celui-ci.
Références[modifier | modifier le code]
- (en) Serge Lang, Algebra, [détail des éditions] : corps défini au chapitre II, espace vectoriel au chapitre III. La théorie des corps fait l'objet des chapitres VII à XII, d'autres notions d'algèbre étant présentées aux chapitres XIII à XVIII.
- Roger Godement, Cours d'algèbre, 1966 : le chapitre 8 porte sur les anneaux et corps, et le chapitre 10 sur les modules et espaces vectoriels.
- (en) Michael Artin, Algebra [détail de l’édition] : le chapitre 3, consacré aux espaces vectoriels, présente d'abord les espaces vectoriels n avant de donner une définition de la structure de corps.
- Dieudonné 1964, p. 31.
- Serge Lang, Algèbre linéaire, vol. 1, Interéditions, chap. 1 et 2.
- Stéphane Balac et Frédéric Sturm, Algèbre et analyse : cours de mathématiques de première année avec exercices corrigés, PPUR, (lire en ligne), p. 302, prop. 8.1.3.
- Lang 1965, p. 85.
- (de) B. Bolzano, Betrachtungen über einige Gegenstände der Elementargeometrie, 1804.
- (de) A. Möbius, Der barycentrische Calcül, 1827.
- (de) H. Grassmann, Die Ausdehnungslehre.
- (it) G. Peano, Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle operazioni della logica deduttiva, 1888.
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (de) Helmut Boseck, Einführung in die Theorie der linearen Vektorräume, 1967
- Jean Dieudonné, Algèbre linéaire et géométrie élémentaire, Hermann,
- (en) Leon Mirsky (en), An Introduction to Linear Algebra, 1955, rééd. 1990 [lire en ligne]
Lien externe[modifier | modifier le code]
(en) John J. O'Connor et Edmund F. Robertson, « Abstract linear spaces », sur MacTutor, université de St Andrews.
Articles connexes[modifier | modifier le code]
- Réduction d'endomorphisme et Diagonalisation (méthodologie pour déterminer des formes normales des opérateurs)
- Tenseur (objet utile en géométrie et en physique)















