Racine carrée de deux
La racine carrée de deux, notée (ou parfois 21/2), est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui-même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10–9 près est :
- √2 ≈ 1,414 213 562.
Le calcul d’une valeur approchée de √2 a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d’extraction de racines carrées. En informatique, ces recherches se sont poursuivies afin d’optimiser ces algorithmes en réduisant les temps de calcul et la consommation de mémoire.
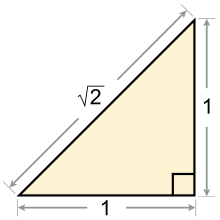
Géométriquement, √2 est le rapport de la diagonale d'un carré sur son côté, dit autrement le rapport de l’hypoténuse d’un triangle rectangle isocèle sur l'un des côtés de l'angle droit, ce qui est un cas particulier du théorème de Pythagore.
Le nombre √2 est connu depuis longtemps : en Mésopotamie, les scribes savaient déjà en calculer une valeur approchée très précise, dans le premier tiers du second millénaire avant notre ère.
Vraisemblablement vers le Ve siècle av. J.-C., les mathématiciens grecs ont montré que la diagonale d'un carré et son côté étaient incommensurables, ce qui revient à dire que √2 est un irrationnel. L'étude de l'incommensurabilité a joué un rôle important dans le développement des mathématiques grecques. Pour les Grecs, ni les fractions, ni les irrationnels ne sont des nombres. Ce pas est franchi par les mathématiciens arabes à l'origine de l'algèbre.
Ce nombre intervient dans des applications de la vie courante :
- les feuilles de papier au format international (ISO 216) ont une proportion longueur/largeur approchée à √2 ;
- en musique, le rapport des fréquences de la quarte augmentée de la gamme tempérée vaut √2 ;
- en électricité, la tension maximale du courant alternatif monophasé domestique vaut √2 fois la tension efficace indiquée (généralement 110 ou 230 V) ;
- en photographie, la suite des valeurs d’ouverture du diaphragme sont les valeurs approchées d’une suite géométrique de raison √2.
Dénomination[modifier | modifier le code]
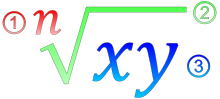
L’expression « racine carrée » est issue de la notation géométrique européenne qui prévalait avant la notation algébrique, et plus particulièrement de l’une des constructions de √2 qui sera présentée à la section consacrée à l'historique ; en effet, les problèmes mathématiques ont souvent été présentés sous forme géométrique avant d’être ramenés à des expressions algébriques.
Le nombre 2 ayant exactement deux racines carrées réelles, √2 et -√2, √2 devrait se prononcer racine carrée positive de 2, ou racine carrée principale de 2. On le prononce simplement racine carrée de 2, voire racine de 2 pour simplifier. Une autre expression correcte, faisant référence au symbole √, est « radical de deux », mais elle est peu courante.
On trouve parfois √2 appelé constante de Pythagore, peut-être à cause d'une légende attribuant la découverte de l'irrationalité de √2 à l'école pythagoricienne[1].
Le symbole a été vu pour la première fois en version imprimée sans la barre horizontale au-dessus des nombres à l’intérieur de la racine en 1525 dans Die Coss de Christoff Rudolff, un mathématicien allemand.
√2 dans la vie courante[modifier | modifier le code]
Format de papier[modifier | modifier le code]

Les formats de papier A, B et C de la norme ISO 216, d’emploi courant hors de l’Amérique du Nord, ont été conçus pour vérifier une propriété remarquable : une feuille coupée en deux parties égales par la largeur, produit deux feuilles semblables à l’original ; c’est-à-dire avec le même rapport longueur/largeur. L’aire étant diminuée d’un facteur 2, ceci n’est possible que si ce rapport vaut √2 ; dans la pratique, les dimensions sont arrondies[2].
Ci-dessous sont données les valeurs approximatives des formats A0 à A5 en fonction de √2.
Valeurs approximatives des dimensions des formats A0 à A5 exprimées en fonction de √2. Dans la pratique, les dimensions sont arrondies. format longueur (m) largeur (m) aire (m2) A0 √√2 √√2⁄√2 1 A1 √√2⁄√2 √√2⁄2 1⁄2 A2 √√2⁄2 √√2⁄(2√2) 1⁄4 A3 √√2⁄(2√2) √√2⁄4 1⁄8 A4 √√2⁄4 √√2⁄(4√2) 1⁄16
Les séries B et C diffèrent de la série A respectivement d’un facteur √√2 (~ 1,19) et √√√2 (~ 1,09).
Les facteurs d’agrandissement de 200 %, 141 %, 71 %, 50 % proposés par les photocopieuses sont des approximations de (√2)n qui permettent le passage à des formats de papier supérieurs ou inférieurs — que ce soit physiquement ou par impression de 2n pages par feuille.
Notons qu'en mathématiques, on note plus volontiers et .
Musique[modifier | modifier le code]
La gamme du tempérament égal se construit ainsi : le rapport de fréquences entre les notes extrêmes de l’octave est 2 ; et la gamme est divisée en douze demi-tons de rapports de fréquence égaux ƒ. Le rapport de fréquences entre la note la plus haute et la plus basse est donc ƒ 12, qui vaut, comme indiqué précédemment, 2. Le demi-ton a ainsi un rapport ƒ = 21/12.
Rapports de fréquences des notes de la gamme tempérée par rapport à la note la plus basse. do do♯ ré ré♯ mi fa fa♯ sol sol♯ la la♯ si do 1 21/12 21/6 21/4 21/3 25/12 √2 27/12 22/3 23/4 25/6 211/12 2
Dans ce système, la quarte augmentée (do–fa♯) et la quinte diminuée (do-sol♭) sont égales et valent six demi-tons ; elles ont un rapport de fréquences de √2. Le chant grégorien utilise cet intervalle, le triton, mais à la fin du Moyen Âge celui-ci est systématiquement évité car jugé trop dissonant. Il reçoit alors le surnom de « Diabolus in Musica».
Électricité[modifier | modifier le code]

En électricité, la tension efficace Ueff d’un courant alternatif sinusoïdal monophasé — par exemple les 110 V ou 220 V du courant domestique — est reliée à l’amplitude de la tension Umax par
- , noté aussi ,
soit, dans la plupart des applications courantes :
Cela est valable plus généralement pour la valeur efficace des grandeurs linéaires d’une onde sinusoïdale. On remarquera aussi que
On parle de bande passante à −3 décibels.
Photographie[modifier | modifier le code]

Les ouvertures des appareils photographiques suivent la séquence normalisée f/1,4, f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22, f/32, etc. Le rapport entre deux ouvertures consécutives est une valeur proche de √2, qui a été choisie de sorte que le rapport de flux lumineux soit dans un rapport 2 (flux = diamètre2). En diminuant d’un « cran » l’ouverture on double le temps de pose nécessaire ou diminue d’un facteur 2 la sensibilité de la pellicule requise[3].
Dans la pratique, l’ouverture indiquée est un arrondi ; l’ouverture réelle peut coller au plus proche de √2[4]. Il existe des subdivisions sur les appareils modernes, souvent dans des rapports ou √21/3.
Lien entre ouverture, diamètre du diaphragme et flux lumineux reçu à pose et sensibilités fixés. Ouverture f/1,4 f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22 f/32 Diamètre d d/√2 d/2 d/2√2 d/4 d/4√2 d/8 d/8√2 d/16 d/16√2 Flux I I/2 I/4 I/8 I/16 I/32 I/64 I/128 I/256 I/512
Dupliquer un carré[modifier | modifier le code]

La question de la duplication d'un carré correspond à la construction d'un carré d'aire double de celle d'un carré donné. On suppose que l'on dispose d'un carré d'aire 1 et l'on cherche à construire un carré d'aire 2. Par définition, le carré d'aire 1 possède un côté de longueur 1 et le carré d'aire 2 possède la même aire que celle de deux carrés d'aire 1.
Il existe deux méthodes simples pour s'en persuader. La plus directe consiste à étudier la figure de gauche[5]. Le carré de côté 1 est composé de deux triangles, celui de côté noté √2 est formé d'exactement quatre triangles du même type, il est donc d'aire double. Une autre manière de se rendre compte du rapport deux entre les aires des carrés de la figure est l'usage du théorème de Pythagore. Un triangle isocèle rectangle de petit côté de longueur 1 possède une hypoténuse de carré égal à 1 + 1 = 2. Cette hypoténuse est la diagonale d'un carré de côté de longueur 1.

L'aire d'un carré s'obtient par multiplication de la longueur du côté par lui-même. La longueur du côté du carré d'aire 2 multiplié par lui-même est donc égal à 2. Par définition de √2, la longueur de ce côté est √2.
Il est en outre possible, à l'aide d'un cercle, de dupliquer le carré sans en changer l'orientation. Dans la figure ci-contre le grand carré a une surface double du petit carré. Il suffit pour s'en convaincre de faire pivoter le petit carré d'un huitième de tour. Le rapport des côtés des deux carrés est donc de √2. La figure de gauche illustrera, pour les mathématiciens futurs la présence de la racine carrée de deux dans le sinus et le cosinus du huitième de tour.
Plus tard, ce tracé séduit de nombreux architectes comme Andrea Palladio dans sa Villa Rotonda ou dans l’Église ronde de Preslav. On le retrouve dans le cloître de la cathédrale de Cahors où la surface de la cour intérieure est égale à la surface de la galerie qui l'entoure[6] ou dans les carnets de Villard de Honnecourt[7].
Preuves d'irrationalité[modifier | modifier le code]
Il existe de nombreuses démonstrations[8] du fait que √2 est irrationnel. Plusieurs d'entre elles n'utilisent que des connaissances arithmétiques très minimales, d'autres se généralisent en remplaçant √2 par √n où l'entier naturel n n'est pas un carré parfait (voir l'article « Irrationnel quadratique »). Certaines sont des reformulations, avec les concepts et le langage mathématiques actuels, de preuves antiques ou supposées telles (cf. § Histoire).
Elles procèdent souvent en utilisant simplement la définition de la négation[9], en supposant que √2 est, au contraire, rationnel, c'est-à-dire qu'il peut s'écrire sous la forme p/q pour certains entiers q > 0 et p, puis en déduisant une contradiction de cette hypothèse √2 = p/q, qui s'écrit aussi p2 = 2q2.
Par parité[modifier | modifier le code]
Soit p le plus petit entier strictement positif tel que p2 soit le double d'un carré, et soit q l'entier positif tel que p2 = 2q2. Alors, p > q (puisque p2 > q2) et p est pair (puisque son carré l'est). En notant p = 2r et en simplifiant par 2, l'équation se réécrit q2 = 2r2, avec 0 < q < p, ce qui contredit la minimalité dans le choix de p.
Une variante consiste à pratiquer une descente infinie à partir d'une (hypothétique) solution p2 = 2q2 : on construit r comme ci-dessus, puis s, t, etc. tels que p2 = 2q2, q2 = 2r2, r2 = 2s2… et p > q > r > s > … , ce qui est absurde puisqu'il n'existe pas de suite infinie strictement décroissante d'entiers positifs.
Autre formulation basée sur la parité : si la fraction p/q est irréductible, p et q ne sont pas pairs simultanément. Comme p/q = √2 donne p2 = 2q2, on en déduit que p est pair puisque son carré l’est (et q est impair) ; p étant pair, on pose p = 2r d’où (2r)2 = 2q2 d’où 4r2 = 2q2 d’où q2 = 2r2 d’où il suit que q serait pair, ce qui contredit soit le fait que q a été signalé impair précédemment, soit que p et q ne sont pas pairs simultanément.
Par soustractions réciproques[modifier | modifier le code]
Soient à nouveau p et q entiers > 0 tels que p/q = √2 avec pq le plus petit possible ou, ce qui revient au même, q le plus petit possible. On déduit de p2 = 2q2 que p(p – q) = p2 – pq = 2q2 – pq = (2q – p)q, d'où en posant[10]
- r = p – q et s = 2q – p :
p/q = s/r, ce qui contredit la minimalité de q, puisque 0 < r < q.
En résumé : soit q le plus petit entier > 0 tel que q√2 est entier, alors q√2 – q est encore un tel entier qui est strictement inférieur à q, d'où une contradiction[11].
(On peut, comme précédemment, transformer ce raisonnement en une descente infinie.)
Par un argument géométrique[modifier | modifier le code]
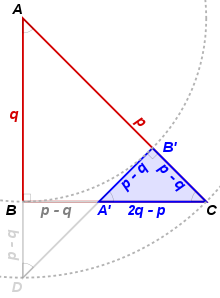
Démontrer l'irrationalité de √2 revient à démontrer que, pour une unité donnée, il n'existe pas de triangle isocèle rectangle dont les côtés sont chacun de longueur un nombre entier d'unité.
Si un tel triangle existe, alors il en existe nécessairement un plus petit dont les côtés sont aussi de longueur entière (sa construction est donnée sur le dessin ci-contre et détaillée ci-dessous). Or si un tel triangle existe, il en existe nécessairement un minimal ayant cette propriété (celui dont le côté de l'angle droit, par exemple, est minimal) d'où une contradiction.
Soit ABC un triangle isocèle rectangle en B et de côtés entiers. Alors, le cercle centré en A de rayon la longueur du petit côté AB coupe l'hypoténuse [AC] en un point B' tel que B'C soit encore de longueur entière, puisque AC et AB' le sont. La perpendiculaire menée en B' à l'hypoténuse [AC] coupe le côté [BC] en A'. Le triangle A'B'C est isocèle rectangle en B', puisque l'angle en B est droit et l'angle en C est celui du triangle d'origine. Les droites (A'B) et (A'B') sont les tangentes issues de A' au cercle de centre A et de rayon AB = AB', et donc A'B = A'B', donc A'B = A'B' = B'C, et A'C est de longueur entière[12]. On peut aussi interpréter la construction comme le pliage du triangle ABC dans lequel on ramène le côté [AB] sur l'hypoténuse[13].
On peut, en explicitant les calculs des côtés du triangle, donner une version purement arithmétique de cette preuve qui est alors celle du paragraphe précédent (prendre p = AC et q = AB = BC).
Par le lemme de Gauss[modifier | modifier le code]
Soit q le plus petit entier > 0 tel que le nombre p := q√2 soit entier, alors q est premier avec p, or il divise p2. Il est donc égal à 1, et p2 = 2, ce qui est impossible. C'est, particularisé à 2, un argument général qui montre que la racine carrée d'un entier qui n'est pas un carré parfait est irrationnelle.
Par le théorème fondamental de l'arithmétique[modifier | modifier le code]
Le couple (p, q) tel que p2 = 2q2 étant cette fois arbitraire (i.e. q non nécessairement minimum), la contradiction vient de ce que dans la décomposition en produit de facteurs premiers, p2 a un nombre pair de facteurs et 2q2 un nombre impair. Une variante est de compter seulement les facteurs égaux à 2. Cet argument, là encore, s'adapte immédiatement à la racine carrée d'un entier qui n'est pas un carré parfait.
Par les congruences[modifier | modifier le code]
Avec p et q premiers entre eux comme plus haut, donc non tous deux divisibles par 3, p2 – 2q2 ne peut pas être nul puisque[14] modulo 3, il est congru à 02 – 2 × (±1)2 ou (±1)2 – 2 × 02 ou (±1)2 – 2 × (±1)2, c'est-à-dire à ±1. (En utilisant la notion d'inverse modulaire, on peut, dans cette méthode, remplacer[14] 3 par n'importe quel nombre premier P tel que 2 n'est pas un carré modulo P, c.-à-d. P congru à 3 ou 5 modulo 8).
Constructions géométriques[modifier | modifier le code]
Construction de √2 à la règle et au compas[modifier | modifier le code]

Comme toute racine carrée de nombre entier, √2 est constructible à la règle et au compas ; a contrario, ce n’est pas le cas de la racine cubique de 2 (c'est le problème de la duplication du cube.
Étant donné un segment AB de longueur unité, voici les différentes étapes pour construire un segment de longueur √2 avec une règle non graduée et un compas :
- Tracer le symétrique B′ de B par rapport à A
- Tracer le cercle C1 de centre A et de rayon AB, il coupe la demi-droite [BA) en B′
- Tracer la médiatrice (AH) de [BB′]
- Tracer le cercle C2 de centre B et de rayon r > AB
- Tracer le cercle C3 de centre B′ et de rayon r, il coupe C2 en deux points, H et H′
- Tracer le segment [AH] il intersecte C1 en un point C.
À cette étape le segment [BC] de longueur √2 est construit.
Construction de √2 au compas seul[modifier | modifier le code]

Comme tout nombre constructible à la règle et au compas, √2 est constructible au compas seul. Les étapes d’une construction possible sont :
- Tracer quatre sommets consécutifs B, G, H, I de l’hexagone régulier de centre A et de sommet B ; ceci permet de construire √3, l’unité étant la longueur AB.
- Tracer le cercle C1 de centre A et de rayon AB ;
- Tracer le cercle C2 de centre B et de rayon AB, il coupe C1 en deux points, soit G l’un d’entre eux ;
- Tracer le cercle C3 de centre G et de rayon AB, il coupe C1 en B et H ;
- Tracer le cercle C4 de centre H et de rayon AB, il coupe C1 en G et I ;
- Construire un triangle rectangle ABC d’hypoténuse BC = √3 (AB = 1) ; C est l’un des deux points tel qu'IC = IG et BC = BH (sachant que IG = BH = √3 > IB/2 = 1).
- Tracer le cercle C5 de centre I et de rayon IG ;
- Tracer le cercle C6 de centre B et de rayon BH (= IG), il coupe C5 en C.
À cette étape le segment [AC] de longueur √2 est construit.
Éléments de démonstration : IC = IG = √3, car d’après le théorème de Pythagore, les hauteurs en I et G des triangles équilatéraux de côté 1, IHA et HAG, qui sont portées par la médiatrice de (H, A), ont pour longueur √3/2. Par construction (A et C sur la médiatrice de BI) (AC) est perpendiculaire à (AI) et le théorème de Pythagore dans IAC donne AC2 = 2..
Histoire[modifier | modifier le code]
La période paléo-babylonienne[modifier | modifier le code]
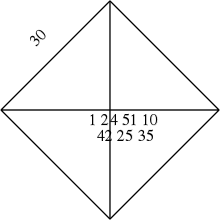
La culture mathématique de la période paléo-babylonienne est avant tout algorithmique. Elle dispose d'un système de numération en notation positionnelle[15]. Certaines tablettes, comme celle notée BM 13901, montrent une bonne connaissance des questions du second degré, probablement traitées à partir de méthodes géométriques simples, par copié-collé d'aires rectangulaires[16]. En plus de disposer de méthodes de résolution, les Babyloniens savent calculer des approximations de racines carrées. La tablette YBC 7289, rédigée dans le premier tiers du second millénaire avant notre ère, donne une approximation de √2, interprétée comme le rapport de la diagonale du carré au côté, sous la forme suivante[17] :
Cette écriture correspond à la meilleure approximation possible de √2 avec quatre chiffres significatifs en numération babylonienne (base 60). L'approximation est précise au millionième. Elle dénote la connaissance d'un algorithme d'approximation de racine carrée, mais on ignore lequel. Il pourrait être de type méthode de Héron[17], encore aujourd'hui l'une des plus efficaces[18].
L'Inde védique[modifier | modifier le code]
Les Śulba-Sūtras, des textes rituels indiens de l'époque védique énoncent des règles géométriques pour la construction d'autels sacrificiels. La date de leur composition est difficile à déterminer, les plus anciens pourraient avoir été composés entre 800 et 500 av. J.-C.[19]. Ils donnent un énoncé de ce que nous appelons maintenant le théorème de Pythagore, y compris le cas particulier de la diagonale du carré, qui permet de doubler son aire[20]. Ils fournissent également une règle pour le calcul de la longueur de cette diagonale en fonction du côté, qui équivaut à une approximation rationnelle de √2 remarquablement précise :
- [20],
soit environ 1,4142157, une valeur précise à un peu plus de 2 millionièmes près. L'un des Śulba-Sūtras, celui de Kātyāyana, précise qu'il ne s'agit que d'une valeur approchée[21]. Les traités ne donnent aucune indication sur la façon dont a été dérivée cette formule[22], même si plusieurs méthodes ont été proposées par les historiens[23].
Grèce antique[modifier | modifier le code]
Les mathématiciens de la Grèce antique ont découvert et démontré l'irrationalité de √2 à une époque qu'il est difficile de déterminer, au plus tard dans les premières décennies du IVe siècle av. J.-C., et vraisemblablement pas avant le Ve siècle av. J.-C.[24]. Ils ne l'exprimaient pas de cette façon : pour eux il n'est pas question d'un nombre √2, mais de rapport (au sens d'une relation) entre la diagonale et le côté du carré, et ils montrent que ceux-ci sont incommensurables, c'est-à-dire que l'on ne peut trouver de segment unité, aussi petit soit-il avec lequel mesurer de façon exacte ces deux longueurs.
La découverte de l'irrationalité, sa date, les circonstances qui ont amené à celle-ci, ses conséquences, la nature des premières démonstrations… tout ceci a suscité beaucoup de travaux chez les historiens[24], sans pour autant que ceux-ci arrivent à un consensus[25].
On ne possède pas de témoignages archéologiques analogues aux tablettes d'argile des Babyloniens, pour les mathématiques de la Grèce antique, mais de textes transmis par la tradition, par copie et recopie. Les premiers à nous être parvenus datent du IVe siècle av. J.-C., dans des œuvres dont les mathématiques ne sont pas l'objectif premier, les écrits de Platon, puis ceux d'Aristote.
Platon et Aristote[modifier | modifier le code]
Dans un passage très connu du Ménon, Platon met en scène Socrate faisant découvrir à un jeune esclave la duplication du carré, par la construction d'un carré sur la diagonale. Socrate veut convaincre Ménon que le jeune esclave retrouve une connaissance qui est déjà en lui. Mais, pour David Fowler qui date le texte de 385 av. J.-C., c'est aussi le premier témoignage substantiel direct de la pratique des mathématiques grecques[26].
La première mention connue de l'incommensurabilité est également due à Platon, dans une œuvre plus tardive, le Théétète, où il décrit Théodore de Cyrène exposant ce qui correspond à l'irrationalité des racines carrées des nombres de 3 à 17 qui ne sont pas des carrés parfaits[27]. On déduit de ce passage que l'irrationalité de √2 est bien connue à l'époque où Platon écrit, voire à celle où Théodore est censé enseigner[28], soit les premières décennies du IVe siècle av. J.-C.
Dans l'Organon, Aristote prend pour exemple de raisonnement par contradiction celui qui conduit à l'incommensurabilité de la diagonale[29], et précise (à deux endroits) que l'hypothèse de la commensurabilité conduit à ce qu'un nombre pair soit égal à un nombre impair[30]. L'indication est imprécise, mais c'est la plus ancienne que l'on ait d'une démonstration. Aristote prend par ailleurs régulièrement pour exemple dans ses œuvres l'incommensurabilité de la diagonale au côté[29],[31].
Euclide[modifier | modifier le code]
Dans les Éléments d'Euclide — le premier traité mathématique qui nous soit parvenu, écrit vers -300 — le traitement de l'incommensurabilité est déjà très élaboré. L'incommensurabilité est définie et traitée au livre X, et la proposition 2 en donne une caractérisation par un procédé de soustractions alternées, l'anthyphérèse, analogue à ce que nous appelons aujourd'hui algorithme d'Euclide en arithmétique (une division peut être vue comme une suite de soustractions) et fraction continue pour les nombres réels[32] (les grandeurs sont incommensurables s'il y a toujours un reste, le procédé continue indéfiniment). La proposition 9 permet le rapport avec les propriétés arithmétiques traitées aux livre VII et livre VIII[33]. Certaines éditions anciennes du livre X donnent bien en appendice une proposition (parfois numérotée 117) qui traite directement l'irrationalité de √2 (l'incommensurabilité de la diagonale du carré et de son côté) par un argument de parité et une descente infinie. Mais celle-ci ne s'intègre pas au reste du texte, elle a pu être ajoutée pour son intérêt historique, et très possiblement après Euclide[34]. Elle semble être postérieure[35] d'une autre démonstration, toujours reposant sur un argument de parité, donnée en commentaire de l'un des passages d'Aristote cité ci-dessus par Alexandre d'Aphrodise au IIe siècle (apr. J.-C.)[36], la plus ancienne complète et vraiment datable qui nous soit parvenue (pour l'incommensurabilité de la diagonale du carré et de son côté)[37].
Hypothèses et reconstructions[modifier | modifier le code]
Ce que l'on peut savoir au sujet de la découverte de l'irrationalité dépend, en plus de ces éléments, de fragments de textes anciens chez des auteurs plus tardifs, en particulier ceux d'une histoire (perdue) d'un élève d'Aristote, Eudème de Rhodes, et plus généralement de textes historiques tardifs, dont la fiabilité n'est pas évidente.
Aussi existe-t-il plusieurs thèses tant pour, le contexte, et les causes de la découverte de l'incommensurabilité, que pour sa ou ses premières démonstrations, les historiens en étant réduits à reconstituer celles-ci, de façon cohérente avec les connaissances (supposées) de l'époque. Ces reconstructions spéculatives développées à la fin du XIXe siècle et au XXe siècle[38], sont loin d'être convergentes et font toujours l'objet de débats[39].
Le pair et l'impair[modifier | modifier le code]
Le plus souvent, √2 (la diagonale du carré) tient le premier rôle, en particulier car une démonstration par parité (le principe en est celui de la première démonstration d'irrationalité ci-dessus) demande pour seule connaissance arithmétique la dichotomie entre nombres pairs et impairs, et peut se reconstituer à partir des connaissances arithmétiques que les historiens jugent pouvoir être celles des mathématiciens grecs du Ve siècle av. J.-C.[40]. Ce serait alors à celle-ci que fait allusion Aristote.
L'anthyphérèse[modifier | modifier le code]
Une autre possibilité est de s'appuyer sur la proposition X, 2 d'Euclide (citée ci-dessus) qui pourrait témoigner d'anciennes démonstrations particulières d'irrationalité par anthyphérèse[41] (soustractions alternées à la façon de l'algorithme d'Euclide). Cependant de telles démonstrations n'apparaissent pas dans Euclide, ni dans aucun texte grec ancien qui nous soit parvenu[42]. Mathématiquement le principe en est celui exposé ci-dessus à la seconde (version arithmétique) et la troisième démonstration (version géométrique)[43]. Le fait de retrouver la même figure dans la version géométrique, montre que le procédé de soustractions réciproques continue indéfiniment donc de conclure par la proposition X, 2. Il faut cependant admettre qu'un segment est divisible à l'infini, et pour cela Euclide appuie sa proposition X, 2 sur la proposition X, 1 (qui traite de la dichotomie), et utilise l'« axiome d'Archimède », attribué à Eudoxe et présent dans les Éléments[44]. Une telle répétition se produit pour tout irrationnel quadratique, elle correspond au développement périodique de sa fraction continue. Cette périodicité rend la caractérisation d'Euclide opératoire pour les rapports correspondant à ces nombres[45]. Dans le cas de √2, elle est immédiate, en une étape, et s'illustre facilement géométriquement. C'est le cas aussi pour la proportion en extrême et moyenne raison (notre nombre d'or), qui est le rapport entre une diagonale et le côté du pentagone, ce qui a conduit certains historiens à envisager que ce rapport, plutôt que √2, ait conduit à la découverte de l'irrationalité[46].
Ces possibilités ne sont pas nécessairement contradictoires, la découverte de l'irrationalité ayant pu se faire à propos de la diagonale du carré et/ou de celle du pentagone par un procédé semblable à l'anthyphérèse et la ou les premières démonstrations procéder par le pair et l'impair[47].
Vers le nombre √2[modifier | modifier le code]

L'histoire de la racine de deux se confond alors avec celle de la racine carrée et plus généralement des irrationnels, en quelques lignes :
- les Grecs, avec le livre V des Éléments, conçoivent ce que nous appelons les rationnels ou les réels comme des proportions, et non pas des nombres[48], théorie « subtile mais non directement opératoire »[49] ;
- alors que la tradition arithmético-algébrique, de Diophante à Al-Khawarizmi, au début du IXe siècle, est restreinte aux nombres rationnels positifs, les mathématiciens du monde arabo-musulman comme Abu Kamil dès le Xe siècle, puis Al-Karaji et Al-Samaw'al, développent une algèbre et un calcul qui comprend les nombres irrationnels, ce dernier et Al-Kashi utilisent des approximations décimales dans le cas des irrationnels[50] ;
- Omar Khayyam développe au XIe siècle une théorie des proportions où celles-ci sont des nombres, même si les incommensurables sont encore appelées impropres, travail que prolonge Nasir al-Din al-Tusi au XIIIe siècle[51] ;
- L'Europe n'assimile ces notions que tardivement, les travaux des mathématiciens du monde arabo-musulman, en particulier ceux d'Al-Tusi, sont connus en Europe au XVIe siècle, qui est une période de polémique pour savoir si les irrationnels méritent le statut de nombre[52], c'est à cette époque que l'usage du symbole √ se répand[53] ;
- même si le débat se poursuit au XVIIe siècle, il finit par se régler avec le développement du calcul algébrique et du calcul infinitésimal, le cadre théorique ne sera cependant défini que dans la seconde moitié du XIXe siècle, concurremment par plusieurs mathématiciens, Dedekind, Weierstrass, Cantor et Méray (voir construction des nombres réels)[54].
Dedekind pourra ainsi affirmer en 1872 quand il publiera son traité sur la construction des réels, que jusqu'alors, jamais l'égalité √2 × √3 = √6 n'avait été démontrée rigoureusement[55].
Autres propriétés[modifier | modifier le code]
Normalité[modifier | modifier le code]
La normalité est un concept se basant sur la distribution des chiffres du développement décimal d’un nombre irrationnel, à savoir si tous les chiffres de 0 à 9 apparaissent dans ce développement et avec la même fréquence. En ce qui concerne √2, on ignore s’il est normal dans le système décimal ou dans toute autre base de numération.
Degré algébrique et degré d'irrationalité[modifier | modifier le code]
√2 est un nombre algébrique de degré 2, dit entier quadratique, car solution de l’équation polynomiale du second degré à coefficients entiers x2 − 2 = 0 et de monôme dominant de coefficient égal à 1, mais d’aucune de degré 1 de par son irrationalité. On sait ainsi qu’il est difficilement approchable par une suite rationnelle pn/qn ; l’erreur est au mieux en
Comme pour tout nombre algébrique irrationnel, sa mesure d'irrationalité est 2.
Développement en fraction continue[modifier | modifier le code]
La partie entière de √2 est 1 et sa partie décimale est donc √2 – 1, soit encore 11 + √2. On peut écrire ce résultat sous la forme :
En remplaçant √2 dans le membre de droite par 1 + 11 + √2, on obtient successivement
Ceci fournit le développement en fraction continue périodique de √2

ainsi que quelques valeurs approchées de ce nombre : 3/2, 7/5, 17/12
√2 est relié à un certain nombre de développements en fractions continues périodiques, par propriété des entiers quadratiques.
Pour a, b entiers strictement positifs tels que a2 − 2b2 = –1, on a le développement suivant
Ce développement se note couramment de manière plus concise :
- b√2 = [a ; 2a, 2a, 2a…].
On en tire les valeurs suivantes de √2 :
- √2 = 1/5 × [7 ; 14, 14, 14…],
- √2 = 1/29 × [41 ; 82, 82, 82…].
Plus généralement, pour a, b entiers strictement positifs tels que a2 − 2b2 = k, on a la fraction continue généralisée suivante :
que l'on note sous forme plus concise
- b√2 = [a ; −k, 2a ; −k, 2a ; −k, 2a ;…]
On en déduit les quelques développements de √2 suivants :
- √2 = 1/2 × [3 ; −1, 6 ; −1, 6 ; −1, 6 ;…]
- √2 = 1/12 × [17 ; −1, 34 ; −1, 34 ; −1, 34;…]
- √2 = 1/70 × [90 ; −1, 180 ; −1, 180 ; −1, 180;…]
Éléments de démonstration : soit la suite (un) définie par la relation de récurrence un+1 = –k/(2a + un) et soit εn = |un − (b√2 − a)|. Alors on peut montrer que εn+1 < Kεn, avec 1/|1 + 2a/(b√2 − a)| < K < 1 si un est suffisamment proche de b√2 − a.
Développements en série et produit infini[modifier | modifier le code]
Produits infinis[modifier | modifier le code]
L’identité cos(π/4) = sin(π/4) = 1/√2 et la représentation en produit infini du sinus et du cosinus mènent aux développements suivants
Le dernier produit peut s’écrire de manière équivalente :
Séries[modifier | modifier le code]
Le nombre peut aussi être évalué sous forme de série en utilisant le développement de Taylor d’une fonction trigonométrique en :
On peut aussi utiliser la fonction √1 + x en 1 :
La convergence de la dernière série peut être accélérée par le biais d’une transformation d’Euler pour donner :
Développement en série de Engel[modifier | modifier le code]
Le développement en série de Engel est :
Développement en cotangente continue de Lehmer[modifier | modifier le code]
Le développement en cotangente continue de Lehmer est :
Méthodes numériques d'approximation[modifier | modifier le code]
√2 vaut approximativement 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737. Pour plus de décimales, voir la suite A002193 de l'OEIS.
Le calcul d’une valeur approchée de √2 a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d’extraction de racines carrées. En informatique, ces recherches se sont poursuivies afin d’optimiser ces algorithmes en réduisant les temps de calcul et la consommation de mémoire[56].
À l'exclusion de l'algorithme de la potence, les méthodes numériques d’approximation présentées ci-dessous sont destinées au calcul d’un nombre important de décimales. Elles se basent généralement sur une suite convergente de nombres rationnels ; ainsi l’itération s’affranchit du coût de calcul sur des nombres à virgule flottante — dont il faudrait en plus connaître la précision a priori. Les meilleures approximations par une suite rationnelle pn/qn donnent une erreur en 1/qn², une propriété de l’approximation diophantienne des entiers quadratiques.
Méthodes à convergence linéaire[modifier | modifier le code]
Algorithme de la potence[modifier | modifier le code]
Cette méthode ancienne (on la trouve en Chine dans Les Neuf Chapitres sur l'art mathématique[57] au IIIe siècle et en Inde dans l'Āryabhaṭīya[58] au Ve siècle) permet de déterminer à la main les décimales successives d'une racine carrée, mais les divisions à effectuer augmentent rapidement de taille. Ci-dessous, l'algorithme de la potence pour le calcul des 5 premières décimales de √2.
| 2 | 1,41421 | |||||||||||
| – | 1 | 1×1=1 | ||||||||||
| 1 | 0 | 0 | ||||||||||
| – | 9 | 6 | 24×4=96 | |||||||||
| 4 | 0 | 0 | ||||||||||
| – | 2 | 8 | 1 | 281×1=281 | ||||||||
| 1 | 1 | 9 | 0 | 0 | ||||||||
| – | 1 | 1 | 2 | 9 | 6 | 2824×4=11296 | ||||||
| 6 | 0 | 4 | 0 | 0 | ||||||||
| – | 5 | 6 | 5 | 6 | 4 | 28282×2=56564 | ||||||
| 3 | 8 | 3 | 6 | 0 | 0 | |||||||
| – | 2 | 8 | 2 | 8 | 4 | 1 | 282841×1=282841 | |||||
| 1 | 0 | 0 | 7 | 5 | 9 |
Méthode de Théon de Smyrne[modifier | modifier le code]
On doit à Théon de Smyrne ces deux suites (pn) et (qn) définies par récurrence :
- pn + 1 = pn + 2qn, p0 = 1 ;
- qn + 1 = pn + qn, q0 = 1.
Ces suites sont à valeur entière strictement positive, donc strictement croissantes par récurrence, et vérifient
- pn2 − 2qn2 = (−1)n(p02 − 2q02)
de sorte que pn/qn tend vers √2.
On ne sait pas si l’intention de Théon de Smyrne était de calculer une valeur approchée de √2.
Solutions de l'équation diophantienne a²− 2b² = k[modifier | modifier le code]
Les solutions entières de l’équation a² − 2b² = k sont engendrées par récurrence
- am + 1 = 3am + 4bm
- bm + 1 = 2am + 3bm
à partir des valeurs initiales (a0, b0) = (1, 1) pour k = −1 et (3, 2) pour k = 1.
Cette méthode se déduit de celle de Théon : chaque itération de la présente correspond à deux itérations de celle-là. Ainsi, an/bn tend linéairement vers √2.
Les premières solutions sont :
- k = −1 : (1, 1), (7, 5), (41, 29), (239, 169), (1393,985),
- k = 1 : (3, 2), (17, 12), (99, 70), (577, 408), (3363, 2378).
Méthode de Théon généralisée[modifier | modifier le code]
On se donne (a, b), obtenu par la méthode de Théon, qui est donc solution de l’une des deux équations diophantiennes précédentes 2b2 = a2 – k = K, avec k = ±1 et K > 1. On peut alors écrire
- √2 = (a/b)√K/(K + k)
Les suites pn et qn définies par
- pn + 1 = (2K + k)pn + 2Kqn, p0 = 1 ;
- qn + 1 = (2K + 2k)pn + (2K + k)qn, q0 = 1.
vérifient
- (K + k)pn + 12 – Kqn + 12 = (K + k)pn2 – Kqn2 =… = k,
et donc, de la même façon que ci-dessus, la suite pn/qn converge vers √K/(K + k) = (b/a)√2. De plus, si k = 1, cette suite est croissante donc approche cette valeur par défaut, et si k = –1, elle est décroissante donc approche cette valeur par excès.
On peut utiliser cette relation pour estimer l’erreur :
- εn + 1 ≃ εn (4K + 3k)−2
et c’est une majoration si k = 1. La convergence est donc linéaire : elle fait gagner un nombre à peu près constant de décimales à chaque itération.
Cette méthode correspond à une généralisation de la méthode du paragraphe précédent au radical √K/(K + k). Pour K plus grand, la suite (qn) croit plus rapidement, donc la convergence est accélérée.
Premières approximations de √2 = 17/12 √(288/289) par approximation linéaire de √(288/289). Les paramètres sont a = 17, b = 12, K = 288, k = 1. On a
εn + 1 < 7,5 × 10-7εn (avant approximation décimale des quotients).itération valeur fractionnaire décimales exactes 0 1 1 1 19 601/13 860 1,414 213 56 2 22 619 537/15 994 428 1,414 213 562 373 09 3 26 102 926 097/18 457 556 052 1,414 213 562 373 095 048 80 4 30 122 754 096 401/21 300 003 689 580 1,414 213 562 373 095 048 801 688 72
Développement en fraction continue[modifier | modifier le code]
Une autre méthode consiste à approcher b√2 − a par sa fraction continue généralisée pour (a, b) solution de l’équation diophantienne 2b2 = a2 – k, avec k = ± 1 :
- b√2 − a = [0; –k, 2a; –k, 2a; –k, 2a…] est approximé à l’aide de la suite (pn/qn) déterminée par la relation de récurrence
- pn + 1 = qn
- qn + 1 = 2aqn + kpn
L’erreur vérifie asymptotiquement
- εn + 1 < |b√2 − a|/(2a − 1) εn
Premières approximations de √2 par approximation linéaire de 169√2 − 239. Les paramètres sont b = 169, a = 239, k = 1, εn + 1 ~ 4 × 10−6 εn. itération valeur fractionnaire décimales exactes 0 1 1 1 114 243/80 782 1,414 213 562 2 54 608 393/38 613 965 1,414 213 562 373 09 3 26 102 926 097/18 457 556 052 1,414 213 562 373 095 048 80 4 12 477 253 282 759/8 822 750 406 821 1,414 213 562 373 095 048 801 688 7
Développement en série entière[modifier | modifier le code]
On se donne (a, b) solution de l’équation diophantienne 2b2 = a2 – k = K, avec k = ±1. On peut alors écrire √K/(K + k) comme somme d'une série via le développement en série entière de (1+z)-½ (ou la formule du binôme généralisée, simple variante d'exposition).
et utiliser √2 = (a/b)√K/(K + k).
Avec a = 7, b = 5 (soit K = 50, k = -1) et donc √2 = (7/5)√50/49, les premiers termes de la série sont particulièrement simples, comme l’a fait remarquer Leonhard Euler en 1755[59] :
Approximation √2 = (239/169)√57122/57121 par le développement en série entière du radical fractionnaire. Les paramètres sont b = 239, a = 169, K = 57122, k = –1. itération valeur fractionnaire décimales exactes 0 1 1 1 239/169 1,414 2 2 6 238 763 163 557/4 411 471 739 168 1,414 213 562 373 09 3 712 741 258 857 407 100/503 984 177 369 509 000 1,414 213 562 373 095 048 4 325 705 649 507 622 468 308 893/230 308 673 437 608 741 128 192 1,414 213 562 373 095 048 801 688
Dichotomie[modifier | modifier le code]
Il est possible d’approcher √2 par bissection. Cette méthode est de convergence linéaire lente : on gagne trois décimales à chaque dizaine d’itérations.
Méthode à convergence quadratique[modifier | modifier le code]
La méthode de Newton appliquée à la fonction racine carrée permet de calculer une valeur approchée de √2 de manière itérative avec une convergence quadratique, c’est-à-dire doublant le nombre de décimales à chaque itération. La récurrence a la forme
- un + 1 = un/2 + 1/un
Cet algorithme s’appelle méthode de Héron ou méthode babylonienne car il semble que ce soit celle utilisée par les Babyloniens pour trouver des valeurs approchées de racines carrées.
Si l’on s’intéresse aux fractions successives à partir d’une valeur initiale p0 et q0, la récurrence sur le numérateur et le dénominateur sont
- pn + 1 = pn² + 2qn²
- qn + 1 = 2pnqn
Premières approximations de √2 données par la méthode de Newton. itération valeur fractionnaire décimales exactes 0 1 1 1 3/2 1 2 17/12 1,41 3 577/408 1,414 21 4 665 857/470 832 1,414 213 562 37 5 886 731 088 897/627 013 566 048 1,414 213 562 373 095 048 801 68
Méthodes cubiques[modifier | modifier le code]
Méthode de Halley[modifier | modifier le code]
La méthode de Halley est un exemple de méthode cubique. Elle cherche le zéro de ƒ(x) = x² − 2 en utilisant les deux premières dérivées. La solution itérative est
- xn + 1 = xn × (xn² + 6)/(3xn² + 2)
soit en posant xn = pn/qn :
- pn + 1 = pn(pn² + 6qn²)
- qn + 1 = qn(3pn² + 2qn²)
Cette méthode est de convergence cubique : le nombre de décimales exactes triple à chaque itération.
Premières approximations de √2 données par la méthode cubique. itération valeur fractionnaire décimales exactes 0 1 1 1 7/5 1,4 2 1 393/985 1,414 213 3 10 812 186 007/7 645 370 045 1,414 213 562 373 095 048 4 — 1,414 213 562 373 095 048
801 688 724 209 698 078 569
671 875 376 948 073 176 679 7
Méthode de Householder[modifier | modifier le code]
L’itération de Householder appliquée à ƒ(x) = 1/x ² − 1/√2 donne une suite convergeant vers 1/√2 :
- xn + 1 = xn + xn/8 × (2xn² − 1)(6xn² − 7)
Méthodes d'ordre supérieur[modifier | modifier le code]
On utilise une méthode de Newton modifiée[60] pour trouver le zéro de ƒ(x) = 1/x ² − 1/2. Cela donne la suite récurrente :
- xn + 1 = xn + xn/16 × (8hn + 6hn² + 5hn³)
avec
- hn = 1 − xn²/2
Cette méthode est de convergence quartique, c’est-à-dire d’ordre 4 : le nombre de chiffres significatifs corrects quadruple (asymptotiquement) à chaque itération.
Premières approximations de √2 données par la méthode quartique. itération valeur fractionnaire décimales exactes 0 3/2 1 1 23 169/214 1,414 2 57 367 317 478 181 000 000 000 000 000 000/2105 1,414 213 562 373 09 3 — 1,414 213 562 373 09
5 048 801 688 724 209
6 980 785 696 718 753
76 948 073 176 679 740
Il existe des méthodes d’ordre supérieur[61], notamment parmi les méthodes de Householder.
Notes et références[modifier | modifier le code]
- Voir (en) Eric W. Weisstein, « Pythagoras’s Constant », sur MathWorld.
- On peut cependant remarquer que pour le format A4, et si le petit côté vaut exactement 21 cm, le grand côté (29,7 cm) ne diffère de 21 √2 cm que de 15 microns.
- (en) Matthew Cole, « A Tedious Explanation of the f/stop », .
- (en) « ƒ/Calc Manual ».
- Cette démonstration est proposée par Socrate dans Platon, Ménon 82.
- Guillaume Reuiller, L'aire de RIEN, Palais de la découverte, mesure vérifiable sur un plan de 1841.
- « Par ce moyen on fait un cloître, en donnant autant aux voies qu’au jardin » in Dominique Raynaud, « Le schème, opérateur de la conception architecturale », Arquitetura Revista, vol. 1, , p. 15-32 (lire en ligne), p. 23.
- (en) Alexander Bogomolny, « Square root of 2 is irrational », sur Cut The Knot en recense 27.
- Contrairement à ce qu’on lit souvent, il ne s’agit pas d’un véritable raisonnement par l’absurde ; se reporter à cet article pour une analyse soignée de la différence.
- Gardner 2001, p. 16. A. Bogomolny, sur Cut The Knot (Proof 8), signale également la note, dès l'édition de 1920, de (en) E. T. Whittaker et G. N. Watson, A Course of Modern Analysis, CUP, , 608 p. (ISBN 978-0-521-58807-2, lire en ligne), p. 5.
- Gardner 2001, p. 18, présente cette reformulation pour la variante 2r/s (égale à 2/√2 = √2 et dont le dénominateur s vérifie r < s < q).
- Cette démonstration, reprise de Apostol 2000, est inspirée selon lui d'une preuve géométrique de l'époque grecque classique. On la trouve sous une forme proche dans un manuel russe de géométrie dû à A. P. Kiselev dans de 1892 et très utilisé selon Alexander Bogomolny - Cut the Knot. Une variante est donnée dans Gardner 2001, p. 12.
- La démonstration par pliage, menée en partant d'un carré est proposée par J. H. Conway et R. K. Guy, The Book of Numbers, Copernicus, p. 183-184.
- (en) A. Bogomolny, « Square root of 2 is irrational », sur Cut The Knot Proof 14'.
- Christine Proust, « Mathématiques en Mésopotamie », CultureMath, éditeur=ENS Ulm/DGESCO, (lire en ligne).
- Cette conclusion est émise par Jens Høyrup. Des éléments de traduction de la tablette sont disponibles à : La pensée algébrique, 12e Colloque Inter-IREM, 1998.
- Fowler et Robson 1998.
- Benoît Rittaud, « À un mathématicien inconnu ! », sur Bibnum.
- Plofker 2009, p. 17-18.
- Plofker 2009, p. 20-21.
- Plofker 2009, p. 21.
- Plofker 2009, p. 28.
- Plofker 2009, p. 28 qui donne des références pour certaines d'entre elles note 16 de la même page. Voir aussi l'une de ces reconstructions dans le rapport sur les recherches en éducations de la fédération Wallonie-Bruxelles de 2004 « Pour une culture mathématique accessible à tous », chapitre 20 La Diagonale du carré, p.549-551.
- Caveing 1998, p. 75
- Berggren 1984
- Fowler 1999, p. 7-8, une traduction en français du XIXe siècle est accessible en ligne, voir p. 173-191.
- Fowler 1999, p. 359, une édition bilingue du XIXe siècle est accessible en ligne, voir lignes 50, 51.
- Caveing 1998, p. 133.
- Fowler 1999, p. 302 remarque qu'Aristote, alors qu'il cite souvent cet exemple de l'incommensurabilité de la diagonale au côté, ne précise jamais de quel polygone il s'agit.
- Aristote, Analytiques postérieurs, I, 23,41 a 26-32 et I, 44,50 a 36-38 cité d'après Caveing 1998, p. 132, une édition bilingue du XIXe siècle est accessible en ligne I, 23 et I, 44.
- Par exemple dans la Métaphysique, A, 2, Métaphysique, Livres A à E, trad. Bernard Sichère, Paris, Pocket, 2007, p. 35 : « [les hommes] s'étonnent [...] de ce qu'on ne peut mesurer la diagonale du carré, puisqu'il semble tout à fait merveilleux à tous ceux qui n'en ont pas encore envisagé la raison qu'une chose ne puisse pas être mesurée par la plus petite unité. » Mais cette traduction ajoute forcément des précisions à l'original, cf. la note citée précédemment, et note 18 de la traduction Pierron et Zevort, voir aussi la traduction plus littérale de Victor Cousin du même passage qui ne mentionne pas de carré.
- Caveing 1998, p. 219-223, voir aussi l'entrée fraction continue dans l'index.
- Caveing 1998, p. 245-253, section 3.2 Y a-t-il une preuve générale dans les livres Arithmétiques ?.
- Knorr 1975, p. 22 et note 15 p. 52. La proposition est rejetée en annexe de l'édition Heilberg, édition de référence des Éléments, et donc absente du livre X, dans les traductions réalisées à partir de celle-ci.
- Voir Fowler 1999, p. 294-295 et Knorr 1975 VII.3 pour le détail de l'argumentation : la démonstration d'Alexandre d'Aphrodise utilise les Éléments, pourtant bien que reposant sur le même principe, elle est différente de la proposition X, 117.
- Knorr 1975, p. 52 note 15.
- Fowler 1999, p. 294-295.
- Saito 2004, p. 189
- Saito 2004, p. 187-189 pour un historique très synthétique, voir aussi Berggren 1984, et Caveing 1998.
- Une telle reconstitution a été donnée par Oskar Becker, décrite par Caveing 1998, p. 134-135, elle s'appuie sur une représentation géométrique des nombres, en l'occurrence des quadrillages ou des points disposés en carré, arithmétique des nombres figurés attribuée aux pythagoriciens, dont il faut alors admettre qu'elle est pratiquée par des mathématiciens grecs du Ve siècle av. J.-C., pythagoriciens ou autres, cf. Caveing.
- Caveing 1998, p. 111-112.
- Knorr 1975, p. 31.
- À la différence de la figure ci-dessus, celles des historiens font apparaître explicitement les carrés, par exemple Caveing 1998, p. 124.
- Caveing 1998, p. 229.
- Caveing 1998, p. 230 et p. 157-164.
- Kurt von Fritz s'appuie pour cette hypothèse et sur des auteurs tardifs comme Jamblique et sur la figure du pentagramme, dans un article paru en 1945, The discovery of irrationality by Hippasus of Metapontum. L'article a fait date, même si ses conclusions sont depuis contestées Saito 2004, p. 189, voir pour des discussions à ce sujet Knorr 1975, p. 29-36, Caveing 1998, p. 99-119.
- Caveing 1998, p. 145.
- Pour se faire une idée des concepts que les Grecs utilisaient, voir Knorr 1975, p. 14-17 (Introduction, §III. Indispensable definitions) en particulier p. 15.
- DahanPeiffer, p. 101.
- DahanPeiffer, p. 102.
- DahanPeiffer, p. 102-103.
- DahanPeiffer, p. 103.
- le signe √ est introduit, sous une form proche, par Christoff Rudolff en 1525 : DahanPeiffer, p. 104.
- DahanPeiffer, p. 103-104.
- Dans (de) Richard Dedekind, Stetigkeit und irrationale Zahlen, (lire en ligne) p. 27, voir Fowler 1992.
- La plupart des logiciels mathématiques, sur ordinateurs ou sur machines à calculer, utilisent des approximations préétablies de cette constante, au moins jusqu’à un certain rang.[réf. nécessaire]
- Karine Chemla et Guo Shuchun, Les neuf chapitres : Le classique mathématique de la Chine ancienne et ses commentaires [détail de l’édition], p. 322-329
- W. E. Clark, Aryabatha, Aryabhatiya of Aryabhata, p. 24 et suivantes, lire en ligne
- (la) Euler, Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum, vol. II (lire en ligne), chap. 4 (« De conversione functionum in series »), p. 292.
- (en) Newton's method and high order iterations, Xavier Gourdon et Pascal Sebah, 2001.
- (en) Xavier Gourdon et Pascal Sebah, « Pythagoras’ Constant √2 », .
Bibliographie[modifier | modifier le code]
- (en) Tom M. Apostol, « Irrationality of The Square Root of Two — A Geometric Proof », The American Mathematical Monthly, vol. 107, no 9, , p. 841-842 (lire en ligne)
- A. Dahan-Dalmedico et J. Peiffer, Une histoire des mathématiques : Routes et dédales, [détail des éditions]
- (en) David Fowler, « Dedekind's theorem √2 × √3 = √6 », The American Mathematical Monthly, vol. 99, no 8, , p. 725-733 (lire en ligne)
- (en) Martin Gardner, A Gardner's Workout : Training the Mind and Entertaining the Spirit, A K Peters, , 319 p. (ISBN 978-1-56881-120-8), p. 9-19.
- Benoît Rittaud, Le Fabuleux Destin de √2, Le Pommier, , 456 p. (ISBN 2746502755)
Mathématiques en Mésopotamie[modifier | modifier le code]
- (en) David Fowler et Eleanor Robson, « Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context », Historia Mathematica, vol. 25, , p. 366-378 (lire en ligne)
Mathématiques indiennes[modifier | modifier le code]
- (en) David Henderson, « Square Roots in the Sulbasutra », dans C. A. Gorini, Geometry at Work: Papers in Applied Geometry, coll. « MAA Notes » (no 53), , p. 39-45, en ligne sur le site de l’auteur
- (en) Kim Plofker, Mathematics in India, Princeton University Press (Princeton), (ISBN 978-0-691-12067-6).
Mathématiques grecques[modifier | modifier le code]
- (en) J.L. Berggren, « History of Greek mathematics: A survey of recent research », Historia Mathematica, vol. 11, no 4, , p. 394-410 (DOI 10.1016/0315-0860(84)90024-7)
- Maurice Caveing, La figure et le nombre : Recherches sur les premières mathématiques des Grecs, Presses universitaires du Septentrion, , 424 p. (ISBN 978-2-85939-494-3, lire en ligne), p. 33-75
- Denis Daumas, « Sur la démonstration de l’irrationalité chez les grecs », in La démonstration mathématique dans l’histoire, IREM de Lyon
- (en) David Fowler, The Mathematics of Plato’s Academy : A New Reconstruction, Oxford, Clarendon Press (Oxford Science Publications), , 2e éd., 441 p. (ISBN 0-19-850258-3)
- (en) Wilbur Knorr, The Evolution of the Euclidean elements : a study of the theory of incommensurable magnitudes and its significance for early Greek geometry, Dordrecht/Boston, D. Reidel Publishing Company, , 374 p. (ISBN 90-277-0509-7, lire en ligne)
- (en) Ken Saito, « Studies on proportion theory and incommensurability (introduction) », dans Jean Christianidis (ed.), Classics in the History of Greek Mathematics, Springer, (ISBN 978-90-481-5850-8), p. 187-189.
- (en) Árpád Szabó, The Beginnings of Greek Mathematics, Springer, 1978 (ISBN 978-9027708199).
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Livre X des Éléments d’Euclide
- Duplication du cube, racine cubique de deux
- Proportion d'argent ()
- Racine douzième de deux
Liens externes[modifier | modifier le code]
- Racine de 2, Benoît Rittaud (ressources en ligne autour du livre Le Fabuleux Destin de √2)
- (en) Eric W. Weisstein, « Pythagoras’s Constant », sur MathWorld
Bibliographie[modifier | modifier le code]
Ludmila Duchêne et Agnès Leblanc, Rationnel mon Q, Hermann, (présentation en ligne) (démonstrations de l’irrationalité de racine de 2)


![{\displaystyle {\sqrt {\sqrt {2}}}={\sqrt[{4}]{2}}=2^{1/4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/774e3fbafb9712d3bdc776386938652b8ae55d35)
![{\displaystyle {\sqrt {\sqrt {\sqrt {2}}}}={\sqrt[{8}]{2}}=2^{1/8}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8e2bee42c8f36ce0c3e96b6daf47632e5388c2c)










![{\displaystyle {\sqrt {2}}=[1;2,2,2\ldots ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0dbeae9f92742759a87834443c0c2fefbc3602f)





























