Notion de module
Un module est une unité de mesure conventionnelle adoptée pour régler les diverses parties d'un ensemble (construction, machine…). Il correspond à la plus petite commune mesure que doivent posséder les dimensions des éléments entrant dans la composition de cet ensemble pour qu’ils puissent se superposer, se combiner ou se juxtaposer sans retouches. En grec, le module est désigné par τόνος, le ton ; l’origine latine[1] modulus, de modus indique la cadence, la mesure. Le terme peut également être employé dans le sens d'étalon, de gabarit ou encore de calibre. Enfin, par extension il désigne aussi un élément, une unité constitutive d'un ensemble.
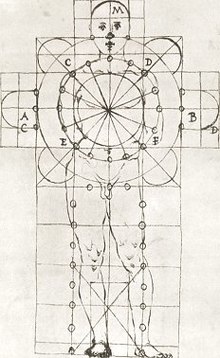
Principe[modifier | modifier le code]
Soit M le module, unité de mesure conventionnelle. À partir de M, on détermine différentes dimensions Di d’un ensemble. Pour Vitruve, le rythme modulaire comprend[2]
- les symetriae : ;
par exemple, dans l’ordre dorique, l’entablement vaut 3,5 modules, celui-ci correspondant au demi-diamètre des colonnes qui se mesure à la naissance du fût ; - les proportiones : ;
par exemple dans l’ordre dorique, « l’entablement est à la colonne comme 1 à 4 ».

Lorsque M = φ (le nombre d'or), les deux grandeurs Di et Dj sont dites dans la divine proportion.
Par la suite, il n’y a rien d’étonnant à ce qu’on appelle « module », le rapport de deux grandeurs, comme pour caractériser des propriétés physiques ou mécaniques :
- Quotient du diamètre primitif par le nombre de dents = module d’un engrenage ; tous les éléments d'un mécanisme denté — pignons, crémaillères, vis sans fin — ont le même module, ce qui assure qu'ils s'engrènent correctement ;
- Rapport entre la pression qui s’exerce sur un corps et la diminution du volume unitaire qui en résulte = module de compressibilité ;
- Débit moyen annuel (litres par seconde) par km2 = module spécifique ou relatif d’un bassin hydrographique ;
- Contrainte mécanique σ qui engendrerait un allongement ε de 100 % de la longueur initiale d'un matériau = module de Young noté E et tel que σ = E⋅ε et (loi de Hooke) qui caractérise la rigidité d’un matériau ;
- Diamètre comparatif = module des médailles ou monnaies.
Il n'y a rien d'étonnant non plus de retrouver ce terme pour désigner un élément constitutif d'un ensemble : module lunaire, module de commande, module d'une formation ou encore module d'extension d'un logiciel etc.
Le Doryphore de Polyclète[modifier | modifier le code]

En sculpture, le canon est un ensemble de règles servant à déterminer les proportions idéales du corps humain .
La théorie du canon de Polyclète est l’une des bases du classicisme grec : il l’appliqua à ses statues viriles comme le Diadumène et le Doryphore avec laquelle Polyclète avait entrepris de démontrer, par une « statue dont toutes les parties seraient entre elles dans une proportion parfaite », quels sont les rapports de grandeur dans lesquels la nature a placé la perfection des formes humaines. Il atteignit si bien son but que la statue qu'il donna comme exemple et comme modèle fut considérée comme un chef-d'œuvre incontestable. Dans cette œuvre, la tête entre au total sept fois dans le corps, deux fois entre les genoux et les pieds, deux fois dans la largeur des épaules et deux fois dans la hauteur du torse.
Les mécaniciens grecs : de l'établissement des proportions au module[modifier | modifier le code]

La genèse d’un corpus technique[modifier | modifier le code]
Si on se perd en conjectures sur l’origine de la technique, l’origine de la technologie semble correspondre à l’avènement du traité qui suppose un début de rationalisation pour transmettre un savoir-faire. À partir du VIe siècle av. J.-C. s’établit une filiation, une tradition qui permet de transmettre l’acquis technique d’une génération à l’autre. Dans ce schéma, les savoir-faire individuels sont progressivement intégrés dans un corpus qui devient accessible à tous.
La formation de l’esprit technique[modifier | modifier le code]
Dans La formation de l’esprit scientifique, Gaston Bachelard distingue trois étapes décisives qui peuvent s’appliquer peu ou prou aux techniques grecques[3] :
- L’étape primitive dans laquelle les observations ne peuvent conduire à rien, car elles butent sur des difficultés insurmontables ;
- L’étape intermédiaire dans laquelle on a su distinguer des éléments fondamentaux. C’est précisément l’étape qui permet de dégager soit un module pour la construction, soit une formule applicable.
- L’étape décisive dans laquelle le fait technique est relié à un système scientifique abstrait. La science grecque sera essentiellement axiomatique et ne permettra pas d’accéder au rêve des mécaniciens de lui donner une véritable formulation mathématique.
Les tours de Diadès[modifier | modifier le code]
Diadès fut élève de Polyeidos de Thessalie et ingénieur d’Alexandre le Grand. Il composa un traité de machines de guerre aujourd’hui perdu et se donna comme l’inventeur de tours transportables ainsi que de divers engins tels le trépan, le corbeau, le pont volant[4]. Les tours étaient de hauteur variable et constituées de plusieurs étages bordés d’un chemin de ronde, et dont la hauteur allait en diminuant. La tradition affirme qu’on prenait soin de conserver toujours les mêmes « proportions de dimension, de matériaux » dans les tours de différentes hauteurs. Après « expérience » et réflexions, on était donc arrivé à des notations chiffrées, applicables à tous les cas. Pour chaque machine on possédait des « tables de proportions » qu’il fallait suivre rigoureusement : c’est là la première utilisation connue du principe du module.
Philon d’Athènes et les proportions des temples[modifier | modifier le code]
Philon d'Athènes vivait à la fin du IVe siècle. D’après Vitruve, il aurait travaillé au temple de Cérès et de Proserpine, à Eleusis[5]. Il aurait écrit un traité de poliorcétique et un traité sur les proportions des temples aujourd’hui perdu et dont on retrouve la mention dans l’œuvre de Vitruve.
La vis d’Archimède[modifier | modifier le code]

Né et mort à Syracuse, Archimède n’appartient pas au sens strict à l’école d'Alexandrie dont il est pourtant proche tant par les problèmes étudiés que par les méthodes employées. À l’époque de l’auteur, la vis d'Archimède existait probablement depuis longtemps et l’attribution à Archimède est due à un commentaire erroné de Commandin au XVIe siècle.
Ce mécanisme nous fournit un autre exemple de l’utilisation du module par les mécaniciens grecs : dans la construction de la vis, on doit respecter des proportions qui sont énoncées sur la base d’un module qui, ici, est la longueur de la vis[6]. Le diamètre de la vis représente 1/16e de module, le pas de l'hélice 1/8e, le diamètre du cylindre enveloppe est égal au pas de l’hélice. L’inclinaison de l’ensemble doit être de 3 hauteurs pour 4 de base ce qui représente le triangle pythagoricien[7]
Philon de Byzance et les machines de jet[modifier | modifier le code]

Philon de Byzance, qui vécut à Alexandrie et à Rhodes, est le premier mécanicien dont l’œuvre nous soit en grande partie parvenue. Son traité des machines de jet montre clairement l’évolution vers l’artillerie névrobalistique. Il nous apprend que les premiers ingénieurs qui s’occupèrent de perfectionner ces machines n’agirent que par empirisme, car « les anciens avaient seulement conçu la forme et la disposition générale de ces machines, ils n’obtenaient pas de portées remarquables parce que les proportions qu’ils utilisaient n’étaient pas bien adaptées. Leurs successeurs, enlevant de-ci, ajoutant de-là, ont rendu ces instruments harmonieux et efficaces »
Ces premiers techniciens n’avaient pas ce que Philon de Byzance appelait « l’élément premier » et qui permettait de déterminer les dimensions de chacune des pièces de la machine, lui assurant ainsi les proportions les meilleures. Ainsi apparaissent des éléments fondamentaux mesurables, comptabilisables et qui représentent la base d’une conceptualisation. On assiste alors au passage de la machine exceptionnelle à la machine rationnelle, standardisée, indéfiniment reproductible et finalement banale.

Pour ce faire, Philon de Byzance établit une relation élémentaire entre l’énergie disponible, c'est-à-dire produite par les faisceaux de fibres élastiques, et le poids du boulet. Pour déterminer l’énergie, il se base sur le diamètre du trou par lequel passent les faisceaux de fibres élastiques. La racine cubique du poids en drachmes du projectile, augmentée d’un dixième, représente le diamètre du trou du bâti exprimé en doigts (unité de mesure). Une traduction algébrique (les Grecs ne maîtrisaient pas l'algèbre) donnerait avec d le diamètre du trou du bâti et le poids du projectile. Une table permettait l’utilisation du module, que Philon de Byzance appel le ton : chaque pièce représentait alors un multiple ou une fraction du module[8]. Ainsi l’euthytone (catapulte) se trouvait tracée dans un carré dont les côtés avaient 16 modules et la palintone (baliste), dans un triangle isocèle de 19 modules de base et de hauteur. Si nous ne disposons pas des tables associées à ces machines, Philon de Byzance nous livre quelques exemples :
- Pour un poids de dix mines (soit 1000 drachmes), le diamètre des lucarnes devait être de onze doigts ;
- Pour un poids d’un talent, il devait être de 21 doigts.
Il en était de même pour les pièces de la machine, le péritrète, le barillet, l’épaisseur du moyeu, l’hypothème (support), les bras, la longueur de la corde archère, qui était double de celle des bras. Le module devient ici unité de mesure et Philon de Byzance précise que « nul n’a osé s’écarter du formulaire ». Ces machines deviennent faciles à démonter, à stocker, voire à réparer, car leur mode de conception permet l’apparition des pièces détachées.
Héron d’Alexandrie ou la tradition en marche[modifier | modifier le code]
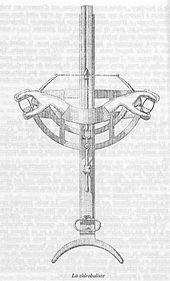
Le traité des machines de guerre d’Héron d'Alexandrie distingue deux types de machines de jet :
- Les machines euthytones qui ne lançaient que des traits (scorpions) ;
- Les machines palintones (balistes) qui lançaient des traits ou des boulets de pierre (lithoboles).
Héron d’Alexandrie reprend exactement la formule de Philon de Byzance pour le calcul du module à partir duquel toute la machine doit être construite. Il y ajoute la formule pour les machines qui lancent des traits : dans ce cas, le diamètre du trou doit être égal au neuvième de la longueur du trait. Ainsi pour un trait de 3 coudées, le module sera de 8 doigts.
Comme chez Philon de Byzance, on retrouvera dans son traité une solution graphique du célèbre problème de la duplication du cube servant ici pour calculer l’échelle de proportion de deux machines dont les boulets ont leur poids dans un rapport donné. Ainsi, pour une machine qui lancerait des boulets deux fois plus lourds, soit , on obtient aisément , ce qui correspond précisément au problème de la duplication du cube, problème qui consiste à multiplier une dimension par
Désormais, tout est défini, coté et mis en tables que personne ne peut ni ne veut modifier : cette technique est maintenant saturée.
Vitruve le compilateur[modifier | modifier le code]
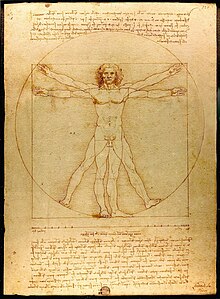
Le module a été clairement décrit par Vitruve et c'est dans ses écrits qu'apparaît pour la première fois le terme. Pourtant Vitruve ne semble être que le dépositaire d’une tradition déjà ancienne.
L’homme inscrit dans un cercle et dans un carré, réalisé sur le même dessin par Léonard de Vinci, illustre un passage du livre « De Architectura » de Vitruve (Marcus Vitruvius Pollo, Ier siècle av. J.-C., actif sous Jules César et Auguste) que la Renaissance a réédité et adulé.
Les proportions de l'homme ne concernent qu'un passage relativement court (781 mots latins) dans le chapitre 1 du livre III. Un extrait du paragraphe 2 indique clairement la mise en œuvre par l'artiste d'un « rythme modulaire » :
- « La nature a en effet ordonné le corps humain selon les normes suivantes : le visage, depuis le menton jusqu'au sommet du front et à la racine des cheveux vaut le dixième de sa hauteur, de même que la main ouverte, depuis l'articulation du poignet jusqu'à l'extrémité du majeur : la tête, depuis le menton jusqu'au sommet du crâne, vaut un huitième ; du sommet de la poitrine mesuré à la base du cou jusqu'à la racine des cheveux on compte un sixième ; du milieu de la poitrine au sommet du crâne, un quart. Quant au visage, le tiers de sa hauteur se mesure de la base du menton à la base du nez ; le nez, de la base des narines jusqu'au milieu de la ligne des sourcils, en vaut autant ; de cette limite jusqu'à la racine des cheveux on définit le front qui constitue ainsi le troisième tiers. Le pied correspond à un sixième de la hauteur du corps, l'avant-bras à un quart, ainsi que la poitrine. Les autres membres ont également des proportions spécifiques, qui les rendent commensurables entre eux…. » (…) ;
- « La proportion est le rapport que toute l'œuvre a avec ses parties, et qu'elles ont séparément, comparativement au tout, suivant la mesure d'une certaine partie. Car, de même que dans le corps humain, il y a un rapport entre le coude, le pied, la paume de la main, le doigt et les autres parties, ainsi dans les ouvrages qui ont atteint leur perfection, un membre en particulier fait juger de la grandeur de toute l'œuvre » (…) (Chapitre II : « En quoi consiste l’architecture ») ;
« L'ordonnance d'un édifice consiste dans la proportion qui doit être soigneusement observée par les architectes. Or, la proportion dépend du rapport que les Grecs appellent analogie ; et, par rapport, il faut entendre la subordination des mesures au module, dans l'ensemble de l'ouvrage, ce par quoi toutes les proportions sont réglées ; car jamais un bâtiment ne pourra être bien ordonné s'il n'a cette proportion et ce rapport, et si toutes les parties ne sont, les unes par rapport aux autres, comme le sont celles du corps d'un homme bien formé ».

Si donc la nature a tellement composé le corps de l'homme, que chaque membre a une proportion avec le tout, ce n'est pas sans raison que les anciens ont voulu dans leurs ouvrages obtenir ce même rapport des parties avec le tout.
Mais parmi tous les ouvrages dont ils ont réglé les mesures, ils se sont principalement attachés à déterminer les proportions des temples des dieux, dans lesquels ce qu'il y a de bien ou de mal fait est exposé au jugement de la postérité.
La division et même la nomenclature de toutes les mesures pour les différents ouvrages ont été prises sur les parties du corps humain ; c'est ainsi que l'on a eu le doigt, la palme, le pied, la coudée, etc., et ces divisions ont été réduites à un nombre parfait, que les Grecs appellent telion. » (Chapitre premier du livre III) ;
Ainsi dans l’architecture antique et classique, le module est la commune mesure conventionnelle d’une ordonnance correspondant en général au demi-diamètre du fût de la colonne dans sa partie basse ;
Parmi les éléments originaux notés dans l'œuvre de Vitruve, on remarque une extension remarquable de la pratique du module[9]. Pour les machines de jet, la formule des mécaniciens d'Alexandrie est adaptée aux unités de mesure romaines. Les temples sont construits à partir de modules avec la définition des ordres architecturaux (ionique, dorique). Il n'est pas jusqu'au navire où il n'est question de module et qui consiste ici en l'intervalle des chevilles sur lesquelles les rames prennent leur appui ;
Illustration des ordres architecturaux dans l'encyclopédie de Diderot et d'Alembert. Noter la référence au module comme échelle de mesure.
-
Bases des cinq Ordres avec celle nommée Attiques
-
Chapiteaux des cinq Ordres avec le Chapiteau Ionique Moderne
-
Entablements des cinq Ordres avec une Corniche Architravée
La table de Frontin[modifier | modifier le code]

Frontin appartenait à la classe sénatoriale romaine et comme tel faisait partie des personnages appelés par leur carrière à des postes militaires ou à l’administration civile[10]. En 97, on lui confie l’administration du service des eaux de Rome ; il rédigea un traité des aqueducs de Rome. Tout ce qui intéressait la jauge et le calibrage des conduites concernait au premier chef l’administration : « tout calibre est déterminé par son diamètre, ou par son périmètre ou par la mesure de sa section ». La table de Frontin est construite à partir de la quineria, tuyau de 5, jusqu’au tuyau de 125 qui permettait une classification des calibres : on parle alors de module quinaire.
Par la suite, Frontin constatera que le modèle n’est pas nécessairement homothétique, c'est-à-dire la réduction à la même échelle de tous les éléments de l’ensemble. Ainsi pour le module des tuyaux d’adduction d’eau, l’échelle des modules quant au diamètre des tuyaux fonctionne par progression arithmétique du 5 au 20. Au-dessus, il procède comme la série des racines carrées des termes d’une progression arithmétique. Des siècles plus tard, James Watt l’observera encore dans le modèle réduit de la machine de Thomas Newcomen.
Module et calligraphie arabe : de la formule d’atelier aux jeux de l’esprit[modifier | modifier le code]

Les véritables successeurs des mécaniciens grecs furent certainement les arabes qui firent traduire les traités grecs avant de s'en servir comme base pour leurs propres travaux. Par ailleurs, il semble naturel que toute civilisation[11] développe un « système esthétique » fondé sur l’amour de l’harmonie et qui peut revêtir une grande diversité de formes.

L’un des grands principes de l’esthétique, déjà énoncé par Platon, est celui de « l’harmonie des parties et du tout par laquelle l’unité de ce dernier s’impose à la multiplicité des parties ». Contrairement aux arts du monde occidental, héritiers de Platon et d’Aristote, l’art du monde musulman ne montre guère d’intérêt pour l’étude des proportions du corps humain. Si, dans le Coran, « Dieu a créé l’homme harmonieusement » (XXXII, 9), la préoccupation des artistes musulmans ne sera précisément pas de rivaliser avec cette divine justesse. En revanche, un champ de l’art tout à fait spécifique au monde musulman est fourni par la calligraphie arabe[12]. Celle-ci est d’abord développée pour la copie du Coran et les usages de la chancellerie califale et sera codifiée en une « écriture proportionnée » (al-khatt al-mansûb) attribuée au vizir Ibn Muqla (885/886-940). Dans son « traité sur l’écriture et le calame » (Risâlat al-khatt wa-l-qalam), l’auteur donne les bases d’un système de proportions fondé sur la lettre alif, en forme de hampe verticale et qui est inscrite dans un cercle servant d' étalon (module). Chaque lettre est ensuite formée à partir de ce cercle ce qui donnera les six styles de la calligraphie arabe classique (naskhî, Muhaqqaq, thuluth, riqa’, rayhânî et tawqî), chacun se caractérisant par la proportion des lettres par rapport au alif.
Cette conception très intellectualisée de la calligraphie sera reprise ensuite par toutes les grandes écoles de calligraphie. Dès le début du XIVe siècle, chez les Mamelouks d’Égypte ou chez les Mongols d’Iran, on observe dans la production de manuscrits de prestige un développement du souci de mise en page. Ainsi le format des feuillets de papier présente souvent des proportions remarquables : les plus fréquentes sont A (1 × 1,414)[13], le double rectangle de Pythagore (1 × 1,5) et plus rarement, le rectangle d’or (1 × 1,618).
De plus, le champ de la page est divisé entre le rectangle calligraphique, ou espace écrit, et la marge, tous deux répondant à des rapports précis. La surface écrite est divisée par la réglure, la largeur de la page divisée par un nombre entier donne alors le nombre de lignes. Plus tard avec Villard de Honnecourt, ou comme l'a montré Rosa Viro avec la bible de Gutenberg [14], les typographes suivront des tracés régulateurs ou des modes de calcul pour déterminer l'empagement d'un ouvrage, afin d’assurer une répartition cohérente des blancs et de la surface imprimée[15]
Module, figures de référence et tracé régulateur[modifier | modifier le code]

De nombreuses constructions à la règle et au compas conduisent à la mise en œuvre de figures géométriques types, telles que le pentagone, figures elles-mêmes associées à des modules particuliers (nombre d'or dans le cas de pentagone).
En architecture il est possible de construire des volumes selon toutes sortes de proportions. L'architecture classique donnait trois « moyennes proportionnelles » pour trouver la hauteur d'une pièce à partir de sa base :
- la moyenne arithmétique : ;
- la moyenne géométrique : ;
- la moyenne harmonique : .
Dans les théories de la Renaissance, la base a des proportions comprises entre 1 et 2 en passant par 7 positions intermédiaires : 1/1, 4/5, 3/4, 1/√2, 3/2, 1/Φ, 3/5, 4/7 et 1/2. Ces proportions découlent directement de Pythagore et de Platon.
Pourtant ces calculs ne sont souvent que théoriques. Ainsi Andrea Palladio a publié la description des bâtiments qu'il a construits dans son traité d'architecture I quattro libri dell'architettura (Les Quatre Livres de l'architecture). Dans ce traité, il explique qu'il a utilisé ces méthodes pour dimensionner les pièces et il cote ses dessins.
« Les proportions des voix sont harmonie pour les oreilles, celles des mesures sont harmonie pour les yeux. De telles harmonies plaisent souvent beaucoup sans que quiconque sache pourquoi, à l'exception des chercheurs de la causalité des choses[17]. »
Cependant une mesure précise des bâtiments montre qu'il peut y avoir des écarts assez importants entre la théorie et la réalité[18]. Le plan de la villa Rotonda est construit selon le système de la moyenne géométrique.
Plus près de nous, un architecte Le Corbusier, qui a travaillé sur la notion de « tracé régulateur », s'est inventé un système de mesures basé sur la suite de Fibonacci : le Modulor. Si on prend un exemple, les maisons Jaoul, dont les façades sont composées selon le Modulor, on se rend compte qu'en réalité les mesures toutes théoriques sont difficiles à retrouver dans le bâtiment. Il n'en reste pas moins que cette mise en théorie de l'arrangement non des pièces à vivre mais des équipements du second-œuvre mis dans ces volumes obtenus a donné la pratique utilisée dans toute l'architecture « modulaire »[19] européenne du XXe siècle « le module de 30/60 cm » et dimensionné toutes les baies et portes standards.
Le module vu par les encyclopédistes des Lumières[modifier | modifier le code]
L'Encyclopédie de Diderot et d'Alembert consacre un article au module. Les trois acceptions principales sont celles relatives aux médailles et monnaies, à l'architecture et aux mathématiques avec le module d'un logarithme :
« MODULE » : s. m. (Alg. & Géom.) Quelques auteurs appellent ainsi la ligne qu’on prend pour sous-tangente de la logarithmique dans le calcul des logarithmes. Voyez. Ainsi, dans les logarithmes de Neper, le modale est 0, 434294 ; et, dans les logarithmes de Briggs, c’est l’unité. Quand on dit qu’une ligne est le logarithme du rapport de a à b, c étant pris pour module, cela veut dire que cette ligne est l’abscisse d’une logarithmique dont la sous-tangence est c, cette abscisse étant comprise entre deux ordonnées égales à a et à b. M. Côtes, dans son Harmonia mensurarum (commentée & développée par dom Walmesley dans son Anasyse des rapports), emploie fréquemment cette expression de module qui d’ailleurs n’est que fort peu usitée. (O).
(sc), (Art numism.) terme emprunté de l’Architecture par les Médaillistes, pour fixer par des grandeurs déterminées leurs médailles, & en composer les différentes suites dans les médailliers ; ils ont réduit, ainsi, toutes les grandeurs des médailles de bronze à trois modules, qu’ils nomment des pièces de grand, de moyen et de petit bronze, & on écrit par abréviation G. B. M. B. P. B. (D. J.).
(sc), (Architedure.) mesure prise à volonté pour régler les proportions des colonnes et la symétrie ou la distribution de l’édifice.
Les architectes prennent d’ordinaire pour module le diamètre, mais le plus souvent le demi-diamètre du bas de la colonne et ils le subdivisent en parties ou minutes.
Vignole partage son module, qui est le demi-diamètre de la colonne, en douze parties égalées pour les ordres toscan et dorique, en dix-huit pour les autres ordres. Palladio. Scamozi, Desgodetz et Le Clerc, divisent leur demi-diamètre en trente parties ou minutes dans tous les ordres. Quelques-uns partagent toute la colonne en seize parties pour la dorique, en dix-huit pour l’ionique, en vingt pour la corinthienne et d’une de ces parties ils font un module pour régler le reste de l’édifice.
Il y a deux manières de déterminer les mesures et les proportions des bâtiments. La première, par une mesure fixe ou une espèce de talon qui sont ordinairement le diamètre de la partie inférieure de la colonne, lequel s’appelle module et est divisé en soixante parties nommées minutes. Il est une autre manière de déterminer les mesures et les proportions des ordres, dans laquelle il n’entre ni minute, ni division certaine, mais on divise leur hauteur suivant l’occasion en autant de parties qu’on juge à propos ; c’est ainsi que la base attique se divise ou en trois pour avoir la hauteur de la plinthe, ou en quatre pour avoir celle du plus grand tort, ou en six pour en constater celle du plus petit, &c.

Module et machine à vapeur, dans l’attente d’une théorie générale[modifier | modifier le code]

Les premières machines à vapeur d’application pratique étaient apparues au début du XVIIIe siècle et fonctionnaient à pression atmosphérique. Afin de supprimer le gaspillage de chaleur lié au réchauffement et au refroidissement alternatif d’un unique cylindre (machine de Newcomen), James Watt condensa la vapeur dans un cylindre froid séparé appelé condenseur. Arthur Woolf introduisit dès le début du XIXe siècle le moteur compound à haute pression fonctionnant par expansion, dans lequel la vapeur agit d’abord à haute pression dans le petit cylindre (B) puis par expansion dans le grand cylindre (A). En l’absence d’une théorie générale, les ingénieurs cherchèrent à déterminer le « rapport de volume » dans lequel ils devaient placer les deux cylindres : environ 1 à 4,5 soit un taux de détente de 9 pour la machine de Woolf[20], 1 à 8 soit un taux de détente de 64 pour la machine de Jacob Perkins. Pour Sadi Carnot, « Les machines à deux cylindres, quoique conçues sur d’assez bons principes, se trouvent souvent loin de produire les résultats avantageux que l’on aurait droit d’attendre d’elles. Cela tient surtout à ce que les dimensions des diverses parties de ces machines sont difficiles à bien régler, et qu’elles se trouvent rarement dans un juste rapport les unes avec les autres » [21].
À l’instar d'Émile Clapeyron (X 1816), de Gabriel Lamé (X 1814) ou encore d’Antoine Raucourt (X 1809), le jeune officier Sébastien de Maillard séjourna plusieurs années à Saint-Pétersbourg où le français était alors la langue véhiculaire de l’aristocratie et de l’intelligentsia. Ses écrits attestent des tentatives pour contourner les obstacles scientifiques à l’aide de modules dans l’étude de la machine à vapeur où l'emploi des proportions permet de ne pas expliciter des constantes souvent difficiles à déterminer.
Un peu plus tard, dans les Réflexions, Sadi Carnot « maintient le calcul à son rang de moyen et se contente volontiers d’être un virtuose de la proportionnalité – un style très ancien ». Dans cet ouvrage il posa le théorème du rendement maximum qui le conduisit à « substituer la différence des chaleurs spécifiques à pression et à volume constants à leur rapport, comme constante spécifique » [22] soit
Avec la machine à vapeur, pivot de la révolution industrielle, l’utilisation de module sous forme de rapports de grandeurs caractéristiques fut une fois encore une étape importante pour concilier réalisation pratique et recherche d’une théorie générale. L'industrie généralisa par la suite une façon différente de créer des gammes de tailles : les séries de Renard.
Le module, des réalisations pratiques aux sources de la théorie[modifier | modifier le code]

Dans le domaine de la technique, le module a donné un début de rationalisation qui a ouvert la voie au triomphe de la technologie.
En architecture, l’utilisation du module permet de respecter des proportions et ainsi de s’affranchir de calculs précis sur la résistance des matériaux, calculs aujourd’hui indispensables pour assurer la solidité des édifices (par exemple pour éviter le flambage d'une poutre en compression). En ce sens, le module a sans doute permis d’obtenir des solutions approchées, mais satisfaisantes pour résoudre des problèmes concrets de dimensionnement.
Le module permet d’aider à définir diverses dimensions utiles au technicien dans sa recherche d’une solution adaptée. Il constitue en ce sens une recette largement répandue comme le montrent les études sur les équerres médiévales qui mettent en œuvre quelques angles caractéristiques comme 36° pour le Triangle d’or, 30 et 60 ° voir plus rarement 54 ou 26 °.
En caractérisant les propriétés mécaniques de certains matériaux (module de rigidité, de traction, de torsion...), le module permet ensuite d’utiliser des formules algébriques pour résoudre des problèmes concrets. Ainsi le module de Young, qui caractérise la rigidité des matériaux, sera intégré dans « l’équation d’équarrissage » qui servira à dimensionner les poutres des abattoirs grâce aux calculs de déformation des poutres en flexion.
La tradition persistera jusqu’à la machine à vapeur, pour laquelle Sébastien de Maillard et ses prédécesseurs tenteront de contourner les obstacles scientifiques à l’aide de modules. Dans ce cas l'emploi des proportions permet de ne pas expliciter des constantes souvent difficiles à déterminer. De la même façon, dans ses expériences sur la chute des graves, Galilée ignorait que le roulement de la boule sur le plan incliné « absorbait » les 2/7e de g : en procédant par comparaison avec un jet de référence (un module) il s'affranchissait de la connaissance de cette donnée inaccessible à l’époque [23]. Si l’accélération du mouvement est connue depuis Aristote, Galilée ne se demande plus pourquoi la vitesse augmente, mais bien comment elle augmente et surtout dans quelles proportions [24] ce qui constituera une étape fondamentale pour se libérer des spéculations[25].
Module dans l'industrie[modifier | modifier le code]
Le général français Jean-Baptiste de Gribeauval, dès 1765, a développé la notion d'interchangeabilité pour pouvoir échanger rapidement des pièces défectueuses de mousquets et de pistolets avec des pièces de remplacement récupérées sur d’autres pistolets sur le champ de bataille même.
En 1877, on a confié au colonel Renard la tâche d'améliorer les ballons captifs. Il s'est alors aperçu que l'armée utilisait 425 tailles de câbles pour amarrer les ballons. Il a cherché à diminuer leur nombre à 17 tailles en proposant de les classer suivant une suite géométrique où la masse augmente d'un facteur 10 au cinquième pas.
- avec :
- d'où : = 1,58489319
Avec a = 10, on obtient la série de Renard R5 : 10, 16, 25, 40, 63, 100, ...
Pour normaliser les dimensions des pièces dans l'industrie, l'ISO a adopté les séries de Renard R5, R10, R20, R40 et exceptionnellement R80 comme séries de nombres préférés dans la norme ISO 3 - 1973 pour le système métrique SI.
D'autres séries de nombres dimensionnels préférés ont été adoptés dans certaines branches industrielles :
- pour les monnaies on utilise la série 1-2-5 ;
- dans l'électronique, la série E a été adoptée comme norme internationale CEI 60063 pour les résistances, les condensateurs, les inductances et les diodes Zener ;
- dans les formats de papiers, on a adopté une série en racine carrée, (√√√2, √√2, √2, 2, ou 2√2) de la norme ISO 216
- en informatique, on se sert de séries de nombres en puissance de 2 : 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, ...
D'autres systèmes de modules de nombres préférés existent dans d'autres branches industrielles.
Module en mathématique[modifier | modifier le code]
Le terme de module est aussi employé en mathématiques (échelle logarithmique, module d'un nombre complexe, arithmétique modulaire, module sur un anneau, forme modulaire) avec plusieurs sens différents.
Pour une échelle logarithmique, le module est l'unité de longueur qui sépare le logarithme de 0,1 et celui de 1, égale à la distance entre le logarithme de 1 et celui de 10 ou de 10 et de 100. Le sens de « mesure » est aussi à l'origine de la signification du terme pour les nombres complexes. Jean-Robert Argand utilise ce vocable[26] pour désigner la norme, c'est-à-dire la longueur au sens géométrique du vecteur qui représente ce nombre.
L'origine sémantique en arithmétique est différente. Carl Friedrich Gauss parle[27] de « module » pour désigner la « cadence » de l'anneau Z/nZ. Les termes de période de Gauss et d'analyse harmonique sont toujours utilisés dans ce domaine mathématique. Ce mathématicien écrit en latin.
Les autres définitions, plus tardives, proviennent d'une généralisation du sens donné par Gauss et ne font plus référence à la langue morte. Elle tombe en désuétude comme langue scientifique. Les anneaux d'entiers possèdent parfois un groupe des unités analogue à Z/nZ, comme pour l'ensemble des entiers de Gauss. Le cas général est un peu plus complexe, la structure est élucidée par le théorème des unités de Dirichlet. Elle correspond à un groupe abélien de type fini. Par extension du vocabulaire défini par Gauss, on parle alors de module sur un anneau. L'utilisation de ce terme dépasse maintenant le cadre de l'arithmétique. Le terme de forme modulaire est un autre avatar de l'arithmétique. Il désigne une fonction analytique définie par un groupe de congruences, encore analogue à la construction de Gauss, et qui porte le nom de « groupe modulaire ».
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Bertrand Gille :
- (s. dir.), Histoire des techniques, Gallimard, coll. « La Pléiade », 1978 (ISBN 978-2070108817) ;
- Les Ingénieurs de la Renaissance, Thèse Histoire, Paris, 1960 ; Seuil, coll. « Points Sciences » 1978 (ISBN 2-02-004913-9) ;
- Les mécaniciens grecs, Seuil / science ouverte, 1980 (ISBN 2-02-005395-0) ;
- L'Âge d'or des sciences arabes, Actes Sud / Institut du monde arabe, oct. 2005 (ISBN 2-7427-5672-8) ;
- La Recherche en histoire des sciences, Le Seuil / La Recherche, 1983 (ISBN 2-02-006595-9) ;
- Collectif, Sadi Carnot et l'essor de la thermodynamique, CNRS Éditions (1er septembre 1998) (ISBN 2-222-01818-8) ;
- Le Nouveau Petit Robert de la langue française 2007. (ISBN 2-84902-260-8) .
- Gaston Bachelard, La formation de l'esprit scientifique, Bibliothèque des textes philosophiques, VRIN (ISBN 2-7116-1150-7) ;
- La révolution mathématique du XVIIe siècle - Évelyne Barbin – Éditions Ellipses (ISBN 2729831444).
Notes et références[modifier | modifier le code]
- Datée de 1547 - Le nouveau Petit Robert de la langue française 2007
- (s. dir.) Bertrand Gille : Histoire des techniques
- Les mécaniciens grecs p. 219
- Les mécaniciens grecs p. 42
- Les mécaniciens grecs, p. 49
- Les mécaniciens grecs, p. 155
- Le triangle pythagoricien est le triangle rectangle par excellence : côtés de l'angle droit de 3 unités et 4 unités, hypoténuse 5 unités. Ce triangle a donné lieu à la création de la corde à 13 nœuds (12 intervalles) qui permet de le reconstituer facilement, car 3 + 4 + 5 = 12
- Les mécaniciens grecs p. 113
- Les mécaniciens grecs p. 155
- Les mécaniciens grecs p. 160
- Au Japon la dimension du tatami, appelé alors jō (畳, じょう), constitue une unité de mesure pour les pièces de la maison : encore aujourd'hui, on parle couramment d'une pièce de 8 tatamis, comprenez une pièce qui peut accueillir 8 tatamis. De ce fait, la largeur du tatami devient le module de référence dans la construction de l'habitat traditionnel : les pièces, mais aussi les portes, les fenêtres et les volets sont dimensionnés dans cette unité.
- L'Âge d'or des sciences arabes, Actes Sud / Institut du monde arabe p. 251
- Le rapport de la longueur à la largeur de la feuille de base vaut . Ce rapport (module) est remarquable au sens où il a la propriété de se conserver lorsqu'on plie ou coupe la feuille en deux dans sa grande dimension. Voir aussi Racine carrée de deux
- « Typographie de la bible de Gutemberg »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)
- En savoir plus
- Ce type de plan se retrouve également pour l'Église ronde de Véliki Preslav
- Les quatre livres de l'architecture - Éditions Arthaud Paris 1980 - Préface de François Herbert Stevens
- Rudolf Wittkower, Les principes de l'architecture à la Renaissance, éditions de la Passion, Traduction française de 1996 (ISBN 2-906229-30-X)
- CNRTL, [ définition module], (ARCHIT. MOD. et CONTEMP.) Unité de base dont les mesures du bâtiment sont des multiples; élément simple d'une structure répétitive. « La diversité des procédés et des modules architecturaux, la souplesse d'urbanisation, sont indispensables dans une civilisation que sa finalité traditionnelle place au service de la personne humaine. Gds ensembles habit., 1963, p.7. »
- Sadi Carnot et l'essor de la thermodynamique, CNRS Éditions. p. 139
- Sadi Carnot et l'essor de la thermodynamique, CNRS Éditions. p. 147. Cette citation fait étrangement écho à celle de Philon de Byzance relative aux machines de jet et rédigée vingt-deux siècles plus tôt
- Sadi Carnot et l'essor de la thermodynamique, CNRS Éditions. p. 123
- Galilée et l'expérimentation - La Recherche en histoire des sciences p. 134
- La révolution mathématique du XVIIe siècle - Évelyne Barbin. Voir aussi Mathématiques en Europe au XVIIe siècle
- Voir Mathématiques en Europe au XVIIe siècle.
- Jean-Robert Argand Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques 1806 Gauthier-Villars, Paris 1874
- Carl Friedrich Gauss, Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Éd. Courcier page 1 1807
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- « Module » dans l'Encyclopédie ou dictionnaire raisonné des sciences, des arts et métiers ;
- Architecture (planches) dans l'Encyclopédie ou dictionnaire raisonné des sciences, des arts et métier, Volume 1 ;
- La codification du plan des villes ;
- Méthodes d'empagement - Les tracés régulateurs.
 |
Cet article contient des extraits de l'Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, publiée au XVIIIe siècle dont le contenu se trouve dans le domaine public. |




![{\displaystyle d=1,1{\sqrt[{3}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d534ee4cdf8ebc52c87a5d0af6e2a3eed96566)


![{\displaystyle d'=d{\sqrt[{3}]{2}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/734c801052e4cceec3a4e73d214d537d516c10d3)
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)




![{\displaystyle h={\sqrt[{}]{l*L}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f5b767db92d5d5752679a7973d47f49ead6411)




![{\displaystyle q={\sqrt[{5}]{10}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10f651788d55ad1cc70e54c7fa2b7f4909ffcaf5)
