Similitude (géométrie)
En géométrie euclidienne, une similitude est une transformation qui multiplie toutes les distances par une constante fixe, appelée son rapport. L'image de toute figure par une telle application est une figure semblable, c'est-à-dire intuitivement « de même forme ».

Les isométries, c'est-à-dire les transformations qui conservent les distances sont des cas particuliers de similitudes ; elles transforment des figures en des figures de même forme et de même taille. Les autres similitudes sont les composées d'une isométrie et d'une homothétie qui agrandit ou réduit la taille des figures. Parmi les similitudes, certaines conservent l'orientation, elles sont appelées similitudes directes. Les autres sont appelées similitudes indirectes.
Dans le plan, les translations, les rotations, les symétries orthogonales selon un axe, les homothéties sont des cas particuliers de similitudes. On démontre qu'une similitude plane est toujours décomposable en au plus deux transformations de ce type. L'expression complexe d'une similitude plane est la donnée de la relation entre l'affixe d'un point et l'affixe de son image, l'expression complexe d'une similitude directe est celle d'une application affine sur le corps des complexes .
Dans un espace euclidien quelconque, la similitude se décrit à l'aide d'une matrice. Dans le cas d'une similitude vectorielle, cette matrice est inversible et la matrice inverse est proportionnelle à la matrice transposée.
Une similitude peut aussi se définir plus généralement dans un espace vectoriel quelconque muni d'une forme quadratique.
Similitudes planes[modifier | modifier le code]
Définitions[modifier | modifier le code]
Définitions équivalentes[modifier | modifier le code]

Si l'on considère, dans le plan euclidien, une transformation, c'est-à-dire une bijection du plan dans lui-même, ƒ, les propositions suivantes sont équivalentes :
- ƒ multiplie les distances par un réel strictement positif k ;
- ƒ conserve les rapports de distances ;
- ƒ conserve les angles géométriques (c'est-à-dire les mesures d'angles non orientés).
Une transformation du plan qui vérifie ces propositions est appelée une similitude du plan.
On trouve cette définition, dans de nombreux ouvrages, et dans les directives de l'Éducation nationale française[1], mais il n'est pas toujours nécessaire de supposer au départ que la fonction ƒ du plan dans lui-même soit une bijection :
- une application qui multiplie les distances par un réel strictement positif est toujours une similitude[2] ;
- une injection qui conserve les rapports de distance ou les angles orientés ou seulement l'orthogonalité est une similitude[3].
Les similitudes conservant les rapports de distances et les alignements, conservent également les barycentres et les cercles. Réciproquement, une transformation du plan qui transforme des cercles en des cercles est une similitude[4].
Similitudes directes et indirectes[modifier | modifier le code]
Les similitudes qui conservent les angles orientés sont appelées des similitudes directes, les autres similitudes sont appelées indirectes. On démontre que les similitudes indirectes planes changent tous les angles orientés en leur opposé.
Les isométries directes sont appelés des déplacements. Les isométries indirectes sont appelées des antidéplacements.
Éléments caractéristiques[modifier | modifier le code]
Rapport d'une similitude[modifier | modifier le code]
Le rapport d’une similitude est le coefficient k de proportionnalité entre les longueurs d’une première figure géométrique, et les longueurs correspondantes dans l’image de la première par la similitude. Pour le déterminer, il suffit de connaitre deux points distincts A et B et leurs images, A' et B'. Le rapport de la similitude est alors le rapport .
Autrement dit, dans une similitude de rapport k, la seconde figure reproduit la première à l’échelle k. Le nombre k × k ou k2 est alors le coefficient de proportionnalité entre les aires correspondantes. Par exemple, une similitude de rapport dix multiplie les longueurs par dix et les aires par cent.
Si le rapport est plus grand que 1, les figures sont agrandies, si le rapport est plus petit que 1, les figures sont réduites. Si le rapport est égal à 1, les figures gardent la même taille, la similitude est alors une isométrie.
Les homothéties sont des similitudes, et il faut noter l’ambiguïté du mot rapport à leur sujet. Le rapport d’une homothétie concerne des vecteurs, il peut être négatif, tandis que le rapport d’une similitude est un rapport de distances, toujours positif. Par exemple, une homothétie de rapport négatif –1 est une similitude de rapport positif 1, on peut la voir comme une symétrie par rapport à son centre ou une rotation d’angle 180° (un demi-tour). Dans tous les cas, une homothétie de rapport k est une similitude de rapport positif |k|.
Le propre des similitudes est d'envoyer toute figure sur une figure semblable, c'est-à-dire « de même forme » mais pas nécessairement « de même taille ». Par exemple : * l'image d’un carré par une similitude est un carré ;
- tout triangle rectangle isocèle est semblable à n’importe quel triangle rectangle isocèle ;
- n’importe quel cercle est semblable à n’importe quel cercle.
Une similitude transforme un triangle équilatéral en un triangle équilatéral.
Angle d'une similitude directe[modifier | modifier le code]
Une similitude directe conserve les angles orientés. On démontre alors que l'angle que forme un vecteur avec son image est constant. Cet angle est appelé l'angle de la similitude directe.
Dans le cas d'une similitude indirecte, l'angle que forme un vecteur avec son image est variable. C'est la raison pour laquelle on ne peut pas définir d'angle pour une similitude indirecte plane.
Similitudes à centre[modifier | modifier le code]
Toute similitude de rapport k différent de 1, c'est-à-dire toute similitude différente d'une isométrie, possède un unique point invariant I qui est appelé le centre de la similitude. Il existe plusieurs méthodes pour déterminer géométriquement le centre d'une similitude connaissant deux points distincts A et B et leurs images A’ et B’.

L'une d'entre elles consiste à utiliser le fait que l'ensemble des points M vérifiant est un cercle de diamètre A1A2 où A1 et A2 sont les barycentres de A et A’ affectés des coefficients k et ±1. Le centre I de la similitude est situé sur les cercles et . En général, ces cercles se rencontrent en deux points. L'un est le centre de la similitude directe transformant (A, B) en (A’, B’), l'autre est le centre de la similitude indirecte.
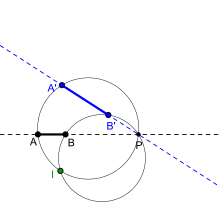
Pour la recherche du centre de la similitude directe transformant (A, B) en (A’, B’), Euler[5] propose une méthode plus simple utilisant les cercles circonscrits.
- Le cas où les segments [AB] et [A’B’] sont parallèles est rapidement traité : ƒ est alors une homothétie et son centre est le point d'intersection des droites (AA’) et (BB’). Les cas particulier où A = A’ ou B = B’ ne sont pas étudiés car le centre de la similitude est immédiat. Le cas où les 4 points seraient alignés nécessite la construction à l'aide de triangles directement semblables de points C et C’ non alignés avec A et B.
- Quand les droites (AB) et (A’B’) sont sécantes en P, il suffit de construire les cercles circonscrits aux triangles AA’P[6] et BB’P. Le centre de la similitude est l’autre point commun aux deux cercles[7]. Cette méthode utilise le fait que I et P regardent les points A et A’ et les points B et B’ sous le même angle égal à l'angle de la similitude directe. Les points IPAA’ d'une part et IPBB’ d'autre part, sont donc, selon la propriété des angles inscrits, cocycliques.
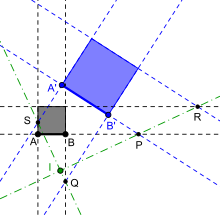
Mais il existe une méthode pour trouver le centre d'une similitude directe ne demandant pas la construction de cercles[8]. Elle utilise le fait que, dans un similitude directe de centre I, les droites (MM’) et (NN’) sont parallèles si et seulement si les points I, M et N sont alignés ainsi que les points I, M’ et N’. Il suffit alors de construire deux carrés ABCD et A’B’C’D’ directement semblables. Comme dans la méthode précédente, le cas où les droites (AB) et (A’B’) sont parallèles est facile à traiter. Dans le cas contraire, on construit les points d'intersections P, Q, R et S des droites (AB) et (A’B’), (BC) et (B’C’), (CD) et (C’D’), (DA) et (D’A’). Le point d'intersection des droites (PR) et (QS) fournit le centre de la similitude. Le principe est que P et son image sont sur (A’B’), R et son image sont sur (C’D’). Les droites (PP’) et (RR’) sont parallèles, le centre de la similitude est alors sur (PR) et (P’R’).
Les isométries, quant à elles, sont de 4 types :
- celles qui ne possèdent aucun point invariant (translation de vecteur non nul pour les déplacements, ou symétrie glissée pour les antidéplacements) ;
- celles qui possèdent un seul point invariant I (les rotations de centre I d'angle non nul) ;
- celles qui possèdent une droite comme ensemble de points invariants (les réflexions d'axe d) ;
- celle dont tous les points sont invariants (l'application identité).
On peut utiliser l'une ou l'autre des méthodes décrites ci-dessus pour déterminer le centre d'une rotation, ou bien chercher un point commun aux médiatrices de [AA’] et [BB’] .
Inventaire et décomposition canonique[modifier | modifier le code]

Outre l'identité (similitude directe de rapport 1, d'angle nul, sans centre unique), les similitudes fondamentales sont :
- les translations de vecteur non nul (similitudes directes, de rapport 1, d'angle nul, sans centre) ;
- les rotations d'angle non nul (similitudes directes, de rapport 1, d'angle égal à celui de la rotation, de centre égal au centre de la rotation) ;
- les homothéties de rapport différent de 1(similitudes directes, de rapport égal à la valeur absolue du rapport de l'homothétie, d'angle nul si le rapport de l'homothétie est positif, d'angle plat si le rapport de l'homothétie est négatif, de centre le centre de l'homothétie) ;
- les réflexions d'axe d (similitudes indirectes, de rapport 1, sans centre).
Toute similitude est une similitude fondamentale ou la composée de deux d'entre elles. À condition de bien les choisir, ces deux similitudes fondamentales commutent entre elles, c'est-à-dire que ƒ ∘ g = g ∘ ƒ.
Inventaire des isométries[modifier | modifier le code]
- Déplacements ou isométries directes : outre l'identité, les isométries directes sont les translations et les rotations.
- Antidéplacements ou isométries indirectes : les isométries indirectes sont les réflexions, ou les symétries glissées (composée commutative d'une translation de vecteur et d'une réflexion selon un axe dont la direction est .
Inventaire des similitudes de rapport différent de 1[modifier | modifier le code]
Une similitude de rapport k différent de 1 possède un centre I. Elle est la composée commutative d'une homothétie de centre I et de rapport k et d'une isométrie à point(s) fixe(s), c'est-à-dire une rotation de centre I ou une réflexion.
- Similitudes directes : Une similitude directe de centre I, de rapport k et d'angle θ est la composée commutative d'une homothétie de centre I et de rapport k et d'une rotation de centre I et d'angle θ.
- Similitudes indirectes : une similitude indirecte de centre I et de rapport k est la composée commutative d'une homothétie de centre I et de rapport k et d'une réflexion d'axe (d) passant par I.
Caractérisation par l'image de deux points[modifier | modifier le code]
Une similitude directe ou indirecte est entièrement déterminée par l'image de deux points distincts. Plus exactement, si on considère 4 points A, B, A’, B’ tels que A ≠ B et A’ ≠ B’, il existe une unique similitude directe et une unique similitude indirecte transformant (A, B) en (A’, B’).
Similitude directe définie par l'image de deux points[modifier | modifier le code]
Le rapport k de la similitude est donné par , l'angle par . Si le rapport est 1 et l'angle est nul, il s'agit d'une translation de vecteur . Dans tous les autres cas, la similitude possède un centre I que l'on peut déterminer géométriquement.
Similitude indirecte définie par l'image de deux points[modifier | modifier le code]
Le rapport k de la similitude est donné par . On ne parle pas d'angle pour cette similitude car elle est indirecte.
- Si le rapport est 1, il s'agit d'une symétrie ou d'une symétrie glissée. En construisant le triangle A’B’A’’ indirectement semblable au triangle ABA’, on peut construire le point A1 milieu de [AA’’].
- Si le vecteur est nul, la similitude est une réflexion d'axe (d). Si A et B sont invariants, cet axe est la droite (AB), sinon cet axe est la médiatrice de [AA’] ou de [BB’].
- Si le vecteur est non nul, la similitude est alors la composée commutative de la translation de vecteur et d'une réflexion d'axe (d) passant par le milieu de [A’A1] et de direction .
- Si ce rapport est différent de 1, le centre I de la similitude peut se construire géométriquement. La similitude est alors la composée commutative d'une homothétie de centre I et de rapport k et d'une réflexion d'axe (d). Cet axe peut se construire comme la bissectrice de l'angle AIA’ ou de l'angle BIB’.
Expression complexe[modifier | modifier le code]
Dans le plan complexe, chaque point M a une affixe. Si ƒ est une application du plan dans lui-même et si on note z’ l'affixe du point M’ image du point M par ƒ, la relation existant entre z’ et z est appelée l'expression complexe de l'application.
Expression complexe d'une similitude directe[modifier | modifier le code]
Théorème — Une transformation du plan est une similitude directe si et seulement si son écriture complexe est de la forme z’ = az + b, avec fixés.
L'expression complexe permet de déterminer facilement les éléments caractéristiques d'une similitude directe :
- son rapport est égal au module de a ;
- son angle est égal à un argument de a ;
- son centre existe si et seulement si a est différent de 1, et son affixe est .
Cas spéciaux :
- Dans le cas où a = 1, la similitude est une translation.
- Dans le cas où a = –1, la similitude est une symétrie centrale de centre . On peut aussi la considérer comme une rotation de centre et d'angle π, ou encore une homothétie de centre et de rapport k = –1.
- Dans le cas où , alors la similitude est une homothétie de centre et de rapport a.
Si l'on connait deux points distincts A(zA) et B(zB) et leurs images A’(zA’) et B’(zB’), on peut déterminer les valeurs de a et b :
Expression complexe d'une similitude indirecte[modifier | modifier le code]
Une application ƒ du plan dans lui-même est une similitude indirecte si et seulement s'il existe deux complexes a et b, a étant non nul, tels que l'expression complexe de ƒ soit
- z’ = az + b.
Comme pour la similitude directe, l'expression complexe d'une similitude indirecte permet d'en déterminer les éléments caractéristiques :
- son rapport est égal au module de a ;
- une similitude indirecte n'ayant pas d'angle, on ne peut rien tirer de l'argument de a.
Selon le rapport de la similitude, les éléments caractéristiques vont changer :
- si le rapport est 1, il s'agit d'une symétrie ou d'une symétrie glissée :
- si ab + b = 0, c'est une réflexion d'axe passant par B(b/2) et de direction (ou si le vecteur précédent est nul) ;
- si ab + b ≠ 0, c'est une symétrie glissée de vecteur et d'axe passant par et de direction (ou si le vecteur précédent est nul) ;
- si le rapport est différent de 1, il s'agit de la composée d'une homothétie de rapport |a|, de centre I d'affixe avec une réflexion d'axe passant par I et de direction (ou si le vecteur précédent est nul)
Si l'on connait deux points distincts A(zA) et B(zB) et leurs images A’(zA’) et B’(zB’), on peut déterminer les valeurs de a et b :
Composition, groupes et sous-groupes[modifier | modifier le code]
Quand on compose deux similitudes de rapports k et k’ on obtient encore une similitude de rapport kk’. La réciproque d'une similitude de rapport k est une similitude de rapport 1/k. L'ensemble des similitudes muni de la composition de fonctions est donc un groupe. Celui-ci est non commutatif : la composée de ƒ par g est, en général, différente de la composée de g par ƒ.
Quand on compose deux isométries, on obtient une isométrie, et la réciproque d'une isométrie est encore une isométrie. L'ensemble des isométries est donc un sous-groupe du groupe des similitudes.
Quand on compose deux similitudes directes de rapports k et k’ et d'angles θ et θ’, on obtient une similitude directe de rapport kk’ et d'angle θ + θ’. La réciproque d'une similitude directe de rapport k et d'angle θ est une similitude directe de rapport 1/k et d'angle –θ. L'ensemble des similitudes directes est donc un sous-groupe du groupe des similitudes. Mais quand on compose deux similitudes indirectes, on obtient une similitude directe, l'ensemble des similitudes indirectes n'est donc pas stable pour la composition des fonctions.
Il existe de nombreux sous-groupes du groupe des similitudes, on peut citer par exemple, le groupe des déplacements, le groupe des homothéties- translations, le groupe des similitudes de même centre. Le sous-groupe des homothéties de centre I et le sous-groupe des translations sont des sous-groupes commutatifs.
Matrice d'une similitude vectorielle plane et lien avec l'ensemble des complexes[modifier | modifier le code]
Une similitude vectorielle plane est une application linéaire du plan vectoriel P dans lui-même qui multiplie les normes par une constante strictement positive k. Si le plan vectoriel est muni d'une base orthonormée, la similitude vectorielle est caractérisée par sa matrice.
Une matrice M est la matrice d'une similitude directe si et seulement s'il existe deux réels a et b non tous deux nuls, tels que . L'ensemble des matrices de ce type pour a et b quelconques (pouvant à présent être nuls simultanément), muni de l'addition et de la multiplication des matrices, forme un corps commutatif isomorphe au corps des complexes. Cette identité de structure a conduit à définir parfois l'ensemble des complexes comme l'ensemble de ces matrices carrées[9].
Par exemple, si a = 1 et b = 1, on obtient la similitude décrite par l'équation z’= (1 + i)z, équivalente à x’ = x – y et y’ = x + y, qui laisse stable l'anneau des entiers de Gauss.
Une matrice M est la matrice d'une similitude indirecte si et seulement s'il existe deux réels a et b non tous deux nuls tels que .
Similitude dans un espace euclidien[modifier | modifier le code]
La notion de similitude ne se limite pas à la similitude plane mais se rencontre aussi dans tout espace euclidien, c'est-à-dire tout espace vectoriel ou affine de dimension finie sur le corps des réels , muni d'un produit scalaire (u|v).
Similitude vectorielle[modifier | modifier le code]
Si φ est une application linéaire de l'espace vectoriel euclidien E dans lui-même, les propositions suivantes sont équivalentes[10] :
- il existe un réel strictement positif α tel que, pour tous vecteurs u et v, (φ(u)|φ(v)) = α(u|v) ;
- il existe un réel strictement positif β tel que, pour tout vecteur u, ∥φ(u)∥ = β∥u∥ ;
- φ possède un endomorphisme adjoint φ* et il existe un réel strictement positif γ tel que φ∘φ* = φ*∘φ = γIdE ;
- φ est non nul et conserve l'orthogonalité (les vecteurs images de deux vecteurs orthogonaux sont orthogonaux).
Un tel endomorphisme est alors appelé une similitude vectorielle. Son rapport est .
Une base orthonormée étant choisie, à chaque endomorphisme d'un espace euclidien de dimension n, on peut associer une matrice carrée M. La matrice M est la matrice d'une similitude si et seulement si[11] elle est inversible et s'il existe un réel strictement positif γ tel que tM = γM–1.
L'ensemble des similitudes vectorielles sur E muni de la loi de composition est un sous-groupe de GL(E) noté GO(E). Il est relié au groupe orthogonal O(E) par la relation suivante : l'application de ℝ*+ × O(E) dans GO(E) qui au couple (k, φ) associe l'endomorphisme kφ est un isomorphisme de groupes. Le groupe des similitudes vectorielles est produit direct du sous-groupe des isométries et du sous-groupe des homothéties de rapport strictement positif.
Comme il existe des isométries directes formant le groupe O+ (E) et des isométries indirectes réunies dans l'ensemble O– (E), on peut définir les similitudes directes formant le groupe GO+ (E) et des similitudes indirectes réunies dans l'ensemble GO– (E). Si la similitude est directe, le déterminant de sa matrice est positif. Sinon il est négatif.
Similitude affine[modifier | modifier le code]
Une application affine ƒ d'un espace affine dans lui-même dont l'application linéaire associée est une similitude vectorielle est appelée une similitude affine[2]. Pour un espace affine euclidien, le sous-groupe des similitudes affines est le produit semi-direct des translations par le groupe des similitudes vectorielles.
Une application de dans lui-même est une similitude directe de rapport k strictement positif si et seulement si elle multiplie les distances par k[2].
Une bijection ƒ de dans lui-même est une similitude si et seulement si elle vérifie l'une des propriétés suivantes[12] :
- ƒ conserve l'orthogonalité ;
- ƒ transforme les sphères en sphères ;
- ƒ conserve les angles géométriques.
Si k est égal à 1, la similitude affine est une isométrie affine. Si k est différent de 1, la similitude affine possède une unique point invariant I appelé centre de la similitude, elle est la composée commutative d'une homothétie de centre I et de rapport k avec une isométrie dont l'ensemble des points invariants contient au moins le point I[2].
Dans l'espace affine de dimension 3 par exemple, les similitudes affines sont
- si k = 1, les isométries de l'espace (symétrie centrale, rotation suivant un axe, symétrie orthogonale par rapport à un plan, composée d'une rotation d'axe (d) avec une symétrie orthogonale de direction (d), translation, vissage, symétrie glissée) ;
- si k est différent de 1, la similitude est une homothétie de rapport k ou la composée commutative d'une homothétie de centre I et d'une rotation suivant un axe contenant I ou la composée commutative d'une homothétie de centre I et d'une symétrie orthogonale par rapport à un plan contenant I ou la composée commutative d'une homothétie de centre I et d'une rotation suivant un axe contenant I et d'une symétrie orthogonale par rapport à un plan passant par I et orthogonal à (d). De telles transformations multiplient les longueurs par k, les aires par k² et les volumes par k3.
Afin de représenter toutes ces transformations par des multiplications matricielles de même format, le graphisme numérique utilise toujours les coordonnées homogènes. De longueur n + 1, la dernière ligne d’une telle matrice est alors toujours la même, inutile de la ranger en mémoire pour chaque transformation. Son dernier terme 1 est précédé de termes tous nuls.[réf. souhaitée]
Les similitudes : un des outils de construction des systèmes de fonctions itérées[modifier | modifier le code]
Beaucoup d'attracteurs classiques de systèmes de fonctions itérées sont construits avec des similitudes. Souvent même, même si pas toujours, les éléments d'une famille de contractions seront des similitudes[13].
Similitude à multiplicateur et forme quadratique[modifier | modifier le code]
La notion de similitude peut se généraliser à tout espace quadratique (espace vectoriel V sur un corps K muni d'une forme quadratique Q).
Un automorphisme φ est une similitude de multiplicateur α non nul si et seulement si[11] pour tout vecteur v de V, Q(ƒ(v)) = αQ(v). Une homothétie de rapport k non nul est un exemple de similitude de multiplicateur k².
Si Q est non dégénérée, un automorphisme φ est une similitude de multiplicateur α si et seulement si[11] il possède un endomorphisme adjoint φ* vérifiant φ* = αφ-1.
Si le corps K est le corps des réels, et si Q est définie positive, c'est-à-dire si elle est associée à un produit scalaire, le réel α est strictement positif et sa racine carrée est le rapport de la similitude.
Notes et références[modifier | modifier le code]
- Programme TS 2002, Document d'accompagnement, p. 60.
- Tauvel 2005, p. 113.
- Tauvel 2005, p. 114.
- Tauvel 2005, p. 115.
- Euler2012, p. 1;2
- Si P est confondu avec A (ou A’), on trace le cercle passant par A’ et A et tangent à la droite (AB) (ou à (A’B’)
- Si les deux cercles sont tangents, on considère que les deux points d'intersections sont confondus et I = P
- Programme TS 2002, Document d'accompagnement, p. 64-65
- Voir par exemple M. Queysanne et A. Revuz, Mathématiques, Terminales C et E, t. 1, Nathan, ou bien l'arrêté du 14 mai 1971 B.O.E.N. 25 (24-6-71).
- Tauvel 2005, p. 112
- Chambadal 1969, p. 205
- Tauvel 2005, p. 114;115
- (en) « Fractals and Self-Similarity », Indiana University of Mathematics Journal, (lire en ligne)
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Direction de l'enseignement scolaire, ministère de l'éducation nationale, Mathématiques : Classes terminales de la série scientifique, Paris, Centre national de documentation pédagogique, coll. « Lycée / Accompagnement des programmes », , 123 p. (ISBN 2-240-00854-7)
- Patrice Tauvel, Géométrie : agrégation, licence 3e année, master, Paris, Dunod, , 532 p. (ISBN 2-10-049413-9)
- Lucien Chambadal, Dictionnaire des mathématiques modernes, Larousse,
- Homer S. White, « Leonard Euler on the Center of Similitude »









































![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)



