Entier quadratique
En mathématiques, un entier quadratique est un nombre complexe, racine d'un polynôme unitaire du second degré à coefficients entiers. La notion de nombre algébrique de degré inférieur ou égal à 2 est plus générale : elle correspond à un nombre complexe, racine d'un polynôme du second degré à coefficients seulement rationnels.
Ces nombres particuliers disposent de propriétés algébriques. Si α est un entier quadratique, l'ensemble ℤ[α] des nombres de la forme a + bα, où a et b désignent deux entiers relatifs, est un sous-anneau du corps ℂ des nombres complexes (c'est-à-dire qu'il est stable par addition, soustraction et multiplication et qu'il contient 1). Si β est un nombre algébrique de degré 2, l'ensemble des nombres de la forme a + bβ, où a et b désignent deux rationnels, est toujours un anneau unitaire et même un corps (tout élément non nul est inversible), appelé corps quadratique et noté ℚ(β).
Un nombre quadratique, entier ou seulement algébrique, est ainsi avant tout un élément d'un ensemble, structuré par deux opérations. Cette approche est au cœur de la théorie algébrique des nombres. Au lieu d'étudier un nombre particulier, comme le nombre d'or, l'analyse de la structure d'anneau associé, ici celui des entiers du corps ℚ(√5) est plus fructueuse. Cette démarche est ancienne, dès le VIe siècle les mathématiciens indiens avaient déjà découvert une multiplication sur un ensemble de cette nature, qui permet de résoudre certains cas particuliers de l'équation de Pell-Fermat. Au XIXe siècle, Gauss préfigure la démarche moderne et fixe le vocabulaire avec l'étude des entiers portant maintenant son nom. Il découvre que cet anneau est euclidien, permettant de développer une arithmétique analogue à celle des entiers relatifs, avec sa version du théorème fondamental de l'arithmétique et ses nombres premiers.
Ces structures sont parfois sujettes à des difficultés, qualifiées d'obstructions. L'une concerne les éléments inversibles qui sont parfois en nombre infini. Une deuxième obstruction existe si l'anneau n'est par exemple pas euclidien ni même principal. L'unicité de la décomposition en « facteurs premiers » ne s'applique plus et les techniques usuelles de l'arithmétique s'avèrent inopérantes. Une analyse plus profonde de la structure de l'anneau permet d'y remédier à l'aide du concept d'idéal d'un anneau.
Les anneaux d'entiers quadratiques forment en général la première classe d'exemples dans laquelle on tente de faire fonctionner des théories inaccessibles dans le cas général (voir par exemple le théorème de Kronecker-Weber en théorie des corps de classes). L'étude des entiers quadratiques admet une version plus algébrique : l'étude des formes quadratiques binaires et de leur réduction de Gauss, qui reflète les propriétés arithmétiques des corps quadratiques (groupe des classes d'idéaux en particulier). Il n'y a pas[réf. nécessaire] d'analogue à cette interprétation dans les corps de nombres en général.
Préambule[modifier | modifier le code]
Le nombre d désigne dans le reste de l'article un entier sans facteur carré et différent de 1, la lettre ℤ désigne l'anneau des entiers relatifs, ℚ le corps des rationnels et ℂ celui des complexes.
Motivation[modifier | modifier le code]
La première motivation historique est la résolution d'équations diophantiennes du deuxième degré. Ces équations sont à coefficients entiers et les solutions recherchées sont entières. Un exemple célèbre est x2 – 61y2 = 1, traité[1] par Brahmagupta, un mathématicien indien, et repris par Fermat dans un défi présenté à la communauté européenne en 1657[2].
En vue de résoudre cette équation, il est judicieux d'étudier les nombres de la forme a + b√61, ici a et b désignent deux entiers relatifs. On remarque que si α et β sont de cette forme, alors leur somme et leur produit le sont aussi. De plus, si α et β correspondent à deux couples d'entiers solutions de l'équation, alors c'est aussi le cas pour αβ. Résoudre l'équation revient en fait à déterminer un sous-ensemble particulier de l'anneau unitaire des entiers quadratiques de la forme a + b√61. Cet ensemble correspond à un sous-groupe du groupe des unités, le groupe multiplicatif des éléments possédant un inverse dans l'anneau (si a2 – 61 b2 = 1, l'inverse de a + b√61 est a – b√61).
Un deuxième exemple est l'étude des propriétés arithmétiques associées au nombre d'or φ = (1 + √5)/2. Une fois encore, les nombres de la forme a + bφ forment une structure stable pour l'addition et la multiplication, appelée anneau. Elle est particulière dans le sens où elle admet une division euclidienne. Cette division euclidienne offre une structure suffisamment proche de celle des entiers relatifs pour que le terme d'entier soit utilisé pour écrire un élément de l'ensemble. Les techniques de résolution sont absolument analogues à celle de l'arithmétique élémentaire.
En ajoutant des éléments à ℤ de façon à obtenir un corps, on construit ℚ, son corps des fractions. Lorsqu'on applique la même technique à un anneau d'entiers quadratiques, on obtient un corps quadratique. Cette structure est la « première marche » d'une tour d'extensions quadratiques, l'un des fondements de la compréhension des figures constructibles à la règle et au compas.
Anneaux euclidiens[modifier | modifier le code]
Les entiers algébriques d'un corps quadratique ℚ(√d) forment un anneau aux propriétés variables en fonction de la valeur de d. Son groupe des unités est connu pour chaque valeur de d. Il est fini si d < 0.
Cet anneau est euclidien pour la norme définie ci-dessous (ou sa valeur absolue, si d > 0) si et seulement si d est l'une des 21 valeurs suivantes :
Si d = –1, l'anneau est celui des entiers de Gauss. Il est formé des nombres complexes de la forme a + ib avec a et b deux entiers relatifs et i l'unité imaginaire.
Si d = –3, l'anneau est celui des entiers d'Eisenstein.
Lorsque l'anneau est euclidien, il est principal donc factoriel.
Groupe des unités[modifier | modifier le code]
Si d est positif (par exemple si d = 5), une première difficulté apparait : le groupe des unités de l'anneau des entiers de ℚ(√d) (c'est-à-dire l'ensemble des éléments inversibles muni de la multiplication) est infini. Pour la résolution d'équations diophantiennes comme celle du « dernier théorème de Fermat » pour les « petits » exposants, ne serait-ce que pour n = 5, les contournements deviennent acrobatiques. Dirichlet appelle « obstruction » cette difficulté.
Anneaux non factoriels[modifier | modifier le code]
Lorsque l'anneau est principal, les outils de l'arithmétique élémentaire s'appliquent avec succès. Le lemme d'Euclide, l'identité de Bézout ou encore la décomposition en facteurs premiers se traduisent pratiquement sans modification, hormis l'identification ci-dessus du groupe des unités. Ceux plus sophistiqués de l'arithmétique modulaire comme le passage au quotient, le petit théorème de Fermat ou la loi de réciprocité quadratique se généralisent aussi.
Le théorème de Stark-Heegner précise pour quels entiers négatifs d l'anneau est principal :
L'anneau des entiers de ℚ(√d), pour d entier négatif sans facteur carré, est principal si, et seulement si, d est l'une des neuf valeurs suivantes :
−1, −2, −3, −7, −11, −19, −43, −67 et −163.
Dans le cas des entiers d positifs, les anneaux principaux sont beaucoup plus nombreux, mais la conjecture de Gauss selon laquelle il existerait une infinité de corps quadratiques réels dont l'anneau des entiers est principal n'est toujours pas résolue.
Lorsque l'anneau est principal, il est factoriel. Ces deux notions sont en fait équivalentes pour l'anneau des entiers d'un corps quadratique ou plus généralement d'un corps de nombres, car il est de Dedekind.
Mais lorsqu'il ne l'est pas, les deux caractérisations usuelles dans ℤ[3] des nombres premiers ne sont plus équivalentes car un élément (non nul et non inversible) irréductible, c'est-à-dire ne possédant pas d'autre diviseur que 1 et lui-même (à produit près par les inversibles) n'est plus nécessairement premier au sens du lemme d'Euclide, si bien qu'un élément peut avoir plusieurs décompositions différentes en produit d'irréductibles. Par exemple dans l'anneau ℤ[i√5] des entiers de ℚ(i√5),
De même, ℤ[i√3], sous-anneau de l'anneau euclidien des entiers d'Eisenstein, n'est pas factoriel car
(on peut aussi, pour celui-ci, arguer du fait qu'il n'est pas intégralement clos : cf. § Fermeture intégrale et clôture intégrale).
Caractérisation[modifier | modifier le code]
Nombre algébrique de degré 2[modifier | modifier le code]
L'étude des entiers quadratiques fait intervenir les nombres plus généraux répondant à la définition suivante :
- Un nombre algébrique est dit de degré 2 si son polynôme minimal est de degré 2.
Le polynôme minimal d'un nombre algébrique α est le polynôme unitaire à coefficients rationnels de plus petit degré dont α est racine. Ainsi, un nombre complexe est algébrique de degré 2 si et seulement s'il est non rationnel et solution d'une équation du second degré à coefficients rationnels.
L'intérêt de cette notion provient de structures algébriques sous-jacentes à un tel nombre. On étudie plus les propriétés des structures associées que le nombre lui-même.
- Si α est un nombre algébrique de degré 2, le plus petit sous-corps de ℂ contenant α est l'ensemble ℚ(α) des nombres complexes de la forme x + yα.
Un tel corps est une extension quadratique de ℚ, or (cf. section suivante) une telle extension est toujours de la forme ℚ(√d) pour un certain entier sans facteur carré d ≠ 1. Il existe une convention prise ici, que les analystes ne font pas. Il n'est dit nulle part que d est un entier positif, ce qui sous-entend que l'expression √d peut décrire la racine carrée d'un nombre négatif. En analyse, cette situation est dangereuse, on ne sait pas si cette racine désigne i√–d ou –i√–d et il n'est pas possible d'adopter une convention qui rende la fonction racine continue sur l'ensemble des nombres complexes. Le paragraphe suivant montre que cette difficulté n'existe pas dans le contexte de cet article. Pour une raison de commodité, l'usage du radical racine pour des entiers négatifs est fréquent en théorie algébrique des nombres[4], cette convention est utilisée ici.
Si α est algébrique de degré 2, ℚ(α) est égal à un certain ℚ(√d) et α appartient à ℚ(√d). Réciproquement, un élément a + b√d de ℚ(√d) est solution de l'équation X2 – 2aX + (a2 – db2) = 0 donc est soit algébrique de degré 1 c'est-à-dire rationnel (si b = 0), soit algébrique de degré 2. On en déduit la caractérisation suivante des nombres algébriques de degré 2 :
- Un nombre α est algébrique de degré 2 si, et seulement s'il existe deux rationnels b non nul et a, et un entier sans facteur carré d ≠ 1, tels que α est égal à a + b√d.
Corps quadratique[modifier | modifier le code]
Le corps ℚ(√d) est isomorphe à l'anneau quotient ℚ[X]/(X2 – d) et toutes les extensions quadratiques de ℚ sont de cette forme (cf. article détaillé), ce qui justifie la définition suivante :
- Un corps quadratique est un sous-corps de ℂ de la forme ℚ(√d), où d est un entier sans facteur carré différent de 1.
Ainsi, tout nombre algébrique α de degré 2 appartient à un unique corps quadratique ℚ(α) = ℚ(√d) et tous les éléments d'un corps quadratique sont algébriques de degré 1 ou 2. C'est même une propriété caractéristique des corps quadratiques :
- Tout corps commutatif contenant strictement ℚ et qui ne contient que des nombres algébriques de degré 1 ou 2 est isomorphe à un corps quadratique.
(Une démonstration est proposée dans l'article détaillé.)
Entier quadratique[modifier | modifier le code]
Un entier algébrique est un nombre algébrique dont le polynôme minimal (donc pris unitaire) est à coefficients dans ℤ. Un nombre α est algébrique de degré 1 si et seulement si c'est un rationnel ; son polynôme minimal est alors X – α. Les seuls entiers algébriques de ℚ sont donc les éléments de ℤ. Comme dans tout autre corps algébrique[5] on peut, dans un corps quadratique, s'intéresser aux éléments qui sont entiers algébriques :
Un entier quadratique est[6],[7] un entier algébrique qui est de degré 1 ou 2 en tant que nombre algébrique.
Tout entier quadratique est donc élément d'un corps quadratique.
L'article détaillé montre que (de même que ℤ dans ℚ) l'anneau OK des entiers d'un corps algébrique K, constitué des entiers algébriques de K, mérite son nom d'anneau, en tant que fermeture intégrale[8] dans K d'un sous-anneau : ℤ. En particulier pour un corps quadratique :
La somme, la différence et le produit de deux entiers algébriques d'un corps quadratique est un entier algébrique.
On peut le vérifier directement en caractérisant d'abord l'anneau des entiers d'un corps quadratique :
L'anneau des entiers de ℚ(√d) est ℤ[(1 + √d) / 2] si d est congru à 1 modulo 4, et ℤ[√d] sinon[9].
L'expression « ℤ[ω] » désigne l'ensemble des nombres de la forme a0 + a1ω + a2ω2 + … + anωn, où a0, a1, … , an sont des éléments de ℤ. Ici, ω2 s'écrit toujours comme une combinaison linéaire à coefficients dans ℤ de 1 et de ω, elle est donnée par le polynôme minimal, si ω désigne une des valeurs de l'énoncé de la proposition, à savoir (1 + √d) / 2 ou bien √d. Dans toute la suite de l'article ω désigne cette valeur. Un élément de l'anneau ℤ[ω] est donc de la forme a + bω, où a et b sont des éléments de ℤ.
Fermeture intégrale et clôture intégrale[modifier | modifier le code]
Comme précédemment pour les corps et les nombres algébriques, on peut se poser la question de la forme d'un anneau unitaire composé uniquement d'entiers quadratiques. Hormis bien sûr ℤ, chacun d'eux est inclus dans un unique corps quadratique : son corps des fractions (c'est-à-dire, à isomorphisme près, le plus petit sous-corps de ℂ qui contient cet anneau). Cet anneau est donc inclus dans l'anneau des entiers de ce corps, ce qui permet de déterminer toutes les possibilités :
- Soit A un anneau contenant strictement ℤ et formé uniquement d'entiers quadratiques. Le corps des fractions de A est l'unique corps quadratique contenant A, et il existe un entier f, non carré parfait, tel que : ou bien A = ℤ[√f], ou bien f est congru à 1 modulo 4 et A = ℤ[(1 + √f)/2].
En particulier :
- Tout corps quadratique est le corps des fractions de l'anneau de ses entiers (de même que ℚ est le corps des fractions de ℤ).
- L'entier sans facteur carré d tel que ℚ(√d) soit le corps des fractions de A se déduit de l'entier non carré f ci-dessus : il a même signe que f et sa valeur absolue est le radical de |f|.
Par exemple :- l'anneau des entiers de ℚ(√–2) est ℤ[√–2], dont ℤ[√–18] est un sous-anneau, et leur corps des fractions commun est ℚ(√–2) ;
- l'anneau des entiers de ℚ(√–3) est l'anneau ℤ[(1 + √–3)/2] des entiers d'Eisenstein, dont ℤ[√–3] et ℤ[(1 + √–27)/2] sont des sous-anneaux, et leur corps des fractions est ℚ(√–3).
Un anneau d'entiers quadratiques – ou plus généralement d'entiers algébriques – est intégralement clos si et seulement s'il est égal à l'anneau des entiers de son corps des fractions. En effet, dans le cas général, un anneau intègre A est dit intégralement clos si sa clôture intégrale est réduite à A, cette clôture intégrale étant définie comme la fermeture intégrale de A dans son corps des fractions K (c'est-à-dire l'anneau intermédiaire des éléments de K qui sont entiers sur A) ; mais si A est constitué d'entiers algébriques, sa fermeture intégrale dans K est réduite à l'anneau des entiers de K (cf. corollaire 2 de l'article « Élément entier »). Par conséquent :
- L'anneau des entiers d'un corps quadratique est, comme ℤ, intégralement clos, et aucun anneau intermédiaire ne l'est.
Ainsi, l'anneau des entiers d'un corps quadratique n'est pas toujours factoriel, mais vérifie toujours la propriété (plus faible) d'être intégralement clos.
Outils et théorèmes[modifier | modifier le code]
Conjugué et norme[modifier | modifier le code]
Deux applications ont un rôle privilégié dans les corps quadratiques.
- L'automorphisme σ du corps ℚ(√d) qui envoie √d sur –√d.
(Si d < 0, σ est la restriction à ℚ(√d) de la conjugaison des nombres complexes.) Les deux seuls endomorphismes de ℚ(√d) sont d'ailleurs σ et l'application identité. Par restriction, on obtient :
L'involution σ est un automorphisme de l'anneau ℤ[ω] des entiers de ℚ(√d).
En effet, tout automorphisme d'un corps laisse stable l'anneau de ses entiers. Cet endomorphisme σ de ℤ[ω] est d'ailleurs le seul à part l'identité, puisqu'un tel endomorphisme est nécessairement injectif (il envoie tout élément non nul de l'anneau sur un élément conjugué donc également non nul) donc s'étend en un endomorphisme du corps des fractions ℚ(√d).
- L'application norme relative N, de ℚ(√d) dans ℚ, qui à élément α associe le déterminant du ℚ-endomorphisme x ↦ αx de ℚ(√d). On démontre que N(α) = ασ(α), donc N(a + b√d) = a2 – db2.
Par construction, cette application respecte la multiplication :Dans le cas où d est négatif, on trouve le carré de la norme géométrique usuelle. Contrairement à cette dernière, la norme arithmétique est à valeurs rationnelles. Cette propriété est essentielle pour de nombreux usages.
Si d est positif, la norme n'a pas de raison d'être positive. Par exemple N(1 + 1√2) = –1.
Dans la ℤ-base (1, ω) de Oℚ(√d) = ℤ[ω], selon que d est congru à 1 modulo 4 ou pas, donc selon que ω est égal à (1 + √d)/2 ou à √d, la norme prend la forme suivante (pour tous entiers relatifs a et b) :
Sur l'anneau ℤ[ω], la norme est donc à valeurs dans ℤ. Par multiplicativité, on en déduit que dans cet anneau[11] :
- les unités sont les éléments de norme ±1 ;
- tout élément non nul est un produit d'irréductibles[12] ;
- tout élément dont la norme est égale, au signe près, à un nombre premier, est irréductible ;
- pour tout élément π premier dans ℤ[ω] (c'est-à-dire non nul, non inversible, et vérifiant le lemme d'Euclide), il existe un entier naturel premier (au sens usuel) qui est soit associé à π, soit égal à |N(π)|.
Groupe des unités de l'anneau des entiers[modifier | modifier le code]
La première difficulté à résoudre pour comprendre la structure d'un anneau d'entiers quadratiques est son groupe des unités. Une première remarque simplifie l'analyse : un entier quadratique est inversible si et seulement si sa norme est égale à ±1, ce qui ramène la question à l'étude d'une des deux équations diophantiennes : x2 – dy2 = ±1 ou, si d est congru à 1 modulo 4 et si g désigne l'entier (d – 1)/4 : x2 + xy – gy2 = ±1.
La première équation est étudiée[14] depuis Diophante et porte le nom d'équation de Pell-Fermat. Elle est résolue de manière algorithmique par Bhāskara II[15], un mathématicien indien du XIIe siècle, et par Joseph-Louis Lagrange en 1767 de manière théorique[16], à l'aide des fractions continues d'un irrationnel quadratique.
Si d est négatif, le groupe est toujours cyclique, et même d'ordre 2 (réduit au groupe {1, –1}), sauf dans les deux cas d = –1 (ordre 4, cf. l'article « Entier de Gauss ») et d = –3 (ordre 6). Si d est positif, le groupe est infini car isomorphe à ℤ/2ℤ × ℤ. Il existe une unique unité ρ dont les deux coordonnées sont positives et telle que toute unité soit égale à ρk ou –ρk pour un certain entier relatif k. Il existe deux algorithmes célèbres et relativement efficaces pour trouver cette unité dite fondamentale.
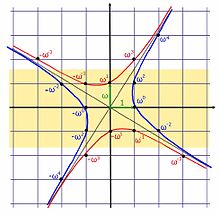
Graphiquement si l'on représente l'anneau dans le repère (1, ω) que l'on considère comme orthonormal, les points de l'anneau se situent sur le quadrillage régulier contenant le point 0 et formé de carrés de côté 1. Les éléments du groupe des unités se trouvent sur 4 branches d'hyperboles qui s'obtiennent par rotations successives d'un quart de tour.
L'analyse du groupe des unités ne nécessite pas que l'anneau soit intégralement clos. En conséquence, les résultats sont encore vrais pour un anneau d'entiers quadratiques quelconque.
Décomposition en idéaux premiers[modifier | modifier le code]
La deuxième obstruction est la conséquence de la non-principalité de certains anneaux d'entiers quadratiques, ce qui implique leur non-factorialité qui, comme on l'a vu, induit des décompositions multiples d'un entier quadratique en facteurs irréductibles. Deux théorèmes permettent encore de travailler malgré cette obstruction, ils ne s'appliquent que sur des anneaux intégralement clos, c'est-à-dire que l'anneau doit contenir tous les entiers algébriques d'un corps quadratique.
La manière d'analyser cette situation pour Ernst Kummer est de considérer qu'il « manque » des « nombres premiers ». Les idéaux premiers sont alors vus comme les nombres premiers manquants. L'objectif consiste à ne plus décomposer un nombre mais un idéal car on a la propriété remarquable suivante de « factorialité en idéaux » :
Dans l'anneau OK = ℤ[ω] des entiers d'un corps quadratique K, tout idéal non nul est produits d'idéaux premiers.
Autrement dit : OK est un anneau de Dedekind. De plus, comme dans tout anneau de ce type, une telle décomposition est unique à l'ordre près et tout idéal premier non nul est maximal.
(Les idéaux premiers de ℤ[ω] sont classifiés ci-dessous.)
On définit ensuite une relation d'équivalence sur l'ensemble des idéaux non nuls de OK : A ~ B si et seulement s'il existe des éléments non nuls a, b de OK tels que aA = bB. Les classes s'appellent les classes d'idéaux et forment a priori seulement un monoïde commutatif (classe(A).classe(B) := classe(A.B)) mais en fait un groupe abélien, et même un groupe abélien fini (voir l'article détaillé), appelé le groupe des classes de K. L'anneau OK est principal si et seulement si ce groupe est trivial, c'est-à-dire si h = 1, où le nombre de classes h est l'ordre du groupe.
Le théorème de Chebotarev appliqué au corps de classes de Hilbert H de K (pour lequel le groupe de Galois de H/K est isomorphe au groupe des classes de K) indique que les idéaux premiers se répartissent régulièrement dans chaque classe. Autrement dit : toute classe d'idéaux contient une infinité d'idéaux premiers avec la « densité » 1/h[incompréhensible].
Applications[modifier | modifier le code]
Classification des nombres premiers[modifier | modifier le code]
La structure de l'anneau ℤ[ω] des entiers d'un corps quadratique amène à étudier non pas les diviseurs d'un nombre premier p, mais les facteurs premiers (au sens des idéaux) de l'idéal pℤ[ω]. Cette analyse est utile pour la résolution d'équations diophantiennes.
Il n'y a que trois cas possibles :
Dans ℤ[ω] tout idéal de norme p est premier et il y en a 0, 1 ou 2 ; p est dit :
- inerte s'il y en a 0 (dans ce cas, pℤ[ω] est premier) ;
- décomposé s'il y en a 2 (dans ce cas, ils sont conjugués et pℤ[ω] est leur produit) ;
- ramifié s'il y en a 1 (dans ce cas, il est son propre conjugué et pℤ[ω] est son carré).
Une analyse plus poussée (cf. article détaillé) précise alors dans chacun des trois cas la structure de l'anneau ℤ[ω]/pℤ[ω] et montre que :
- si p ≠ 2 : p est inerte si d n'est pas un carré mod p, décomposé si d est un carré non nul mod p, et ramifié si d est divisible par p (la loi de réciprocité quadratique permet ensuite de discriminer ces trois cas en fonction de la classe de p modulo le discriminant de ℤ[ω], qui vaut d ou 4d) ;
- si p = 2 : p est inerte si d ≡ 5 mod 8, décomposé si d ≡ 1 mod 8 et ramifié sinon.
Équation diophantienne[modifier | modifier le code]
La raison initiale du développement des corps quadratiques est l'étude de l'équation de Pell-Fermat x2 – dy2 = ±1 et plus généralement, de l'équation diophantienne x2 – dy2 = ±p. Illustrons par quelques exemples comment la théorie précédente permet d'en venir à bout lorsque p est un nombre premier. Les cas d = –1 et d = –3 sont traités dans l'article « Théorème des deux carrés de Fermat » et le cas d = 5 dans l'article « Anneau des entiers de ℚ(√5) ». Le cas d = –2 ci-dessous est analogue car dans ces quatre cas, l'anneau est principal donc chercher les éléments de norme p est équivalent à chercher les idéaux de norme p.
x2 + 2y2 = p[modifier | modifier le code]
Chaque idéal de norme p est principal, engendré par un élément x + yi√2 de norme p ou son opposé. On en déduit :
L'équation x2 + 2y2 = p possède dans ℤ2
- 4 solutions (x, y) = ± (a , ±b) si le nombre premier p est congru à 1 ou 3 mod 8
- 2 solutions (0, ±1) si p = 2
- aucune pour les autres valeurs du nombre premier p.
x2 + 5y2 = p[modifier | modifier le code]
Si d est égal à –5, la situation est plus délicate car l'anneau ℤ[i√5] n'est pas principal : son groupe des classes est d'ordre 2. Mis à part les deux cas ramifiés p = 2, qui correspond à l'unique idéal de norme 2 (non principal, car aucun élément de l'anneau n'a pour norme 2), et p = 5, qui fournit les deux solutions triviales (0, ±1), elle se résume de la manière suivante :
Si initialement la méthode est la même que pour le cas d'un anneau principal, il devient nécessaire d'établir la nature des idéaux de norme p. Si l'idéal est principal, une solution existe, sinon la valeur p n'est pas atteinte par la fonction. Le groupe des classes permet de s'en rendre compte. Cette méthode est générale, cependant pour des valeurs importantes de d les calculs s'avèrent fastidieux.
Classification des formes quadratiques[modifier | modifier le code]
Notes et références[modifier | modifier le code]
- (en) John Stillwell, Mathematics and Its History [détail des éditions], 2010, p. 75-77.
- Fermat termine son défi par : « J'attends la solution de ces questions ; si elle n'est fournie ni par l'Angleterre, ni par la Gaule Belgique ou Celtique, elle le sera par la Narbonnaise » (Laurent Hua et Jean Rousseau, Fermat a-t-il démontré son grand théorème ? l'hypothèse "Pascal", L'Harmattan, 2002 (ISBN 978-2-74752836-8), p. 113).
- Ou plus généralement dans un anneau à PGCD.
- Par exemple Bas Edixhoven et Laurent Moret-Bailly, Théorie algébrique des nombres, cours de maîtrise de mathématiques, université de Rennes I, (lire en ligne).
- « Un corps algébrique est un corps qui ne contient que des nombres algébriques. » : p. 8 de O. Ore, « Les corps algébriques et la théorie des idéaux », Mémorial des sciences mathématiques, vol. 64, , p. 1-72 (lire en ligne).
- (en) Kenneth H. Rosen (en) et John G. Michaels, Handbook of Discrete and Combinatorial Mathematics, CRC Press, (ISBN 978-0-8493-0149-0, lire en ligne), p. 295.
- (en) Song Y. Yan, Primality Testing and Integer Factorization in Public-Key Cryptography, New York, NY, Springer, , 2e éd. (ISBN 978-0-387-77268-4, lire en ligne), p. 240.
- Ne pas confondre avec la fermeture algébrique ni avec la clôture intégrale.
- (en) Harvey Cohn, Advanced Number Theory, Dover, (1re éd. 1962), 276 p. (ISBN 978-0-486-64023-5, lire en ligne), p. 45-47.
- Cohn 1980, p. 48.
- Hardy et Wright 2007, p. 266-267 et 279, § 14.4 et 15.1.
- Cette propriété est vraie plus généralement dans tout anneau noethérien.
- Aux interversions près des puissances négatives impaires de ω avec leurs opposés.
- (en) Leonard Eugene Dickson, History of the Theory of Numbers (en) [détail des éditions], vol. 2.
- Bhāskara II, Bijaganita (1150), cf. (en) John J. O'Connor et Edmund F. Robertson, « Pell's equation », sur MacTutor, université de St Andrews..
- J.-L. Lagrange, Solution d'un problème d'arithmétique.
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) David A. Cox, Primes of the Form x2 + ny2, Wiley, (1re éd. 1989) (ISBN 978-1-11803100-1, lire en ligne)
- G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres, Paris/Heidelberg, Vuibert-Springer, , 568 p. (ISBN 978-2-7117-7168-4)
- (en) Kenneth Ireland et Michael Rosen, A Classical Introduction to Modern Number Theory, Springer, coll. « GTM » (no 84), (réimpr. 1998), 2e éd., 389 p. (ISBN 978-0-387-97329-6, lire en ligne)
- Pierre Samuel, Théorie algébrique des nombres [détail de l’édition]
- Jean-Pierre Serre, Cours d'arithmétique, [détail des éditions]
Lien externe[modifier | modifier le code]
(en) Eric W. Weisstein, « Quadratic Field », sur MathWorld









