Géométrie riemannienne

La géométrie riemannienne est une branche de la géométrie différentielle nommée en l'honneur du mathématicien Bernhard Riemann, qui introduisit les concepts fondateurs de variété géométrique et de courbure. Il s'agit de surfaces ou d'objets de plus grande dimension sur lesquels existent des notions d'angle et de longueur, généralisant la géométrie traditionnelle qui se limitait à l'espace euclidien. La géométrie riemannienne étend les méthodes de la géométrie analytique en utilisant des coordonnées locales pour effectuer les calculs dans des domaines spatiaux limités, mais elle recourt fréquemment aux outils de la topologie pour passer à l'échelle de l'espace entier. De façon précise, la géométrie riemannienne a pour but l'étude locale et globale des variétés riemanniennes, c'est-à-dire les variétés différentielles munies d'une métrique riemannienne, voire des fibrés vectoriels riemanniens.
Les concepts les plus notables de la géométrie riemannienne sont la courbure de l'espace étudié et les géodésiques, courbes résolvant un problème de plus court chemin sur cet espace.
Il existe aussi des variétés pseudo-riemanniennes, généralisant les variétés riemanniennes, qui en restent assez proches par bien des aspects, et qui permettent notamment de modéliser l'espace-temps en physique.
Histoire[modifier | modifier le code]
Avènement de la géométrie riemannienne[modifier | modifier le code]

Pendant de nombreux siècles, le cadre naturel de la géométrie est la géométrie euclidienne du plan ou de l'espace. Les infructueuses tentatives de démonstration du postulat des parallèles ont aidé les géomètres à imaginer les moyens de dépasser ce cadre. Ainsi Lobatchevski en 1829 et Bolyai en 1832 introduisent les premiers exemples de géométrie non euclidienne. Les espaces à géométrie hyperbolique qu'ils construisent sont maintenant vus comme des cas particuliers de variétés riemanniennes "à courbure négative".
Quelques années auparavant, Gauss étudie la géométrie différentielle des surfaces de l'espace euclidien. Il introduit pour les décrire une quantité fondamentale, la courbure de Gauss. Il réalise que cette courbure peut être calculée sans faire intervenir l'espace ambiant, directement à partir d'informations disponibles sur la surface, théorème qu'il qualifie de "remarquable" (theorema egregium). Gauss passe lui-même tout près de la découverte de la géométrie hyperbolique.
Le premier pas de la géométrie riemannienne proprement dite remonte aux travaux de Bernhard Riemann au dix-neuvième siècle et en particulier lors d'une conférence inaugurale intitulée Über die Hypothesen, welche der Geometrie zu Grunde liegen[1] (soit en français : Sur les hypothèses sous-jacentes à la géométrie). C'est une généralisation directe de la géométrie différentielle des surfaces de Gauss en n dimensions. Cette nouvelle démarche a largement étendu l'idée de géométrie non euclidienne, même si son cadre conceptuel a mis plusieurs décennies à se mettre en place.
Vers une formalisation complète[modifier | modifier le code]
La deuxième moitié du XIXe siècle verra surtout s'affiner la compréhension de la géométrie hyperbolique, à travers l'introduction et l'analyse de différents modèles de représentation, qui trouveront une application en relativité restreinte. Différents outils apparaissent, qui prouveront progressivement leur grande importance. Ainsi la théorie des groupes et algèbres de Lie apparaît dans les années 1870, alors que parallèlement Felix Klein souligne l'importance du concept de groupe en géométrie dans son programme d'Erlangen. Ulisse Dini prouve son théorème des fonctions implicites qui sera un prélude indispensable à la formalisation des variétés. Henri Poincaré développe profondément le champ de la topologie, et introduit notamment le groupe fondamental.
Un pas décisif est franchi lorsque Gregorio Ricci-Curbastro et Tullio Levi-Civita développent le calcul tensoriel dans leur ouvrage Méthodes de calcul différentiel absolu et leurs applications paru en 1900[2]. Si le cadre "spatial" n'est pas encore totalement éclairci, les calculs progressent grandement grâce aux tenseurs. Une application très profonde est trouvée lorsqu'Einstein, initié aux nouvelles géométries et à ce calcul tensoriel par son ami Marcel Grossmann, les met au service de sa théorie de la relativité générale en 1916.
De 1902 au milieu des années 1930, de nombreuses tentatives de formalisation de la notion de variété différentielle ont lieu. Cette quête se conclut avec la publication du théorème de plongement de Whitney en 1936. La géométrie riemannienne possède enfin un cadre clair.
Un domaine de recherche en expansion[modifier | modifier le code]


La classification des espaces symétriques par Élie Cartan en 1926 est un des premiers grands résultats de géométrie riemannienne. Dans les années 1930 sont publiés les premiers théorèmes généraux sur les variétés à courbure positive (théorème de Bonnet-Schoenberg-Myers, théorème de Synge).
Le théorème de la sphère établi en 1960 marque une forme d'apogée des conceptions classiques à base de théorèmes de comparaisons. S'amorce alors un renouveau de la géométrie riemannienne. Il est marqué par le développement des méthodes de la géométrie spectrale, aiguillonné par la célèbre formule de Mark Kac « Peut-on entendre la forme d'un tambour ? (en) », et dont les liens avec la recherche de géodésiques périodiques sont mis à jour. Dans les années 1980 Mikhail Gromov introduit une notion de distance entre les variétés riemanniennes et prouve des résultats de convergence féconds. À la même époque Richard Hamilton commence à développer l'étude du flot de Ricci, lançant un programme de démonstration de résultats topologiques par la géométrie riemannienne par des méthodes de déformation de métriques. Ce programme connaît de grandes réussites, avec la preuve de la célèbre conjecture de Poincaré par Perelman en 2003 et une généralisation puissante du théorème de la sphère (le "théorème de la sphère différentielle") en 2007.
Les notions fondamentales de la géométrie riemannienne, comme la courbure, trouvent progressivement un cadre d'utilisation bien plus large que celui des variétés riemanniennes proprement dites, et s'étendent sous des formes plus ou moins complexes aux espaces métriques. Gromov définit ainsi les espaces CAT(k) de Cartan-Alexandrov-Toponogov ou encore des notions de théorie géométrique des groupes, comme le groupe hyperbolique. Villani, Lott et Sturm introduisent dans les années 2010 une vision étendue, « synthétique » de la notion de courbure de Ricci minorée à partir d'une formulation de transport optimal sur un espace métrique muni d'une mesure.
Le cadre de la géométrie riemannienne[modifier | modifier le code]
La métrique riemannienne[modifier | modifier le code]
L'objet d'étude de la géométrie riemannienne est la variété riemannienne. Il s'agit d'une variété différentielle munie d'une métrique riemannienne, c'est-à-dire d'un champ tensoriel qui permet, en chaque point de la variété, de calculer le produit scalaire de deux vecteurs de l'espace tangent, et leur norme. Dans un système de coordonnées locales , ce champ s'exprime en chaque point par une expression de la forme et le produit scalaire de deux champs de vecteurs est donné par . On note également le tenseur métrique .
Il existe de nombreux tenseurs g possibles[GHL 1], variant continûment avec la position sur la variété. Cela permet sur une même variété différentielle, d'obtenir des structures riemanniennes très diverses et de définir les notions fondamentales de géodésiques et de courbure, qu'on retrouve notamment en relativité générale.
Calculs de longueur et de distance[modifier | modifier le code]

La métrique riemannienne permet de définir la notion de longueur d'un arc donné par un paramétrage , par la formule .
La distance entre deux points est la borne inférieure des longueurs des arcs joignant ces deux points. Une variété riemannienne est donc notamment un espace métrique. Réciproquement, à partir de l'application distance on peut retrouver la structure différentielle et le tenseur métrique[Pano 1].
La définition qui a été donnée est intrinsèque, c'est-à-dire qu'elle ne fait intervenir que la structure abstraite de variété. Pourtant, parmi les exemples les plus simples de variétés riemanniennes, il y a les sous-variétés d'un espace euclidien E, munies de la métrique riemannienne induite. Il convient de noter que la distance associée à la structure riemannienne ne coïncide pas avec la distance mesurée dans E. Par exemple, pour le cercle unité dans le plan, la distance riemannienne correspond à la longueur de l'arc joignant deux points, tandis que la distance mesurée dans le plan est la longueur de la corde.
Sur une variété riemannienne, on peut en outre définir des notions d'aire, de volume tri-dimensionnel, de forme volume (en ajoutant une orientation), etc.
Dans les énoncés, certaines hypothèses topologiques de base sont faites très régulièrement sur les variétés riemanniennes : hypothèses de connexité et de complétude. En termes imagés, la première hypothèse signifie que la variété est "d'un seul tenant", la seconde qu'il n'y a pas de "trou" dans lequel une particule mobile pourrait disparaître en temps fini. On s'intéresse souvent plus spécifiquement aux variétés compactes, pour lesquelles la distance entre les points ne peut pas dépasser une certaine limite. Ces variétés ont un diamètre et un volume finis.
Structure riemannienne et opérations de base[modifier | modifier le code]
De façon plus précise, la géométrie riemannienne étudie les variétés riemanniennes à isométrie près : le résultat de cette identification est ce qu'on appelle une structure riemannienne.
Le théorème de plongement de Nash affirme que toute variété riemannienne peut être plongée de manière isométrique dans un espace euclidien (de dimension plus grande). Une variété riemannienne abstraite peut donc également être vue comme une sous-variété d'un espace euclidien. Même si ce résultat permet en théorie de se limiter aux sous-variétés de , le point de vue des variétés abstraites définies par un atlas s'est imposé comme la bonne façon de travailler en géométrie différentielle, notamment riemannienne.
Les opérations classiques sur les variétés différentielles s'étendent au cas riemannien : le transport de structure par difféomorphisme, le produit cartésien, les revêtements, certains quotients, certaines formes de chirurgie...
Quelques variantes[modifier | modifier le code]
Il est possible de s'intéresser à des variétés riemanniennes de dimension infinie, modelées sur un espace de Hilbert au lieu d'un espace euclidien. Une autre extension de la géométrie riemannienne, déjà imaginée par Riemann[JJ 1], consiste à introduire des métriques plus générales sur l'espace tangent à la variété. On introduit ainsi la structure de variété finslérienne.
La géométrie sous-riemannienne est une extension de la géométrie riemannienne qui intègre la notion de contraintes : la mesure des distances se fait en considérant seulement les courbes tangentes à une famille d'espaces dits « horizontaux ». Enfin, si on travaille avec un tenseur métrique symétrique, défini, mais non forcément positif, on entre dans le domaine des géométries pseudo-riemanniennes, avec notamment le cas particulier de la géométrie lorentzienne, cadre dans lequel est formulée la théorie de la relativité générale.
On peut également sortir du cadre des variétés. Ainsi la façon dont les distances sont introduites en géométrie riemannienne, à partir de la longueur des courbes, donne lieu à différentes généralisations, comme le concept d'espace de longueur.
Les concepts fondamentaux[modifier | modifier le code]
Géodésiques[modifier | modifier le code]
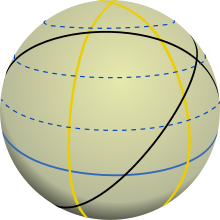

Les géodésiques permettent de répondre à la recherche des plus courts chemins entre deux points, comme le font les droites dans l'espace euclidien. En réalité leurs propriétés sont plus complexes que celles des droites et il convient de distinguer ce qui peut être dit d'un point de vue local, ou de façon plus globale.
Les géodésiques sont définies de façon générale en recourant au calcul des variations[JJ 2]. On considère deux points x et y et l'on étudie la fonctionnelle longueur sur toutes les courbes reliant x à y à vitesse uniforme. Les courbes qui représentent les points critiques de cette fonctionnelle sont qualifiées de géodésiques. On peut de façon équivalente caractériser ces géodésiques par une équation différentielle faisant intervenir le vecteur vitesse , le tenseur g et ses dérivées. On peut aussi introduire ces géodésiques comme les points critiques de l'énergie et les imaginer comme des élastiques tendus sur la variété.
À titre d'exemple, les géodésiques de la sphère sont les grands cercles. Ceci montre que les géodésiques ne réalisent pas toujours la distance minimum entre deux points : pour aller d'un point à un autre, on peut suivre l'arc de grand cercle le plus court ou le plus long, voire les parcourir plusieurs fois. Il n'y a pas non plus unicité du plus court chemin comme on le voit avec deux points diamétralement opposés.
Cependant au niveau local, la situation est bien plus simple. On peut affirmer de façon générale que les géodésiques sont « localement minimisantes » : entre deux de leurs points, pris suffisamment proches, elles réalisent un minimum pour la longueur. Partant d'un point x donné, il existe une unique géodésique de vecteur tangent donné. On peut en fait introduire une carte adaptée centrée en x. Elle est définie par l'application exponentielle en x qui consiste à suivre chacune des géodésiques issues de x pendant un temps unité[GHL 2]. Il y correspond des coordonnées locales adaptées, appelées coordonnées normales.
Pour formuler des résultats globaux, on se placera uniquement dans le cas d'une variété connexe et complète. Dans ce cas, les géodésiques peuvent être prolongées pour tout temps, mais avec des comportements globaux variables (périodicité ou non par exemple). Par ailleurs, entre deux points donnés il existe toujours au moins une géodésique qui réalise le minimum de la longueur : tout ceci constitue le théorème de Hopf-Rinow.
Courbure[modifier | modifier le code]

En géométrie riemannienne, même si les géodésiques généralisent les droites de la géométrie euclidienne, on ne retrouve plus les mêmes résultats concernant les calculs de longueurs, d'angles, de surfaces des objets les plus simples (triangles géodésiques, cercles ou sphères...). Ainsi la somme des angles d'un triangle ne vaut plus forcément 180°, la valeur classique et fixe dans le cadre de la géométrie euclidienne. La courbure permet de quantifier ces écarts.
Dans le cas des surfaces de l'espace euclidien , la courbure est appelée courbure de Gauss. Elle se mesure en chaque point sous la forme d'un scalaire. En un point de courbure positive, la géométrie de la surface ressemble localement à celle d'un ellipsoïde de , et en un point de courbure négative à un hyperboloïde. Un important résultat de Gauss, son theorema egregium, énonce que la courbure peut être entièrement déterminée à partir de la métrique de la surface, c'est-à-dire qu'elle ne dépend pas de la manière dont la surface peut être plongée dans l'espace tridimensionnel.
Plus généralement, on peut, pour toute variété riemannienne, construire un objet complexe appelé tenseur de courbure de Riemann. En coordonnées locales, l'expression de ce tenseur fait intervenir les composantes de g, et leurs dérivées premières et secondes. Le tenseur de courbure est un objet assez complexe à appréhender. Par contraction avec le tenseur métrique on construit des objets plus simples, le tenseur de courbure de Ricci et la courbure scalaire, qui véhiculent une partie importante de l'information.
Une façon de se représenter la notion de courbure est de donner la courbure sectionnelle suivant les différents 2-plans de l'espace tangent à la variété. Il s'agit de la courbure de Gauss de la surface formée par les géodésiques issues de ces deux plans. Cette façon de présenter l'information est équivalente à la donnée du tenseur de courbure. L'idée générale est qu'une courbure sectionnelle positive indique une tendance des géodésiques à se rapprocher les unes des autres, une courbure négative donne une tendance à l'écartement mutuel.
Opérateurs de dérivation[modifier | modifier le code]

Deux notions techniques étroitement liées à la courbure et à la recherche de géodésiques sont la connexion affine et le transport parallèle le long d'une courbe. Ce sont des procédés qui permettent de relier des vecteurs appartenant à des espaces tangents en des points distincts de la variété et, par suite, de dériver des champs de vecteurs. Sur une variété différentielle générale, il n'y a pas de moyen privilégié de faire cela. Il n'est par exemple pas possible de donner un sens au vecteur accélération d'une courbe tracée sur la variété.
La propriété très remarquable des variétés riemanniennes, que Marcel Berger n'hésite pas à qualifier de « miracle »[Pano 2], est qu'il existe une connexion naturellement associée à la métrique, la connexion de Levi-Civita. On montre en effet qu'il existe une unique connexion qui conserve la structure euclidienne quand elle relie les différents espaces tangents et qui donne des différentielles secondes symétriques[Pano 3] : cet énoncé au rôle fondateur est appelé le théorème fondamental de la géométrie riemannienne. A l'aide de la connexion de Levi-Civita, il est possible de « transporter » un vecteur tangent le long d'une courbe donnée. La figure ci-contre montre un exemple d'un tel transport. Mais on peut, plus généralement, faire du calcul différentiel à tout ordre sur tous types de tenseurs.
Le tenseur de courbure de Riemann est défini à partir de la connexion de Levi-Civita, elle-même issue de la métrique g. Dans cette présentation, la courbure peut s'interpréter comme la mesure infinitésimale du défaut de retour à l'origine pour un vecteur qui serait transporté le long d'une courbe fermée. Certains exposés de géométrie riemannienne introduisent également les géodésiques à partir de la notion de connexion[GHL 3].
Il est également possible de construire une généralisation du laplacien pour le cadre riemannien : c'est l'opérateur de Laplace-Beltrami. Il peut être appliqué aux fonctions, ou plus généralement, aux formes différentielles, en utilisant la dualité de Hodge[JJ 3].
Variétés riemanniennes remarquables[modifier | modifier le code]


Des espaces à courbure constante[modifier | modifier le code]
La sphère de dimension n Sn peut être introduite comme l'ensemble des vecteurs de norme donnée dans un espace euclidien de dimension n+1, muni de la métrique induite. On précise parfois qu'il s'agit de la "sphère ronde" ou "sphère euclidienne standard" pour la distinguer des sphères exotiques ou des autres choix de métriques possibles. Il s'agit d'une variété à courbure constante, strictement positive. Elle admet pour géodésiques les grands cercles, et les géodésiques issues d'un point ont la particularité de toutes se recouper au point antipodal. L'identification entre un point et son antipode donne naissance à l'espace projectif réel qui est lui aussi de courbure constante. On peut plus généralement obtenir tous les espaces de courbure constante positive comme quotients de la sphère par un groupe d'isométries agissant discrètement sur la sphère[Pano 4].
De la même façon, l'espace euclidien et ses quotients par des groupes d'isométries fournissent des exemples de variétés à courbure constamment nulle, qualifiées de variétés plates. On obtient ainsi en fait tous les cas, et on peut noter à titre d'exemple le cylindre, le tore « plat » (qui ne peut pas être plongé isométriquement dans l'espace euclidien ) et leur généralisation en toute dimension... On peut même affirmer que toutes les variétés plates compactes sont des quotients finis du tore (théorème de Bieberbach[JJ 4]).
Pour la courbure égale à une constante négative, l'espace modèle est moins familier. Il s'agit de l'espace hyperbolique, dont on peut donner diverses représentations isométriques entre elles : disque ou demi-plan de Poincaré, hyperboloïde de Lorentz ou disque de Klein. Là encore les variétés à courbure constante négative s'obtiennent par quotient à partir de cet exemple.
Par le théorème d'uniformisation de Poincaré, toute variété riemannienne de dimension 2 peut être ramenée, par bijection conforme, à une métrique à courbure constante.
Métrique de Fubini-Study sur l'espace projectif complexe[modifier | modifier le code]
L'espace projectif complexe de dimension n, , peut être vu comme une variété différentielle, quotient de la sphère de dimension 2n+1 par l'action du groupe unitaire U(1)=S1. La métrique induite à partir de la métrique "ronde" sur la sphère par ce passage au quotient est appelée métrique de Fubini-Study. L'espace projectif complexe est un exemple de variété kählérienne compacte, c'est-à-dire qu'elle dispose à la fois d'une structure riemannienne et d'une structure complexe, et d'une structure symplectique qui se déduit des deux précédentes.
La courbure sectionnelle varie entre 1 et 4, selon la formule où est une famille orthonormale de vecteurs tangents et est l'opérateur de la structure complexe. Cette courbure est la plus forte (4) pour les 2-plans holomorphes, c'est-à-dire tels que est colinéaire à , elle vaut 1 lorsqu'à l'opposé et sont orthogonaux. Par ailleurs, le tenseur de Ricci est proportionnel au tenseur métrique, ce qui fait de l'espace projectif complexe un exemple de variété d'Einstein.
Principaux thèmes d'études et résultats[modifier | modifier le code]
Dans son ouvrage A Panoramic View of Riemannian Geometry, le géomètre Marcel Berger propose de présenter les nombreux résultats de géométrie riemannienne sous forme d'un panorama succinct tenant en une page[Pano 5]. Il distingue ainsi les propriétés topologiques et leurs liens avec la courbure, les propriétés métriques, les aspects quantiques de l'étude des variétés riemanniennes, ainsi que les aspects dynamiques. Toutes ces thématiques sont bien entendu interconnectées.
Dans la suite, on ne s'intéresse qu'à des variétés riemanniennes complètes.
Courbure et propriétés métriques[modifier | modifier le code]
Maîtrise de la métrique par la courbure sectionnelle[modifier | modifier le code]

En géométrie euclidienne, on peut calculer la longueur d'un côté du triangle à l'aide des longueurs des deux autres côtés et de l'angle qu'ils forment. Sur une variété riemannienne on peut considérer des triangles géodésiques, mais la formule euclidienne n'est plus vérifiée ; elle fournit une estimation asymptotique au premier ordre sur des triangles infiniment petits, et la courbure sectionnelle donne le terme correctif d'ordre 2. Le théorème de comparaison de Toponogov fournit un résultat global de comparaison : lorsqu'on dispose d'un encadrement de la courbure sectionnelle entre deux constantes m et M, on peut encadrer la longueur du troisième côté entre la valeur qu'elle aurait sur une variété de courbure constante m et celle sur une variété de courbure constante M.
Une courbure sectionnelle minorée par une constante strictement positive impose une forme de refermement des géodésiques. Le théorème de Bonnet-Schoenberg-Myers en donne conséquence globale : la variété possède un diamètre, qui est majoré par .
En sens inverse, on pourrait s'attendre à ce que disposer d'une majoration de la courbure donne un contrôle sur le non refermement des géodésiques. La situation est plus complexe que cela, puisque sur le tore plat par exemple, il existe une géodésique fermée qui peut être de longueur très petite (elle varie suivant les dimensions du tore). On introduit un nouvel outil de contrôle de la métrique, le rayon d'injectivité. Si ce rayon d'injectivité vaut r, l'application exponentielle en chaque point est injective sur la boule B(0,r) de l'espace tangent en m. Elle constitue même un difféomorphisme de cette boule sur la boule B(m,r) pour la métrique de la variété. Un théorème de Klingenberg de 1959 montre que sur une variété compacte à courbure sectionnelle majorée par , le rayon d'injectivité est soit plus grand que soit égal à la moitié de la longueur de la plus petite géodésique périodique[Pano 6].
Intervention de la courbure de Ricci[modifier | modifier le code]
Certains des résultats précédents peuvent être généralisés en ayant uniquement un contrôle sur la courbure de Ricci, ce qui est une hypothèse moins forte. Précisément, l'invariant pertinent est la plus basse valeur propre de la courbure de Ricci. De façon assez naturelle, cet invariant permet de contrôler le comportement du volume. Ainsi l'inégalité de Bishop-Gromov (en) fournit un théorème de comparaison des volumes des boules géodésiques lorsqu'on compare les courbures de Ricci au cas des espaces à courbure constante.
De façon plus inattendue, Mikhail Gromov a initié un programme de recherche de bornes pour les différents invariants riemanniens ne faisant intervenir que la dimension de la variété, son diamètre et la valeur propre minimale de la courbure de Ricci[3].
Des inégalités globales, sans courbure[modifier | modifier le code]

Une des directions de recherche importantes en géométrie riemannienne est l'établissement d'inégalités globales entre les grandeurs métriques, sans faire intervenir la maîtrise locale de la courbure. On peut ainsi, pour toute variété compacte de dimension d, comparer directement volume et rayon d'injectivité, élevé à la puissance d-ième pour que cette comparaison ait un sens. Ainsi Berger a prouvé en 1980 que pour toute variété compacte, on peut minorer le rapport de ces deux grandeurs, et cela en ne faisant intervenir que la dimension d. Il propose d'appeler constante embolique de la variété la borne inférieure sur toutes les métriques
et démontre que cette constante est toujours supérieure à celle de la sphère, tandis que dans le cas de la sphère, c'est la métrique standard qui réalise la borne inférieure. La valeur des constantes emboliques en dimension 3 et plus, même pour des variétés très simples, n'est pas connue[Pano 7].
Une autre grandeur métrique sur laquelle on recherche des inégalités et une comparaison avec le volume est la systole, c'est-à-dire la longueur minimale d'une courbe non contractile (toujours élevée à la puissance d). Le cas des surfaces a été abondamment étudié, ainsi l'inégalité torique de Loewner répond à la question dans le cas du tore et peut être vue comme une forme d'inégalité isopérimétrique. Il n'est pas possible de trouver une minoration universelle analogue à celle évoquée pour les constantes emboliques et la sphère, comme le montre le cas des produits . Cependant Gromov a prouvé en 1983 une inégalité pour une large classe de variétés compactes de dimension d, les variétés essentielles[Pano 8].
Courbure et topologie[modifier | modifier le code]
Dans le cas des surfaces compactes, le lien entre la courbure et la topologie est donné par la célèbre formule de Gauss-Bonnet. L'intégrale de la courbure (scalaire, ou sectionnelle, cela revient au même) suffit alors à décrire la variété. Mais en dimension plus grande, la situation est plus complexe.
Résultats généraux selon le signe de la courbure[modifier | modifier le code]
Sous des hypothèses de positivité de la courbure, on peut également tirer des conclusions sur la topologie. Si la courbure est minorée par une constante strictement positive, une conséquence du théorème de Bonnet-Schoenberg-Myers est que la variété est compacte, avec un groupe fondamental fini. Le théorème de Synge décrit plus précisément la situation dans le cas d'une dimension paire.
Il existe des variétés riemanniennes non compactes à courbure positive (à titre d'exemple : les paraboloïdes ou les cylindres de l'espace euclidien). Pour une telle variété M, si la courbure reste strictement positive, la variété est difféomorphe à . Si la courbure est positive au sens large, M possède une "âme", c'est-à-dire une sous-variété totalement géodésique telle que M est difféomorphe au fibré normal à cette sous-variété. C'est un théorème de Cheeger-Gromoll de 1972[Pano 9].
Si la variété est à courbure négative, le théorème de Cartan-Hadamard prouve que l'application exponentielle en un point m quelconque fournit un revêtement de la variété. Si elle est simplement connexe, la variété est donc difféomorphe à . Et de façon plus générale, une variété à courbure négative peut être vue comme un quotient de par un groupe discret.
Sur une variété compacte à courbure strictement négative, le groupe fondamental est finiment engendré mais à croissance exponentielle[Pano 10].
Caractérisation de la topologie par la courbure : problèmes de pincement[modifier | modifier le code]
Sous des hypothèses de courbure suffisamment fortes, il est possible de caractériser la topologie de la variété sous-jacente, voire sa structure différentielle. Le résultat le plus célèbre est sans doute le théorème de la sphère établi en 1960 par Rauch, Berger et Klingenberg, et selon lequel une variété complète et simplement connexe dont la courbure reste dans un intervalle de la forme ]A,4A] avec A>0 est homéomorphe à une sphère. Le cas limite où la courbure est dans [A,4A] est également caractérisé. Cette hypothèse sur la courbure est souvent qualifiée de "pincement" dans la littérature.
Ce résultat a été considérablement étendu en 2007 par Brendle et Schoen, avec une hypothèse moins forte de pincement "ponctuel" (rapport entre les courbures sectionnelles maximale et minimale en un même point) et une conclusion plus forte : la variété est difféomorphe à la sphère ordinaire.
En 1978 puis 1982, Gromov et Ruh obtiennent une caractérisation des variétés compactes presque plates, c'est-à-dire dont la courbure est "pincée près de 0" (au sens suivant : le produit de la courbure et du carré du diamètre est inférieur à une constante ne dépendant que de la dimension). Cependant il n y a pas que les tores et leurs quotients, on obtient plus généralement une infranilvariété[JJ 5].
Des outils de contrôle plus grossiers[modifier | modifier le code]
Les théorèmes de pincement forment une famille de résultats aux hypothèses très exigeantes et aux conclusions puissantes. Il existe un point de vue plus "grossier"[GHL 4] dans lesquels on essaye de montrer que des hypothèses assez lâches sur la courbure permettent déjà de limiter fortement les types topologiques possibles. Ainsi quand on fixe des bornes a priori sur le diamètre et la valeur absolue de la courbure, et une valeur minimale pour le volume, on peut prouver que les variétés qui peuvent porter des métriques respectant ces contraintes sont en nombre fini, à difféomorphisme près[JJ 6].
Gromov a introduit une généralisation de la distance de Hausdorff pour étudier une notion de convergence des métriques riemanniennes modulo les isométries. Il a établi qu'en se plaçant sur l'ensemble des structures vérifiant des bornes du même type que précédemment, on pouvait affirmer que toute suite de métriques admettait une sous-suite convergente, du moins au sens de la régularité [JJ 7].
Aspects quantiques : spectre d'une variété[modifier | modifier le code]
Spectre du laplacien[modifier | modifier le code]

Sur les variétés riemanniennes compactes il est possible de procéder à une forme d'analyse harmonique très proche de la théorie des séries de Fourier. On étudie en effet les valeurs propres et vecteurs propres de l'opérateur de Laplace-Beltrami sur les fonctions. Il s'agit des fonctions f et des scalaires vérifiant la relation , et on prouve que les valeurs propres forment une suite infinie appelée spectre de la variété. Les différents espaces propres associés sont orthogonaux et de dimension finie, celui associé à étant formé des fonctions constantes[4].
Les fonctions propres du laplacien forment une base hilbertienne permettant de décomposer les fonctions définies sur la variété, et de résoudre des équations aux dérivées partielles (équation de la chaleur, équation d'onde, équation de Schrödinger) par des démarches proches de celles employées dans le cas euclidien : séparation des variables d'espace et de temps et recherche de solutions fondamentales par décomposition sur la base des vecteurs propres du laplacien. S'y ajoutent cependant des difficultés techniques nouvelles.
Le spectre lui-même est un objet d'étude important. Il donne lieu à deux types d'étude classiques : les problèmes directs qui consistent à donner des estimations sur le spectre à partir des autres données géométriques, et les problèmes inverses qui, a contrario, cherchent à retrouver des éléments géométriques à partir du spectre. Un des résultats principaux reliant les deux types de données est la généralisation de la formule asymptotique de Weyl estimant le nombre (compté avec la multiplicité) de valeurs propres inférieures ou égales à :
Le problème inverse fait l'objet de recherches actives depuis le début des années 1960, avec l'apparition de la question isospectrale : « deux variétés riemanniennes de même spectre sont-elles isométriques ? », à laquelle Milnor a répondu par la négative en 1964. Il n'y a pas non plus de caractérisation des spectres effectivement réalisables ; en revanche on sait construire sur toute variété compacte de dimension au moins 3 une métrique ayant un spectre imposé jusqu'à un rang donné[Pano 12].
Géodésiques fermées et spectre des longueurs[modifier | modifier le code]
Les géodésiques sont dites fermées quand elles sont périodiques, c'est-à-dire qu'elles repassent par un même point avec un même vecteur vitesse. Le spectre des longueurs d'une variété compacte est l'ensemble des longueurs de ses géodésiques fermées.
L'existence et le comptage de telles géodésiques fermées est un objet de recherches important. En 1951, Lusternik et Fet montrent que sur toute variété compacte il existe au moins une telle géodésique fermée[JJ 8] : c'est le théorème de Lusternik-Fet. Même dans le cas, simple en apparence, de la sphère de dimension 2 munie d'une de ses métriques, il est difficile de préciser le nombre de géodésiques fermées. En 1929, Lusternik et Schnirelmann prouvent qu'on peut toujours trouver au moins trois géométriques fermées géométriquement distinctes et qui sont des courbes simples. On ne peut en trouver plus, comme le montrent certains ellipsoïdes. Mais si on ne demande plus que ces courbes soient simples, on peut en trouver une infinité, selon un théorème de 1993 de John Franks et Victor Bangert[Pano 13], popularisé par la formule « un million de façons de placer un élastique sur une pomme de terre »[5].
On sait depuis 1959 que, pour les surfaces de Riemann, spectre des longueurs et spectre du laplacien se déterminent l'un l'autre. La preuve s'appuie sur la formule des traces de Selberg. En dimension plus grande, on peut toujours dire que le spectre du laplacien détermine le spectre des longueurs, d'après un résultat de Colin de Verdière de 1973[Pano 14].
Aspects dynamiques[modifier | modifier le code]
Flot géodésique[modifier | modifier le code]
Les géodésiques d'une variété riemannienne peuvent être vues comme des valeurs extrêmales de l'énergie. Elles sont donc solution d'un problème de moindre action et peuvent s'interpréter en termes physiques comme des trajectoires de particules qui ne sont soumises à aucune force. L'étude du flot géodésique permet de préciser la dynamique d'ensemble. Une des questions qui entrent dans ce cadre est l'existence et le comptage des trajectoires périodiques, c'est-à-dire de géodésiques fermées, problème mentionné précédemment.
Les variétés compactes à courbure strictement négatives ont un flot géodésique qui se comporte de façon extrêmement chaotique. En utilisant la terminologie des systèmes dynamiques, ce flot est ergodique et mélangeant ; en termes imagés, en suivant ce flot sur un temps long, un ensemble donné est « dispersé » de façon équitable dans toute la variété (au sens de la mesure). Savoir s'il est possible de trouver un exemple de variété à courbure positive qui réalise elle aussi l'ergodicité est une question ouverte[Pano 15].
Flots géométriques[modifier | modifier le code]

Depuis les années 1980, le champ d'application des flots géométriques s'est considérablement étendu. Celui qui a donné les résultats les plus féconds dans le domaine de la géométrie riemannienne proprement dite est le flot de Ricci, mais d'autres types de flots ont été introduits et ils ont eu également des répercussions dans des domaines tels que la physique théorique, l'analyse d'image ou l'optimisation par exemple. La caractéristique commune des flots géométriques est de ne pas étudier une métrique fixée, mais de déformer les objets géométriques suivant une équation d'évolution qui fait intervenir elle-même des quantités géométriques telles que la courbure. On arrive ainsi typiquement à des équations d'évolution de type équation aux dérivées partielles paraboliques. On profite ainsi du pouvoir régularisant de ces équations, qui a tendance à « arrondir » la métrique étudiée, à la rapprocher de situations modèles simples.
Le flot de Ricci consiste à partir d'une métrique donnée et à suivre l'équation d'évolution . Il est possible d'établir l'existence de solutions localement en temps. Richard Hamilton a élaboré un plan d'attaque pour avancer vers des résultats de topologie des variétés en petite dimension à l'aide du flot de Ricci, notamment la célèbre conjecture de Poincaré et la conjecture de géométrisation, plus forte. Le premier grand succès de la théorie a été de montrer qu'une variété de dimension 3 à courbure de Ricci strictement positive évolue vers une métrique de courbure constante, en 1982[6]. Deux ans après , un résultat analogue est établi pour les variétés de dimension 4 à opérateur de courbure strictement positif. Une difficulté qui a été résolue progressivement est l'apparition de zones singulières, des "zones d'étranglements" dans lesquelles la métrique s'effondre numériquement en temps fini. Ces singularités ont été analysées et dépassées par des techniques de chirurgie rendues compatibles avec l'équation d'évolution. Les deux plus grands résultats obtenus par le flot de Ricci sont sans doute la preuve de la conjecture de géométrisation par Perelman en 2003[7],[8] et la généralisation du théorème de la sphère prouvée par Schoen et Brendle en 2007[9].
Hamilton a également introduit un autre type de flot géométrique sur les variétés compactes, appelé flot de Yamabe. Dans ce cas l'équation d'évolution fait intervenir la valeur moyenne de la courbure scalaire et a l'avantage de conserver la structure conforme. Hamilton a cette fois prouvé un théorème d'existence de la solution pour tout temps et a formulé la conjecture que la métrique converge vers une métrique à courbure scalaire constante, c'est-à-dire une solution du problème de Yamabe. Ce résultat n'a été établi que sous des hypothèses restrictives sur la dimension ou la métrique initiale[10].
Un autre type de flot géométrique consiste à faire évoluer une variété plongée. Ainsi le flot de courbure moyenne (en) permet de rapprocher une surface d'une surface minimale plongée en dimension 3. Ces surfaces minimales correspondent en termes géométriques à une minimisation locale de l'aire (à la façon dont les géodésiques minimisent localement la distance), et on peut les comprendre en termes physiques comme une minimisation de la tension de surface. Plus généralement ce flot peut être utilisé pour des hypersurfaces en toute dimension.
Structures additionnelles[modifier | modifier le code]
Sur certaines variétés riemanniennes, il est possible d'introduire des structures additionnelles qui sont compatibles avec la structure riemannienne et viennent l'enrichir. On construit ainsi différentes formes de géométries nouvelles (kählérienne, spinorielle, etc.), possédant chacune des propriétés et des objets propres qui complètent le cadre riemannien. Selon des conceptions bien établies depuis le programme d'Erlangen de Félix Klein, à chacune de ces géométries est associée l'action d'un groupe particulier.
Un des exemples les plus simples est le choix d'orientation, quand la variété riemannienne est orientable. Il permet de définir le fibré des repères orthonormaux orientés et la forme volume. Le groupe d'intérêt est alors le groupe spécial orthogonal.
On peut aussi considérer les structures Spin et Spinc définies sur certaines variétés riemanniennes orientables. Quand elles existent, elles donnent une sorte de « dédoublement » de la géométrie riemannienne, permettant d'introduire le concept de spineur et un opérateur de Dirac (en), sorte de racine carrée du laplacien[11],[12].
Les variétés kählériennes portent trois structures compatibles, qui les font relever de la géométrie riemannienne, de la géométrie symplectique et de la géométrie complexe. Ce domaine d'étude très riche utilise simultanément les outils des trois domaines, et possède des caractéristiques propres, comme les notions de courbure holomorphe et courbure bisectionnelle, ou des opérateurs et sur les formes différentielles tels que la différentielle extérieure se scinde en et de la même façon les groupes de cohomologie se scindent[JJ 9]. On obtient des résultats de structure très forts, ainsi le fait qu'une variété kählérienne à courbure bisectionnelle strictement positive est biholomorphe à l'espace projectif complexe[Pano 16].
Il existe également des structures plus exigeantes encore : on définit la notion de variété hyperkählérienne (en) et celle de variété quaternion-kählérienne (en), qui portent toutes deux une structure rappelant les quaternions. Elles apparaissent dans la classifications des groupes d'holonomie effectuée par Marcel Berger et James Simons[Pano 17].
Applications[modifier | modifier le code]
À d'autres domaines des mathématiques[modifier | modifier le code]

Toute variété différentielle peut être munie d'une structure riemannienne. Celle-ci peut servir d'intermédiaire pour établir des résultats dont la formulation ne fait pas intervenir de concept proprement riemannien. C'est le cas de la conjecture de Poincaré déjà mentionnée, qui est un résultat de topologie pure dont la démonstration utilise largement la déformation de métriques riemanniennes. C'est également le cas de la théorie de Morse qui relie la topologie d'une variété différentielle aux lignes de niveau des fonctions définies sur cette variété, en exploitant la dynamique des lignes de gradient associées à une certaine métrique.
Certains concepts introduits en géométrie riemannienne ont été étendus à des domaines d'application plus large, dans le cadre des espaces métriques. On peut par exemple généraliser la notion de géodésique dans un graphe, notamment un graphe pondéré. On s'intéressera plus particulièrement aux espaces métriques géodésiques, pour lesquels il y a unicité du plus court chemin entre deux points. Alors qu'en géométrie riemannienne on utilisait une estimation sur la courbure sectionnelle pour obtenir un résultat de comparaison des distances entre les points de deux triangles isométriques, sur ces espaces métriques on peut renverser la démarche. On définit une notion de "courbure majorée par k" ou "courbure minorée par k" à partir de la comparaison des triangles. Cette idée est à la base de l'introduction des espaces CAT(k) de Cartan-Alexandrov-Toponogov. Ces espaces ont par ailleurs l'avantage, contrairement aux variétés riemanniennes, d'être compatibles avec la convergence pour la distance de Gromov-Hausdorff.
Des considérations du même type peuvent être appliquées aux groupes finiment engendrés lorsqu'on les munit de la métrique des mots. Pour ces groupes, les propriétés algébriques, géométriques et arithmétiques s'interpénètrent. Ainsi un théorème de Gromov caractérise les groupes de type fini pour lesquels la croissance des boules est polynomiale. Un objet d'étude important est le groupe hyperbolique, pour lequel on a des triangles δ-fins pour tout réel δ>0.
Les définitions précédentes montrent comment étendre l'idée de courbure sectionnelle à un cadre plus large, sans utiliser les propriétés de régularité fortes que demande le cadre riemannien. Cette approche a été qualifiée de synthétique par opposition à l'introduction traditionnelle de la courbure sectionnelle, dite analytique. La dualité des approches apporte des éclairages différents, et des possibilités d'aller-retour fructueux. À partir des années 2000 ont été progressivement mises au point des théories synthétiques pour la courbure de Ricci. Elles se sont basées sur la découverte d'un lien entre courbure de Ricci, théorie du transport et entropie, suivie là aussi d'un renversement de la démarche : Cédric Villani, John Lott et Karl-Theodor Sturm ont introduit une version étendue de la notion de courbure de Ricci minorée à partir d'une formulation de transport optimal sur un espace métrique muni d'une mesure[13],[14].
À la mécanique et la relativité[modifier | modifier le code]
La théorie de la relativité se déroule dans un cadre très proche de celui de la géométrie riemannienne, celui d'une variété lorentzienne. Il s'agit d'une variété de dimension 4 munie d'un tenseur métrique qui n'est plus défini positif, mais de signature (en) (3,1). L'équation d'Einstein indique la façon dont la courbure est reliée à la masse et à l'énergie représentées par le tenseur énergie-impulsion. C'est pourquoi on trouve une très grande parenté de concepts et d'idées et de fortes interactions entre géométrie riemannienne et physique théorique, même si chacune poursuit des objectifs propres. C'est ainsi qu'Arthur Besse, pseudonyme collectif, justifiant l'intérêt de l'étude des "variétés d'Einstein" pour les géomètres riemanniens, évoque la question des liens avec la physique
« Clarifions notre objectif. Nous employons le terme "variétés d'Einstein" pour des variétés riemanniennes à courbure de Ricci constante parce que c'est la convention en vigueur chez les mathématiciens depuis longtemps. Nous ne prétendons pas travailler pour les physiciens théoriciens. Par ailleurs, face à notre domaine d'étude, ces derniers se répartissent en deux groupes. Le premier estime que ce que nous faisons n'a aucun intérêt. Le second pense que les variétés riemanniennes (et par exemple les variétés riemanniennes d'Einstein) peuvent leur apporter quelque aide, ne serait-ce qu'à titre d'inspiration. Ou même leur être véritablement utiles, en plaçant l'ensemble de l'étude dans un tableau plus vaste par un procédé de complexification, de façon à faire disparaître la question des différences de signe. Les mêmes remarques peuvent être faites au sujet de la théorie de Yang-Mills[15] »
Notes et références[modifier | modifier le code]
- Version originale et traduction en anglais.
- Biographie de Tullio Levi-Civita par J. J. O'Connor et E. F. Robertson sur le site McTutor de l'université de St Andrews
- (en) Arthur Besse, Einstein Manifolds, coll. « Ergebnisse der Mathematik und ihrer Grenzgebiete » (3), vol. 10, Springer-Verlag, Berlin, 1987, p. 17.
- Il y a en réalité deux conventions couramment utilisées pour définir l'opérateur de Laplace, différant par le signe. Avec l'autre convention, les valeurs propres seront négatives. Voir par exemple Berger 2003, p. 377.
- Ian Stewart, Science: A million ways to wrap a rubber band round a potato, New Scientist, 2 janvier 1993.
- Richard S. Hamilton, « Three-manifolds with positive Ricci curvature », J. Diff. Geom, vol. 17, , p. 255–306.
- Description et schéma de la preuve dans (en) John W. Morgan, « Recent progress on the Poincaré conjecture and the classification of 3-manifolds », Bull. Amer. Math. Soc., vol. 42, no 1, , p. 57-78.
- Validation et preuve détaillée par Bruce Kleiner et John Lott (en) dans Notes on Perelman's papers (en), publié dans Geometry & Topology, volume 12, pp. 2587-2855, 2008.
- Simon Brendle et Richard Schoen, « Curvature, Sphere Theorems, and the Ricci Flow », Bull. Amer. Math. Soc., vol. 48, no 1, , p. 1-32 (DOI 10.1090/s0273-0979-2010-01312-4, MR 2738904, arXiv 1001.2278).
- (en) Simon Brendle et Fernando Marques, Recent progress on the Yamabe problem, (ISBN 978-7-04-032732-8).
- (en) Nicolas Ginoux, Spinc structures on manifolds, novembre 2012.
- (en) H. Blaine Lawson et Marie-Louise Michelsohn, Spin Geometry, PUP, , 427 p. (ISBN 978-0-691-08542-5), p. 123.
- Les travaux de Cédric Villani, Julie Rehmeyer, sur le site Images de mathématiques, CNRS
- Cédric Villani, Optimal transport, old and new, p. 502-503,755
- Arthur Besse, Einstein manifolds, p. 4
- (en) Sylvestre Gallot, Dominique Hulin et Jacques Lafontaine, Riemannian Geometry [détail de l’édition]
- Théorème 2.2 p. 49.
- Définition 2.86 p. 81.
- Définition 2.77 p. 77.
- En reprenant l'expression employée par les auteurs p. 147.
- (en) Marcel Berger, A Panoramic View of Riemannian Geometry, [détail de l’édition]
- Marcel Berger attribue la paternité de cette réciproque à Richard Palais en 1957, voir p.174.
- P. 697.
- P. 698 et 705.
- Théorème 69 p. 252 et remarque p. 253.
- P. 219.
- Théorème 89 p. 272 et commentaire qui suit.
- P. 355-357.
- P. 345.
- Théorème 331 p. 584.
- Théorème 104 p. 306.
- Théorèmes 164 p. 386 et 172 p. 401.
- Théorème 186 p. 415.
- Théorème 233 p. 468
- Pages 405 et 421.
- Question 254 p. 488.
- Théorème 402 p. 656
- Théorème 397 p. 643 et figure 13.4 p. 646.
- (en) Jürgen Jost, Riemannian Geometry and Geometric Analysis, [détail des éditions]
- P. 31.
- Définition 1.4.2 p. 17.
- Définition 2.1.2. p. 83.
- P. 227.
- P. 228.
- Finiteness theorem p. 229.
- Convergence theorem p. 229.
- Théorème 6.11.4 p. 368.
- p. 236-240
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Marcel Berger, A Panoramic View of Riemannian Geometry, [détail de l’édition]Comme l'indique son titre, le grand géomètre français nous convie ici à une longue (824 pages) promenade panoramique dans le monde de la géométrie riemannienne ; les divers résultats sont pour la plupart donnés sans démonstrations détaillées, mais avec les références idoines pour le lecteur qui souhaiterait mettre « les mains dans le cambouis » ; le dernier chapitre donne les bases techniques du domaine.
- (en) Jürgen Jost, Riemannian Geometry and Geometric Analysis, [détail des éditions]
- (en) Lizhen Ji, Athanase Papadopoulos et Sumio Yamada (eds.), From Riemann to Differential Geometry and Relativity, Springer, , xxxiv+647 (ISBN 978-3-319-60039-0, lire en ligne)





![{\displaystyle \gamma :[a,b]\rightarrow M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c4ba7eb5ea03868d9299512c02190eae635b87)



























