Géométrie hyperbolique
En mathématiques, la géométrie hyperbolique (nommée auparavant géométrie de Lobatchevski, lequel est le premier à en avoir publié une étude approfondie) est une géométrie non euclidienne vérifiant les quatre premiers postulats d’Euclide, mais pour laquelle le cinquième postulat, qui équivaut à affirmer que par un point extérieur à une droite passe une et une seule droite qui lui est parallèle, est remplacé par le postulat selon lequel « par un point extérieur à une droite passent plusieurs droites parallèles à celle-ci » (il en existe alors une infinité).
En géométrie hyperbolique, la plupart des propriétés métriques de la géométrie euclidienne ne sont plus valables ; en particulier le théorème de Pythagore n'est plus vérifié, et la somme des angles d'un triangle est toujours inférieure à 180°. Les droites restent cependant les lignes de plus court chemin joignant deux points, ce qui a permis à Beltrami, dans le cas du plan hyperbolique, de les modéliser comme des géodésiques sur une surface de courbure constante négative, comme les droites de la géométrie elliptique sont modélisées par des grands cercles sur une sphère.
À la suite de Beltrami, Klein et Poincaré ont construit plusieurs autres modèles de géométrie hyperbolique, comme le modèle de l'hyperboloïde ou celui du disque de Poincaré. Ces modèles montrent l'indépendance de l'axiome des parallèles, c'est-à-dire l'impossibilité de le démontrer (ou de le réfuter) à partir des autres axiomes ; cela revient également à dire que si la géométrie euclidienne ne contient pas de contradiction, il en est de même de la géométrie hyperbolique.
La détermination de la « vraie » géométrie de notre espace physique s'est posée dès la découverte des géométries non euclidiennes ; au début du XXIe siècle, les tests expérimentaux ne permettent toujours pas de décider ce qu'il en est, ce qui constitue le problème de la platitude, l'une des questions non résolues de la cosmologie.
Historique[modifier | modifier le code]
- Les pères de la géométrie hyperbolique
Le cinquième postulat d'Euclide (appelé actuellement « axiome des parallèles »[note 3]) semble avoir toujours eu un statut bien moins « naturel » que celui des quatre autres, et avoir plutôt été ressenti comme un théorème dont la démonstration n'avait pas encore été obtenue[2]. Des tentatives de démonstration apparaissent dès l'Antiquité[note 4], et de nombreuses « preuves » erronées en existent. La piste la plus prometteuse pour le déduire des autres semble être de raisonner par l'absurde, et plusieurs mathématiciens ont cru avoir réussi, obtenant en niant le postulat des résultats qui leur paraissaient en effet contredire le bon sens[note 5], tels que le fait que deux droites perpendiculaires à une même droite s'éloigneraient l'une de l'autre dans les deux directions. Cependant, les échecs de ces tentatives allaient progressivement amener à l’idée que d’autres géométries étaient possibles, et à la découverte des géométries non euclidiennes.
L'histoire de la géométrie hyperbolique proprement dite semble cependant ne commencer qu'au début du XVIIIe siècle avec les travaux du mathématicien italien Giovanni Girolamo Saccheri[4], qui cherche à démontrer dans l'œuvre de sa vie, Euclides ab omni naevo vindicatus (Euclide lavé de toute tache), que les postulats d'Euclide sont cohérents et nécessaires pour définir la géométrie. Supposant notamment faux le cinquième postulat, il tente de développer toutes les conséquences de cette hypothèse, jusqu'à obtenir une contradiction. Il échoue dans cette tentative, obtenant une grande quantité de théorèmes étranges[note 5], mais ne présentant entre eux aucune incohérence. Ne réalisant pas qu'il a sous les yeux une nouvelle géométrie, il conclut son ouvrage par l’aveu d’un demi-échec[note 6].
Au milieu du XVIIIe siècle, Jean-Henri Lambert étudie lui aussi les conséquences de la négation du postulat, et obtient sous cette hypothèse des théorèmes et des résultats précis (considérés désormais comme appartenant à la géométrie hyperbolique), comme la formule donnant la somme des angles d'un triangle en fonction de sa surface : CΔ = π – (α + β + γ), où α, β, γ sont les angles des trois sommets du triangle, C un coefficient de proportionnalité, et Δ la surface du triangle. Vers la fin de sa vie, il semble qu'il ait réalisé que ces théorèmes manifestent l'existence d'une authentique géométrie « sur une sphère de rayon imaginaire »[4],[note 7].
Ce sont les travaux de Carl Friedrich Gauss qui sont généralement reconnus comme étant le véritable point de départ de la géométrie hyperbolique, bien que ceux-ci n'aient jamais été publiés de son vivant[note 8]. Il formule dans ses notes, dès 1813, une théorie structurée[7], et il semble qu'il avait pleinement conscience que cette géométrie avait un statut mathématique équivalent à celui de la géométrie euclidienne[8],[note 9].
La géométrie hyperbolique est redécouverte et explorée de manière extensive par Nikolaï Lobatchevski à partir de 1830[10],[11], et indépendamment par János Bolyai, dès 1825, dans des travaux publiés en 1831[12] ; cependant, ces travaux n’obtiennent qu'une reconnaissance très tardive, lorsqu'est publiée en 1865 la correspondance entre Gauss et Heinrich Christian Schumacher[13], dans laquelle Gauss dit le plus grand bien de Lobatchevski et de Bolyai[14].
La géométrie hyperbolique est considérée comme une curiosité sans vraie importance pratique (Lobatchevski l'appelle « géométrie imaginaire », au sens où elle s'oppose à la géométrie réelle de l'espace physique[note 10]), jusqu'à ce que Eugenio Beltrami en propose en 1868 plusieurs modèles (qu'il appelle des représentations), parmi lesquelles les représentations conforme et projective, redécouvertes par la suite respectivement par Henri Poincaré et Felix Klein, ainsi que le modèle de la pseudosphère[note 11]. Il démontre, à l’aide de ces représentations, que si la géométrie euclidienne est mathématiquement cohérente, alors la géométrie hyperbolique l'est aussi nécessairement, et donc que l’axiome des parallèles est indépendant des autres[16],[note 12].
En 1872, Felix Klein montre, dans le programme d'Erlangen, que toutes les géométries, euclidiennes et non euclidiennes, peuvent être vues comme des sous-géométries de la géométrie projective, en utilisant une conique (dite conique absolue) privilégiée (cette construction est celle qui définit la métrique de Cayley-Klein) ; le choix d'une conique « réelle » comme conique absolue permet de construire la géométrie de Lobatchevski[note 13] et explique en partie le nom de « géométrie hyperbolique » que Klein lui donne[note 14] et qui lui est désormais associé[note 15],[19],[20].
Géométrie du plan hyperbolique[modifier | modifier le code]
Cette section ne détaille que les propriétés des figures planes[21] ; en effet, la géométrie de l'espace hyperbolique en dimension supérieure peut se déduire de celle du plan comme dans le cas euclidien, et il n'y apparaît pas de phénomènes essentiellement nouveaux[note 16].
Géométrie absolue[modifier | modifier le code]

Les propriétés du plan qu'on peut démontrer à partir des axiomes d'Euclide (ou d'une formulation plus rigoureuse et moderne, telle que celle de Hilbert), à l'exception de l'axiome des parallèles, sont dites appartenir à la géométrie absolue. Ainsi, par exemple, on montre que deux perpendiculaires à une même droite n'ont pas de points communs[note 17], et donc qu'il existe toujours des parallèles (c'est pourquoi la géométrie elliptique n'est pas une géométrie absolue). De nombreuses propriétés de la géométrie hyperbolique coïncident de même avec celles de la géométrie euclidienne, parfois au prix d'une reformulation : ainsi, on démontre aisément que les bissectrices intérieures d'un triangle quelconque sont concourantes (la démonstration classique n'utilise pas la notion de parallèles), et donc qu'il existe un cercle inscrit dans ce triangle ; les propriétés des médiatrices amèneraient à penser qu'elles sont également concourantes et donc qu'il existe également un cercle circonscrit, mais ce résultat est faux en général dans le plan hyperbolique, car deux perpendiculaires à deux droites concourantes peuvent être parallèles ; ce qui reste vrai, c'est que si deux médiatrices d'un triangle se coupent, les trois médiatrices sont concourantes (le même résultat est également vrai pour les hauteurs du triangle)[note 18].
Parallèles[modifier | modifier le code]

On obtient la géométrie hyperbolique à partir de la géométrie absolue en remplaçant l'axiome des parallèles (ou plus exactement la version qu'en a donné Proclus[note 3]) par un axiome affirmant par exemple que « il existe au moins deux droites concourantes parallèles à une même troisième ». On démontre alors que pour toute droite D et pour tout point P non sur D, il existe une infinité de droites passant par P et ne rencontrant pas D, situées entre deux droites limites formant un angle 2θ ne dépendant que de la distance de P à D ; θ est appelé angle de parallélisme (le calcul de cet angle en fonction de la distance sera fait dans la section consacré aux propriétés métriques)[24]. Les deux droites limites sont dites parallèles asymptotes à D (certains auteurs réservent le terme de parallèles aux parallèles asymptotes ; les autres droites non sécantes sont alors dites ultraparallèles, ou parfois hyperparallèles). On démontre[note 19] que si deux droites du plan sont non sécantes (parallèles au sens euclidien usuel), ou bien elles sont asymptotes, ou bien il existe une et une seule droite perpendiculaire aux deux ; le segment découpé sur cette perpendiculaire commune correspond alors à la distance minimale entre ces deux droites (laquelle est nulle pour deux droites asymptotes). Les notions euclidiennes de direction d'une droite, définie comme relation d'équivalence entre droites parallèles, et de point à l'infini d'une droite (défini, en géométrie projective, comme l'intersection de cette droite avec la droite de l'infini) disparaissent, mais il reste possible de définir une relation d'équivalence entre parallèles asymptotes (les droites possédant désormais deux directions) ainsi qu'une notion de points à l'infini ; par exemple, dans le modèle du disque de Poincaré, les points à l'infini forment un cercle limitant le disque et chaque droite (représentée dans ce modèle par un arc de cercle) coupe ce cercle limite en deux points correspondant à ses deux directions, deux droites étant parallèles asymptotes si elles ont un point à l'infini en commun[25].
Cercles et pseudo-cercles[modifier | modifier le code]



Les propriétés métriques d'un cercle de rayon r diffèrent de celles du plan euclidien : son périmètre et son aire sont respectivement supérieurs à 2πr et à πr2. Mais de plus, certaines propriétés caractéristiques des droites euclidiennes définissent des courbes du plan hyperbolique qui n'ont pas d'analogue euclidien, mais qui par certains côtés peuvent s'interpréter comme des cercles généralisés : les points situés à une distance fixe d d'une droite donnée D forment une courbe appelée un hypercycle ; les courbes dont les normales en tout point forment une famille de droites asymptotiquement parallèles sont appelées des horocycles (ou parfois horicycles[20]). Dans le modèle du disque de Poincaré, les cercles, les horocycles et les hypercycles (ainsi que les droites) sont tous représentés par des cercles ou des arcs de cercle. Par trois points formant un triangle passe une courbe unique de cette famille (un cercle, un horocycle ou un hypercycle), qui généralise donc la notion de cercle circonscrit à ce triangle. Enfin, si une suite de points Pn () est telle que les segments Sn = [PnPn+1] sont tous de même longueur et que les angles entre ces segments sont tous égaux et suffisamment grands[note 20], elle forme un polygone régulier infini, appelé un apeirogone régulier, inscrit dans un horocycle ou dans un hypercycle[26].
Polygones réguliers et pavages[modifier | modifier le code]
L’angle au sommet d’un polygone régulier à n côtés (qui vaut n–2nπ dans le plan euclidien) dépend de la longueur a du côté en géométrie hyperbolique et peut être rendu aussi petit que l’on veut[note 21] ; c’est pourquoi on peut paver de manière uniforme le plan hyperbolique avec des polygones réguliers d'un nombre quelconque de côtés, et avec n'importe quel nombre de polygones ayant un sommet commun[27] (alors qu'il n'existe dans le plan euclidien que trois pavages réguliers). L'exemple ci-contre représente (dans le modèle du disque de Poincaré) un pavage par des pentagones réguliers ayant cinq angles droits.
Propriétés métriques[modifier | modifier le code]
Contrairement au plan euclidien, il existe une échelle absolue des longueurs dans le plan hyperbolique, analogue au rayon de la sphère en géométrie sphérique, et qu'on peut interpréter comme une « courbure », une déformation du plan euclidien rendant par exemple la somme des angles d’un triangle inférieure à 180°. Gauss a défini, plus généralement, une notion de courbure intrinsèque pour une surface quelconque, en n'utilisant que des lignes tracées sur la surface ; avec cette définition, on démontre que le plan hyperbolique est une surface de courbure constante négative K[28]. En choisissant convenablement l'unité de longueur, on peut prendre K égal à –1 ; c'est cette convention qui sera utilisée dans la suite. Pour des formules plus générales, il faudrait multiplier par –K toutes les longueurs y apparaissant ; ainsi, dans le cas général, la relation entre les côtés d’un triangle rectangle devient cosh(Kc) = cosh(Ka) cosh(Kb), et l'aire d'un disque de rayon r est .
Angle de parallélisme[modifier | modifier le code]
Si P est un point hors de la droite D et H son projeté orthogonal sur D (avec a = HD la distance de P à D), les formules données ci-dessous pour un triangle rectangle PHM, avec M sur D s'éloignant à l'infini, aboutissent à la formule donnant le sinus de l'angle de parallélisme θ, formule découverte par Lobatchevski[29] :
- .
Cet angle tend très rapidement vers 0 lorsque P s'éloigne de D, c'est-à-dire que la plupart des droites passant par P sont parallèles à D[24].
Aires[modifier | modifier le code]

Le périmètre d'un cercle de rayon r est 2π sinh(r) = π(er – e–r) et l'aire du disque correspondant est 2π(cosh(r) – 1) ; ainsi, l'aire d'un disque croît beaucoup plus vite avec son rayon que dans le plan euclidien[30]. Il en va tout autrement de l'aire Δ d'un triangle (dont les angles α, β et γ sont d'autant plus petits que les côtés sont grands) : Lambert a démontré que Δ = π – (α + β + γ), formule identique au signe près à la formule de Girard en trigonométrie sphérique, et qui montre au passage que la somme des angles d'un triangle est toujours inférieure à π[31].
Trigonométrie du triangle hyperbolique[modifier | modifier le code]
Formellement, on peut obtenir les résultats correspondant au plan hyperbolique en supposant le triangle tracé sur une sphère de rayon imaginaire R = i (c'est-à-dire que R2 = –1)[note 22] ; en d'autres termes, en remplaçant dans les formules classiques de la trigonométrie sphérique les sinus et les cosinus des arcs (et non ceux des angles) par les sinus et cosinus hyperboliques (et en corrigeant certains signes). Ainsi, pour un triangle ABC, avec les mêmes conventions que dans le cas sphérique (côtés notés a = BC, b = AC et c = AB ; angles correspondants notés α, β et γ), on a une loi des cosinus : cosh(c) = cosh(a) cosh(b) – sinh(a) sinh(b) cos(γ), une loi des cosinus duale : cos(γ) = – cos(α) cos(β) + sin(α) sin(β) cosh(c), et une loi des sinus : [32]. En particulier, pour un triangle rectangle en C, on a cosh(c) = cosh(a) cosh(b) ; comme cosh(x) ≈ 1 + x22 pour x suffisamment petit, on retrouve à la limite le théorème de Pythagore[33].
Triangle idéal[modifier | modifier le code]

Une autre figure n'ayant pas d'analogue euclidien est obtenue en éloignant indéfiniment les sommets d'un triangle ordinaire : on obtient à la limite trois parallèles asymptotes deux à deux, les sommets étant rejetés à l'infini. Tous les triangles obtenus ainsi, appelés triangles idéaux, sont isométriques, et, ayant leurs trois angles nuls, ont (d'après la formule de Lambert) une aire égale à π, la plus grande possible pour un triangle[34].
Déplacements du plan hyperbolique[modifier | modifier le code]
On appelle déplacement du plan une isométrie qui conserve l'orientation. Les rotations du plan hyperbolique sont définies exactement comme en géométrie euclidienne : si r est la rotation de centre C et d'angle α, l'image de A par r, A' = r(A) est le point tel que CA' = CA et que l'angle ; la démonstration de ce que cette transformation est bien un déplacement ne dépend pas de l'axiome des parallèles. En revanche, il n'existe pas de vrais analogues des translations en géométrie hyperbolique ; ce qui s'en rapproche le plus est une rotation autour d'un point à l'infini C, transformation formée du composé de deux symétries orthogonales ayant pour axes deux droites concourantes en ce point (donc parallèles asymptotes) ; dans les itérations d'une telle transformation, chaque point parcourt les sommets d'un apeirogone régulier inscrit dans un horocycle de centre C (cette transformation est parfois appelée une horolation de centre C). Plus généralement, on démontre que tout déplacement du plan hyperbolique est composé de deux symétries orthogonales : c’est l'identité si les axes de symétrie sont confondus, c’est une rotation ordinaire s'ils se coupent, c’est une horolation s'ils sont parallèles asymptotes, et enfin, si les deux axes de symétrie sont ultraparallèles, ce déplacement est une translation le long de leur perpendiculaire commune, les autres points parcourant des hypercycles ayant pour axe cette perpendiculaire[35].
Géométrie analytique[modifier | modifier le code]
L'invention par René Descartes des systèmes de coordonnées qui portent son nom a donné naissance à la géométrie analytique, permettant de résoudre des questions de géométrie à l'aide des méthodes de l'algèbre[36],[37]. Il est possible de repérer de même les points du plan hyperbolique par des couples de nombres, le système le plus usité étant celui des coordonnées axiales (prenant pour coordonnées d'un point ses projections orthogonales sur deux axes perpendiculaires)[38], mais ces systèmes sont loin d'être aussi commodes, en raison de la complexité des formules décrivant les figures usuelles (droites et cercles) ou permettant de calculer angles et distances ; c'est pourquoi la plupart des applications informatiques passent plutôt par des calculs dans le modèle du disque de Poincaré[note 23].
Modèles de la géométrie hyperbolique[modifier | modifier le code]
La théorie des modèles trouve précisément sa source dans les exemples construits par Eugenio Beltrami, qui leur donnait le nom de représentations[40] ; pour lui, une représentation d'une géométrie est une construction, dans l'espace euclidien usuel (ou plus généralement dans l'espace ), d'objets correspondant de manière cohérente à une géométrie et ses propriétés. Par exemple, le diagramme de Minkowski est une représentation de la géométrie minkowskienne ; la sphère munie de ses grands cercles forme une représentation de la géométrie elliptique. Beltrami a utilisé les différentes représentations qu'il avait obtenues pour démontrer rigoureusement l'indépendance de l'axiome des parallèles[16],[note 12].
Toutes les représentations de la géométrie hyperbolique sont équivalentes d'un point de vue mathématique[note 24], c'est-à-dire qu'il existe des isomorphismes permettant de passer d'une représentation à une autre ; c'est à ce sens que les mathématiciens parlent du plan hyperbolique comme d'un objet unique[note 25].
Pour s'assurer de ce que les différentes représentations données ci-dessous sont bien des modèles de la géométrie hyperbolique (autrement dit qu'ils en vérifient tous les axiomes), il ne suffit pas de dire ce qu'en sont les « droites » ; il faut aussi y définir une notion de congruence (des segments), ou, ce qui revient au même, une distance entre les points[note 26] (qui sera nécessairement différente de la distance ordinaire de l'espace). On trouvera les formules définissant ces distances pour chaque modèle dans les articles détaillés correspondants[note 27].
Modèle de Klein[modifier | modifier le code]

Dans ce modèle, l'espace hyperbolique est une boule ouverte euclidienne. En dimension 2, le plan hyperbolique est donc modélisé par un disque ouvert. Les droites de l'espace hyperbolique sont des segments dont les extrémités appartiennent au bord de la boule ; la distance est donné par la métrique de Cayley-Klein. La représentation des droites hyperboliques est aisée dans ce modèle, mais les angles ne sont pas conservés et les cercles sont représentés par des ellipses.
La sphère (ou le cercle en dimension 2) limitant le domaine du modèle correspond à des points de l'espace hyperbolique situés à l'infini. Aussi, plus on s'approche du bord du domaine et plus les distances ont l'air de se contracter dans le modèle.
Disque de Poincaré[modifier | modifier le code]
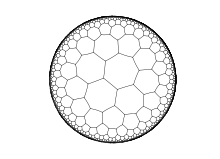
Comme dans le modèle de Klein-Beltrami, l'espace hyperbolique est représenté dans ce modèle par une boule ouverte euclidienne (et donc par un disque en dimension 2), mais les droites de cet espace hyperbolique sont des arcs de cercles perpendiculaires au bord de la boule ; la distance est définie par la métrique de Poincaré. L'intérêt de cette représentation est que, localement, la métrique de l'espace est, à un facteur près, la métrique euclidienne du modèle. En particulier, l'angle entre deux droites de l'espace hyperbolique est égal à l'angle de la géométrie euclidienne formé par les deux arcs de cercles du modèle représentant ces deux droites. On dit que la représentation de l'espace hyperbolique est conforme.
Comme dans le modèle de Klein-Beltrami, la sphère (ou le cercle en dimension 2) limitant le domaine du modèle correspond à des points de l'espace hyperbolique situés à l'infini, les distances semblant se contracter lorsqu'on s'approche du bord du domaine.
Demi-plan de Poincaré[modifier | modifier le code]

Dans ce modèle, l'espace hyperbolique est un demi-espace ouvert de . En dimension 2, le plan hyperbolique est donc modélisé par un demi-plan euclidien. Les droites de cet espace hyperbolique sont des arcs de cercles perpendiculaires à l'hyperplan (ou à la droite en dimension 2) limitant le demi-espace ; la distance est définie à l'aide de la métrique La représentation est là aussi conforme.
Dans ce modèle, l'hyperplan (ou la droite en dimension 2) limitant le domaine correspond à des points de l'espace hyperbolique situés à l'infini. Les distances se contractent en s'approchant de cet hyperplan, et se dilatent en s'en éloignant.
Modèle de l'hyperboloïde[modifier | modifier le code]
Dans ce modèle, étudié par Poincaré et surtout par Killing dans les années 1880[41], l'espace hyperbolique est une nappe d'un hyperboloïde muni d'une métrique particulière. Plus précisément, dans l'espace de Minkowski, c'est-à-dire Rn+1, muni de la pseudo-métrique –dx2
0 + dx2
1 + ... + dx2
n, c'est la nappe de l'hyperboloïde d'équation x2
0 – x2
1 – ... – x2
n = 1 telle que x0 > 0, munie de la pseudo-métrique induite, qui est en fait une métrique riemannienne homogène. Minkowski a montré en 1908 que ce modèle s'identifiait à l'espace des vecteurs-vitesse (Geschwindigkeitsvectoren) de la relativité restreinte[42].
Représentation de Beltrami[modifier | modifier le code]


Eugenio Beltrami a proposé en 1868 de prendre une surface de courbure constante négative comme modèle du plan hyperbolique (et d'appeler « droites » les géodésiques de cette surface)[43],[note 11]. Il est impossible (d'après un théorème de Hilbert) d'obtenir ainsi un modèle du plan hyperbolique tout entier qui ne présente pas de singularités, mais la pseudosphère en est la meilleure représentation ; elle présente de plus l'avantage de conserver la métrique usuelle, en mesurant les distances le long des géodésiques. Henri Poincaré a démontré plus généralement l'équivalence du plan hyperbolique avec toute surface « abstraite » (techniquement, toute variété riemannienne de dimension 2) de courbure négative constante complète et simplement connexe munie de ses géodésiques ; ce résultat est un cas particulier de son théorème d'uniformisation.
Géométrie hyperbolique en dimension quelconque[modifier | modifier le code]

Pour définir l'espace hyperbolique de dimension n, noté Hn, il est possible de reprendre l'approche axiomatique (en s'appuyant par exemple sur les axiomes de Hilbert) ; d'autre part, la définition de Felix Klein se généralise aisément en dimension quelconque en remplaçant la conique absolue par une hyperquadrique[44].
Cependant, les définitions modernes préfèrent s'appuyer sur la notion de variété riemannienne[22] : Hn est une variété riemannienne de dimension n, simplement connexe symétrique, ayant une courbure sectionnelle constante et négative (toutes les variétés vérifiant ces propriétés sont isomorphes, et même isométriques[note 28]). Les « droites » sont les géodésiques de cette variété, et par chaque point passe au moins une sous-variété isomorphe au plan hyperbolique étudié précédemment[45] ; c'est cette approche qui amène, réciproquement, à se demander quelles géométries sont compatibles avec une variété donnée (et en particulier quelles conditions sont nécessaires pour qu'elle puisse être munie d'une géométrie hyperbolique) ; ces recherches ont culminé en 2003 avec la démonstration par Grigori Perelman de la conjecture de géométrisation de Thurston.
Une troisième approche, plus constructive, consiste à définir Hn comme étant l'un des modèles ci-dessus (lesquels sont tous isomorphes entre eux), le modèle de l'hyperboloïde pour la simplicité des calculs, ou celui de Poincaré, conforme, pour des représentations graphiques commodes. Le modèle de l'hyperboloïde, en particulier, peut être défini comme quotient d'un espace de matrices, ce qui lui donne une riche structure algébrique, et facilite l'étude de ses isométries[note 29].
Plusieurs approches purement géométriques ont également été proposées ; d'une part, l'axiomatique de Bachmann, construite en 1959 en n'utilisant que les notions d'incidence[note 30], d'orthogonalité et d'isométrie[20]; d'autre part, la découverte au début des années 2000 d'une structure algébrique, l'espace gyrovectoriel, jouant pour la géométrie hyperbolique le même rôle que la structure d'espace vectoriel joue pour la géométrie euclidienne[47].
Plus généralement encore, Mikhaïl Gromov a découvert vers 1985 les espaces métriques hyperboliques, des espaces ayant des propriétés similaires à celles de l'espace hyperbolique, et qui sont définis à l'aide d'une relation entre leurs distances, le produit de Gromov[48].
Applications[modifier | modifier le code]

Groupe modulaire[modifier | modifier le code]

Le groupe modulaire agit naturellement sur le plan hyperbolique, plus particulièrement sur les représentations de Poincaré ; c'est un sous-groupe de son groupe des déplacements, représenté dans ces modèles par les transformations de Möbius. Les courbes modulaires sont définies comme quotients du plan hyperbolique par certains sous-groupes du groupe modulaire ; les classes d'équivalence correspondantes amènent à des pavages du plan hyperbolique, étudiés en particulier par Poincaré, Dedekind et Klein[49].
Dynamique chaotique[modifier | modifier le code]
Le flot géodésique sur une variété riemannienne compacte à courbure négative est le prototype de système dynamique à temps continu le plus chaotique qui soit, une propriété remarquée dès 1898 par Hadamard[50]. On sait aujourd'hui que ce flot est bernoullien[51], et donc en particulier ergodique, mélangeant (« mixing »), etc.[52],[53]. De nombreuses études détaillées de ce flot et de ses applications ont été publiées à partir de la fin des années 1980[58].
Théorie de la complexité[modifier | modifier le code]
La théorie de la complexité, sous sa forme usuelle, suppose un monde où les signaux se propagent instantanément, et où, par conséquent, la lecture d'une donnée prend toujours le même temps. Mais des analyses plus fines ont été proposées ; il a alors été remarqué que dans un monde hyperbolique, on peut stocker beaucoup plus d'informations à distance donnée, ce qui permet d'accélérer certains calculs ; en particulier, on peut démontrer que, dans cet espace, P = NP[note 31] (cela ne permet pas de démontrer le résultat dans un espace euclidien dans lequel d'ailleurs, très probablement, P est différent de NP)[59].
Relativité restreinte et physique quantique[modifier | modifier le code]
Dès 1908, Hermann Minkowski a remarqué que l'espace des vecteurs-vitesses de la relativité restreinte se comportait comme le plan hyperbolique (c'est le modèle de l'hyperboloïde)[42]. La composition des vitesses donne naissance ainsi à une structure algébrique appelée espace de gyrovecteurs, définie et étudiée à partir des années 2000 par plusieurs auteurs dont Abraham A. Ungar[47], et qui a trouvé des applications en géométrie hyperbolique proprement dite, mais aussi, par exemple, dans l'étude de la sphère de Bloch[60].
Cosmologie[modifier | modifier le code]
Gauss, puis Lobatchevski, ont envisagé que la géométrie de l'espace physique ne soit pas euclidienne[note 9],[note 10], mais les mesures géodésiques et même astrométriques qu'ils ont pu réaliser[note 32] n'ont fait que confirmer l'axiome des parallèles. La question a été reprise d'un point de vue physique lorsque Einstein a formulé sa théorie de la relativité générale, dont le modèle suppose que les masses « courbent » l'espace. Déterminer la géométrie de l'espace dans son ensemble, et en particulier sa courbure[note 33], devient alors une question susceptible de tests expérimentaux, utilisant en particulier le fait que dans un espace hyperbolique, le volume d'une sphère croit beaucoup plus vite que le cube de son rayon. Au début du 21e siècle, l'espace semble cependant « plat » (euclidien) à la précision des mesures[61], ce que nos connaissances physiques actuelles n'expliquent pas bien : c’est le problème de la platitude[note 34]. Pourtant, certains cosmologistes, comme Jean-Pierre Luminet, ont proposé, sous le nom d'« univers chiffonné »[63], des modèles d'univers dont certains sont dérivés de l'espace hyperbolique H3 (en en construisant un espace quotient)[65], et qu'ils affirment compatibles avec les données observationnelles[66].
Dans la culture[modifier | modifier le code]
Littérature[modifier | modifier le code]
Si beaucoup de textes de science-fiction et de fantastique font référence à des géométries non-euclidiennes (Lovecraft mentionnant à plusieurs reprises que leur utilisation dans l'architecture par les Grands Anciens rend fous ceux qui essaient de la comprendre[67]), il semble que seul le roman de Christopher Priest, Le Monde inverti, se déroule dans un univers (la surface d'une caténoïde) à géométrie hyperbolique. On peut cependant également citer le Géométricon, une bande dessinée racontant les aventures d'Anselme Lanturlu dans des espaces courbes, parmi lesquels figure le plan hyperbolique[68].
Art[modifier | modifier le code]

Maurits Escher, grâce aux outils que lui a fourni Harold Coxeter en 1952, a utilisé à plusieurs reprises des pavages du plan hyperbolique en transformant leurs motifs pour en faire des figures anthropomorphiques ou des animaux, comme dans Anges et Démons[69], ou dans la série des Limites circulaires[70].
S’inspirant de modèles conçus et réalisés en papier par le géomètre William Thurston[71], Daina Taimiņa a inventé une technique de représentation en crochet de portions du plan hyperbolique, utilisée de manière artistique par Margaret et Christine Wertheim pour imiter des récifs coralliens[72].
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Cette illustration ne correspond pas à la pseudosphère étudiée par Beltrami, mais à une autre surface à courbure négative constante, qui en a les mêmes propriétés.
- Un théorème de Hilbert montre d’ailleurs qu'il est impossible de représenter globalement le plan hyperbolique par une surface de l'espace usuel.
- Euclide énonce le cinquième postulat sous une forme particulièrement opaque (« si une droite, tombant sur deux droites, fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits. ») ; dès l'Antiquité, plusieurs versions en ont été démontrées équivalentes (en admettant les autres postulats). La forme actuelle de l'axiome des parallèles (« par un point pris hors d'une droite, il passe une droite et une seule ne la rencontrant pas. ») est due à Proclus, au 5e siècle[1].
- On recense ainsi des reformulations du postulat et des essais de preuves par Archimède et Ptolémée, puis par Alhazen et Omar Khayyam[3].
- Saccheri déclare à leur sujet : « L'hypothèse de l'aigu est absolument fausse, car ces résultats répugnent à la nature de la ligne droite. »[5].
- Saccheri explique qu'il ne lui reste plus qu'à montrer rigoureusement que l'existence de ce que nous appelons des hypercycles est absurde, mais qu'il n'y est pas parvenu[5].
- Ce résultat ne peut se justifier rigoureusement qu'à l'aide, par exemple, du modèle de l'hyperboloïde[4] ; cela correspond, dans l'interprétation du plan hyperbolique comme une surface de courbure négative K, à prendre K = –1/|R|, où R est le rayon (imaginaire) de la sphère.
- Gauss écrit à Bessel avoir renoncé à cette publication « par crainte des cris des Béotiens »[6].
- Gauss a déclaré que ses mesures géodésiques de la somme des angles d'un triangle (qu'il trouvait égale à 180°, à 2 secondes d'arc près) confirmaient l'axiome des parallèles[9], ce qui a amené certains auteurs à penser qu'il envisageait que la géométrie réelle de l'univers puisse être non euclidienne[8].
- Dans la préface de son article de 1837, Géométrie imaginaire[10], Lobatchevski prend soin d'expliquer que « toutes les mesures astronomiques [qu'il a pu faire] ne donnent pas de prise à ce que le monde qui nous entoure soit soumis à cette géométrie. Il faut donc prendre le terme imaginaire au sens de « issu de l’imagination » ou « en dehors du réel ». »
- En 1840, Ferdinand Minding avait obtenu des relations trigonométriques pour la pseudosphère identiques à celles du plan hyperbolique, mais c'est Beltrami qui fit le lien entre ces résultats et ceux de Lobatchevski[15].
- Supposons une contradiction en géométrie hyperbolique, par exemple une preuve de ce qu'il existe deux droites distinctes ayant deux points communs ; dans une représentation (le disque de Poincaré, pour fixer les idées), ces deux droites (représentées par des arcs de cercles orthogonaux au cercle unité) auront également deux points communs, ce qui est impossible pour ces arcs de cercles en géométrie euclidienne. Ainsi, si la géométrie euclidienne est non contradictoire, il en est de même de la géométrie hyperbolique, et donc l'axiome des parallèles ne peut être démontré en géométrie absolue, puisque la géométrie hyperbolique le contiendrait, lui et sa négation. Ce type d'argument est caractéristique des premiers résultats de la théorie des modèles, culminant avec le théorème de complétude de Gödel.
- Dans le plan projectif réel, il n'existe (à transformation projective près) que trois sortes de coniques : les coniques réelles (qui, par un choix convenable de repère, ont pour équation celle du cercle unité, x2 + y2 – z2 = 0), les coniques imaginaires (d'équation x2 + y2 + z2 = 0), et les coniques dégénérées, dont celle d'équation x2 + y2 = 0[17], les deux derniers choix permettant de construire respectivement la géométrie sphérique et la géométrie euclidienne.
- Klein identifie par analogie la conique absolue avec la droite de l'infini de la géométrie projective ; de même que cette dernière est coupée respectivement par les hyperboles, les paraboles et les ellipses en 2, 1 et 0 points, la conique absolue est coupée par les droites en 2 points si elle est réelle (« géométrie hyperbolique »), 1 point si elle est dégénérée (« géométrie parabolique » ou euclidienne), et 0 point si elle est imaginaire (« géométrie elliptique »)[18].
- Dans les pays de l'ex-URSS, elle continue souvent à être appelée « géométrie lobatchevskienne »[14].
- À l'exception peut-être des questions de pavages : s'il est possible de paver uniformément l'espace hyperbolique H3 par des polyèdres réguliers, et même de plus de façons que pour l'espace euclidien, Ernest Vinberg a démontré que, contrairement au cas euclidien, il n'existe pas de pavages uniformes en dimension supérieure à 30[22].
- Par symétrie autour de la perpendiculaire commune, ces droites auraient sinon deux points d'intersection.
- Cependant, même si le centre du cercle circonscrit et l'orthocentre existent, ils ne sont pas alignés, en général, avec le centre de gravité du triangle[23].
- C'est le théorème des ultraparallèles ; David Hilbert a donné une construction géométrique explicite de la perpendiculaire commune.
- On doit avoir (pour tout n) , où θ est l'angle de parallélisme en Pn+1 à la médiatrice de Sn ; l'apeirogone est inscrit dans un horocycle si α = 2θ, et dans un hypercycle si α > 2θ.
- Plus précisément, cet angle vaut , qui tend très rapidement vers 0 quand a devient grand.
- Ce résultat, déjà deviné par Jean-Henri Lambert, peut se justifier rigoureusement à l'aide du modèle de l'hyperboloïde[4].
- C'est par exemple la méthode utilisée par le site de géométrie hyperbolique de l'université de Glasgow[39].
- Cependant, en fonction des usages, les calculs ou les graphiques seront plus aisés à effectuer dans certaines de ces représentations.
- Il faut toutefois préciser que chaque modèle apporte avec lui une définition de la distance entre deux points exprimée dans une unité arbitraire ; on choisit en général cette unité de telle sorte que la courbure soit égale à –1.
- En principe, il faudrait aussi définir l'angle entre deux droites, mais en géométrie hyperbolique, les angles d'un triangle sont entièrement déterminés par les longueurs de ses côtés, et par la courbure de l'espace.
- Les formules définissant la métrique pour chaque modèle sont relativement simples ; la distance, en revanche, est obtenue dans le cas général par l'intégration de cette métrique le long d'une géodésique, ce qui peut amener à des formules très lourdes. Il est cependant possible de simplifier ce calcul, en géométrie hyperbolique, en exploitant les relations métriques dans un triangle bien choisi ; par exemple, dans le modèle du disque de Poincaré, la distance entre les vecteurs du plan u et v s'exprime par la formule où est la norme euclidienne.
- Plus exactement, entre deux de ces variétés, il existe une bijection f et une constante k telle que la distance d (mesurée le long des géodésiques) vérifie d(f(A),f(B)) = k d(A,B) pour tout couple de points A et B.
- Plus précisément, Hn peut s'écrire , où O(k) est le groupe orthogonal d'ordre k, et où O(1,n) est le groupe orthogonal généralisé des matrices laissant invariant le pseudo-produit scalaire de Minkovski en dimension n+1[46].
- En géométrie, on parle d'incidence pour regrouper les notions d'inclusion (un point est incident à une droite, une droite est incidente à un plan) et d'intersection (deux droites non parallèles d'un même plan sont incidentes).
- Il s’agit en fait de la classe des problèmes solubles en temps polynomial par calcul parallèle ; dans un espace euclidien, [59].
- Gauss annonce avoir mesuré la somme des angles d'un triangle de plusieurs dizaines de kilomètres de côté, obtenant 180° à 2 secondes d'arc près[9] ; Lobatchevski signale, dans son article Géométrie imaginaire[10], que sur un triangle de base Terre-Soleil, « la somme des angles diffère de deux angles droits de moins de 0,0003 seconde d'arc [10−10 radians] ».
- Dans les modèles les plus utilisés, l'espace est supposé (à grande échelle) homogène et isotrope ; cela implique qu'il est de courbure constante, et que sa géométrie est hyperbolique, euclidienne ou elliptique selon que cette courbure est négative, nulle ou positive.
- Mentionné dès 1969 par Robert Dicke[62], le problème vient de ce que si l'Univers est à peu près euclidien aujourd'hui, il devait l'être encore bien plus au début de l'expansion ; les modèles d'inflation ont été conçus pour résoudre cette difficulté (et quelques autres, comme le problème de l'horizon), mais ils ne font pas encore consensus dans la communauté scientifique en 2021.
Références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Hyperbolic geometry » (voir la liste des auteurs).
- Proclus de Lycie (trad. P. Ver Eecke), Les commentaires sur le premier livre des Éléments d'Euclide, Bruges, .
- (en) Florence P. Lewis, « History of the Parallel Postulate », The American Mathematical Monthly, vol. 27, no 1, , p. 16–23 (DOI 10.2307/2973238, JSTOR 2973238).
- Boris A. Rosenfeld et Adolf P. Youshkevitch, « Géométrie », dans Histoire des sciences arabes : mathématiques et physique, t. 2, Seuil, , p. 186 et suivantes.
- Roger Penrose, À la découverte des lois de l'univers, Odile Jacob, 2007, chap 2.4.
- (en) John J. O'Connor et Edmund F. Robertson, « Giovanni Girolamo Saccheri », sur MacTutor, université de St Andrews.
- « da ich das Geschrei der Böotier scheue », lettre de Gauss à Bessel du 27 juin 1829, citée dans (de) H. Reichardt, Gauß und die Anfänge der nicht-euklidischen Geometrie, Springer-Verlag, , 250 p. (ISBN 978-3-7091-9511-6, lire en ligne), p. 40.
- A. Dahan-Dalmedico et J. Peiffer, Une histoire des mathématiques : Routes et dédales, [détail des éditions], chap. 4, Figures, espaces et géométries, section 11 : les géométries non euclidiennes p. 154.
- (en) Jeremy Gray, Ideas of Space : Euclidean, Non-Euclidean and Relativistic [détail des éditions].
- (en) Ernst Breitenberger, « Gauss's Geodesy and the Axiom of parallels », Archive for History of Exact Sciences, vol. 31, no 3, , p. 273-289 (lire en ligne).
- Nikolaï Lobatchevski, « Géométrie imaginaire », Journal für die reine und angewandte Mathematik, vol. 17, , p. 295-320 (lire en ligne, consulté le ).
- (ru) Nikolaï Lobatchevski, Пангеометрия, Société mathématique européenne, (première édition en russe, édition française en 1856 sous le titre Pangéométrie ou Précis de géométrie fondée sur une théorie générale et rigoureuse des parallèles).
- (en) « Biographie de János Bolyai », sur Université de St Andrews, (consulté le ).
- Conférence sur l'histoire de la géométrie non euclidienne, par Jean-Daniel Voelke.
- Christian Houzel et Jean-Pierre Bourguignon, « Les écoles russes de mathématique et de physique théorique », France Culture.com Continent sciences par Stéphane Deligeorges (consulté le )
- (en) John J. O'Connor et Edmund F. Robertson, « Ferdinand Minding », sur MacTutor, université de St Andrews..
- Eugenio Beltrami, « Essai d'interprétation de la géométrie noneuclidéenne », Ann. École Norm. Sup. 6, , p. 251–288 (lire en ligne)
- Christian Blanchet, « Cours de géométrie, Chapitre 5.3 (coniques projectives), », sur imj-prg.fr, le site de l'Institut de mathématiques de Jussieu – Paris Rive Gauche.
- (en) Norbert A'Campo et Athanase Papadopoulos, « On Klein’s So-called Non-Euclidean geometry », , page 18.
- « Programme d'Erlangen : définition et explications », sur techno-science.net.
- Yves Martin, « Axiomatique de Bachmann », sur univ-irem.fr (consulté le ).
- La plupart des formules et des résultats de cette section (avec leurs démonstrations) figure sur le site interactif de géométrie hyperbolique de l'université de Glasgow.
- Jos Leys, « Une chambre hyperbolique », sur Images des mathématiques (consulté le ).
- (en) Jeffrey R. Klus, « The Euler Line in Hyperbolic Geometry » : une analyse numérique de ces questions, dans le modèle du disque de Poincaré.
- (en) Eric W. Weisstein, « Angle of Parallelism », sur MathWorld
- Une présentation intuitive de ces idées figure sur le site de Xavier Hubaut, « Qu'y a-t-il à l'infini d'un plan ? », sur xavier.hubaut.info ; on trouvera des démonstrations rigoureuses dans l'article de Jacques Lafontaine, « Introduction à la géométrie hyperbolique », Séminaire de Théorie spectrale et géométrie (Grenoble), , p. 108 et suivantes (lire en ligne).
- Tous les résultats de cette sous-section sont démontrés dans (en) Harold Coxeter, Introduction to Geometry, John Wiley & Sons, , « §16.6 Circles, horocycles, and equidistant curves », p. 300 et suivantes.
- Voir cette liste (et le tableau l'illustrant) (en) sur la Wikipédia anglophone.
- Pierre Pansu, « Cours de géométrie différentielle (chapitre 5 : surfaces à courbure constante) », sur universite-paris-saclay.fr.
- (en) H.P. Manning, Introductory Non-Euclidean Geometry, New York, Dover Publications, , p. 58.
- (en) « Circonférence et aire des cercles hyperboliques », sur le site de l'université de Glasgow.
- (en) « Aire hyperbolique », sur le site de l'université de Glasgow.
- (en) Saul Stahl, The Poincaré Half-plane : A Gateway to Modern Geometry, Jones and Bartlett (lire en ligne), chap. 8 (« The Trigonometry of the Hyperbolic Triangle »), p. 119-129
- (en) « Trigonométrie du triangle hyperbolique », sur le site de l'université de Glasgow.
- (en) Dylan Thurston, « 274 Curves on Surfaces, Lecture 5 », (consulté le )
- Henri Lombardi, Géométries élémentaires (vol.1), Presses universitaires de Franche-Comté, , 290 p. (ISBN 978-2-913322-45-5, lire en ligne), chap. 9a (« Le modèle de Beltrami : déplacements et antidéplacements du plan hyperbolique »), p. 230-259.
- René Descartes, Le Livre Premier de La Géométrie de Descartes, , 18 p. (lire en ligne).
- Pierre-Édouard Marchal, Histoire de la Géométrie, , p. 70 et suivantes.
- (en) George Martin, The foundations of geometry and the non-Euclidean plane, New York, Springer, , 447–450 (ISBN 0387906940, lire en ligne).
- (en) « Hyperbolic geometry », sur université de Glasgow (consulté le ).
- Rossana Tazzioli, « Les géométries non euclidiennes : histoire et historiographie », sur Images des mathématiques (consulté le ).
- (en) William Reynolds, « Hyperbolic Geometry on a Hyperboloid », The American Mathematical Monthly, vol. 100, (présentation en ligne).
- (de) Hermann Minkowski, « Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern », Nachrichten der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, , p. 53–111.
- (it) Eugenio Beltrami, « Saggio sulla interpretazione della geometria non euclidea », Gior. Mat., vol. 6, , p. 248–312. Voir également, du même auteur : (it) Opere Matematiche, vol. 1, , 374–405 p. (ISBN 978-1-4181-8434-6 et 1-4181-8434-9) et « Essai d'interprétation de la géométrie noneuclidéenne », Ann. École Norm. Sup. 6, , p. 251–288 (lire en ligne).
- La construction est détaillée dans l'article Métrique de Cayley-Klein.
- (en) Norbert A'Campo et Athanase Papadopoulos, « Notes on hyperbolic geometry », IRMA Lectures in Mathematics and Theoretical Physics, Zürich, strasbourg Master class on Geometry, vol. 18, , p. 1-182 (DOI 10.4171/105).
- (en) Ruben Dashyan, « Représentation de groupes fondamentaux en géométrie hyperbolique », sur Université Pierre-et-Marie-Curie (thèses de doctorat), (consulté le ), section 1.1.
- (en) Abtaham A. Ungar, Gyrovectors : an Approach to Hyperbolic Geometry, t. 4, Morgan & Claypool Publishers, , 182 p. (ISBN 978-159-829-822-2, lire en ligne)
- (en) Jussi Väisälä, « Gromov hyperbolic spaces », Expositiones Mathematicae, vol. 23, no 3, , p. 187–231 (DOI 10.1016/j.exmath.2005.01.010).
- (en) John Stillwell, « Modular Miracles », The American Mathematical Monthly, vol. 108, no 1, , p. 70–76 (ISSN 0002-9890, DOI 10.2307/2695682, JSTOR 2695682)
- Jacques Hadamard, « Les surfaces à courbures opposées et leurs lignes géodésiques », dans Journal de mathématiques pures et appliquées, vol. 4, 1898, p. 27.
- (en) Donald Ornstein et Benjamin Weiss, « Geodesic flows are Bernouillians », Israel Journal of Mathematics, vol. 14, , p. 184.
- (en) Vladimir Arnold et André Avez, Ergodic problems of classical mechanics, Addison-Wesley, coll. « Advanced Book Classics », .
- Pierre Pansu, « Le flot géodésique des variétés riemanniennes à courbure négative », Séminaire Nicolas Bourbaki, Astérisque, vol. 738, , p. 269-298.
- (en) Nándor Balázs et André Voros, « Chaos on the pseudosphere », Physics Report, vol. 143, , p. 109.
- (en) Yves Colin de Verdière, « Hyperbolic geometry in two dimensions and trace formulas », Proceeedings de l'École d'été de physique théorique des Houches (Chaos & Quantum Physics), Marie-Joya Giannoni, André Voros et Jean Zinn-Justin, (ISBN 0-444-89277-X).
- (en) Charles Schmit, « Quantum and classical properties of some billiards on the hyperbolic plane », dans Chaos & Quantum Physics, op. cit.
- « Chapitre 6: Dynamique hyperbolique ».
- On peut citer, par exemple, Chaos on the pseudosphere[54], Hyperbolic geometry in two dimensions and trace formulas[55], ou encore Quantum and classical properties of some billiards on the hyperbolic plane[56] ; on trouvera une synthèse de ces travaux dans le cours de Systèmes dynamiques de l'université Joseph-Fourier[57].
- Jean-Paul Delahaye, « Calculer dans un monde hyperbolique », Pour la science, (lire en ligne)
- (en) Jing-Ling Chen, Libin Fu, Abraham A. Ungar et Xian-Geng Zhao, « Geometric observation for the Bures fidelity between two states of a qubit », Physical Review A, vol. 65, no 2, , p. 3 (lire en ligne, consulté le ).
- (en) Lauren Biron, « Our universe is Flat », symmetrymagazine.org, FermiLab/SLAC, .
- (en) Robert Dicke, Gravitation and the Universe : Jayne Lectures for 1969, American Philosophical Society, (ISBN 978-0-87169-078-4), p. 62.
- Jean-Pierre Luminet, L'Univers chiffonné, Fayard, ; ce terme n'est cependant guère utilisé par la communauté scientifique, qui lui préfère un vocabulaire issu de la topologie (espaces compacts, espaces non simplement connexes, espaces quotients, etc.)
- (en) P. A. R. Ade, N. Aghanim, C. Armitage-Caplan et al., « Planck 2013 results. XXVI. Background geometry and topology of the Universe », Astronomy & Astrophysics, vol. 571, , p. 23 (DOI 10.1051/0004-6361/201321546, arXiv 1303.5086).
- Ainsi, une étude de 2013 de l'observation par le satellite Planck du fond diffus cosmologique, utilise deux espaces hyperboliques[64].
- (en) Jeffrey Weeks, The shape of space, New York, Marcel Dekker, , 2e éd. (ISBN 978-0824707095), p. 219.
- (en) Thomas Hull, « H.P. Lovecraft: a Horror in Higher Dimensions », Math Horizons, vol. 13, no 3, , p. 10–12 (ISSN 1072-4117, lire en ligne, consulté le ).
- Jean-Pierre Petit, Le géométricon, Paris, Belin, , 63 p. (ISBN 2-7011-0372-X).
- (en) « Une version animée de Anges et Démons ».
- (en) « Récit de cette rencontre, avec quelques illustrations ».
- (en) Daina Taimiņa, « Hyperbolic crochet », sur ams.org (consulté le )
- (en) Margaret Wertheim, « The beautiful math of coral », TED, .
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Marcel Berger, Géométrie 2, Paris, Cassini, coll. « Nouvelle bibliothèque mathématique », , 546 p. (ISBN 978-2-84225-146-8), chap. 19 (partie 2) (« Géométrie hyperbolique »)
- Roger Cuppens, Découvrir les géométries non euclidiennes en jouant avec CABRI, t. 1 : Géométrie Hyperbolique, APMEP (no 160), , 128 p. (ISBN 2-912846-37-4, présentation en ligne)
- (en) John Stillwell, Geometry of Surfaces, Springer Verlag, coll. « Universitext », , 236 p. (ISBN 978-0-387-97743-0, lire en ligne)
- (en) Norbert A'Campo et Athanase Papadopoulos, Notes on hyperbolic geometry, Zurich, Société mathématique européenne, coll. « IRMA Lectures in Mathematics and Theoretical Physics » (no 18), , 454 p. (ISBN 978-3-03719-105-7, DOI 10.4171/105, lire en ligne), « Strasbourg Master class on Geometry, p. 1-182 »
- (en) Birger Iversen, Hyperbolic Geometry, vol. 25, London Mathematical Society, Cambridge University Press, coll. « Student Texts », , 298 p. (ISBN 0-521-43528-5, lire en ligne).
- (en) Toshitsune Miyake (trad. du japonais), Modular forms, Berlin/Heidelberg/New York, Springer-Verlag, , 335 p. (ISBN 0-387-50268-8).
Articles connexes[modifier | modifier le code]
- Chaos quantique
- Espace métrique hyperbolique
- Formule des traces de Selberg
- Géométrie non euclidienne
- Géométrie elliptique
- Histoire de la géométrie
- Théorème de Hilbert (géométrie différentielle)
- Variété hyperbolique
- Variété riemannienne
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Rossana Tazzioli, « Les géométries non euclidiennes : histoire et historiographie », sur Images des mathématiques (consulté le ).
- Jos Leys, « Une chambre hyperbolique », sur Images des mathématiques (consulté le ).
- « Promenade non euclidienne », sur ENS Lyon (consulté le ) (conférence donnée par Charles Boubel en 2005).
- David Madore, « Labyrinthes dans le plan hyperbolique », sur madore.org (consulté le ) (avec des commentaires mathématiques en anglais).
- « Géométries non euclidiennes », sur cabri.net (consulté le ), constructions détaillées utilisant le logiciel Cabri Géomètre.
- (en) « Hyperbolic geometry », sur université de Glasgow (consulté le ), site interactif donnant des démonstrations et permettant également des constructions et des calculs dans le modèle du disque de Poincaré.





















