Harmonique sphérique
En mathématiques, les harmoniques sphériques sont des fonctions harmoniques particulières, c'est-à-dire des fonctions dont le laplacien est nul. Les harmoniques sphériques sont particulièrement utiles pour résoudre des problèmes invariants par rotation, car elles sont les vecteurs propres de certains opérateurs liés aux rotations.
Les polynômes harmoniques P(x,y,z) de degré l forment un espace vectoriel de dimension 2 l + 1, et peuvent s'exprimer en coordonnées sphériques (r, θ, φ) comme des combinaisons linéaires des (2 l + 1) fonctions :
- , avec .
Les coordonnées sphériques (r,θ,φ) sont, respectivement, la distance au centre de la sphère, la colatitude et la longitude.
Tout polynôme homogène est entièrement déterminé par sa restriction à la sphère unité S2.
Définition — Les fonctions sur la sphère obtenues par restriction de polynômes homogènes harmoniques sont des harmoniques sphériques.
C'est pourquoi la partie radiale de l'équation de Laplace, différente selon le problème étudié n'apparaît pas ici.
Les harmoniques sphériques sont utilisées en physique mathématique, dès qu'intervient la notion d'orientation (anisotropie) et donc de rotation (groupe de symétrie orthogonal SO(3)) et que le laplacien entre en jeu :
- en acoustique (reconstitution de l'effet d'espace par plusieurs haut-parleurs) ;
- en théorie du potentiel newtonien (électrostatique, mécanique, gravimétrie) ;
- en géophysique (représentation du globe terrestre, météorologie) ;
- en cristallographie pour la texture ;
- en physique quantique (développement d'une fonction d'onde, densité du nuage électronique, description des orbitales atomiques de l'atome d'hydrogène) ;
- en cosmologie (représentation du ciel, en particulier pour l'analyse du fond diffus cosmologique), etc.
Elles sont également utilisées pour des problématiques de rendu 3D, notamment en réalité augmentée afin d'encoder des données d'éclairage ambiant.
Résolution de l'équation de Laplace[modifier | modifier le code]
On cherche les fonctions Yl,m(θ,φ) sous la forme d'un produit de deux fonctions d'une seule variable :
où k est une constante, qui sera fixée ultérieurement par la normalisation. L'équation aux valeurs propres devient une équation différentielle linéaire d'ordre deux pour la fonction Pl,m(cos θ) :

On fait le changement de variable : qui conduit à l'équation différentielle généralisée de Legendre :
Les valeurs propres de cette équation sont indépendantes de m :
Les fonctions propres Pl,m(x) sont les polynômes associés de Legendre. Ils se construisent à partir des polynômes de Legendre Pl(x) qui sont les fonctions propres de l'équation différentielle ordinaire de Legendre, correspondant au cas m = 0 :
On a la formule génératrice d'Olinde Rodrigues :
On construit alors les fonctions propres Pl,m(x) par la formule :
soit explicitement :
Remarque : il suffit en pratique de calculer les fonctions Pl,m(x) pour m ≥ 0, car il existe une relation simple entre Pl,m(x) et Pl, –m(x) :
Expression des harmoniques sphériques[modifier | modifier le code]
On obtient alors l'expression inscrite plus bas. Une manière simple de retenir cette expression est la suivante :
où Pl(x) est le polynôme de Legendre de degré l.
On obtient ensuite :
où
est l'opérateur « d'échelle montante ».
Pour m négatif,
Souvent cette base se note :
toute fonction sur la sphère S2 pourra donc s'écrire :
(en convention de sommation d'Einstein), les coefficients complexes f l,m jouant le rôle de composantes de f dans la base des (on dit parfois coefficients de Fourier généralisés).
En chimie ou en géophysique, il arrive qu'on préfère utiliser les harmoniques sphériques « réelles » et des coefficients de Fourier réels.
Expression mathématique[modifier | modifier le code]
Les harmoniques sphériques formant une base[pourquoi ?][réf. souhaitée] orthogonale sur la sphère unité, toute fonction continue[réf. nécessaire] f(θ,φ) se décompose en[précision nécessaire] une série d'harmoniques sphériques :
où l et m sont des indices entiers, Cm
l est un coefficient constant et souvent en mathématiques prend le nom de coefficient de Fourier généralisé relativement à cette base.
Le développement en harmoniques sphériques est l'équivalent, appliqué aux fonctions angulaires, du développement en séries de Fourier pour les fonctions périodiques.
Ym
l est la partie réelle d'une fonction complexe Ym
l
Ym
l est appelée « fonction associée de Legendre » et est définie par
où i est l'imaginaire et Pm
l est le polynôme associé de Legendre :
On a donc
On a par exemple :
- (Y0
0 est isotrope) ; - ;
- ;
- ;
Les fonctions Ym
l(θ, φ) présentent de plus en plus de symétries au fur et à mesure que l croît (sauf lorsque l = 0, puisque Y0
0 est une fonction constante et décrit donc une sphère).
Polynômes de Legendre[modifier | modifier le code]
Pour les harmoniques circulaires, on utilise des polynômes Pl de la fonction cosinus :
Les polynômes Pl utilisés sont les polynômes de Legendre :
On obtient :
- (fonction isotrope) ;
- ;
- ;
- ;
Harmoniques sphériques normalisées[modifier | modifier le code]
Base orthonormale des harmoniques sphériques[modifier | modifier le code]
Parmi les 2l +1 fonctions, l'habitude a été prise de sélectionner une base orthonormale sur la sphère munie de la mesure
soit le produit scalaire (hermitien en fait) :
Les harmoniques sphériques sont les solutions de l'équation aux valeurs propres[1] :
où l'opérateur laplacien s'écrit en coordonnées sphériques sur la sphère de rayon unité J2 :
Elles sont fonctions propres de l'opérateur :
Celles-ci, une fois normées sur la sphère sont alors notées usuellement Yl,m(θ , φ), où les angles (θ , φ) sont les coordonnées sphériques sur la sphère de rayon unité, et l et m sont deux nombres entiers tels que 0 ≤ l et –l ≤ m ≤ +l
Normalisation[modifier | modifier le code]
Les harmoniques sphériques constituent une base orthonormale de fonctions propres de l'opérateur laplacien sur la sphère de rayon unité S2 au sens où :
Elles sont orthogonales pour le produit scalaire suivant :
Dans cette formule, dΩ(θ, φ) représente l'angle solide élémentaire :
Toute fonction f(θ , φ) suffisamment régulière admet un développement en série :
où les coefficients complexes al,m se calculent par :
Expression des harmoniques sphériques normalisées[modifier | modifier le code]
Les harmoniques sphériques généralisées sont définies sur la sphère S3. La normalisation des harmoniques sphériques conduit à l'expression finale :
Forme « réelle » des harmoniques sphériques[modifier | modifier le code]
Si m ≠ 0 les harmoniques sphériques ont des valeurs complexes. Il est cependant possible, pour une valeur donnée de de définir des combinaisons linéaires des qui soient réelles, tout en constituant toujours une base normalisée sur la sphère unité.
Il suffit pour cela de prendre les combinaisons linéaires suivantes :
Il est facile de vérifier que ces expressions sont bien normalisées à l'unité. Ces relations s'inversent sans difficulté pour donner :
En substituant les expressions précédentes des harmoniques sphériques, on obtient les expressions générales suivantes :
Ces fonctions sont utilisées fréquemment en chimie quantique pour représenter les parties angulaires des différentes orbitales atomiques associées aux différents électrons du cortège électronique des atomes.
Représentations graphiques[modifier | modifier le code]
Représentation sphérique[modifier | modifier le code]
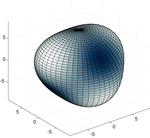
Si l'on utilise la représentation sphérique
alors la surface représentatrice est une sphère bosselée ; les bosses correspondent aux parties où Ym
l est positif, les creux aux parties où Ym
l est négatif.
Lorsque θ et φ décrivent l'intervalle [0 ; 2π[, Ym
l(θ, φ) s'annule selon l cercles :
- m cercles suivant un méridien, une iso-longitude (intersection entre un plan contenant Oz et la sphère) ;
- l – m cercles suivant un parallèle, une iso-latitude (intersection entre un plan parallèle à Oxy et la sphère).
Le paramètre l est appelé le « degré », m est appelé l'« ordre azimutal ». Entre les cercles d'annulation, la fonction est alternativement positive ou négative.
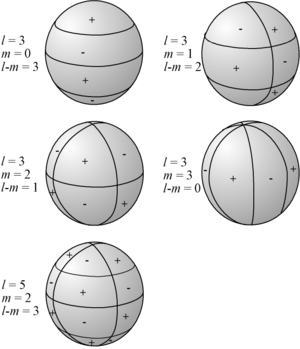
Ci-dessous sont représentées quatre coupes de l'harmonique sphérique Y2
3 :

Comme précédemment, on peut représenter la fonction par la courbe en coordonnées sphériques :
 |

|
les parties en blanc sont positives, en bleu négatives |
Représentation en coupe[modifier | modifier le code]
Les harmoniques sphériques peuvent être représentées de façon plus simple sans les ventres de vibration, en ne gardant que les nœuds, comme le montre le tableau suivant[2]. Ce sont les sphères de la figure du haut, projetées sur un plan vertical. On retrouve sur la dernière ligne les quatre sphères de la première figure ci-dessus où l = 3. Les quatre valeurs de m y varient de 0 à 3 en valeur absolue. Sur la figure ci-après, on distingue les valeurs négatives pour tenir compte de ce que la rotation peut se faire dans un sens ou dans l'autre pour m > 0. Pour montrer la concordance avec les harmoniques, leur plus simple expression est donnée sous chaque sphère.

On reconnaît les nombres quantiques secondaire l, correspondant aux sous-couches s, p, d, f et m, magnétique, de l'atome d'hydrogène. Le nombre quantique principal n n'apparaît pas car les modes radiaux sont différents selon le problème étudié, résonance acoustique, atome d'hydrogène ou autre.
Pour montrer la concordance avec la littérature, l’expression des harmoniques sphériques est donnée sous chaque sphère. Le nombre et la valeur des zéros des polynômes de Legendre associés, non normalisés, donne le nombre de parallèles et leur position sur l’axe vertical. L’exponentielle imaginaire exp(imϕ), de module unité, utilisée habituellement au lieu des sinus et cosinus, donne le nombre de méridiens. Les valeurs de l ≥ 4 ne s’observent que dans les états excités ou les atomes de Rydberg où la valeur habituelle de l est 50 et dont l'orbitale est représentée non par une sphère mais par un anneau[3].
Représentation cartésienne et polaire[modifier | modifier le code]
On peut représenter les harmoniques circulaires de trois manières :
- en coordonnées cartésiennes : y = Yl(θ) ;
- en coordonnées polaires : r = r0 + r1Yl(θ)
avec r1 < r0, utilisé par exemple pour un objet circulaire ; la courbe coupe le cercle de centre O et de rayon r0 lorsque la fonction s'annule ; - en coordonnées polaires : r = |Yl(θ)|2
utilisé par exemple pour les fonctions d'onde en physique quantique.
| Représentation cartésienne | Représentations polaires (tracé manuel) | Représentations polaires (tracé exact) | |
|---|---|---|---|
| Y1 |  |

|

|
| Y2 |  |
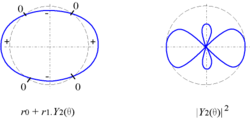
| |
| Y3 |  |
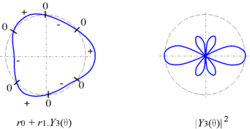
|
Autres harmoniques[modifier | modifier le code]
Harmoniques circulaires[modifier | modifier le code]
Dans le plan, la décomposition s'écrit :
Y0 est une fonction constante, la courbe représentatrice en coordonnées polaires r = Y0(θ) est donc un cercle de rayon r0.
Yl est une fonction invariante par une rotation d'un angle de 1l+1 tour, c'est-à-dire que
on dit que Yl admet une symétrie d'ordre l + 1.
Harmoniques sphériques généralisées[modifier | modifier le code]
Lorsque l'on considère l'orientation d'un objet dans l'espace, il faut faire appel à trois angles ; on utilise en général les angles d'Euler (ψ, θ, φ).
Considérons une fonction continue de l'orientation f(ψ, θ, φ) ; comme précédemment, cette fonction peut être décomposée en harmoniques sphériques généralisées
où Cmn
l est une constante. La fonction Ymn
l s'écrit :
Le polynôme Pmn
l est le polynôme de Legendre généralisé
Quand X décrit l'intervalle [–1 ; 1], cette fonction Pmn
l est soit réelle, soit imaginaire pure. Y00
0(ψ, θ, φ) est la fonction isotrope (symétrie sphérique).
D'après la loi de composition des rotations, on a :
et en particulier
On a de manière générale :
Par exemple pour l = 1 :
| m | n | ||
|---|---|---|---|
| -1 | 0 | +1 | |
| -1 | |||
| 0 | |||
| 1 | |||
Pour l = 2 :
| m | n | ||||
|---|---|---|---|---|---|
| -2 | -1 | 0 | +1 | +2 | |
| -2 | |||||
| -1 | |||||
| 0 | |||||
| 1 | |||||
| 2 | |||||
Notes et références[modifier | modifier le code]
- On a introduit un signe moins pour avoir des valeurs propres positives. En effet, l'opérateur laplacien est un opérateur négatif au sens où, pour toute fonction ϕ lisse à support compact, on a :
Cette égalité se démontre en utilisant la relation Δ = div grad et en intégrant par parties.
- Bernard Schaeffer, Relativités et quanta clarifiés, Publibook, 2007
- Atomes circulaires : propriétés et préparation
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Équation de Laplace
- Atome
- Mécanique quantique
- Atome d'hydrogène
- Orbitale atomique, orbitale moléculaire
- Opérateur laplacien
- Polynôme de Legendre
- Géoïde
- Ambisonie
- Fonction spéciale
Liens externes[modifier | modifier le code]
- Champs géophysiques, C. Vigny, cours de l'École normale supérieure
- La prévision numérique avec le modèle ARPEGE sur le site de Météo-France rubrique Comprendre la météo > Dossiers thématiques > La prévision numérique
- Simulateur d'harmoniques sphériques (programme JavaScript), site de l'École polytechnique (X), Palaiseau, France
- Spherical Harmonic, du site Eric Weisstein's World of Mathematics
- Oscillations propres de la Terre lors d'un séisme, une des applications des harmoniques sphériques (images gif animées) ;
- Représentations 3D de fonctions d'orientation
- Autour des harmoniques sphériques, présentation de différents usages, notamment pour le rendu lumineux 3D
Bibliographie[modifier | modifier le code]
- Isaac Todhunter, An elementary treatise on Laplace's functions, Lame's functions and Bessel's functions, Macmillan and Co, 1875.
- Norman McLeod Ferrers, An elementary treatise on spherical harmonics and subjects connected with them, Macmillan and Co, 1877.
- William Ellwood Byerly, An elementary treatise on Fourier's series and spherical, cylindrical, and ellipsoidal harmonics with applications to problems in mathematical physics, Ginn & Co, 1893.
- René Lagrange, Polynômes et fonctions de Legendre coll. « Mémorial des sciences mathématiques », no 97, Gauthier-Villars, 1939.
- I.S. Gradshteyn et I.M. Ryzhik, Table of Integrals, Series, and Products, éd. Alan Jeffrey and Daniel Zwillinger, Academic Press (6e édition, 2000) (ISBN 0-12-294757-6). Errata sur le site web des éditeurs : [http ://www.mathtable.com/gr/ www.mathtable.com].
- John D. Jackson, Électrodynamique classique — Cours et exercices d'électromagnétisme, Dunod, 2001) (ISBN 2-10-004411-7). Traduction française de la 3e édition du grand classique américain.
- J. L. Basdevant et J. Dalibard, Mécanique quantique [détail des éditions].
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail de l’édition].
- Albert Messiah, Mécanique quantique [détail des éditions].
- H.-J. Bunge, Texture analysis in materials science — Mathematical methods, éd. Butterworths, 1969 (1982 pour la trad. en anglais) : pour les harmoniques sphériques généralisées.
- Yvette Kosmann-Schwarzbach, Groupes et symétries : groupes finis, groupes et algèbres de Lie, représentations, éditions de l'École polytechnique, ; chapitre 7, « Les harmoniques sphériques » (ISBN 978-2-7302-1257-1).









![{\displaystyle -{\frac {\mathrm {d} ~}{\mathrm {d} x}}\left[(1-x^{2}){\frac {\mathrm {d} P_{l,m}(x)}{\mathrm {d} x}}\right]+{\frac {m^{2}}{(1-x^{2})}}P_{l,m}(x)=E_{l,m}P_{l,m}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95fc7809b8cef64eb27f2e3ce35986c51572371f)

![{\displaystyle -{\frac {\mathrm {d} ~}{\mathrm {d} x}}\left[(1-x^{2}){\frac {\mathrm {d} P_{l}(x)}{\mathrm {d} x}}\right]=l(l+1)P_{l}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/391aca5fd64ceeee7a2c65cf31582fdea6957cb8)
![{\displaystyle P_{l}(x)={\frac {1}{2^{l}l!}}{\frac {\mathrm {d} ^{l}~}{\mathrm {d} x^{l}}}\left[x^{2}-1\right]^{l}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20f1d0d9336864b4f6e7fcc347e89cd7637c925d)
![{\displaystyle P_{l,m}(x)=(-1)^{m}\left[1-x^{2}\right]^{m/2}{\frac {\mathrm {d} ^{m}P_{l}(x)}{\mathrm {d} x^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/653d2f04709cf68f1381604d3c9727c41e26a6df)
![{\displaystyle P_{l,m}(x)={\frac {(-1)^{m}}{2^{l}l!}}\left[1-x^{2}\right]^{m/2}{\frac {\mathrm {d} ^{l+m}~}{\mathrm {d} x^{l+m}}}\left[x^{2}-1\right]^{l}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/095bb28b462337fbe6482dab7c4aae6f308f3f6e)










![{\displaystyle P_{l}^{m}(X)={\frac {(-1)^{m}}{2^{l}\cdot l!}}\cdot (1-X^{2})^{m/2}\cdot {\frac {\partial ^{m+l}}{\partial X^{m+l}}}\left[(X^{2}-1)^{l}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f2fe2be1dba98f298556a3cc170d4bacc1417c3)






![{\displaystyle P_{l}(X)={\frac {1}{2^{l}\cdot l!}}\cdot {\frac {d^{l}}{dX^{l}}}\left[(X^{2}-1)^{l}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49956745e091cea7142a548013edecf8dc87b0cc)



























![{\displaystyle P_{l}^{mn}(X)={\frac {(-1)^{l-m}\cdot \mathrm {i} ^{n-m}}{2^{l}\cdot (l-m)!}}\cdot \left[{\frac {(l-m)!(l+n)!}{(l+m)!(l-n)!}}\right]^{1/2}\cdot (1-X)^{-{\frac {n-m}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3f8fc8940f6d1ae19ef01aff033514446175b7a)
![{\displaystyle \cdot (1+X)^{-{\frac {n+m}{2}}}\cdot {\frac {\partial ^{l-n}}{\partial X^{l-n}}}\left[(1-X)^{l-m}(1+X)^{l+m}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcefa72422b71308674cedd4b8d7a70228fa1e16)




















