Sphère de Riemann
En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l'infini, de manière que certaines expressions mathématiques deviennent convergentes et élégantes, du moins dans certains contextes. Déjà envisagée par le mathématicien Carl Friedrich Gauss, elle est baptisée du nom de son élève Bernhard Riemann. Ce plan s'appelle également la droite projective complexe, dénoté .
Introduction[modifier | modifier le code]
La sphère de Riemann, obtenue en ajoutant au plan complexe un point à l'infini, est une variété complexe unidimensionnelle, également appelée une surface de Riemann.
En analyse complexe, la sphère de Riemann permet une expression élégante de la théorie des fonctions méromorphes. La sphère de Riemann est omniprésente en géométrie projective et en géométrie algébrique comme exemple fondamental d'une variété complexe, d'un espace projectif, et d'une variété algébrique. Elle a également une utilité dans d'autres disciplines qui dépendent de l'analyse et de la géométrie, telle que la physique quantique (représentation des états quantiques) et d'autres branches de la physique (théorie des twisteurs par exemple).
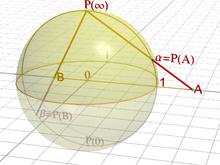
La projection stéréographique, par exemple sur le plan équatorial à partir du pôle Nord, permet de voir que la sphère est homéomorphe au plan complété du point à l'infini . Inversement, on passe du plan à la sphère en ajoutant un pôle, projection du point à l'infini noté . Le plan s'identifie à .
La sphère de Riemann, c'est la sphère usuelle envisagée de ce point de vue, autrement dit la droite projective complexe.
Le théorème d'uniformisation assure que c'est l'unique variété complexe de dimension 1 compacte et simplement connexe.
Remarque[modifier | modifier le code]
Plus généralement, l'espace est homéomorphe à la sphère (sphère unité de l'espace euclidien ) privée d'un point. En effet, est le compactifié d'Alexandrov de .
La droite projective complexe[modifier | modifier le code]
C'est l'ensemble des droites vectorielles de . Une telle droite étant définie par un vecteur non nul, défini à un coefficient de proportionnalité près, on peut la voir comme quotienté par la relation d'équivalence
si et seulement s'il existe un nombre complexe non nul tel que .
On la note , et on note le point associé à . On dit que est un système de coordonnées homogènes du point .
Remarquons aussi que
est une bijection de sur .
De même :
est une bijection de sur .
Ces deux façons d'identifier à privé d'un point sont analogues aux identifications de à la sphère unité privée d'un point à l'aide des projections stéréographiques de pôles Nord et Sud.
Cette remarque permet de donner une bijection explicite entre et . C'est l'application définie par
(ces deux définitions sont compatibles si , grâce à l'équation de la sphère).
Son application réciproque, si on identifie à , et si on représente un point de par des coordonnées homogènes, est
Il est clair que ne dépend pas du choix des coordonnées homogènes. On peut aussi voir comme une application de
On obtient alors la fibration de Hopf.
Homographies[modifier | modifier le code]
On peut faire agir sur la sphère par transformations de Möbius ; la matrice agit sur ainsi :
- si et , on lui associe ;
- si et , on lui associe ;
- si et , on lui associe ;
- si et , on lui associe .
En fait, on obtient ainsi une action à gauche du groupe projectif .
L'application de la sphère de Riemann dans elle-même ainsi définie s'appelle une homographie ; c'est une bijection holomorphe ; inversement, toute bijection holomorphe de la sphère de Riemann est une
homographie.



















![{\displaystyle [z,t]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c474e7a02bedac61014390da300bff8fca6c521)

![{\displaystyle \phi _{1}:z\mapsto [z,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0479a737a50ee39898917aa7b088cbf730851a02)
![{\displaystyle \mathbb {P} ^{1}(\mathbb {C} )\setminus [1,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1608e22f417a091f035340d1b50e004ba4e7d4be)
![{\displaystyle \phi _{2}:z\mapsto [1,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9752fc1605d4e9277f22a11c449e99c2923e2cc)
![{\displaystyle \mathbb {P} ^{1}(\mathbb {C} )\setminus [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc146ec167e92c75306741708edc959f031a7047)



![{\displaystyle g(X,Y,Z)=[X+iY,1-Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fff0f807ac37fcfd0d892d6e41a7417d6fc969d7)

![{\displaystyle g(X,Y,Z)=[1+Z,X-iY]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52295d60eae27e0a8650ba383cdec2d21087596c)




















