Transformation conforme

Une France conforme

... et anticonforme

En mathématiques, et plus précisément en géométrie et en analyse complexe, une transformation conforme est une bijection qui conserve localement les angles, c'est-à-dire qui se comporte au voisinage de chaque point où elle est définie presque comme une similitude.

Dans le plan, les transformations conformes qui conservent les angles orientés ont une telle utilité qu'il est fréquent qu'elles soient les seules baptisées du terme de conformes. Elles se confondent alors avec les bijections holomorphes. Les transformations conformes indirectes sont, dans ce cas, appelées transformations anticonformes.

On rencontre les transformations conformes en géométrie différentielle, dans la résolution de l'équation de Poisson, en mécanique des fluides pour modéliser des écoulements, et en cartographie.

La notion de transformation conforme se généralise à des espaces de dimension supérieure à 2, mais elle y perd un peu de sa diversité.

Cas du plan

Une transformation conforme dans le plan, f est une transformation d'un domaine du plan dans un plan, cette transformation conservant (localement) les angles entre deux courbes orientées, c'est-à-dire que si deux courbes $C_1$ et $C_2$ se coupent en A, et que leurs vecteurs tangents en A (dans le sens de l'orientation) forment un angle $\alpha$, les vecteurs tangents en f(A) aux deux courbes images $f(C_1)$ et $f(C_2)$ forment également l'angle $\alpha$. Autrement dit, f est localement une similitude directe.

Les transformations qui inversent les angles sont dites anticonformes ; ce sont les composées des précédentes par les réflexions.

Définition par l'analyse complexe

Si une transformation fait correspondre un point $M=f(m)$ à un point m, elle peut s'interpréter dans le plan complexe comme une relation $Z = f(z)$ entre les affixes de ces deux points (en gardant la même notation pour les deux fonctions).

On peut prouver qu'une fonction holomorphe conserve les angles orientés en tout point où sa dérivée est non nulle et que réciproquement, une fonction différentiable de différentielle non nulle et conservant les angles orientés est nécessairement holomorphe de dérivée non nulle.

De plus, on peut prouver qu'une fonction holomorphe bijective sur un ouvert U possède une dérivée qui ne s'annule jamais sur U. Ce qui conduit à l'identification suivante :

Soient $U$ et $V$ deux ouverts de $\mathbb{C}$. $f : U \rightarrow V$ est une transformation conforme de $U$ sur $V$ si $f$ est holomorphe sur $U$ et est une bijection de $U$ sur $V$.

Cette identification a été utilisée, en particulier pour calculer simplement des écoulements autour d'un profil d'aile, en utilisant une transformation qui fait passer d'un cercle au profil voulu. Cela est possible grâce au théorème de l'application conforme, garantissant l'existence d'une telle transformation pour des formes assez générales.

De la même manière, $f$ est une transformation anticonforme si c'est la conjuguée d'une transformation conforme.

Exemples holomorphes

Pavage du plan par l'image d'une horloge. Cette figure est utilisée dans toutes les transformations de cet article.

L'image d'une horloge après une similitude.

Aux coordonnées cartésiennes (x,y) d'un point du plan, on préfère la notation $x+i\,y\in\mathbb{C}$ du plan complexe. En effet, on peut non seulement ajouter les vecteurs (ou points) du plan mais également les multiplier. La multiplication par un nombre réel r correspond à une homothétie, celle par un nombre unitaire $e^{i\theta}$ à une rotation d'angle θ et celle par un nombre complexe quelconque $z=r\,e^{i\theta}$ correspond à une similitude. Les similitudes sont clairement des transformations conformes.

Une fonction holomorphe (ou analytique) est localement une similitude $f(z)=a\,(z-z_0)+b+o(z-z_0)$ avec $a=f'(z_0)$ la dérivée et $b=f(z_0)$ la valeur de f en z₀. La dérivée est le facteur de zoom de cette transformation. Elle est donc une transformation conforme là où sa dérivée ne s'annule pas. Aux zéros de la dérivée, l'application n'est pas conforme et ressemble localement à un monôme:

Les monômes $z\mapsto z^k$ sont les fonctions holomorphes les plus simples, après les similitudes qui sont de dérivée constante. Un problème pour les représenter est qu'une fonction holomorphe n'est en général pas injective: Pour le monôme $z^k$ par exemple k points différents sont envoyés sur la même valeur à part 0 où la dérivée est nulle et où l'application n'est pas conforme car les angles en 0 sont multipliés par k. On dit qu'il est de multiplicité k.

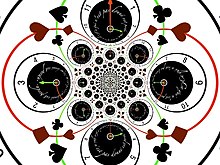
Si on considère le plan pavé par l'image d'une horloge, sa mise au carré sera :

Une horloge au carré. Remarquez le double recouvrement de chaque point.

Le disque central est envoyé sur lui-même mais chaque point (sauf zéro) est recouvert deux fois, ce qui rend l'image illisible. Par exemple +1 (à 3h) et -1 (à 9h) sont envoyés sur +1 (à droite de l'image au milieu), +i (midi) et -i (6h) sont envoyés sur -1 (9h).

Une somme de monômes est un polynôme. Son monôme de plus haut degré détermine son degré : chaque point complexe est atteint le même nombre de fois (en comptant les multiplicités).

Pour avoir une application injective, on peut se restreindre par exemple soit au demi-plan de partie réelle positive, soit à l'autre demi-plan de partie réelle négative.

Le demi-plan de partie réelle négative au carré.

Le demi-plan de partie réelle positive au carré.

En prenant de la distance, le même effet opère sur le plan entier.

• 

  Le demi-plan de partie réelle négative au carré.

• 

  Horloge au carré: application conforme mais non injective.

• 

  Le demi-plan de partie réelle positive au carré.

Image réciproque

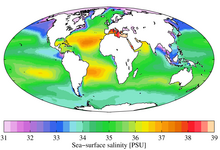
On peut également considérer non pas l'image directe par une application, mais plutôt l'image réciproque (aussi parfois appelée le tiré en arrière, traduction de pullback):

On place alors l'image non pas dans l'espace de départ mais plutôt dans l'espace d'arrivée et on colore le point z par la couleur du pixel f(z).

Le tiré en arrière par $z\mapsto z^2$.

Remarquez la duplication : les points z et -z sont envoyés tous deux sur la même image z².

Un polynôme de degré 4, on repère les zéros de sa dérivée. Les zéros simples n'ont rien de spécial.

Le tiré en arrière par $z\mapsto z^3$.

De même, le monôme d'ordre k envoie k points à la même image.

On comprend de nombreuses informations concernant l'application conforme en visualisant le tiré en arrière d'une image. Comme le facteur de zoom de l'image directe est la dérivée de la fonction, c'est donc son inverse en ce qui concerne l'image réciproque. On remarque en particulier les zéros de la dérivée où le facteur de zoom devient donc infini. On remarque également quand la dérivée est réelle positive, là où l'image ne subit qu'une dilatation, et quand la dérivée est réelle négative, là où l'image est "la tête en bas".

Inversion, pôles

L'anti-inversion $z\mapsto 1/z$.

Repliement du demi-plan de Poincaré dans le disque unité par la transformation conforme $z \mapsto \frac{1+iz}{z+i}$ puis déploiement par la transformation réciproque $z \mapsto \frac{1-iz}{z-i}$

L'anti-inversion (détail).

L' inversion $z\mapsto \frac{1}{\overline{z}}$ est une transformation anticonforme, sa conjuguée, appelée parfois anti-inversion, est la transformation $z\mapsto 1/z$. C'est une transformation conforme possédant un pôle simple en zéro. Cette transformation échange l'intérieur et l'exterieur du disque unité.

C'est un cas particulier de transformation de Möbius $z \mapsto \frac{az+b}{cz+d}$ avec a, b, c et d quatre complexes tels que $ad - bc \neq 0$ et elle envoie cercles et droites sur cercles et droites. En particulier les horizontales et verticales deviennent des cercles passant par zéro.

C'est parmi ces fonctions homographiques complexes que l'on trouve les transformations conformes transformant des demi-plans en disques

Logarithme et exponentielle

L'application exponentielle $z\mapsto e^z$. Remarquez les invariances par homothétie et rotation qui correspondent à les invariances par translations horizontales, resp. verticales du réseau.

Le logarithme $z\mapsto \log(z)$. Remarquez que le disque unité déroulé se répète verticalement.

Une application très importante en analyse complexe et en cartographie est la transformation de coordonnées cartésiennes (x,y) en coordonnées polaires (r,θ). Cette transformation est réalisée par le couple de fonctions logarithme/exponentielle réciproques l'une de l'autre ($\log(\exp(z))=z$). En effet, $\log(r\,e^{i\theta})=\log(r)+i\theta$ transforme (r,θ) en (x=log(r), y=θ) et $\exp(x+i\,y)=\exp(x)\,e^{i\, y}$ transforme (x,y) en (r=exp(x),θ=y). En images, le logarithme déroule les cercles centrés en l'origine en droites verticales et des rayons en droites horizontales. L'exponentielle au contraire, enroule les droites verticales en cercles concentriques et les droites horizontales en rayons passant par l'origine. Remarquez que le logarithme va vers l'infini en zéro mais beaucoup plus lentement que l'inversion.

Transformation conforme dans un espace affine euclidien quelconque

Les transformations conformes sont les difféomorphismes de classe C¹ d'un ouvert U dans un ouvert V dont la jacobienne est une similitude. Elles conserve localement les angles, mais pas nécessairement leur orientation.

Les seules transformations conformes définies sur l'espace euclidien tout entier sont les similitudes.

Liouville a démontré que, contrairement au cas du plan, en dimension n ≥ 3, les seules transformations conformes de classe C⁴ définies sur un ouvert U sont les produits d'inversions et de similitudes, c'est-à-dire les transformations conservant l'ensemble des hypersphères et des hyperplans.

Applications pratiques

Mécanique des fluides

Au début de l'aérodynamique la transformation conforme a fourni, sous l'hypothèse d'un écoulement irrotationnel d'un fluide supposé incompressible et parfait (voir Mécanique des fluides), une méthode élégante de calcul de l'écoulement bi-dimensionnel autour d'un profil d'aile et de sa portance. Certaines transformations bien choisies permettent en effet de transformer un cercle en une courbe ressemblant à un profil d'aile et en déduire la portance d'une aile de grand allongement.

La première application de cette technique correspond à ce qu'on appelle la transformation de Joukovsky :

$Z = \frac {1} {2} \left(z + \frac {a^2} {z}\right)$

Cette équation simple conduit à un profil qui présente des inconvénients, en particulier parce que le bord de fuite d'un tel profil possède un point de rebroussement, ce qui met en cause sa réalisation pratique.

Cartographie

Certaines projections cartographiques sont conformes. Citons par exemple la projection stéréographique (plane), la projection de Mercator et sa généralisation (cylindriques), et la projection de Lambert (conique).

Articles connexes

• Symétrie conforme
• Théorème de l'application conforme