Variété (géométrie)

En mathématiques, et plus particulièrement en géométrie, la notion de variété peut être appréhendée intuitivement comme la généralisation de la classification qui établit qu'une courbe est une variété de dimension 1 et une surface est une variété de dimension 2. Une variété de dimension n, où n désigne un entier naturel, est un espace topologique localement euclidien, c'est-à-dire dans lequel tout point appartient à une région qui s'apparente à un tel espace[1].

On peut approcher les variétés de deux façons :
- En les construisant par recollement d'autres espaces simples, comme les enfants s'amusent à construire avec du papier des tétraèdres, des cubes et autres polyèdres en dessinant la figure d'un patron sur une feuille, en découpant convenablement les bords, en pliant et en recollant ou comme on construit un vêtement en cousant ensemble des morceaux de tissus. Par exemple, les mathématiciens obtiennent un cercle en repliant un segment sur lui-même, un cylindre ou un cône en repliant une bande plane sur elle-même. Un autre exemple classique est le ruban de Möbius illustré ci-contre (en toute rigueur, c'est un exemple de variété à bord). Il est également possible de rajouter des anses à une sphère ;
- En leur appliquant une trame dont la métrique dépend de la position. Par exemple, pour les coordonnées sphériques terrestres (altitude, latitude et longitude), un changement de longitude correspond à une distance qui dépend de la latitude (un degré de longitude correspond à une distance plus longue à l'équateur qu'ailleurs). On parlera dans ce cas de variété riemannienne.
Il est difficile de dire qui le premier a étudié les courbes ou les surfaces en tant qu'objets mathématiques abstraits. Gauss disposait de la notion de surface abstraite, mais la notion générale de variété en dimension quelconque est due à Bernhard Riemann. Les variétés se sont imposées comme le cadre naturel de nombreux problèmes de mathématiques et de physique, permettant de travailler dans un cadre plus vaste que celui des espaces vectoriels. On donne parfois à ces derniers le nom d’espaces plats ou d’espaces euclidiens pour les distinguer des espaces courbes que sont les variétés.
La topologie algébrique cherche à classer les variétés (mais aussi des objets plus généraux) en en déterminant des invariants, c'est-à-dire des objets mathématiques — qui peuvent être des nombres réels — associés à chaque variété et qui en caractérisent la topologie. Certaines variétés sont munies de structures plus fortes : il est du ressort de la topologie différentielle, puis de la géométrie différentielle, de la géométrie riemannienne et de la géométrie symplectique de les étudier et de les classifier. Ces domaines sont encore aujourd'hui l'objet de nombreux travaux de recherches.
Les variétés constituent à la fois un cadre et un sujet d'étude communs pour les chercheurs en mathématiques et en physique. Elles se sont avérées les bons outils de travail pour formaliser la relativité générale d'Einstein et ont fortement servi dans la physique post-newtonienne, dont la théorie des cordes, la théorie des membranes... Les variétés sont devenues tout aussi utiles (voire indispensables) dans des travaux récents de mécanique classique. Les variétés sont à l'origine d'une hypothèse sérieuse pour expliquer les étonnantes capacités de généralisation des algorithmes d'apprentissage profond.
Introduction[modifier | modifier le code]
Les difficultés qui existent pour représenter sur un plan une surface sphérique comme la Terre sont un bon moyen d'appréhender la géométrie différentielle. C'est aussi la raison pour laquelle le vocabulaire de cette branche des mathématiques emprunte beaucoup à celui de la cartographie.
Les cartes[modifier | modifier le code]
On se déplace sur la sphère terrestre en utilisant des cartes géographiques planes, rassemblées en un atlas. Au bord d'une carte figure l'information nécessaire pour y « recoller mentalement » la carte suivante. Pour opérer ce recollement, une certaine redondance dans l'information est nécessaire : ainsi la carte de l'Europe et celle de l'Asie peuvent toutes deux contenir Moscou. De manière similaire, il est possible de décrire une variété en utilisant une collection de cartes, réunies en un atlas mathématique, indiquant comment passer d'une carte à l'autre. Le globe terrestre fournit un exemple typique de variété, puisqu'il peut être représenté par une collection de cartes géographiques.

Une carte est une portion de la variété analogue à une portion d'espace vectoriel ; les changements de cartes indiquent comment ces portions de variétés se raccordent entre elles. Ainsi, pour décrire un cercle il est possible de prendre comme cartes deux arcs qui se chevauchent ; le changement de cartes constitue une information sur le recollement au niveau de la zone de chevauchement.
Il n'est généralement pas possible de décrire une variété à l'aide d'une seule carte, parce que la structure globale de la variété est différente de la structure simple de l'espace modèle. Par exemple, aucune carte « plate » ne peut décrire convenablement la Terre entière. Les variétés apparaissent comme des espaces topologiques et leurs topologies sont uniquement déterminées par la donnée de leurs atlas respectifs.
Suivant la nature des applications de changement de cartes, la variété possède une structure plus ou moins forte : variété topologique, variété différentielle, variété localement plate par exemple. Pour une variété topologique, la donnée d'un atlas équivaut simplement à la donnée d'une topologie dont les ouverts suffisamment petits s'identifient à l'espace plat. Pour les structures plus fines citées, l'introduction de cartes est indispensable pour les définir.
La dimension et la topologie[modifier | modifier le code]

La première notion attachée à une variété est sa dimension. Elle désigne le nombre de paramètres indépendants qu'il faut se fixer pour positionner localement un point sur la variété.
- Les courbes sont des variétés de dimension un puisque l'abscisse curviligne par exemple suffit à décrire la position.
- Sur une surface, il faut deux coordonnées : ainsi sur une sphère il faudra préciser latitude et longitude, comme c'est le cas pour indiquer l'emplacement d'une ville sur le globe terrestre.
- Il existe de nombreuses variétés de dimension supérieure à deux, qu'il est difficile de représenter graphiquement. Elles ne peuvent en effet se représenter dans notre espace environnant, qui est de dimension trois (largeur, longueur, hauteur).
Toutes les variétés de même dimension n — ou n-variétés — ont la même topologie locale. Par définition, une petite portion de ces variétés ressemble toujours à un espace vectoriel réel de dimension n. Ainsi une petite portion de courbe est l'analogue courbe d'une droite, une petite portion de surface l'analogue courbe d'un plan, et ainsi de suite.
En revanche, les variétés se distinguent par leur aspect global. Par exemple sur la figure ci-contre, la variété rouge est formée de deux morceaux bornés (deux cercles), et il est visiblement impossible de déformer continûment celle-ci pour obtenir une des trois autres courbes.
Autre exemple, une sphère et un tore ne se ressemblent pas topologiquement. Tout cercle tracé sur une sphère la sépare en au moins deux morceaux disjoints ; cependant, il existe de nombreux cercles tracés sur un tore qui ne le séparent pas en morceaux disjoints. Plus généralement, la topologie peut se compliquer par la présence de « trous », d'« anses », etc.
Variété abstraite et sous-variété[modifier | modifier le code]

De nombreux sous-ensembles particuliers du plan et de l'espace de dimension 3 peuvent être naturellement munis d'une structure de variétés : le cercle, le cylindre, la sphère, le ruban de Möbius, etc. ; on les appelle sous-variétés ou variétés plongées. Il existe en outre une notion de variété abstraite, qui sont construites sans qu'on les considère comme une sous-variété. L'exemple le plus simple est l'espace projectif de dimension n : c'est simplement l'ensemble de toutes les droites passant par l'origine dans un espace vectoriel de dimension n + 1. Un autre exemple de variété abstraite est la bouteille de Klein, représentée ci-contre de façon imparfaite. Pour mieux l'appréhender visuellement, il faut imaginer un artisan verrier prenant une bouteille ordinaire, perçant son fond, allongeant le goulot, le courbant et le faisant traverser le flanc de la bouteille pour le raccorder au fond (chose importante, le goulot passe à travers le flanc « comme par magie », sans y faire de trou). La bouteille de Klein peut être décrite par un système de cartes et de coordonnées représenté ici par un maillage de méridiens et de parallèles, elle est donc de dimension 2.
Le théorème de plongement de Whitney montre que toute variété abstraite de dimension n peut être réalisée comme sous-variété d'un espace de dimension suffisamment grande, à savoir de dimension 2n. Ainsi la bouteille de Klein (de dimension 2) ne peut être plongée dans l'espace à trois dimensions, mais forme une sous-variété de l'espace à quatre dimensions.
L'introduction des variétés abstraites peut paraître superfétatoire au premier abord. Cependant, il y a des avantages à s'affranchir de la considération de l'« espace ambiant », celui dans lequel serait plongée la variété. En particulier, de nombreux modes de construction de nouvelles variétés à partir de variétés déjà définies, à l'exemple des quotients et des recollements topologiques (voir plus loin), ne font intervenir que les variétés elles-mêmes, et (surtout) pas l'espace qui pourrait éventuellement les entourer. Quand bien même en théorie il est possible de les réaliser comme sous-variétés d'un espace vectoriel, il ne serait pas judicieux de le faire en pratique, et cela ne présenterait aucun intérêt.
Histoire[modifier | modifier le code]
On se contente ici d'une esquisse du mouvement historique qui a conduit à l'émergence du concept général de variété ; pour une histoire plus détaillée de l'évolution et de l'application de ce concept dans diverses branches des mathématiques (ex : géométrie riemannienne, géométrie symplectique), on renvoie aux articles dédiés.
Premiers résultats de géométrie intrinsèque[modifier | modifier le code]
Il est difficile de dater quand précisément les questions de géométrie intrinsèque intéressèrent particulièrement les géomètres. Les Grecs posaient des problèmes invoquant les propriétés métriques d'un ensemble de points définis et positionnés dans le plan et dans l'espace. L'intérêt était explicitement porté sur le point de vue extrinsèque.
On attribue traditionnellement à Euler la découverte en 1752 d'une propriété des polyèdres convexes[2]. En notant respectivement S, A et F les nombres de sommets, arêtes et faces, il démontre l'identité S – A + F = 2, identité connue aujourd'hui sous le nom de relation d'Euler. Le résultat est d'autant plus surprenant qu'il ne fait intervenir ni les longueurs, ni les aires. Il est en fait encore valable pour les nombres de sommets, faces et arêtes d'une triangulation de la sphère. C'est le premier exemple de calcul de la caractéristique d'Euler d'une surface.
En 1813, L'Huilier remarque que la formule d'Euler est modifiée pour un polyèdre non-convexe, par exemple ayant la forme d'un solide avec des trous (comme le tore, qui a un trou). Elle devient S – A + F = 2 – 2g, en notant g le nombre de trous[3]. C'est là le premier calcul d'un invariant topologique permettant de classer les surfaces de l'espace. Cependant, le point de vue reste extrinsèque car les trous sont vus de l'extérieur. Comment une fourmi marchant sur une chambre à air peut-elle se représenter le trou ?
L'un des plus grands mathématiciens de son temps, Carl Friedrich Gauss, en s'intéressant à la géométrie des surfaces, établit un « résultat remarquable » (le theorema egregium) :
« la courbure de Gauss d'une surface de l'espace ne dépend pas de la façon dont celle-ci est plongée dans l'espace ambiant[4]. »
La formule de Gauss-Bonnet, pressentie par Gauss et démontrée par Pierre-Ossian Bonnet en 1848, donnera l'expression de la caractéristique d'Euler en termes de courbure, témoignant de l'imbrication des considérations géométriques et topologiques.
De nouveaux espaces aux propriétés étranges[modifier | modifier le code]
La géométrie non euclidienne naît de l'impossibilité de démontrer le cinquième postulat d'Euclide. On peut en trouver la première trace dans une tentative de démonstration par l'absurde de Saccheri en 1733[5]. Gauss serait le premier à avoir compris la possibilité qu'il existe des géométries alternatives à celles d'Euclide[6]. De telles géométries seront effectivement développées par Lobatchevski et Bolyai.
Le ruban de Möbius est introduit presque simultanément en 1858 par deux mathématiciens allemands August Ferdinand Möbius et Johann Benedict Listing. Il s'agit d'une surface de l'espace, facile à réaliser avec une bande de papier, et qui n'a qu'une seule face, une seule arête. C'est le premier exemple de surface non orientable.
Les variétés de Riemann[modifier | modifier le code]

Bernhard Riemann fut le premier à étendre de façon systématique la notion de surface à des objets de dimension plus grande, qu'il baptisa Mannigfaltigkeit[7],[8]. Cette terminologie a d'ailleurs donné le terme anglais manyfold ou manifold. Il en donne une description intuitive, une variété de dimension n étant un empilement continu de variétés de dimension n-1. Notons que cette description intuitive n'est en fait valable que localement, c'est-à-dire au voisinage de chaque point de la variété, dans l'acception moderne de variété. Riemann utilise ce concept pour décrire l'ensemble des valeurs d'une variable soumise à certaines contraintes, comme l'ensemble des paramètres décrivant la position d'une figure dans l'espace.
Les variétés connaissent rapidement beaucoup d'applications, pour l'étude du prolongement analytique et des variétés abéliennes en analyse complexe, pour l'étude des flots différentiables avec l'application de premier retour de Poincaré, pour la définition des mécaniques hamiltonienne et lagrangienne en physique. En 1904, en étudiant les variétés de dimension trois, Henri Poincaré soulève un des problèmes les plus célèbres de la théorie des variétés, connu sous le nom de conjecture de Poincaré, et dont la preuve par Grigori Perelman a été validée en .
La notion de variété, bien qu'ayant trouvé une popularité certaine, restait floue. Hermann Weyl donna en 1912[9] une définition intrinsèque des variétés différentielles. Les publications des années 1930, notamment à l'occasion de la preuve du théorème de plongement par Hassler Whitney[10], établirent les résultats fondateurs de la théorie et donnèrent une popularité au nouvel objet[11].
Applications des variétés[modifier | modifier le code]
Les applications des variétés en mathématiques sont nombreuses. Contentons-nous de quelques exemples. Pour commencer, l'analyse réelle classique et l'analyse fonctionnelle ont vu leur terrain d'investigation s'étendre logiquement des espaces vectoriels topologiques aux variétés. De même, les processus stochastiques à l'exemple du mouvement brownien s'étendent des espaces réels de dimension finie aux variétés. Aussi les variétés apparaissent-elles de manière épisodique en statistiques. Plus encore, des ensembles intéressants ont à la fois une structure algébrique et une structure de variété compatibles. Ainsi l'ensemble des rotations dans un espace à 3 dimensions forme une 3-variété et un groupe. La théorie des groupes de Lie étudie ces variétés à propriétés algébriques. La théorie des espaces homogènes étudie leurs actions transitives.
L'espace des configurations d'un système physique[modifier | modifier le code]
En physique, l'étude des systèmes mécaniques fait entrer en ligne de compte l'ensemble des positions que le système est a priori susceptible d'adopter, appelé espace des configurations. Celui-ci possède souvent une structure de variété ; cependant, il peut ne pas avoir la structure plus rigide de variété différentielle : des singularités peuvent apparaître. La dimension de cette variété s'interprète comme le nombre de paramètres physiques indépendants qui permettent de décrire l'état du système.
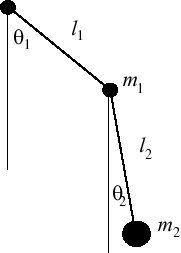
Ainsi dans le cas du pendule double dans le plan, l'état du système est complètement décrit par la donnée de deux angles. On pourrait donc être tenté de dire que l'espace des configurations est [0, 2π] × [0, 2π]. Mais en réalité, l'état décrit par le couple d'angles (0, 0) est le même que celui décrit par (2π, 2π). Donc il s'agit d'identifier les côtés opposés du carré [0, 2π] × [0, 2π] deux à deux. On obtient ainsi un tore. De manière équivalente, un angle est paramétré de manière bijective par un point du cercle S1, donc un couple d'angles est paramétré de manière bijective par un point de l'espace S1 × S1, qui définit aussi le tore. Le premier angle permet de désigner un point sur le cercle rouge, le second un point sur le cercle rose. Le point du tore désigné par les deux angles s'obtient à l'intersection de deux cercles de coordonnées (en gris).
 |
 |
Les lois de la physique s'interprètent alors comme des équations différentielles écrites sur la variété, et peuvent être traitées dans le cadre de la mécanique lagrangienne. Une reformulation, qui se présente comme un changement de coordonnées locales, débouche sur la mécanique hamiltonienne. Celle-ci utilise comme soubassement mathématique les variétés symplectiques, modélisant l'espace des phases.
L'espace des phases ne se résume pas à l'espace des configurations. La raison en est que la dynamique hamiltonienne fait intervenir des dérivées secondes. De même que dans l'étude des équations différentielles ordinaires d'ordre 2, on ajoute la vitesse à la position pour obtenir des équations ordinaires d'ordre 1. L'opération cependant est plus délicate ici et nécessite une bonne maîtrise des structures impliquées : elle fait appel à la théorie des fibrés vectoriels.
Variétés et physique théorique[modifier | modifier le code]
La physique théorique contemporaine utilise abondamment les variétés différentielles ; mentionnons par exemple :
- L'espace temps de la relativité générale, qui est un continuum courbé à 4 dimensions (espace+temps), modélisé par une variété à quatre dimensions munie de ce qu'on appelle une pseudo-métrique lorentzienne de signature (–, +, +, +).
- Les théories de champs de jauge dans l'espace-temps, modélisé comme précédemment par une variété lorentzienne à quatre dimensions (pas nécessairement courbe), utilisent pour leurs parts la notion enrichie d'espace fibré différentiel. Il s'agit encore d'une variété différentielle, mais de dimension plus grande que celle de l'espace-temps, qui joue ici le rôle d'espace de base du fibré. On considère plus précisément un fibré principal, dont la fibre s'identifie au groupe de structure qui est un groupe de Lie précisant la symétrie (« invariance de jauge ») de la théorie. Un champ de jauge A y apparaît comme une connexion d'Ehresmann, et la forme de Yang-Mills associée F = dA s'interprète comme la courbure associée à cette connexion. (Ces outils se définissent plus généralement dans la théorie des fibrés principaux.) Ont ainsi été démontrées pertinentes pour le monde réel :
- La théorie de jauge classique U(1), qui s'identifie à la théorie électromagnétique de Maxwell. C'est une théorie abélienne. Cette théorie admet des extensions non abéliennes intéressantes appelées théories de Yang-Mills, basées sur les groupes non abéliens SU(n).
- Après quantification, deux des théories de Yang-Mills constituent l'actuel « modèle standard » de la physique des particules :
- Le modèle électro-faible de Glashow, Salam et Weinberg est basé sur le groupe U(1) × SU(2) et décrit de façon unifiée l'électromagnétisme et l'interaction nucléaire faible.
- La chromodynamique quantique est basée sur le groupe SU(3) et décrit l'interaction nucléaire forte entre les quarks et les gluons.
- La théorie du tout exceptionnellement simple, soutenue par Garrett Lisi, et basée sur E8, le plus grand groupe de Lie simple exceptionnel. Cette théorie n'est pas à ce jour validée par l'expérience, mais constitue actuellement la seule[réf. nécessaire] tentative (invalidée rapidement par plusieurs publications, comme précisé sur la page de Garrett Lisi) de poursuite du développement de la physique théorique à partir de la seule utilisation d'une théorie de jauge. On peut noter que la correspondance AdS/CFT est une tentative des plus sérieuses de théorie du tout dont la définition non-perturbative repose sur une théorie de jauge.
Un exemple détaillé : le cercle[modifier | modifier le code]

Après la droite réelle, l'exemple le plus simple de variété est le cercle. Il existe essentiellement deux manières de l'introduire : on pense ici à un cercle tracé dans le plan euclidien ℝ2, dont les coordonnées usuelles sont notées x et y. Par une similitude, on se ramène à un cercle de centre (0, 0) et de rayon 1. Un tel cercle est implicitement défini par l'équation x2 + y2 = 1.
Un premier atlas[modifier | modifier le code]
Localement, le cercle ressemble à une ligne, qui est à une dimension. En d'autres termes, une seule coordonnée suffit pour décrire un petit arc de cercle. Considérons par exemple la partie supérieure du cercle, pour laquelle la coordonnée y est positive (partie jaune sur la Figure 1). N'importe quel point de cette partie peut être décrit par la coordonnée x. Il y a donc un homéomorphisme χhaut, qui relie la partie jaune du cercle à l'intervalle ouvert ]−1, 1[ en représentant chaque point du cercle par sa première coordonnée :
Une telle fonction est appelée une carte. De manière similaire, il existe des cartes pour les parties inférieure (rouge), gauche (bleue) et droite (verte) du cercle. Ensemble, elles recouvrent la totalité du cercle et on dit que les quatre cartes forment un atlas de ce cercle.
Les deux cartes supérieure et gauche se recouvrent. Leur intersection est située dans le quart de cercle où les coordonnées x et y sont respectivement négative et positive. La carte χhaut réalise une bijection qui à (x, y) associe x, partant de la zone de recouvrement vers l'intervalle ]–1, 0[. La carte χgauche par laquelle (x, y) donne y associe à cette même zone de recouvrement l'intervalle ]0, 1[. Ainsi, il est possible de créer une fonction T de l'intervalle ]–1, 0[ vers ]0, 1[ :
Une telle fonction est appelée une application de changement de carte ou de transition. Elle permet de passer du système de coordonnées x choisi pour la première carte au système de coordonnées y choisi pour la seconde.
Un autre atlas[modifier | modifier le code]

Les cartes supérieure, inférieure, gauche et droite montrent que le cercle est une variété, mais ne constituent pas le seul atlas envisageable. Les cartes n'ont pas besoin d'être des projections géométriques, et le nombre de cartes est presque arbitraire.
Voici un autre exemple de description du cercle. Prenons pour point de base le point de coordonnées (-1, 0) et traçons les différentes droites issues de ce point ; la droite de pente s recoupe le cercle en un point unique. La correspondance entre la pente de la droite et les coordonnées du point d'intersection est dans un sens :
et dans l'autre sens :
Cette première carte décrit tous les points du cercle hors le point de base.
Pour fabriquer la deuxième carte on effectue une symétrie en prenant comme point de base (+1, 0) et comme pente -t avec :
Ces deux cartes fournissent un second atlas du cercle, avec pour application de changement de carte
Noter que chaque carte omet un point unique, soit (–1,0) pour s ou (+1,0) pour t, donc aucune des cartes seule ne peut décrire complètement le cercle.
Bilan[modifier | modifier le code]
On vérifierait que les deux atlas présentés sont compatibles, c'est-à-dire qu'en regroupant les quatre cartes du premier et les deux cartes du second, on obtient un nouvel atlas, encore plus redondant. Chacun des deux atlas, ainsi que l'atlas global, définissent donc la même notion de repérage par carte et coordonnées locales, c'est-à-dire la même structure de variété. On montrerait encore, à l'aide du théorème des fonctions implicites que la donnée de l'équation permet aussi de créer des systèmes de cartes locales adaptées.
On voit donc à travers ces exemples la flexibilité amenée par l'utilisation de cartes : on dispose d'un choix infini d'atlas compatibles sur le cercle, qu'il faut prendre adaptés à la géométrie du problème étudié. Cependant, à l'aide d'arguments topologiques on peut montrer qu'une carte seule ne peut jamais couvrir l'ensemble du cercle.
En dimension supérieure[modifier | modifier le code]
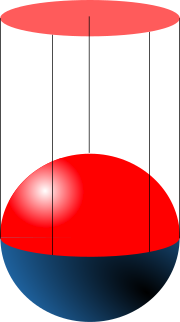

La méthode envisagée pour le premier atlas du cercle peut aisément être généralisée pour des sphères de dimension supérieure. La n-sphère Sn est une généralisation de l'idée de cercle (1-sphère) et de sphère (2-sphère) à des dimensions supérieures. Une n-sphère Sn peut être construite en considérant 2(n + 1) cartes correspondant aux deux projections sur chacun des n + 1 hyperplans de coordonnées, et les applications de changement de cartes. Une carte pour un tel atlas est illustrée ci-contre dans le cas de la 2-sphère.
Dans le cas de la 2-sphère, c'est-à-dire du globe usuel, le deuxième atlas envisagé pour le cercle admet aussi une généralisation : c'est un atlas constitué des deux projections stéréographiques depuis les pôles nord et sud respectivement.
Définition des variétés[modifier | modifier le code]
Définition des variétés topologiques[modifier | modifier le code]
La définition précise des variétés nécessite l'usage d'un vocabulaire relativement spécialisé. Si on veut entrer dans les détails, une variété topologique de dimension n, ou n-variété, est un espace topologique séparé, localement homéomorphe à un espace vectoriel réel de dimension n. On la supposera en outre généralement à base dénombrable d'ouverts. Ces hypothèses et d'autres sont évoquées dans l'article « Variété topologique » et motivées de façon détaillée dans sa version anglophone.

Dans l'exemple du cercle, il est possible de trouver des homéomorphismes locaux (les cartes) avec la droite réelle. En revanche sur la lemniscate de Bernoulli de la figure ci-contre, il n'existe pas de carte locale au voisinage du point double. En effet en prenant un voisinage en forme de disque, si petit soit-il, de ce point, le morceau de lemniscate est une croix ce qui en topologie est distinct d'un morceau de droite.
Les variétés peuvent être un seul morceau, ce qui se formalise par la notion de connexité, ou constituées de plusieurs morceaux portant le nom de composantes connexes.
Au moins dans le cas connexe, il est possible de ne pas fixer a priori de dimension dans la définition d'une variété. En effet dans ce cas le théorème d'invariance de la dimension de Brouwer (1912) montre que les homéomorphismes locaux définis sur les ouverts de l'espace topologique aboutissent tous à des espaces vectoriels d'une même dimension[12]. On retrouve dans cette dimension commune la dimension de la variété.
Structures différentielles[modifier | modifier le code]
Sur une variété topologique, il n'est pas possible de définir une notion de fonction différentiable. De ce fait, les méthodes fécondes et théorèmes importants issus du calcul différentiel sont inapplicables, alors même que certains — le théorème des fonctions implicites par exemple — prennent tout leur sens par une interprétation géométrique et sont, au fond, des énoncés destinés à l'étude des variétés.
Il est donc nécessaire d'introduire quelques restrictions à la notion de variété si on souhaite disposer de ce vaste champ de méthodes, notamment du concept de vecteur tangent ou de celui de sous-ensemble de mesure nulle. Pour essayer de donner une analogie, une simple variété topologique de dimension 1 est une courbe absolument quelconque ; sa structure très souple ne permet pas de distinguer un cercle d'une courbe fractale, par exemple un flocon de Koch. Au contraire, la ressemblance entre une variété différentielle de dimension 1 et un cercle est bien plus rigide.
Techniquement, la définition la plus usuellement rencontrée consiste à ajouter une information supplémentaire à la structure topologique de la variété ; on introduira un sous-ensemble de l'ensemble de tous les homéomorphismes entre un ouvert de la variété et un ouvert de ℝn qu'on appellera un atlas, les homéomorphismes appartenant à la variété étant appelés des cartes. On exige d'abord que les cartes couvrent toute la variété. Pour pouvoir ensuite définir des fonctions p fois différentiables sur la variété, il est nécessaire d'exiger une condition technique supplémentaire : que les applications de « changement de cartes » (obtenues par composition d'une carte et de la réciproque d'une autre) soient elles-mêmes p fois continûment différentiables. On parle alors de variété de classe Cp, ou de variété analytique si on requiert la ℝ-analyticité des changements de cartes.
Autres structures additionnelles[modifier | modifier le code]
De même que spécifier une structure différentielle particularise une variété topologique, et offre une nouvelle boîte à outils à l'utilisateur, on peut énumérer d'autres définitions particularisant cette fois le concept de variété différentielle.
Ainsi ceux de :
- Variété riemannienne : une variété riemannienne est une variété munie d'un métrique riemannienne, ce qui permet non seulement le calcul des distances mais aussi l'analyse fonctionnelle sur les variétés. En physique, on emploie plus couramment tenseur métrique au lieu de métrique riemannienne. Une variété pseudo-riemannienne dispose d'un tenseur métrique qui n'est pas défini positif. Ces variétés sont à la base de la relativité générale ;
- Variété symplectique : une variété symplectique est une variété utilisée pour représenter les espaces de phase en mécanique classique. Elle est munie d'une forme différentielle qui définit l'opérateur crochet de Poisson ;
- Groupe de Lie : un groupe de Lie est une variété différentielle disposant d'une structure de groupe compatible avec sa structure de variété.
Construction de variétés[modifier | modifier le code]
Une même variété peut être construite de différentes manières, chacune mettant en valeur un aspect différent de la variété, menant par conséquent à un point de vue légèrement différent. Pour construire effectivement une variété, il faut disposer d'un matériau de base, d'une (ou d'un ensemble de) variétés. Parmi les modes de construction les plus connus, citons :
- Le produit cartésien, permettant d'accéder facilement à des variétés de dimensions supérieures ;
- Le recollement de variétés, permettant en pratique de complexifier la topologie des variétés tout en préservant leur dimension ;
- Le quotient de variétés, autre moyen de complexifier la topologie, mais avec éventuellement une perte de dimensions.
Variété abstraite construite par recollement[modifier | modifier le code]
Dans les exemples proposés jusqu'ici, une partie d'un espace vectoriel était munie d'un atlas lui conférant une structure de variété. Il est possible également de considérer des variétés abstraites, c'est-à-dire définies à partir d'une collection d'applications formant un atlas abstrait. La variété est alors construite par assemblage, les ouverts de cartes servant de briques de base pour de telles constructions, et l'atlas donnant les instructions nécessaires aux raccordements. Du fait qu'aucun espace extérieur n'est impliqué, cette construction mène à une vue intrinsèque de la variété.
Construction du cercle et de l'hypersphère par recollement[modifier | modifier le code]
Un bon exemple de construction intrinsèque est celle du cercle. En se donnant deux droites disjointes, l'une étant décrite par la coordonnée réelle s, et l'autre par la coordonnée t, on assemble les deux en collant (en identifiant) le point de coordonnée t de la deuxième sur le point de coordonnée s = 1⁄t de la première (le point t = 0 de la seconde droite n'est identifié avec aucun point de la première droite ; de même pour le point s = 0 de la première droite). Cette construction fournit un espace topologique, muni de cartes, qui peut facilement être identifié au cercle plongé dans le plan usuel, muni du deuxième atlas proposé dans l'exemple ci-dessus.
La n-sphère Sn est une généralisation de l'idée de cercle (1-sphère) et de sphère (2-sphere) à des dimensions supérieures. Une n-sphère Sn peut être construite en assemblant deux copies de ℝn. L'application de transition est alors définie par
qui généralise l'exemple du cercle donné précédemment.
Identifier des points d'une variété[modifier | modifier le code]
La construction est la même en général : la variété est construite en partant d'un atlas abstrait, défini par des ouverts de ℝn et des applications de transition compatibles entre elles. Un point de la variété est une classe d'équivalence (opération de collage) de points qui sont associés par les cartes de transition. Cette construction par recollement conduit à une variété qui n'est pas incluse dans un espace de référence, mais définie par elle-même. Ce point de vue abstrait est purement intrinsèque.
L'action d'assembler ces points en un seul, correspond à la notion d'espace quotient. Néanmoins des difficultés topologiques surgissent et il n'y a pas de raison a priori pour qu'un tel espace quotient soit une variété. C'est ce qui explique qu'on introduise des variantes de la notion de variétés, notamment orbifolds, CW-complexes, qui généralisent la notion de variété, ou variétés à singularités coniques, qui généralisent plus spécifiquement la notion de variété différentielle.
L'opération de passage au quotient est une des méthodes fondamentales de construction de variétés, qui dépasse la question du recollement. Une méthode classique d'identification des points est l'utilisation d'une action de groupe sur la variété. Deux points sont identifiés si l'un d'eux est envoyé sur l'autre par un élément du groupe. Sous certaines conditions topologiques, on peut affirmer que l'espace quotient forme une variété. C'est exactement le mode de construction des tores, des espaces projectifs réels, ou des espaces projectifs complexes (à partir d'un plan, d'une n-sphère et d'un espace vectoriel complexe respectivement). Cette construction connue sous le nom de variété quotient recouvre en partie les concepts de revêtement et d'espace homogène. Elle n'est pas davantage développée ici.
Définition par équations[modifier | modifier le code]

Un autre mode de définition classique des variétés est la donnée d'une équation, ou d'un système d'équations. Un des exemples les plus simples est celui du cercle unité, courbe du plan défini par l'équation par exemple. La même équation dans l'espace à trois dimensions définit une surface de révolution, à savoir le cylindre. Plus généralement, dans l'espace , en se donnant une équation de la forme , et sous certaines conditions sur la fonction F (vecteur gradient jamais nul), on obtient une variété de dimension n – 1, ou hypersurface. Cet ensemble de valeurs s'appelle un ensemble de niveau. Le géographe a l'habitude de les manipuler en cartographiant une région montagneuse : sur les cartes, des courbes sont tracées indiquant des points d'égale altitude. Les cartes obtenues sont appelées cartes topographiques.
En algèbre linéaire, on définit un sous-espace vectoriel de codimension p à l'aide de p formes linéaires. Ces formes linéaires forment une famille linéairement indépendante du dual, et le sous-espace est le lieu des points d'annulation de ces p formes. De même, il est possible de considérer un système (non linéaire en général) de p équations à n inconnues. La situation locale revêt alors une analogie forte avec la résolution d'un système d'équations linéaires. Sous de bonnes hypothèses (à savoir, l'indépendance linéaire des vecteurs gradients), l'ensemble des solutions du système forme une variété de dimension n-p. L'outil de base pour étudier ces questions est le théorème des fonctions implicites, avec les corollaires associés.
Si la condition donnée est locale, c'est que la vérification qu'un ensemble est une sous-variété est locale. De fait, le discours se généralise au monde des variétés. Sous de bonnes hypothèses, un ensemble de fonctions sur une variété permettent d'en définir des sous-variétés. Cette technique est couramment utilisée en pratique.
Enfin, ce mode de définition est le mode de définition général pour les variétés algébriques.
Variété à bord[modifier | modifier le code]

La définition des variétés interdit la présence de « bord » comme dans le cas d'un disque plein par exemple. Il est possible de définir cependant une notion de « variété à bord », en acceptant des cartes ayant pour domaine des ouverts de ℝn – 1×ℝ+. Le bord d'une telle variété à bord sera une variété de dimension n – 1. Ainsi une sphère pleine, ou boule, est une 3-variété à bord, dont le bord est une 2-variété, la sphère.
Assemblage par les bords[modifier | modifier le code]
Deux variétés à bords peuvent être assemblées en les collant le long d'un bord. Si ceci est fait correctement, le résultat est aussi une variété. De la même manière, deux composantes du bord d'une même variété peuvent être collées. De nouveau, l'assemblage est défini par un homéomorphisme permettant d'identifier les points d'un bord à ceux de l'autre.
Un cylindre fini peut être construit en partant d'un carré [0,1] × [0, 1] et en cousant ensemble deux côtés opposés. Les deux cercles qui forment le bord de la figure obtenue peuvent ensuite être repliés l'un sur l'autre pour former un tore ou une bouteille de Klein.
L'opération de topologie amusante la plus célèbre est certainement celle qui consiste à recoller deux bords d'un carré, mais en renversant l'orientation ; on n'obtient plus alors un cylindre mais un anneau de Möbius, aussi appelé bande de Möbius ou ruban de Möbius, qui est l'exemple standard pour illustrer la notion de variété non orientable. Il s'agit d'une variété à bord dont le bord est un cercle. En recollant un disque le long de ce cercle, on obtient un plan projectif réel. Si le ruban de Möbius peut être visualisé dans ℝ3, le recollement ne peut pas être effectué dans l'espace tridimensionnel : un quatrième degré de liberté est indispensable.
Produit cartésien[modifier | modifier le code]
De même que le produit cartésien d'espaces vectoriels est un espace vectoriel, le produit cartésien de variétés est aussi une variété. Sa topologie est la topologie produit et un produit cartésien de cartes est par convention une carte pour le produit. Ainsi, un atlas de ce qu'on appelle la variété produit peut être construit à l'aide d'un atlas de chaque facteurs. Si ces atlas définissent une structure différentielle sur les facteurs, l'atlas correspondant définit une structure différentielle sur la variété produit. Ceci est vrai pour toute autre structure définie à l'aide des facteurs. La dimension de la variété produit est la somme des dimensions de ses facteurs. Les produits cartésiens peuvent être utilisés pour construire des tores et des cylindres finis, par exemple : S1 × S1 et S1 × [0, 1], respectivement.
Toutes les variétés ne peuvent pas être écrites à l'aide d'un produit, mais certaines peuvent s'écrire comme une réunion disjointe d'un ensemble de sous-variétés qui a localement la structure d'un produit ; elles portent le nom de feuilletages. Par exemple, l'hypersphère de dimension trois admet un feuilletage remarquable en cercles (disjoints), connu sous le nom de fibration de Hopf, du nom du topologue Heinz Hopf.
Approfondissements[modifier | modifier le code]
Structures connexes[modifier | modifier le code]
Pour mettre en œuvre la géométrie sur des variétés, il est souvent requis d'ajouter des structures additionnelles à ces espaces, tels que ceux vus plus haut pour les variétés différentielles. Il existe de nombreuses autres possibilités, dépendant du type de géométrie qu'on cherche à introduire :
- Variété analytique : la définition est analogue à celle de variété différentielle, mais on impose que les applications de changement de cartes soient des difféomorphismes analytiques. Toute variété différentiable admet une structure de variété analytique.
- Variété complexe : une variété holomorphe est une variété construite sur ℂn à l'aide de fonctions de transitions holomorphes sur des recouvrements de cartes. Ces variétés sont les objets de base pour l'étude de la géométrie complexe. Une variété à une dimension complexe est appelée surface de Riemann. (Noter qu'une variété complexe à n dimensions a 2 n dimensions en tant que variété différentielle réelle.)
- Variété de Banach ou variété banachique et Variété de Fréchet : pour permettre l'extension aux dimensions infinies, on peut considérer des variétés de Banach qui soient localement homéomorphes à des espaces de Banach. De même, les variétés de Fréchet sont localement homéomorphes à des espaces de Fréchet.
- Variété à singularités coniques : incluent les variétés différentielles, les variétés différentielles à bord, les cônes, les polyèdres, aussi bien en tant que surfaces qu'en tant que solides.
- Orbifold : Un orbifold est la généralisation des variétés pour certains types de singularité dans la topologie.
- Variété algébrique et schéma : une variété algébrique est construite par assemblage de variétés algébriques affines, qui sont des ensembles de zéros de polynômes construits sur des corps commutatifs. La domestication des recollements à opérer n'est plus basée sur la régularité des changements de cartes, mais en décrivant lesquelles des fonctions définies localement sur la variété méritent d'être considérées comme régulières ; la notion de faisceau se substitue alors à celle d'atlas comme outil technique pour la définition. Les schémas sont de même construits à partir de schémas affines, qui sont eux-mêmes une généralisation des variétés algébriques affines.
- CW-complexe : un CW-complexe est un espace topologique formé d'objets de différentes dimensions par recollements successifs. Pour cette raison, ce n'est généralement pas une variété. Cependant, il est d'un intérêt central en topologie algébrique : il permet de coder la topologie et d'en donner une approche essentiellement combinatoire. Toute variété topologique admet une décomposition en CW-complexe.
Classification des variétés[modifier | modifier le code]
Un problème central en mathématiques concerne la possibilité d'identifier deux objets ensemblistement distincts mais dont les propriétés sont semblables. En ce sens, deux variétés sont identifiées lorsqu'il existe une bijection entre elles qui soit compatible avec la topologie. Une telle bijection est appelée homéomorphisme. Par exemple, le cercle considéré comme sous-variété du plan, ou le cercle abstrait construit par recollement, s'ils sont ensemblistement différents, sont homéomorphes. Du point de vue de la topologie, la surface d'un ballon de foot ou d'un ballon de rugby est la même. Les différences entre ces deux objets sont de nature métrique.
Le problème général devient : quand peut-on identifier deux variétés topologiques à homéomorphisme près ? Deux variétés différentielles à difféomorphisme près ?
Les premiers résultats dans ce sens, très partiels, concernent la classification des surfaces, aujourd'hui bien connue. Cette classification repose sur la caractéristique d'Euler, et le genre. Cette caractéristique se généralise aisément aux dimensions supérieures, grâce à la notion de faces de dimension supérieure. Ce qui importe est alors la configuration des triangulations des variétés, et la caractéristique d'Euler ne code qu'une partie des informations sur ces triangulations. Pour avoir accès aux informations restantes, il faut abandonner l'idée d'invariants numériques, et étudier des invariants algébriques associés aux triangulations : c'est la naissance des méthodes homologiques et cohomologiques, suivant les idées de Poincaré sur l'homologie singulière. Des méthodes homotopiques, dont le niveau élémentaire est l'étude de la simple connexité, apportent aussi des réponses.
Ces méthodes s'adaptent, dans un certain sens, en considérant d'autres cohomologies, aux types de variété plus rigides : par exemple, la cohomologie de De Rham pour l'étude des variétés différentielles. Les invariants obtenus ne forment en général pas des systèmes complets d'invariants : c'est-à-dire que deux variétés peuvent topologiquement se distinguer, alors qu'elles sont cohomologiquement semblables, au sens où leurs groupes de cohomologie sont identiques.

Un autre problème intéressant de classification provient des déformations des sous-variétés plongées : on ne s'autorise alors plus n'importe quelle déformation, mais seulement certaines qui respectent la topologie de l'espace sous-jacent, les homotopies, ou bien les isotopies, suivant le problème considéré. À nouveau, des méthodes cohomologiques et homotopiques sont utiles. On obtient des classifications plus fines, où le nœud trèfle, et le cercle, confondues homéomorphiquement, sont cette fois bien distincts. La théorie des nœuds notamment s'intéresse au plongement d'un cercle dans l'espace à trois dimensions, ou dans la sphère tridimensionnelle.
Toujours plus en avant, la théorie des nœuds a permis de donner la construction effective des variétés de dimension 3. En quelques mots, toute variété compacte de dimension 3 s'obtient en effectuant un nombre fini d'opérations sur la sphère tridimensionnelle au voisinage d'un nombre fini de nœuds disjoints. Pour chaque nœud, il s'agit d'en retirer un voisinage, un tore plein, et de le recoller différemment. La topologie de la variété ne dépend que de la classe d'homotopie des données de recollement, qui sont des homéomorphismes du tore. L'argumentation est détaillée dans l'article 3-variété, ou l'ouvrage de Dale Rolfsen. L'utilisation d'un unique nœud trivial donne naissance à un ensemble de variétés compactes de dimension 3, appelées espaces lenticulaires.
Discussions autour des variétés[modifier | modifier le code]
Lors d'études plus approfondies sur la topologie des variétés sont rencontrées des discussions récurrentes portant sur la dimension des variétés ou la rigidité des structures :
- Les petites dimensions offrent peu de degrés de liberté. De fait, il n'est pas rare que des structures pourtant différentes en grandes dimensions coïncident en dimensions 1, 2, 3, éventuellement 4, 5. Cependant, l'excès de contraintes peut rendre l'approche difficile. À cet égard, citons le problème posé par Poincaré concernant la caractérisation topologique d'une sphère de dimension n. La preuve en dimension n ≥ 5 a valu la médaille Fields à Stephen Smale en 1966, la preuve en dimension 4 a valu la médaille Fields à Michael Freedman en 1986, la preuve en dimension 3 a valu la médaille Fields à Grigori Perelman en 2006 (mais celui-ci l'a refusée) ;
- La seconde thématique concerne la souplesse ou la rigidité des structures additionnelles sur les variétés.
Notes et références[modifier | modifier le code]
- (en) John J. O'Connor et Edmund F. Robertson, « Manifold », sur MacTutor, université de St Andrews.
- La paternité pourrait en être cependant attribuée à Descartes, voir l'article théorème de Descartes-Euler.
- M. Lhuilier, « Mémoire sur la polyédrométrie […] », Annales de Gergonne, vol. 3, 1812-1813, p. 169–189 (lire en ligne [archive du ]).
- C.F. Gauss, Disquisitiones generales circa superficies curvas, 1827.
- (la) Saccheri, Euclides ab omni naevo vindicatus, 1733.
- (en) John J. O'Connor et Edmund F. Robertson, « Gauss biography », sur MacTutor, université de St Andrews..
- (de) B. Riemann, Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse, thèse de doctorat de 1851.
- (de) B. Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen, soutenance d'habilitation de 1854.
- (en) H. Weyl, The concept of a Riemann surface, Addison Wesley, éd. de 1955.
- (en) H. Whitney, Differentiable Manifolds, Annals of Mathematics 37, 1936, p. 645-680.
- Voir par exemple (en) Morris W. Hirsch, Differential Topology [détail des éditions], p. 2.
- (de) L. E. J. Brouwer, Zur Invarianz des n-dimensionalen Gebiets, Mathematische Annalen 72, 1912, p. 55-56.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Courbe (variété de dimension 1)
- Surface (variété de dimension 2)
- 3-variété (variété de dimension 3)
- Topologie algébrique
- Géométrie différentielle
- Orientation d'une variété
- Relativité générale
- Chirurgie (topologie)
- Colimite
- Topologie en basses dimensions
Lien externe[modifier | modifier le code]
(en) John J. O'Connor et Edmund F. Robertson, « History Topics: Geometry and Topology Index », sur MacTutor, université de St Andrews.
Bibliographie[modifier | modifier le code]
- Jean-Pierre Bourguignon, Espaces courbes [détail des éditions]Introduction non technique au sujet.
Aspects techniques[modifier | modifier le code]
- Boris Doubrovine (de), Anatoli Fomenko et Sergueï Novikov, Géométrie contemporaine - Méthodes et applications, [détail des éditions] (Première partie : géométrie des surfaces, des groupes de transformations et des champs)Une introduction très pédagogique à la géométrie, avec des applications à la physique, écrite par des spécialistes russes. L'approche étant plutôt intuitive, cet ouvrage est accessible à partir du premier cycle universitaire pour un bon étudiant motivé.
- Marcel Berger et Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions]Ouvrage issu d'un cours de magistère de mathématiques.
- (en) Michael Spivak, (A Comprehensive Introduction to) Differential Geometry [détail des éditions]Traité de référence en cinq volumes.
- (en) Dale Rolfsen, Knots and Links [détail des éditions]
- (en) John Milnor, Topology from the Differentiable Viewpoint [détail des éditions]
- Jacques Lafontaine, Introduction aux variétés différentielles [détail des éditions]Ouvrage élémentaire pour les étudiants de master.
Ouvrages de mathématiques pour physiciens théoriciens[modifier | modifier le code]
- (en) Theodore Frankel, The Geometry of Physics - An introduction, Cambridge University Press, 2004, 2e éd. révisée et illustrée (ISBN 978-0-52153927-2)
- (en) Mikio Nakahara, Geometry, Topology and Physics, Institute of Physics Publishing, 2003, 2e éd. illustrée (ISBN 978-0-75030606-5)
- (en) Charles Nash et Siddhartha Sen, Topology and Geometry for Physicists, Academic Press, 1983 (ISBN 978-0-12514080-5)
- (en) Yvonne Choquet-Bruhat et Cécile DeWitt-Morette, Analysis, Manifolds and Physics - Part I: Basics, North-Holland, 1989 (ISBN 978-0-44486017-0)
Aspects historiques[modifier | modifier le code]
- Luciano Boi, Le problème mathématique de l'espace - Une quête de l'intelligible, Springer, 1995 (ISBN 978-3-54058922-8)Une histoire philosophique du concept mathématique d'espace, de la géométrie euclidienne au développement des géométries modernes non euclidiennes. Niveau premier cycle universitaire minimum.
- (en) Marvin Jay Greenberg, Euclidean and non-Euclidean geometries – Development and history, Freeman, 4e éd. 2007 (ISBN 978-0-71679948-1)Un livre de mathématiques qui retrace l'histoire et le développement des géométries non euclidiennes, essentiellement à deux dimensions (géométries de Gauss, Bolai et Lobachevsky). Accessible à l'« honnête homme » cultivé.
- (en) Max Jammer, Concepts of Space - The History of Theories of Space in Physics, Dover, 3e éd. 1993 (ISBN 978-0-48627119-4)Une histoire érudite du concept d'espace, depuis l'Antiquité jusqu'à nos jours. Niveau premier cycle universitaire.











