Surface minimale
En mathématiques et en physique, une surface minimale est une surface minimisant son aire tout en réalisant une contrainte : un ensemble de points, ou le bord de la surface, est d'avance déterminé. Si un cerceau est retiré d'une bassine d'eau savonneuse, un disque de liquide reste fixé. Un souffle dessus déforme légèrement le disque en une calotte sphérique. Si l'étude fait appel à la mécanique des fluides, le traitement mathématique utilise le langage des surfaces minimales. Usuellement, une définition oblige de préciser le contexte : quel est l'espace ambiant ? quel sens donner à la notion d'aire ? à la minimisation ?
En géométrie différentielle élémentaire, une surface minimale est une surface fermée et bornée d'un espace affine réel euclidien de dimension 3 à bord régulier minimisant l'aire totale à contour fixé. La définition se généralise en géométrie différentielle : une surface minimale dans une variété riemannienne donnée est le plongement d'une variété compacte à bord minimisant le volume riemannien à bord fixé.
Intuitivement, une surface minimale est une surface dont l'aire ou le volume ne peut qu'augmenter lorsqu'on lui applique une perturbation suffisamment petite. Les surfaces minimales forment donc l'analogue en dimension supérieure des géodésiques (courbes dont la longueur ne peut qu'augmenter sous l'effet d'une perturbation assez petite et assez localisée).

Décrire les surfaces minimales n'est pas un problème mathématique simple. La première approche est d'effectuer un calcul des variations sur l'aire ou le volume riemannien vu comme une fonctionnelle d'énergie. Cette méthode permet d'en décrire les points critiques : il s'agit des surfaces dont la courbure moyenne est nulle, ou des sous-variétés dont la courbure moyenne est nulle. Cette propriété est parfois présentée comme une définition des surfaces minimales. Les deux définitions (point critique ou véritable minimum) ne sont pas équivalentes.
Certaines surfaces minimales peuvent être matérialisées par des bulles de savon s'appuyant sur un contour, car le film de savon tend à minimiser son énergie, donc sa superficie. Elles sont utilisées justement en ingénierie pour minimiser la surface de contact et donc par exemple les pertes d'énergie.
Une question connexe est celle de la surface d'aire minimale englobant un volume donné. Elle est traitée dans l'article « Isopérimétrie ».
Histoire[modifier | modifier le code]
En 1744, Leonhard Euler posait et résolvait le premier problème de surface minimale : trouver, entre toutes les surfaces passant par deux cercles parallèles, celle dont la surface était la plus petite. Il découvrit ainsi la caténoïde. En 1755, Lagrange, alors âgé de 19 ans, énonce l'équation d'Euler-Lagrange s'appliquant à une surface minimale s'appuyant sur un contour fermé (voir ci-dessous pour une preuve actualisée). En 1776, Meusnier déduit de l'équation différentielle de Lagrange que les courbures principales doivent être opposées, ce qui se traduit par une courbure moyenne nulle. Il découvre par la même occasion l'hélicoïde.

Depuis lors, il est établi que les surfaces minimales de l'espace euclidien s'appuyant sur un contour donné ont une courbure moyenne nulle. Cette propriété traduit l'aspect local de la surface : pour qu'une déformation légère ne puisse qu'augmenter la surface, il faut qu'elle soit de type selle, comme l'illustre le schéma ci-contre. Lorsqu'on déforme une surface convexe (à gauche), donc de courbure moyenne non nulle, toutes les lignes de cette surface s'allongent ou rétrécissent en même temps (en rouge). En revanche, lorsqu'on déforme une surface de type selle, certaines de ces lignes de surface s'allongent alors que d'autres rétrécissent, selon la direction, illustrant le fait que la surface elle-même est de courbure moyenne nulle.
En 1866, Weierstrass démontre qu'une solution à l'équation d'Euler-Lagrange vérifie les équations de Cauchy-Riemann : une telle solution est donc une fonction holomorphe. En 1873, le physicien belge Joseph Plateau généralise une observation expérimentale faite à l'aide de films de savons : pour tout contour donné homéomorphe à un cercle, il existe une surface minimale, donc une solution à l'équation d'Euler-Lagrange. On appela par la suite « problème de Plateau » le fait de trouver cette solution.
Une recherche particulièrement active en géométrie différentielle se concentre sur les surfaces minimales depuis les années 1960[1]. Avant 1980, seuls six types de surfaces minimales de l'espace euclidien étaient connues : le plan, la caténoïde, l'hélicoïde, la surface d'Enneper et les deux types de surfaces de Scherk. Mais en 1981, William Meeks (de), se basant sur des travaux antérieurs de Celso José da Costa, publia une nouvelle famille[2], et bientôt suivirent des dizaines d'autres[3]. Ce sont les progrès de l'informatique qui rendirent possibles ces découvertes en multipliant la puissance de calcul des ordinateurs.
Il existe aujourd'hui plus d'une centaine de familles de surfaces minimales complètes. De nombreuses questions restent encore ouvertes notamment en dimension supérieure. La recherche actuelle vise à minimiser la courbure moyenne par une étude menée sur les flots[4].
Exemples[modifier | modifier le code]
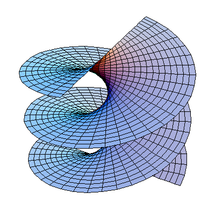

- La caténoïde ;
- la gyroïde ;
- l'hélicoïde ;
- la surface minimale de Bour (en) ;
- la surface minimale de Catalan ;
- la surface de Costa ;
- la surface d'Enneper ;
- la surface de Henneberg (en) ;
- la surface d'Hoffman ;
- les surfaces de Scherk ;
- les surfaces minimales de Schwarz (en) ;
- la trinoïde.
La caténoïde et l'hélicoïde ont la propriété remarquable de pouvoir être déformées continûment l'une en l'autre, la déformation étant localement en tout point une isométrie. De plus, toutes les surfaces intermédiaires sont des surfaces minimales. Pour cela, on prend la paramétrisation suivante, où t est le paramètre de déformation, variant de 0 pour la caténoïde à pour l'hélicoïde et (u,v) sont les paramètres décrivant la surface intermédiaire à t donné :
La sphère, qui possède une courbure moyenne constante non nulle, n'est pas une surface minimale au sens restrictif du terme. Elle vérifie cependant une autre propriété de minimisation : elle est la surface d'aire minimale enfermant un volume donné (voir l'article « Théorème isopérimétrique »).
Propriétés mathématiques[modifier | modifier le code]
Équation aux dérivées partielles[modifier | modifier le code]
Une surface lisse de R3 peut localement après changement de coordonnées (euclidiennes) être représentée comme le graphe d'une fonction réelle à deux variables u et v. Plus précisément, la surface devient l'ensemble des points de coordonnées :
et en utilisant les notations et , l'équation locale d'Euler-Lagrange se réécrit :
Cette équation donne une relation non évidente entre les dérivées partielles de f aux premier et second ordre : c'est un exemple d'équations aux dérivées partielles.
Exemples : La seule famille de solutions de la forme en est l'hélicoïde. La seule famille de solution de la forme est une surface de Scherk.
- Même si cela peut paraître contre-intuitif, il n'y a pas unicité de solution au problème de Plateau. En d'autres termes, il n'existe pas toujours qu'une unique surface minimale s'appuyant sur un contour donné. Voici quelques éléments sur le nombre de surfaces minimales par contour :
- Si le contour est une courbe plane, il ne borde qu'une surface minimale. De même s'il se projette simplement sur un plan suivant une courbe convexe (Rado, 1932) ;
- Un contour dont la courbure totale est inférieure à ne peut border qu'une surface minimale du type du disque ;
- Une courbe analytique ne peut border qu'un nombre fini de surfaces d'aire minimale.
Application de la théorie de Morse[modifier | modifier le code]
La théorie de Morse se relève assez efficace pour compter les points critiques ; elle est célèbre pour avoir donné les inégalités de Morse qui permettent d'obtenir des estimations pour le nombre de points critiques d'une fonction définie sur un espace compact de dimension finie. Les surfaces de courbure nulle se présentent comme les points critiques de l'aire ou du volume. Il est tentant d'appliquer la théorie de Morse : cependant, les variations sur les surfaces impliquent nécessairement une étude en dimension infinie. La compacité ne peut plus être invoquée pour des raisons topologiques fondamentales[5].
Toutefois, une théorie analogue est réalisable et fournit l'identité :
où n est le nombre de surfaces minimales distinctes, et les des entiers, nombres caractéristiques associés à chaque surface minimale.
Application à la physique[modifier | modifier le code]
Capillarité[modifier | modifier le code]

Dans certains cas, on peut matérialiser une surface minimale par un film de savon. En effet, un film de savon tend à minimiser son énergie potentielle ce qui revient à diminuer sa surface. Plus précisément, il obéit à l'équation de Laplace-Young : , où désigne la différence de pression entre les deux faces de la surface, la tension superficielle, caractéristique du liquide dont est constituée cette surface, et la courbure moyenne. Dans le cas d'un film de savon libre, la pression de l'air est la même de chaque côté, donc , par conséquent la courbure moyenne est nulle : on retrouve la définition mathématique de la surface minimale.
Cette représentation a toutefois d'intéressantes limites. En effet, ne peuvent être représentées de cette manière que des équilibres stables de l'énergie potentielle. Imaginons un contour en forme de « chips ». Trois surfaces minimales peuvent s'appuyer sur ce contour, mais seules deux correspondent à des films de savons : la troisième est un équilibre instable, un film de savon « fantôme », c'est le cas correspondant par exemple à une surface d'Enneper.
Coût des matériaux[modifier | modifier le code]

En architecture, l'utilisation de surfaces minimales permet à la fois de minimiser la quantité de matériaux utilisés et de mieux gérer les contraintes physiques en mimant un film de savon sur une armature. Un exemple frappant en est le stade olympique de Munich, qui date de 1972.
Notes et références[modifier | modifier le code]
- Marcel Berger, p. 58.
- William H. Meeks, A survey of the geometric results in the classical theory of minimal surfaces, Bol. Soc. Brasil. Mat. 12, (1981), no.1, p. 29-86.
- (en) « The Costa-Hoffman-Meeks Surface Families » (version du sur Internet Archive).
- (en) Klaus Ecker, « A local monotonicity formula for mean curvature flow », Ann. of Math. 154 (2001), no 2, p. 503-525.
- Une variété de dimension infinie, quelle que soit la définition choisie, n'est pas localement compacte : de fait, elle ne peut pas l'être globalement.
Bibliographie[modifier | modifier le code]
- (en) Marcel Berger, A Panoramic View of Riemannian Geometry, [détail de l’édition]
- (en) Sylvestre Gallot, Dominique Hulin et Jacques Lafontaine, Riemannian Geometry [détail de l’édition]
- Pierre-Gilles de Gennes, Françoise Brochard-Wyart et David Quéré, Gouttes, bulles, perles et ondes, Belin, coll. « Échelles », [détail de l’édition] (ISBN 2701140552)


















