Histoire de la relativité restreinte

1. Isaac Newton
2. James Clerk Maxwell
3. Hendrik Lorentz
4. Henri Poincaré
5. Albert Einstein
6. Hermann Minkowski
L’histoire de la relativité restreinte décrit le développement de propositions et constatations empiriques et conceptuelles, au sein de la physique théorique, qui ont permis d’aboutir à une nouvelle compréhension de l’espace et du temps. Cette théorie, nommée « relativité restreinte », se distingue des travaux ultérieurs d'Albert Einstein, appelés « relativité générale ».
Dans ses Principia mathematica, publiés pour la première fois en 1687 et qui influencent la physique pendant 200 ans, Isaac Newton postule les notions d'espace et de temps absolus et pose la théorie corpusculaire de la lumière. Par la suite, des expériences démontrent que le modèle newtonien ne peut expliquer des phénomènes propres à la nature ondulatoire de la lumière.
En 1864, James Clerk Maxwell publie ses équations qui permettent « d'unifier en une même théorie l'électricité, le magnétisme et l'optique »[1], c'est l'électrodynamique classique. En 1895, Hendrik Lorentz propose ses transformations pour expliquer la contraction des champs électrostatiques. L'« électrodynamique de Maxwell-Lorentz » avance notamment que la masse des électrons augmente lorsqu'ils sont en mouvement. De plus, ses travaux théoriques permettent d'expliquer les résultats de l'expérience de Michelson-Morley, qui n'a pu démontrer l'existence de l'éther. En 1898, par commodité, Henri Poincaré propose que la vitesse de la lumière soit constante dans toutes les directions. Il publiera d'autres articles qui faciliteront la venue de la relativité restreinte. Son influence est tellement grande que des historiens ont avancé qu'il est le créateur de cette théorie, même s'il n'a pas abandonné la notion d'éther.
En 1905, Albert Einstein publie un article d'une trentaine de pages, Zur Elektrodynamik bewegter Körper (De l'électrodynamique des corps en mouvement), qui réconcilie plusieurs contradictions entre les théories de l'époque et les résultats expérimentaux. Pour y parvenir, il énonce deux postulats : le principe de relativité et la constance de la vitesse de la lumière dans tous les systèmes de référence en mouvement uniforme. Des expériences seront réalisées pour tenter d'invalider ou de confirmer les prédictions de la relativité restreinte. Sur le plan théorique, la théorie d'Einstein sera critiquée à plusieurs reprises. Mathématiquement formalisée, surtout grâce aux travaux de Hermann Minkowski, elle s'imposera définitivement pendant le XXe siècle.
Mise en perspective
[modifier | modifier le code]Isaac Newton, dans ses Principia mathematica publiés en 1687 et « qui [ont] défini la physique pendant plus de deux siècles »[2], part d'un espace et d'un temps mathématiquement absolus[3],[4],[5]. Le fait que ces deux entités soient considérées comme absolues n'implique pas que le repère choisi pour y localiser les événements soit unique : ainsi, l'origine du temps peut être choisie de façon arbitraire. Celle de l'espace est définie de façon arbitraire à l'origine du temps, mais de plus, elle peut se déplacer par un mouvement uniforme avec le temps. Et ainsi, sa théorie prévoit aussi le principe de relativité au sens de Galilée, selon lequel tous les observateurs qui se déplacent uniformément l'un par rapport à l'autre ne peuvent pas définir leurs mouvements de façon absolue. Leurs façons de voir sont donc toutes aussi justifiées, et soumises aux transformations de Galilée qui font passer d'un point de vue à l'autre. Il n'existe aucun système de référence privilégié pour tel ou tel observateur. À la fin du XIXe siècle, divers physiciens soulignent que cela peut conduire à envisager une multiplicité d'« espaces absolus » — par exemple Ludwig Lange introduit en 1885 le concept opératoire de référentiel inertiel. Ernst Mach ne trouve pas que le caractère absolu de l’espace et du temps soient suffisamment fondés d'un point de vue phénoménologico-empirique[6].
Pour l’électrodynamique, l'équivalent de l’« espace absolu » de la mécanique est l'« éther ». Ce concept repose sur l'hypothèse, jamais remise en question jusqu'au début du XXe siècle, que des ondes nécessitent pour leur propagation un milieu : comme le son a besoin de l'air, la lumière a besoin de l’éther, que l’on se représente comme une espèce de matière. James Clerk Maxwell formule cette condition de telle sorte que tous les phénomènes optiques et électriques se développent dans un seul milieu. Sous ces conditions, la vitesse de la lumière donnée par les équations de Maxwell est celle relative à l’éther. À la suite de l'hypothèse largement admise à l'époque que l'éther est au repos, et qu'il n’est pas entraîné par la Terre, il serait possible de déterminer le mouvement de la Terre par rapport à l'éther. L'éther définirait ainsi un référentiel remarquable. Cependant tous les essais pour déterminer la vitesse relative de la Terre par rapport à l’éther échouent[7].
Cet état de fait conduit Hendrik Lorentz à partir de 1892 à développer une électrodynamique compatible avec un éther absolu au repos. Dans cette théorie, il devient impossible de détecter la vitesse de l’éther, parce que les corps en mouvement dans l’éther se raccourcissent (contraction des longueurs), tandis que les processus qui y prennent place se ralentissent (dilatation du temps). La cause de ces effets est que les transformations de Galilée sont remplacées par les transformations de Lorentz. Cependant, dans son article décrivant ces résultats en 1904, Lorentz ne peut pas entièrement satisfaire au principe de relativité[8]. Henri Poincaré remarque alors que le caractère fondamental de cette « nouvelle physique » est qu'aucun observateur ne peut dépasser la vitesse de la lumière. En 1905, il réussit à généraliser de façon physiquement complète, et à formaliser de façon mathématiquement élégante l'électrodynamique de Lorentz, en posant le principe de relativité comme une loi universelle de la nature, englobant l'électrodynamique et la gravitation, mais conservant encore l’existence d'un éther et distinguant entre longueurs et temps « vrais » et « apparents », c'est-à-dire dans le référentiel de l'éther et dans celui du corps mobile[9].
En 1905, Albert Einstein arrive enfin, avec la théorie de la relativité restreinte, à une interprétation complètement nouvelle de l'électrodynamique de Lorentz, en bouleversant les concepts d'espace et de temps, et en éliminant l’éther[10],[11]. Einstein déduit ces résultats uniquement à partir des deux postulats qu'il pose : principe de relativité et principe de constance de la vitesse de la lumière dans le vide. La disparition du concept d'éther ne justifie plus la distinction entre coordonnées vraies et apparentes, comme dans les théories de Lorentz et Poincaré. Les recherches sur la relativité restreinte seront poursuivies après Einstein, notamment par Hermann Minkowski qui pose en 1907[12] le cadre formel pour le concept aujourd'hui courant d'espace-temps à quatre dimensions.
Éther et électrodynamique des corps en mouvement
[modifier | modifier le code]Modèles d'éther et équations de Maxwell
[modifier | modifier le code]Au XIXe siècle, la communauté scientifique en est arrivée à la conviction, notamment par les travaux de Thomas Young (1803) et d'Augustin Fresnel[13], que la lumière se propage comme une onde transversale dans un milieu (l'éther luminifère), qui est considéré par beaucoup comme un corps solide élastique. Cependant, les physiciens distinguent les phénomènes optiques et électrodynamiques, c'est-à-dire qu'il faut pour chacune de ces catégories supposer un éther particulier. Et les tentatives pour unifier ces deux variantes d'éther et présenter une description complète sur le plan mécanique de cet éther échouent[14].

Après les travaux préliminaires de physiciens comme Michael Faraday, Lord Kelvin et autres, James Clerk Maxwell en 1864[15] arrive à écrire des équations fondatrices pour l'électricité et le magnétisme, les équations de Maxwell. Il esquisse ainsi un modèle où les phénomènes de l’optique et de l'électrodynamique se rapportent à un seul éther électromagnétique, et où la lumière se définit comme une onde électromagnétique, qui se propage avec une vitesse constante (la « vitesse de la lumière » dans le vide) par rapport à l'éther[16]. En 1873, il déduit une autre conséquence importante de la théorie[17] : l'existence de « contraintes » électrostatiques et magnétiques, qui peuvent exercer une pression sur les corps. Une conséquence immédiate en est la pression de radiation exercée par la lumière. Adolfo Bartoli déduit l'existence de cette même pression en 1876[18] par des considérations thermodynamiques[19].
Après que Heinrich Hertz (1887) démontre expérimentalement l'existence d'ondes électromagnétiques, la théorie de Maxwell devient enfin largement acceptée. Oliver Heaviside en 1889[20] et Hertz en 1890[21],[22] introduisent des versions modernisées des équations de Maxwell, qui forment une base importante des développements ultérieurs de l'électrodynamique (équations de Maxwell-Hertz et de Heaviside-Hertz). C'est la forme donnée par Heaviside qui s'impose généralement[23],[24]. Hertz restera un des derniers partisans de l’« image du monde mécaniste », selon laquelle tous les processus électromagnétiques doivent être attribués à des effets de collisions et de contacts dans l'éther[25].
L'éther introuvable
[modifier | modifier le code]
En ce qui concerne l'état de mouvement de l'éther par rapport à la matière, on peut prendre en compte deux possibilités de principe :
- la position de Fresnel en 1818[26], et plus tard de Lorentz en 1892[27], d'un éther au repos, ou tout au moins seulement partiellement entraîné par la matière[28] ; ou
- celle de George Gabriel Stokes en 1845[29], adoptée plus tard par Hertz en 1890[22], d'un entraînement complet de l’éther par la matière[30].
La théorie de Fresnel est préférée, parce qu'on peut dans ce cadre expliquer l’aberration de la lumière et de nombreux autres phénomènes optiques, et parce que le coefficient d'entraînement a pu être mesuré par Hippolyte Fizeau[31] avec une grande précision par l'expérience de Fizeau. Par contre, la théorie de Stokes ne parvient pas à s'imposer, car elle contredit aussi bien l'aberration que le résultat de l’expérience de Fizeau. Ces hypothèses introduites ad hoc pour obtenir ces résultats sont peu convaincantes, ou carrément contradictoires (par exemple, Stokes propose que les ondes lumineuses subissent une réfraction à proximité de la Terre car elle entraîne un hypothétique éther, ou encore que l'éther est un milieu très rigide pour les ondes à hautes fréquences et un milieu très fluide pour les ondes à basses fréquence)[32].


Albert Abraham Michelson en 1881[33] essaie de mesurer directement le mouvement relatif de la Terre et de l'éther (le « vent d'éther »), qui devrait avoir lieu selon la théorie de Fresnel. Cependant, avec son système d'interférométrie, il n'arrive pas à trouver le résultat qu'il attend, et interprète ce résultat négatif comme une preuve en faveur de la théorie de Stokes (entraînement complet de l’éther par la Terre), et donc à l'encontre de celle de Fresnel[34]. En 1886, Lorentz[35] démontre cependant que Michelson a fait une faute de calcul, et que l'expérience est trop imprécise pour donner un résultat probant dans les limites de l'erreur, ce qui est reconnu par Michelson[30]. Comme la théorie de Fresnel semble alors subsister, Michelson et Edward Morley[36] font une nouvelle expérience pour vérifier le coefficient d'entraînement mesuré par Fizeau. Cette confirmation réussit, et Michelson, à l'encontre de son assertion de 1881, est de l'opinion que l'éther au repos de Fresnel est ainsi confirmé[37]. Ceci exige de répéter l'expérience de Michelson de 1881, ce qui conduit, à la grande surprise de Michelson et Morley, à ce que cette expérience aujourd'hui célèbre en physique sous le nom d'expérience de Michelson-Morley, ne fournisse pas, une fois encore, le résultat positif attendu. À nouveau, l'expérience semble confirmer l'éther de Stokes, qui a pourtant déjà été contredit, et elle se situe en grossière contradiction avec l'expérience de 1896, qui favorise l'éther de Fresnel[38].
La théorie de Voigt de 1887
[modifier | modifier le code]Dans les années 1880, Woldemar Voigt développe[39], sur la base d'un modèle d'éther élastique (différent de celui de Maxwell), et dans la ligne des recherches sur l'effet Doppler, une transformation des coordonnées entre un système au repos dans l'éther et un système en mouvement. Les équations de la transformation de Voigt laissent l'équation d'onde inchangée. Elles sont, à un facteur d'échelle près, identiques aux transformations de Lorentz, et peuvent expliquer l’expérience de Michelson-Morley. Elles comprennent l'expression connue ultérieurement sous le nom de « facteur de Lorentz »
pour les coordonnées et et une nouvelle variable temporelle nommée ultérieurement « temps local »
étant le temps mesuré par l'observateur, étant la vitesse de l'objet mesurée par l'observateur et étant la vitesse de la lumière dans le vide. Cependant, ces équations ne sont pas symétriques, et se heurtent par suite au principe de relativité. Voigt a été le premier à en déduire les équations de transformation du type de Lorentz[40], mais ce travail reste complètement ignoré de ses contemporains[41],[42]. Comme le souligne H. A. Lorentz dans une note de bas de page 198 de son livre Theory of Electrons[43], Voigt a donc prévu les transformations de Lorentz[44]. Le travail de pionnier de Voigt en 1887 doit avoir été connu du créateur de la théorie moderne de la relativité, parce que ce travail a été cité en 1903 dans les Annalen der Physik[45] et Voigt a aussi correspondu avec Lorentz en 1887 et 1888 sur l'expérience de Michelson-Morley. Il est également certain que Joseph Larmor[46] connaissait la transformation de Voigt.
Il se présente cependant une autre possibilité d'explication : Heaviside en 1889[20] et George Frederick Charles Searle en 1897[47] établissent que les champs électrostatiques sont contractés dans la direction du mouvement (ellipsoïde d'Heaviside)[48]. À la suite de ces travaux d'Heaviside, George FitzGerald en 1889[49] introduit l’hypothèse ad hoc que les corps matériels se contractent également dans la direction du mouvement, ce qui conduit à la contraction des longueurs, et pourrait expliquer l'expérience de Michelson-Morley. Au contraire de ce qui se passe dans les équations de Voigt, la coordonnée x est ici aussi transformée. FitzGerald s'appuie sur le fait que les forces intermoléculaires peuvent être d'origine électrique. Cependant son idée n'est pas diffusée au début, et n'est connue que par une publication d'Oliver Lodge en 1892[50]. Indépendamment de FitzGerald, Lorentz en 1892[51] propose la même hypothèse (« hypothèse de contraction de FitzGerald-Lorentz »). Parmi les arguments de plausibilité, il mentionne aussi l'analogie avec la contraction des champs électrostatiques, tout en concédant que ce n'est nullement un argument contraignant[52],[53].
La théorie de Lorentz de 1895
[modifier | modifier le code]
Lorentz en 1892[27] et surtout en 1895[54] pose les fondements de l'électrodynamique de Maxwell-Lorentz, ou théorie de l’éther et des « particules qui prennent part aux mouvements électromagnétiques », en supposant outre l'éther, et comme d'autres avant lui, l'existence de ces particules (qui n'existent pas dans l'éther). Il présuppose que l'éther est complètement au repos, et n'est pas entraîné par les particules. Il en découle la conséquence importante que la vitesse de la lumière est totalement indépendante de la vitesse de sa source, et par suite, dans un système de coordonnées où l'éther est au repos, constante dans tous les cas de figure. Au lieu de faire des assertions sur la nature mécanique de l’éther et des processus électromagnétiques, il essaie inversement de rapporter de nombreux processus mécaniques à une cause électromagnétique. Dans le cadre de sa théorie, Lorentz calcule (comme Heaviside) la contraction des champs électrostatiques, ce qui le conduit à définir indépendamment du travail de Voigt le temps local. Ainsi, il dispose d'une forme préliminaire de ce qui est connue plus tard sous le nom de transformations de Lorentz, qui sert à expliquer le résultat négatif de toutes les expériences de dérive dans l’éther pour des grandeurs à l'ordre v / c. Pour ceci, il utilise en 1895 le concept de « théorème des états correspondants », c'est-à-dire la covariance des équations de Maxwell par transformations de Lorentz pour des vitesses suffisamment faibles (par rapport à celle de la lumière). Il s'ensuit que la forme des équations électromagnétiques d'un système « réel » (au repos dans l'éther) correspond à celle d'un système « apparent » (en mouvement dans l'éther). Cependant, Lorentz reconnaît que sa théorie va à l'encontre du principe de l’action et de la réaction, car l'éther peut agir sur la matière, tandis que la matière ne peut pas réagir sur l’éther[55].
Joseph Larmor en 1897-1900[56],[57] esquisse un modèle très voisin de celui de Lorentz, cependant il fait un pas de plus, et met la transformation de Lorentz sous une forme algébriquement équivalente, qui est encore utilisée de nos jours. Il voit qu'on peut en déduire non seulement une contraction des longueurs, mais aussi une espèce de dilatation du temps, qui fait que la rotation d'électrons en mouvement dans l’éther est plus lente que celle d'électrons au repos[58]. Il peut montrer que cette transformation est valable jusqu'au second ordre en v / c, mais il ne peut rien dire des ordres supérieurs. En 1899, Lorentz[59] étend aussi sa transformation aux grandeurs du second ordre (avec toutefois un facteur inconnu), et note, comme le fait Larmor, une espèce de dilatation du temps. On ne sait pas dans quelle mesure Larmor et Lorentz se sont influencés l'un l'autre ; c'est-à-dire qu'on ne sait pas si Larmor en 1897[56] a repris le temps local de Lorentz, ni si en revanche Lorentz en 1899[59] a repris la transformation complète de Larmor. Chacun cite les articles de l’autre, ils restent en contact par lettre, mais ils n'y parlent pas de la transformation de Lorentz[42].
Il y a cependant des modèles alternatifs à ceux de Lorentz et de Larmor. Emil Cohn esquisse en 1900 une électrodynamique, où, parmi les premiers, il rejette l'idée d'éther — du moins sous sa forme d'alors — et où il utilise, comme Ernst Mach, les étoiles fixes pour définir le système de référence. Il peut ainsi expliquer l'expérience de Michelson-Morley, puisque la Terre est au repos par rapport aux étoiles fixes, cependant dans sa théorie, la vitesse de la lumière dans des milieux matériels peut être dépassée simultanément dans différentes directions. La théorie est rejetée plus tard (par Cohn lui-même) à cause de ses imperfections. Ultérieurement, il discute aussi de la théorie de Lorentz et utilise le concept de transformation de Lorentz[60].
Masse électromagnétique
[modifier | modifier le code]
Joseph John Thomson en 1881[61] reconnaît, pendant son développement de l'électrodynamique de Maxwell, que les champs électrostatiques se comportent comme s'ils apportaient aux corps électriquement chargés une « masse électromagnétique » outre leur masse mécanique. Ceci est alors interprété comme une conséquence de l'induction électromagnétique des courants de convection dans l'éther. Il reconnaît de plus que cette masse augmente pour des corps en mouvement, d'un même facteur pour toutes les vitesses non nulles[62],[63],[25]. FitzGerald, Heaviside et Searle commencent par corriger quelques fautes, et continuent le travail de Thomson. Ils trouvent comme expression de la masse électromagnétique (en notation moderne)
où est l'énergie électromagnétique et la vitesse de la lumière dans le vide.
En 1888, Heaviside[64] reconnaît de plus que l'augmentation de masse électromagnétique des corps en mouvement n'est pas constante, mais augmente constamment quand la vitesse augmente. En 1897, Searle[47] en déduit que cela rend impossible de dépasser la vitesse de la lumière, puisqu'il faudrait pour cela dépenser une énergie infinie. Cette circonstance est intégrée par Lorentz en 1899[59] dans sa théorie. Il remarque qu'en raison de la transformation de Lorentz, la masse ne varie pas seulement avec la vitesse, mais aussi avec la direction, et il introduit les termes, nommés plus tard par Max Abraham, « masse longitudinale » et « masse transverse » — où seule la « masse transverse » deviendra plus tard la masse relativiste[65].
Wilhelm Wien en 1900[66] (précédé par Larmor et Emil Wiechert) défend, sur la base de la théorie de Lorentz, le point de vue que — à l'inverse de l'« image mécanique du monde » de Hertz — toutes les forces de la nature sont explicables par l'électromagnétisme (« image électromagnétique du monde »)[67]. À la suite de quoi, il suppose que toute la masse est d'origine électromagnétique, ce qu'il écrit
en utilisant l'expression de Thomson-Heaviside-Searle pour la masse électromagnétique. Il remarque aussi que la gravitation doit être proportionnelle à l'énergie électromagnétique, au cas où elle doit prendre en compte aussi l'énergie électromagnétique. Dans la même revue, Poincaré[68] déduit des contraintes maxwelliennes évoquées ci-dessus et, de la théorie de Lorentz, l'impulsion électromagnétique et conclut, en liaison avec le principe d'action-réaction, que l'énergie électromagnétique correspond à une masse « fictive » de
ou
— mais tout en considérant ces êtres comme des fictions mathématiques. Il se heurte néanmoins à un paradoxe du rayonnement, qui n'a été résolu de façon satisfaisante qu'ultérieurement par Einstein[69].
Walter Kaufmann en 1902[70] et en 1905[71] est le premier à confirmer expérimentalement que la masse électromagnétique est fonction de la vitesse. Il fabrique des rayons cathodiques d'électrons de charge électrique, de vitesse et de masse mesurables. Comme on sait déjà que la charge d'un électron est indépendante de sa vitesse, et que le résultat obtenu par Kaufmann expérimentalement donne une décroissance du rapport charge/masse pour des vitesses se rapprochant de celle de la lumière, ceci ne peut être interprété que comme une croissance de la masse des électrons étudiés. Kaufmann croit par là avoir démontré que ses mesures indiquent que toute la masse de la matière est d'origine électromagnétique[72].

Max Abraham en 1902-1903[73],[74], qui est comme Wien un partisan convaincu de l'image électromagnétique du monde, prolonge la théorie commencée par Lorentz. Il est ainsi le premier à proposer une conception de l'électron fondée sur une théorie des champs. Contrairement à Lorentz, il définit l'électron comme un corps sphérique rigide, et refuse sa contraction, ce pourquoi ses termes de masse diffèrent de ceux de Lorentz (raison pour laquelle il est le premier à formuler les concepts de masse longitudinale et de masse transverse). De plus, à la suite de Poincaré, il introduit le concept d'impulsion électromagnétique, proportionnelle à E / c2. Contrairement à Poincaré et à Lorentz, il les considère comme des entités physiques réelles. La théorie d'Abraham devient dans les années suivantes le plus important des modèles concurrents à la théorie de Lorentz. Mais les expériences de Kaufmann n'ont pas la précision nécessaire pour départager les théories[75].
Enfin, Friedrich Hasenöhrl relie l'énergie à l'inertie, dans un article de 1904[76], qui est, dans ses propres termes, très voisin de celui d'Abraham. Hasenöhrl suppose qu'une partie de la masse d'un corps (la « masse apparente ») peut être recueillie sous forme de rayonnement dans une cavité. L'inertie de ce rayonnement est proportionnelle à son énergie par la formule
Il remarque à ce propos le rapport étroit entre le travail mécanique, la température et la masse apparente, puisque tout échauffement provoque du rayonnement et donc de l’inertie supplémentaire. Cependant Hasenöhrl limite cette relation entre énergie et masse apparente à des corps rayonnants ; c'est-à-dire pour un corps dont la température excède 0 K. Il publie néanmoins en 1905[77] le résumé d'une lettre que lui a envoyée Abraham, qui y critique le résultat, et indique comme valeur pour la masse apparente corrigée
c'est-à-dire la même valeur que pour la masse électromagnétique déjà connue. En revoyant ses propres calculs, Hasenöhrl confirme le résultat d'Abraham[78].
Espace et temps absolus
[modifier | modifier le code]La définition par Newton de l’espace et du temps absolus commencent à être mises en question par certains auteurs[79],[80]. Par exemple, Carl Neumann en 1870[81], remplace n'importe quelles grandeurs absolues par un « corps alpha », un corps rigide et immobile, par rapport auquel les mouvements inertiels peuvent être définis. Ernst Mach en 1883[82] argumente que des concepts tels que l'espace et le temps absolus sont vides de sens, et que seule la notion de mouvement relatif en a un. Il est même d'avis que des mouvements accélérés comme la rotation peuvent être rendus relatifs à des « masses lointaines », sans devoir introduire un espace absolu. L'argumentation de Neumann est poursuivie par Heinrich Streintz[83]. Quand des mesures par gyroscopes ne montrent aucune rotation, Streintz affirme que l'on peut parler d'un mouvement inertiel par rapport à un « corps fondamental » ou un « système de coordonnées fondamental ». Finalement, Ludwig Lange en 1885[84] est le premier à abstraire de ces considérations la notion de système inertiel, pour éliminer les grandeurs absolues de la cinématique. Il définit un tel système comme[80] : « un système tel que par rapport à lui, si l'on projette trois points, non alignés, simultanément du même point d'espace, et qu'on les laisse alors immédiatement libres, et si leurs trajectoires sont décrites uniformément et convergent, alors ces trajectoires sont toutes trois rectilignes. » De plus, Henri Poincaré en 1902[85] publie le livre philosophique et de vulgarisation scientifique La Science et l’Hypothèse, qui comporte en particulier (1) des chapitres philosophiques sur la relativité de l’espace, du temps et de la simultanéité, (2) les expressions « principe de mouvement relatif » et « principe de relativité », (3) l'idée que l'on ne pourra jamais découvrir l'éther, c'est-à-dire la validité du principe de relativité, (4) la possibilité de la non-existence de l’éther — mais aussi des arguments en faveur de l'éther et (5) des exposés détaillés des géométries non euclidiennes de Riemann et de Lobatchevsky[n 1].

Des spéculations sur le temps en tant que quatrième dimension se font jour[86],[87]. Par exemple, c'est ce qu'avait fait dès 1754 Jean d'Alembert dans l’Encyclopédie, ainsi que divers auteurs du XIXe siècle comme Menyhért Palágyi, qui développe en 1901 un modèle philosophique où l'espace et le temps ne forment que des désignations verbales pour une « forme d'espace-temps » en réalité unitaire[88]. Il y utilise en fait comme quatrième dimension la variable i t où i est l'unité imaginaire. Cependant, il n'y a dans la philosophie de Palágyi aucune relation avec le temps local de Lorentz, car chez lui la dimension de temps n'est pas reliée à la vitesse de la lumière. Il rejette aussi tout rapport avec les constructions déjà faites d'espaces à n dimensions et de géométrie non euclidienne. Significativement, ce n'est que plus tard (1915) que Palágyi se rattachera aussi aux constructions d'espace-temps de Minkowski et d'Einstein — et c'est pour cela que ses critiques considèrent que sa théorie n'a pas grand-chose à voir avec la théorie de la relativité[89].
Principe du mouvement relatif et synchronisation des horloges
[modifier | modifier le code]
Dans la deuxième moitié du XIXe siècle, on s'occupe de façon intensive à construire un système mondial d'horloges synchronisées par des signaux électriques, ce qui nécessite de prendre en compte la vitesse finie de la lumière. En 1898, Henri Poincaré[90] en tire des conséquences lourdes pour la philosophie et la physique. Il établit que la synchronisation par signaux lumineux a en soi une signification pour la définition de la simultanéité en divers endroits, et que par suite la définition de la simultanéité est une pure convention de commodité. De plus, il argumente que l'hypothèse d'une vitesse constante de la lumière dans toutes les directions (par exemple pour l'astronomie) est avantageuse comme postulat, pour donner à des lois, telle que la loi de la gravitation de Newton, une forme aussi simple que possible[91]. Dans des travaux ultérieurs, en 1895 et en 1900[92],[93], il explique qu'il ne croit pas à un mouvement absolu, ou encore à la possibilité de découvrir un mouvement par rapport à l'éther, et nomme cette opinion « principe du mouvement relatif »[94]. La même année, Poincaré[68] reconnaît que l'on peut définir le temps local de Lorentz par le fait que deux observateurs synchronisent leurs horloges au moyen de signaux lumineux (synchronisation de Poincaré-Einstein). Quand ils supposent, en vertu du principe de relativité, qu'ils sont chacun au repos, ils en déduisent, chacun dans son système de coordonnées, que la vitesse de la lumière est la même dans toutes les directions. Si par contre, ils étaient en mouvement par rapport à l’éther, ce dernier résultat ne serait pas vrai, et ils ne pourraient pas synchroniser leurs horloges (relativité de la synchronisation). Ainsi, Poincaré définit le temps local comme une grandeur physiquement interprétable, qui peut être indiquée par des horloges — en contradiction patente avec l'interprétation purement mathématique de Lorentz[95].
En 1903, Alfred Bucherer[96] explique comme Poincaré que seuls les mouvements relatifs des corps entre eux peuvent être établis, mais pas ceux relatifs à l'éther. Contrairement à Poincaré, il en conclut que le concept d'éther luminifère doit être complètement abandonné. La théorie construite ainsi par Bucherer n'est cependant pas utilisable, tant du point de vue expérimental que par ses fondements théoriques — car Bucherer, malgré son rejet du concept de l’éther, n'en tire aucune conséquence en rapport avec la relativité de l'espace et du temps[97].
La théorie de Lorentz de 1904
[modifier | modifier le code]Sous l'influence de l'exigence de Poincaré de l'impossibilité de découvrir un mouvement absolu, Lorentz en 1904[98] se rapproche beaucoup de l'achèvement de son théorème des états correspondants. Il a développé comme Abraham une théorie des champs pour l'électron, qui, contrairement à celle d'Abraham, essaie de prendre en compte la contraction des électrons, et ainsi le principe de relativité. Il peut donc, en utilisant l'impulsion électromagnétique, expliquer le résultat négatif de l’expérience de Trouton-Noble (1903), qui cherche à confirmer qu'un couple est observé sur un condensateur plan à cause du vent d'éther. De même les résultats négatifs des expériences de Rayleigh et Brace (1902 et 1904) sur la biréfringence peuvent être expliqués. Un important pas en avant est d'étendre la validité de la transformation de Lorentz aux forces non électriques (dans la mesure où elles existent). Lorentz n'arrive cependant pas à montrer la covariance de Lorentz complète des relations électromagnétiques[99].

À peu près au moment où Lorentz développe sa théorie, Wien[100] établit, comme avant lui Searle en 1897[47], qu'en raison de la variation de la masse en fonction de la vitesse, il serait nécessaire de disposer d'une énergie infinie pour atteindre la vitesse de la lumière, ce qui serait donc impossible. Et après avoir vu la formulation complète de la théorie de Lorentz, Wien déduit[101] la même chose en raison de la contraction des longueurs, puisque la longueur d'un corps en mouvement au-dessus de la vitesse de la lumière serait imaginaire pure[102].
En 1904, Abraham[103] pointe cependant un défaut fondamental dans la théorie de Lorentz. Elle est d'une part construite pour que soit satisfait le principe de relativité, mais d'autre part elle suppose démontrée une origine électromagnétique à toutes les forces. Abraham montre que ces deux hypothèses ne sont pas compatibles, puisque dans la théorie de Lorentz, les électrons contractés ont besoin d'une énergie de liaison non électrique, qui garantit la stabilité de leur état matériel. Dans la théorie d'Abraham de l’électron rigide, cette énergie n'est pas nécessaire[104]. Il se pose donc la question de savoir lequel des deux est correct : l'image électromagnétique du monde (compatible avec la théorie d'Abraham) ou le principe de relativité (compatible avec la théorie de Lorentz)[65],[105].
En , dans un exposé donné à St. Louis, Poincaré définit, en considérant déjà la nouvelle théorie de Lorentz et à l'aide du lien entre le principe de relativité galiléen et le théorème de Lorentz des états correspondants, le « principe de relativité » comme une exigence selon laquelle les lois de la nature doivent être les mêmes pour tous les observateurs[106]. Ces lois s'appliquent indépendamment du fait qu'ils soient ou non en mouvement, donc leur état de mouvement absolu est inconnaissable. Il précise sa méthode de synchronisation des horloges par la lumière, et ainsi son interprétation physique du temps local, et explique qu'on introduira peut-être une « nouvelle méthode » ou une « nouvelle physique » fondée sur l'impossibilité de dépasser la vitesse de la lumière, même pour les observateurs en mouvement par rapport à l'éther. Il remarque cependant, de façon critique, que le principe de relativité, le principe d'action-réaction de Newton, les théorèmes de conservation de la masse et de l'énergie, ne sont pas à l'abri d'une nouvelle conception[107].
En , Cohn[108] montre des possibilités d'interprétation physique de la théorie de Lorentz — qu'il compare à la sienne. Il s'y réfère au rapport étroit entre mesures avec des règles et des horloges. Quand ceux-ci sont au repos dans l’éther de Lorentz, ils montrent les longueurs et temps « vrais », mais quand ils sont en mouvement, ils donnent des valeurs respectivement contractées et dilatées. Cohn fait, comme Poincaré, l'observation importante que l’heure locale survient quand la lumière se propage sur la Terre comme une onde sphérique, c'est-à-dire quand la propagation de la lumière sur la Terre est considérée comme isotrope. Contrairement à Lorentz et à Poincaré, Cohn établit que la différence entre coordonnées vraies et apparentes dans la théorie de Lorentz paraît très artificielle, puisqu'aucune expérience ne peut montrer le vrai état de mouvement, et toutes les coordonnées sont également justifiées. Cependant, Cohn pense que tout ceci n'est valable que dans le domaine de l’optique, mais que par contre les horloges mécaniques pourraient indiquer le temps « vrai »[60].
Dynamique de l'électron de Poincaré
[modifier | modifier le code]Le , Poincaré dépose enfin le résumé d'un travail qui comble formellement les dernières lacunes du travail de Lorentz. Cet écrit comprend beaucoup de résultats, parmi lesquels des parties importantes[109] sont contenues dans deux lettres écrites à Lorentz par Poincaré vers [110],[111]. Il parle du postulat de la totale impossibilité de découvrir le mouvement absolu, qui semble être une loi de la nature. Il reconnaît le caractère de groupe de ce qu'il est le premier à nommer les transformations de Lorentz, il leur donne leur forme symétrique moderne, et en utilisant la formule relativiste de composition des vitesses, il corrige les termes de Lorentz pour la densité de charge et la vitesse, et obtient ainsi une covariance de Lorentz complète. À la suite de Lorentz, il explique que la transformation de Lorentz (et par suite l'invariance de Lorentz) doivent être appliquées à toutes les forces de la nature. Mais contrairement à Lorentz, il considère également la gravitation, affirme la possibilité d'un modèle de la gravitation invariant de Lorentz, en évoquant l’existence d'ondes gravitationnelles. Pour désarmer les critiques d'Abraham, Poincaré introduit une contrainte non électrique (les « contraintes de Poincaré »), afin de garantir la stabilité de l’électron et éventuellement servir de fondement dynamique à la contraction des longueurs. Ainsi, Poincaré abandonne l'image électrodynamique du monde en faveur du principe de relativité[65],[112].
Enfin, comme annoncé dans sa note aux comptes rendus du , Poincaré fournit son travail (déposé le , imprimé le , publié en ), indépendamment d'Einstein[n 2], article connu sous le nom de « travail de Palerme » qui présente une version substantiellement étendue de son premier travail publié en 1905. Il parle du « postulat de relativité » ; il montre que les transformations sont une conséquence du principe de moindre action, démontre plus en détail que précédemment que les transformations forment un groupe, pour lequel il invente le nom de « groupe de Lorentz ». Il traite en détail les propriétés des contraintes de Poincaré. En relation avec sa conception de la gravitation (qui se trouva toutefois insuffisante), Poincaré montre que la combinaison
est invariante. Il introduit l'expression
(contrairement à Palágyi, il y introduit en facteur la vitesse de la lumière ) comme quatrième coordonnée d'un espace quadridimensionnel en utilisant une sorte de quadrivecteur. Cependant, en 1907, Poincaré remarque qu'une nouvelle formulation de la physique dans un langage à 4 dimensions est certainement possible, mais trop compliquée, et par suite de peu d'utilité, ce qui le conduit à ne pas poursuivre ses travaux à ce sujet, ce qui sera fait par Minkowski ultérieurement. Mais contrairement à Einstein, Poincaré continue à adhérer au concept d'éther[113],[114].
Théorie de la relativité restreinte
[modifier | modifier le code]
Einstein en 1905
[modifier | modifier le code]Théorie de la relativité restreinte
[modifier | modifier le code]Albert Einstein publie dans son article Zur Elektrodynamik bewegter Körper (Sur l'électrodynamique des corps en mouvement — soumis le , publié le )[116], avec sa théorie maintenant nommée relativité restreinte, une base complètement nouvelle pour résoudre ce problème. Non seulement, il arrive à déduire les parties essentielles de l'électrodynamique de Lorentz, mais la théorie contient une élimination de l’éther, et un changement des bases conceptuelles de l’espace et du temps. Ceci repose seulement sur deux principes : le principe de relativité et la constance de la vitesse de la lumière dans tous les systèmes de référence en mouvement uniforme. Pour comprendre l'avancée d'Einstein, il faut rappeler encore ici la situation de départ, en particulier les hypothèses théoriques et expérimentales (Einstein déclare avoir lu la théorie de Lorentz de 1895, et La Science et l'Hypothèse de Poincaré[85], mais pas leurs travaux de 1904-1905)[n 2] :
b) l'impossibilité de trouver un état de mouvement absolu, conséquence de toutes les expériences sur le vent d'éther, ainsi que le fait que les effets de l'induction électromagnétique ne dépendent que de la vitesse relative.
c) l'expérience de Fizeau.
Pour la vitesse de la lumière et les théories alors en discussion, ces points ont les conséquences suivantes :
- La vitesse mesurée de la lumière n'est pas la composition de la vitesse de la lumière dans le vide et de celle du système utilisé, à cause de b). Ceci est en contradiction avec la théorie de l’éther au repos ou partiellement entraîné.
- La vitesse mesurée de la lumière n'est pas la composition de la vitesse de la lumière dans le vide et de la vitesse de la source, à cause de a) et c). Ceci est en contradiction avec la théorie de l'émission de Newton.
- La vitesse mesurée de la lumière n'est pas la composition de la vitesse de la lumière dans le vide et de la vitesse d'un milieu entraîné au sein, ou à proximité de la matière, en raison de a), c) et d). Ceci est en contradiction avec la théorie de l'entraînement complet de l'éther.
- La vitesse mesurée de la lumière dans des milieux en mouvement n'est pas la composition de la vitesse de la lumière dans le milieu au repos et de la vitesse du milieu, mais suit le coefficient d'entraînement de Fresnel, par c).
Maintenant, il est toujours possible d'introduire des hypothèses ad hoc pour sauver une théorie donnée, cependant en science, une telle coïncidence d'effets destinée à empêcher telle ou telle découverte est considérée comme tout à fait improbable. Si l’on abandonne, comme Einstein, les hypothèses additionnelles et les propriétés inobservables, il découle des observations ci-dessus[n 3] la validité immédiate du principe de relativité et de la constance de la vitesse de la lumière dans tous les systèmes inertiels. Poincaré et Lorentz utilisent ces principes comme Einstein, ils enseignent l'équivalence mathématique complète entre systèmes de référence inertiels, et reconnaissent que des coordonnées différentes d'espace et de temps peuvent être mesurées. Pour eux les effets de la transformation de Lorentz sont dues à des interactions dynamiques avec l'éther, et ils distinguent entre le temps « vrai » du système au repos de l'éther et le temps « apparent » des systèmes en mouvement par rapport à celui-là. Ils évoquent l’éther jusque dans leurs derniers écrits. Concrètement, cela signifie qu'ils sont prêts à modifier la mécanique de Newton, mais pas à la changer complètement. La conséquence en est que l'asymétrie fondamentale de la théorie de Lorentz, c'est-à-dire les concepts exclusifs d'« éther au repos » et du principe de relativité, coexistent encore dans les concepts de la théorie, reliés uniquement par un système d'hypothèses adjuvantes. La solution de cette problématique, soit la nouvelle conception fondamentale de l'espace et du temps dans le cadre d'une théorie scientifique, reste au crédit d'Einstein. L'abandon de l'éther lui paraît plus facile qu'à nombre de ses contemporains, sans doute parce qu'il a reconnu, dans son travail sur la théorie des quanta, la nature corpusculaire de la lumière. Ainsi, le schéma classique des ondes électromagnétiques, qui ont besoin d'être supportées par un éther, n'a plus pour Einstein une aussi grande importance que par exemple pour Lorentz[117],[118].
Avec sa méthode axiomatique, Einstein n'a besoin que de quelques pages pour déduire des résultats sur lesquels d'autres ont buté pendant des années dans un travail compliqué. Einstein explique que l'apparente contradiction entre les deux principes qu'il prend comme postulats de sa théorie peut être levée par l'étude de l’espace, du temps et de la simultanéité. L'introduction d'un éther devient alors superflue, ce qu'il explique dans l'introduction de Zur Elektrodynamik bewegter Körper, article divisé en sections numérotées § 1., § 2., etc.[116]. À partir de la synchronisation des horloges par des signaux lumineux, et la relativité de la simultanéité qui en découle (§§ 1-2), il déduit dans le § 3 la transformation de Lorentz par des considérations purement cinématiques. De cette transformation, il tire comme conséquences secondaires (§§ 4-5) la contraction des longueurs, la dilatation du temps et le théorème d'addition relativiste des vitesses. À la fin de l'article (§§ 6-10), il applique les résultats à l'électrodynamique. Il déduit des transformations l'effet Doppler relativiste et l'aberration relativiste, montre la covariance de Lorentz des équations de Maxwell et calcule les expressions relativistes de la pression de radiation. Enfin, il calcule les masses longitudinale et transverse de l'électron (avec une faute de calcul sur la seconde).[réf. souhaitée]
Équivalence de la masse et de l’énergie
[modifier | modifier le code]Déjà dans le dernier paragraphe de l'article cité, Einstein donne l'énergie cinétique d'un électron sous la forme :
La question reste cependant ouverte de savoir si cette relation n'a de signification que pour l'énergie cinétique, comme en mécanique classique, ou si elle a un équivalent pour l'énergie interne. En , Einstein[119] montre au moyen d'un paradoxe de rayonnement, qui a déjà été formulé par Poincaré en 1900[68], mais non résolu, que des corps au repos gagnent par apport d'une énergie E une masse quel que soit le signe de E, ce qui conduit à une équivalence masse-énergie selon la formule E=mc2[69]. Des formules semblables pour la « masse électromagnétique » ont déjà été établies, comme expliqué ci-dessus, par Thomson, Poincaré, Hasenöhrl, etc., mais aucun de ces auteurs n'a entièrement compris la signification de cette formule. Par contre, Einstein peut montrer le rapport profond entre équivalence et principe de relativité, et en outre, sa preuve est complètement indépendante de la question de la nature, électrodynamique ou non, de la masse.
Premier accueil
[modifier | modifier le code]Premières évaluations
[modifier | modifier le code]Walter Kaufmann[71],[120] est le premier à porter attention au travail d'Einstein. Il compare les théories de Lorentz et d'Einstein, et bien qu'il préfère la méthode d'Einstein, il établit l'équivalence entre les deux théories du point de vue de l’observateur. C'est pourquoi il parle du principe de relativité comme l'« hypothèse fondamentale de Lorentz-Einstein ». Max Planck — qui va jouer un rôle décisif dans la diffusion de la théorie de la relativité, notamment en gagnant ses étudiants Max von Laue et Kurd von Mosengeil à cette théorie — parle dans son premier article sur la relativité restreinte[121] de la théorie de « Lorentz-Einstein », car le principe de relativité a été introduit par Lorentz puis par Einstein « sous une forme plus générale ». Par ailleurs, le nom de Poincaré est peu cité dans les articles au début de l'histoire de la relativité. Planck est aussi le premier, dans un article ultérieur[122], à introduire l'expression raccourcie « théorie relative » pour « théorie de Lorentz-Einstein » en contraste avec la « théorie sphérique » d'Abraham. Dans la discussion qui suit ce travail, c'est Alfred Bucherer qui introduit l'expression « théorie de la relativité » (d'Einstein). Beaucoup (y compris Einstein) n'utilisent encore que l’expression « principe de relativité » pour la nouvelle méthode. Toutes ces dénominations sont tour à tour utilisées par divers physiciens. Dans un article résumant sa théorie[123], Einstein décrit la relativité restreinte comme une « unification de la théorie de Lorentz avec le principe de relativité » tout en faisant l'hypothèse majeure que le temps local de Lorentz est un temps réel et légitime[124].
Expériences de Kaufmann, Bucherer et Neumann
[modifier | modifier le code]
Kaufmann fait alors connaître les résultats de ses nouvelles expériences[71],[120]. D'après lui, elles contredisent sans équivoque le principe de relativité et la « théorie de Lorentz-Einstein », tandis qu'elles sont en bon accord avec la théorie d'Abraham. Pendant quelques années, les expériences de Kaufmann constituent un obstacle majeur à la reconnaissance du principe de relativité. Cependant, la force prédictive des expériences est remise en question par Planck et Adolf Bestelmeyer en 1906[125].
En 1908, Alfred Bucherer fait de nouvelles expériences (voir l'image ci-contre) afin de vérifier celles de Kaufmann[126]. Cette fois, le résultat des expériences est compatible avec la « théorie de Lorentz-Einstein » et le principe de relativité. Cependant, quelques doutes demeurent.
Des expériences ultérieures de Neumann en 1914[127] et d'autres donnent encore des résultats en faveur de la théorie de la relativité, si bien que beaucoup de physiciens en arrivent à la conviction que l'affaire est entendue. Cependant, des recherches ultérieures montrent que les expériences de Kaufmann, de Bucherer et de Neumann en elles seules ne sont pas suffisamment précises pour arbitrer entre les théories concurrentes. Ce n'est qu'en 1940 qu'on pourra définitivement confirmer par ce type d'expérience la formule de Lorentz-Einstein[125]. Mais ce genre de problème ne subsiste que pour cette catégorie d'expériences. Les recherches sur la structure fine des raies spectrales de l'hydrogène peuvent déjà donner en 1917 une bien meilleure confirmation de la formule de Lorentz-Einstein et ainsi infirmer la théorie d'Abraham[128].
Masse et impulsion relativistes
[modifier | modifier le code]
En 1906, Planck[121] corrige l'erreur dans la définition par Einstein de la masse transverse relativiste, et montre que l'écriture correcte est en accord avec celle publiée par Lorentz en 1899[59]. En même temps, il définit l'impulsion relativiste[129]. À la suite du travail de Planck sur l'impulsion relativiste, Gilbert Lewis en 1908[130] et Richard Tolman en 1912[131] élaborent le concept de masse relativiste, où la masse est définie comme le rapport entre impulsion et vitesse totales, et non comme rapport entre force et accélération (respectivement variations dans le temps de l’impulsion et de la vitesse). Par là, l'ancienne définition de masse longitudinale et transverse devient superflue[132].
Équivalence masse-énergie
[modifier | modifier le code]Einstein en 1906[133] établit que l'inertie de l'énergie (équivalence masse-énergie) est une condition nécessaire et suffisante pour la conservation du mouvement du centre de masse. Il renvoie pour cela à l'article de Poincaré[68] et explique que le contenu de ce travail est fondamentalement en accord avec le sien[69]. Et Kurd von Mosengeil en 1905-1906[134] développe l'hypothèse de Hasenöhrl pour calculer le rayonnement du corps noir à l'intérieur d'une cavité, en considérant la théorie d'Einstein, et pose une fondation importante pour la thermodynamique relativiste — il obtient la même valeur pour la masse du rayonnement électromagnétique que Hasenöhrl. Sur la base du travail de Mosengeil, Planck en 1907[135] peut déduire l'équivalence masse-énergie de l'hypothèse de la cavité, en prenant en compte en plus les forces de liaison de la matière. Il reconnaît la priorité du travail d'Einstein (1905[119]) sur l'équivalence, mais juge sa propre démonstration plus générale[136].
Expériences de Fizeau et de Sagnac
[modifier | modifier le code]Comme il a été mentionné plus haut, Lorentz en 1895[54] a déjà pu expliquer les coefficients d'entraînement de Fresnel et les résultats de l'expérience de Fizeau à partir de la théorie de la lumière en utilisant le temps local, au premier ordre en v / c. Après les premiers essais de Jakob Laub pour établir une « optique des corps en mouvement », c'est Max von Laue en 1907[137] qui démontre cet effet à tous les ordres par une application du théorème d'addition des vitesses relativistes — contrairement à la méthode relativement compliquée de Lorentz. Ce résultat est donc non seulement une confirmation, mais un exemple de l'efficacité et de la simplicité de la relativité restreinte[55].
En 1911, Laue[138] discute d'une expérience possible, où des rayons lumineux sont envoyés dans les deux sens autour d'un banc optique tournant, et reviennent interférer à leur point d'entrée. Son calcul pour un système inertiel, ne tournant pas avec le banc, donne que l’on devrait observer un décalage selon la vitesse de rotation des raies d'interférence, puisque d'après la théorie de la relativité la vitesse de la lumière est indépendante de la vitesse de la source, et ainsi les parcours des rayons pour arriver au point de sortie en mouvement sont différents. Ces parcours seraient différents dans n'importe quel repère inertiel. Une expérience de cette sorte est accomplie par Georges Sagnac en 1913[139], et trouve effectivement ce décalage, c'est l'effet Sagnac. Tandis que Sagnac pense avoir ainsi démontré l'existence d'un éther luminifère au repos, le calcul précédent de Laue montre que l'effet est également en accord avec la relativité — dans les deux théories, la vitesse de la lumière est indépendante de celle de la source. Par contre, un observateur tournant avec le banc optique conclut à des temps de parcours lumineux différents dus à des différences de vitesse, en raison de l'accélération pendant la rotation, ce par quoi l'effet Sagnac peut être considéré comme le pendant optique des effets mécaniques de rotation (comme le pendule de Foucault). La description du point de vue d'un système de référence en rotation sera faite par Paul Langevin en 1937[140], mais dans les systèmes accélérés, la vitesse de la lumière n'est plus constante (voir infra)[141].
Déjà entre 1909 et 1911 une expérience semblable a été faite par Franz Harress, que l'on peut considérer comme une synthèse des expériences de Fizeau et de Sagnac. Il cherche à déterminer le coefficient d'entraînement dans le verre, cependant il utilise un banc tournant, très semblable à celui utilisé plus tard par Sagnac. Il n'interprète pas correctement les déplacements de raie constatés, mais Laue peut montrer plus tard que les résultats de Harress correspondent au résultat de l’expérience de Sagnac[142]. Enfin, l'expérience de Michelson-Gale-Pearson en 1925, une variation de celle de Sagnac, démontre la rotation de la Terre, conformément à la relativité avec un éther au repos[143],[144],[145].
Relativité de la simultanéité
[modifier | modifier le code]Les premières démonstrations de la relativité de la simultanéité par synchronisation au moyen de signaux optiques, dues à Poincaré et Einstein, sont encore simplifiées[146]. En 1910, Daniel Frost Comstock propose de placer au milieu, entre les horloges A et B, un émetteur qui envoie un signal aux deux horloges qui se mettent en marche à la réception du signal. Dans le système au repos de A et B, les horloges se mettent en marche simultanément[n 6]. Dans un système où les horloges se déplacent de B vers A, l'horloge B se met en marche en premier, et A seulement quelque temps après : les horloges ne sont donc pas synchrones dans ce système.
Einstein conçoit aussi en 1917 un modèle avec un récepteur mobile. Dans leur système au repos, les horloges A et B sont synchrones. Au début de l'expérience, le récepteur est au milieu entre A et B, et les horloges envoient un signal. Si le récepteur se déplace vers B, il recevra le signal de B avant celui de A, et dans son système de référence, on juge que les horloges ne sont pas synchronisées[147].
Théorie de l'émission
[modifier | modifier le code]Comme alternative à la relativité, Walther Ritz en 1908[148] et d'autres esquissent une théorie de l'émission qui s'appuie sur la théorie corpusculaire de la lumière de Newton et selon laquelle la vitesse de la lumière dans tous les repères n'est constante que par rapport à la source (et non à quelque éther), et où, au lieu des transformations de Lorentz, on utilise les transformations de Galilée (ce qui veut dire que dans un système où la source se meut avec une vitesse v, la lumière ne se propage pas à la vitesse c, mais à la vitesse ). Cette théorie va donc à l'encontre de la vitesse constante de la lumière, mais elle satisfait au principe de relativité, et peut expliquer l'expérience de Michelson-Morley. Einstein a attiré l'attention avant 1905 sur ce type d'hypothèse[149], ce pourquoi dans ses écrits ultérieurs, il se réfère toujours à l’expérience de Michelson-Morley comme une confirmation du principe de relativité, et non comme une confirmation de la constance de la vitesse de la lumière[150]. En tous cas, une théorie de l’émission nécessiterait une reformulation complète de l'électrodynamique, à l'encontre des succès de la théorie de Maxwell. Finalement la théorie de l'émission passe pour réfutée après la découverte de l'effet Sagnac et les expériences de Willem de Sitter en 1913[151], car une telle théorie devrait donner une contradiction entre l'observation des orbites des étoiles doubles et les lois de Kepler, ce qui n'est pas observé[152]. Des expériences plus récentes avec de la lumière à haute fréquence confirment ce résultat, et les expériences dans les accélérateurs de particules ne peuvent montrer aucune dépendance de la vitesse de la lumière en fonction de celle de la source[153].
Physique de l'espace-temps
[modifier | modifier le code]Espace-temps de Minkowski
[modifier | modifier le code]
L'ansatz quadri-dimensionnel de Poincaré est développé de façon décisive par Hermann Minkowski en 1907 et 1908[154],[155]. Cette géométrisation de la transformation de Lorentz s'appuie par exemple sur les progrès mathématiques réalisés au XIXe siècle, comme la théorie des groupes, la théorie des invariants ou la géométrie projective par des mathématiciens comme Arthur Cayley. Dans un exposé en 1907, Minkowski introduit l’espace-temps comme une « variété non-euclidienne à 4 dimensions »[n 1]. Il arrive à reformuler toute l’électrodynamique par l’introduction d'un formalisme à 4 dimensions dans l'espace nommé en son honneur, espace de Minkowski, ce qui permet une interprétation bien plus claire et cohérente de la relativité restreinte. Il y introduit des concepts comme le temps propre, l'invariance de Lorentz, et utilise des quadrivecteurs, qu'il appelle autrement. Mais sa tentative d'introduire une loi de la gravitation invariante de Lorentz se révèle aussi inefficace que le modèle de Poincaré. Dans son important exposé Raum und Zeit (Espace et temps)[156], où il annonce la fin des représentations précédentes de l'espace et du temps, il introduit le diagramme de Minkowski pour illustrer l'espace-temps.
Minkowski nomme en 1907 ses prédécesseurs dans l'exploitation du principe de relativité : Lorentz, Einstein, Poincaré et Planck. Cependant dans son exposé de 1909, il évoque Voigt, Lorentz et Einstein. Il y critique Lorentz pour le caractère artificiel de son hypothèse de la contraction, là où il considère sa propre interprétation géométrique comme bien plus naturelle. Il loue Einstein pour sa relativisation complète du temps, mais regrette que ni Lorentz ni Einstein n'aient pris complètement en compte la relativité de l’espace. Les revendications de priorité de Minkowski n'ont pas convaincu ses pairs, à quelques exceptions près. Ceci en particulier parce que Minkowski — comme Wien et Abraham — est toujours resté un partisan de la vision électromagnétique du monde, et n'a en apparence pas complètement saisi la différence entre la théorie des électrons de Lorentz et la cinématique d'Einstein[157],[158].
Au début, Einstein et Laub ont renoncé à une formulation quadri-dimensionnelle de la relativité car trop complexe selon eux, et ont publié une démonstration non quadri-dimensionnelle des équations fondamentales pour les corps en mouvement. Cependant, ce sera précisément le formalisme de Minkowski qui sera décisif pour la diffusion et l'acceptation de la relativité restreinte[159].
Notation vectorielle et systèmes clos
[modifier | modifier le code]Il est spécialement significatif que le concept d'espace-temps de Minkowski peut être considérablement raffiné et modernisé sur la forme[158]. Par exemple, Arnold Sommerfeld en 1910[160],[161] remplace la notation matricielle de Minkowski par une notation vectorielle plus élégante, et utilise à ce propos pour la première fois des concepts comme « quadrivecteur » ou « sextivecteur » (ce qui est appelé aujourd'hui tenseur antisymétrique). Il introduit aussi une déduction en trigonométrie hyperbolique de l'addition des vitesses, qui, selon lui, enlève beaucoup à l'aspect bizarre de ce concept. D'autres contributions importantes sont apportées par Von Laue[162],[163], qui généralise les expressions de Minkowski à des processus non électromagnétiques et approfondit ainsi le concept d'équivalence masse-énergie. Von Laue montre aussi que des forces non électriques sont nécessaires pour assurer la validité des propriétés de la transformation de Lorentz et la stabilité de la matière. Ainsi l'électron reste stable — c'est-à-dire qu'il démontre que les contraintes de Poincaré sont une conséquence naturelle de la relativité restreinte afin que l'électron reste un système clos.
Transformations de Lorentz sans postulat sur la vitesse de la lumière
[modifier | modifier le code]Des essais sont faits en vue d'obtenir les transformations de Lorentz sans introduire le postulat de la constance de la vitesse de la lumière. Vladimir Ignatovski[164], par exemple, utilise pour ce faire : a) le principe de relativité, b) l'isotropie et l'homogénéité de l’espace et c) la condition de réciprocité.
En 1910, Philipp Frank et Hermann Rothe[165] montrent alors que cette démonstration est incomplète, et qu'elle repose sur d'autres hypothèses additionnelles, qui n'ont pas été explicitées par Ignatovski. Leur démonstration repose sur les faits que : a) les transformations de Lorentz doivent former un groupe à un paramètre, homogène et linéaire, b) que par échange de systèmes de référence, seul change le signe de la vitesse relative et c) que la contraction des longueurs ne dépend que de la vitesse relative.
Selon Pauli et Miller, Ignatovski tout comme Frank et Rothe ne sont pas en mesure d'identifier la vitesse invariante des transformations obtenues avec la vitesse de la lumière, puisque cette vitesse n'est pas mentionnée dans les postulats. Par exemple, Ignatovski doit revenir à l’électrodynamique pour l'obtenir. Pauli est de l’avis que les deux postulats sont nécessaires pour déduire les transformations de Lorentz[166],[167]. Ceci n'empêche pas certains de rechercher aujourd'hui encore une démonstration des transformations sans utiliser la vitesse de la lumière.
En 1975, Jean-Marc Lévy-Leblond publie un article sur la relativité restreinte présenté sous forme moderne déduite uniquement des propriétés de l'espace et du temps, sans recours à l'électromagnétisme[168]. Le postulat d'Einstein sur l'invariance de la vitesse de la lumière dans tous les référentiels apparaît alors comme une conséquence de la transformation de Lorentz-Poincaré décrivant la relativité restreinte. La transformation de Lorentz-Poincaré fait en effet apparaître une constante de vitesse qui s'apparente à une vitesse limite. Et c'est cette limite mathématique qui est prise pertinemment égale à la vitesse c de la lumière dans le vide. En 2005, Jean Hladik reprend cette approche dans un livre de vulgarisation[169].
Reformulations non-euclidiennes de la théorie
[modifier | modifier le code]
Minkowski établit en 1907 que le formalisme d'espace-temps possède un lien étroit avec la géométrie hyperbolique[n 1]. Cependant, il continue à utiliser une coordonnée de temps imaginaire comme quatrième dimension[170]. De même dans le travail de Born[171] sur l'accélération de corps rigides, il apparaît des analogies avec la géométrie riemannienne[172], ce qui est pour Einstein, en liaison avec le paradoxe d'Ehrenfest, un indice important pour sa future théorie de la gravitation[n 1]. Des essais systématiques sont alors entrepris par divers mathématiciens et physiciens pour reformuler l'ensemble de la relativité restreinte sur la base d'une géométrie pseudo-euclidienne, avec une coordonnée de temps réelle comme quatrième dimension. Les connaissances ainsi acquises permettent des formulations élégantes des diverses expressions de la théorie. Mais au fond, ces modèles plus maniables sur le plan mathématique ne vont pas plus loin que la relativité restreinte, en ce qui concerne le contenu physique. En 1911 et 1912, Vladimir Varićak[173],[174] remarque l'analogie avec la géométrie hyperbolique et tente de reformuler la relativité sur cette base. En 1911, Alfred Robb[175] introduit le concept de rapidité
qui est le paramètre du groupe de Lorentz écrit sous forme additive. En 1912, Edwin Bidwell Wilson et Gilbert Lewis[176] utilisent un calcul vectoriel pseudo-euclidien[n 1]. Émile Borel en 1913[177] pose les bases cinématiques de la précession de Thomas en utilisant la géométrie hyperbolique. Cependant, le formalisme originel de Minkowski d'espace-temps restera longtemps préféré[170], et la géométrie pseudo-euclidienne attendra le développement de la relativité générale pour jouer un rôle important en physique. Au début du XXIe siècle, dans la plupart des travaux sur la relativité restreinte, les scientifiques préfèrent la représentation pseudo-euclidienne avec toutes les coordonnées réelles.
Dilatation du temps et paradoxe des jumeaux
[modifier | modifier le code]En 1907, Einstein[178] montre que l'effet Doppler transversal (qui est une conséquence de la dilatation du temps) donne la possibilité de vérifier expérimentalement la dilatation du temps. En 1938, Herbert Eugene Ives et G. R. Stilwell réussiront à démontrer expérimentalement cet effet, et donc la dilatation du temps par l'expérience d'Ives-Stilwell[179].
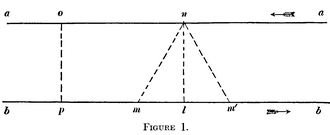
Lewis et Tolman en 1909[180] illustrent la réciprocité de la dilatation du temps exigée par Einstein par l'utilisation de deux horloges à lumière A et B identiques, qui se rapprochent l'une de l'autre avec une certaine vitesse relative. Les horloges consistent en deux miroirs parallèles à leur mouvement relatif se renvoyant un signal lumineux. Pour un observateur immobile par rapport à A, la période de son horloge est le temps d'un aller-retour entre les deux miroirs. Quand il regarde l'horloge B, il remarque que le temps de parcours est plus long, car le rayon doit se propager en oblique pour atteindre l'autre miroir qui a avancé. La période de B lui paraît donc plus longue que celle de A. Pour un observateur situé au repos par rapport à B, la situation est inversée : B est au repos, A bouge et va donc plus lentement que B. Dans un exposé entre 1910 et 1912, Lorentz discute aussi la réciprocité de la dilatation du temps et le paradoxe des horloges qui semble aller avec. Lorentz montre que le fait de dire que chacun voit l'horloge de l’autre aller plus lentement n'est pas un paradoxe. On doit simplement penser que dans un système, on ne mesure qu'avec une horloge, mais que pour comparer les deux cas, il faut deux horloges, et dans ce cas on doit mettre en cause la relativité de la simultanéité.
En 1911, Paul Langevin[181] poursuit en créant une situation semblable, le paradoxe des jumeaux, célèbre en physique, en remplaçant les horloges par des personnes[n 7], dont l'une reste immobile, et l'autre accomplit un long voyage rapide aller-retour. À son retour, le voyageur se trouve moins vieilli que le sédentaire. Langevin résout le paradoxe en remarquant l'asymétrie des deux observateurs : pour le voyageur, un changement complet de direction a lieu sous l'action de l'accélération. Mais Langevin considère cela comme une indication de « mouvement absolu » dans un éther. Quoique l'explication d'asymétrie soit conservée jusqu'à présent, la conclusion sur l'éther est abandonnée. Par exemple Max von Laue en 1913[182] indique que peu importe la durée de l'accélération, ce qui compte est le fait que le jumeau voyageur se trouve successivement dans deux systèmes inertiels différents, tandis que le jumeau immobile reste toujours dans le même système. Laue est aussi le premier à illustrer le problème avec des diagrammes de Minkowski, et à établir que la ligne d'univers d'un observateur en mouvement inertiel maximise le temps propre entre deux événements dans l'espace-temps[183].
Accélération
[modifier | modifier le code]En 1909, Einstein[184] essaie de prendre en compte également les mouvements quelconques (accélérés) dans le cadre du principe de relativité. Il reconnaît qu'on peut définir pour chaque segment de la trajectoire d'un point dans l'espace-temps un système inertiel où le point se trouve au repos. Pour chaque petit segment, on peut prendre pour coordonnées de l'espace-temps celles du système inertiel ainsi défini. Avec l'ensemble de ces coordonnées, on définit ainsi un système de référence accéléré, où l'on ne peut plus appliquer le principe de constance de la vitesse que localement. Dans cette circonstance, le principe d'équivalence formulé par Einstein, et qui affirme que les masses grave[n 8] et inerte sont égales, et que les processus dans un système de référence uniformément accéléré sont équivalents à des processus dans un champ de gravitation homogène, fait « exploser » les limites de la relativité restreinte et fraie la voie à la relativité générale.
Presque en même temps qu'Einstein, Minkowski[155] traite le cas particulier d'une accélération uniforme dans le cadre de son formalisme d'espace-temps, et découvre que la ligne d'univers correspondante est une hyperbole. Ceci est poursuivi par Born en 1909[171] et Sommerfeld en 1910[161], et Born crée pour ce phénomène l'expression « mouvement hyperbolique ». Il reconnaît à nouveau que l'accélération uniforme peut être utilisée comme approximation locale pour la description de diverses accélérations en relativité restreinte.
Par ailleurs, tous les deux en 1909, Harry Bateman[185] et Ebenezer Cunningham[186], démontrent que les équations de Maxwell sont invariantes non seulement sous le groupe de Lorentz, mais sous un groupe plus général de transformations conformes, et par conséquent conservent leurs propriétés pour tout un ensemble de mouvements accélérés. Une formulation covariante de l’électrodynamique est donnée finalement par Friedrich Kottler[187]. Elle restera valable dans le cadre de la relativité générale qui sera développée plus tard. En ce qui concerne les développements sur la description de l'accélération dans le cadre de la relativité restreinte, il faut citer notamment les travaux de Paul Langevin sur les systèmes de référence en rotation, et surtout ceux de Wolfgang Rindler[188],[189].
Corps rigides et réalité de la contraction des longueurs
[modifier | modifier le code]En 1907, Einstein[190] se demande si, surtout par exemple dans les corps rigides, l'information peut se propager plus vite que la lumière. Il explique que dans de telles circonstances, il serait possible d'envoyer des informations vers le passé, et de violer la causalité. Comme ceci s'oppose à toute expérience, il est exclu d'avoir des vitesses supérieures à celle de la lumière. Il ajoute qu'il faut donc établir une dynamique des corps rigides en relativité restreinte[n 9]. Quand Born en 1909[171] essaie d'étendre la relativité aussi aux mouvements accélérés, il utilise le concept de corps rigide. Mais ce modèle débouche sur une impasse théorique, car Paul Ehrenfest[191] publie un court travail dans lequel il montre qu'un corps rigide ne peut pas être mis en rotation dans le cadre de la relativité restreinte, car son périmètre devrait diminuer en raison de la contraction des longueurs, à rayon constant. C'est le paradoxe d'Ehrenfest. Ces études sont poursuivies notamment par Gustav Herglotz et Fritz Noether, qui développent une théorie relativiste de l'élasticité, et doivent y restreindre considérablement la notion de « corps rigide ». Finalement, Max von Laue en 1911[138] montre qu'en relativité, un corps doit avoir une infinité de degrés de liberté, c'est-à-dire qu'il n’existe absolument aucun corps « rigide ». Alors que la définition de Born du référentiel en rotation pour des corps rigides physiques n'est plus tenable, elle reste tout à fait utilisable pour la description de la cinématique des mouvements de rotation. Cependant, ce genre d'expérience de pensée est un indice important pour la théorie de la gravitation qu'Einstein doit encore élaborer, parce qu'il reconnaît que la géométrie dans un système tournant n’apparaît pas comme euclidienne — bien que la géométrie intrinsèque de l'espace ne dépende pas du choix des coordonnées.
La description qui reste adéquate jusqu’à présent de la description d'un système de référence tournant sera celle de Langevin[192], pour laquelle, en raison de la complexité des relations (et souvent du fait qu'on ne sait pas les résoudre), diverses variations et extensions ont été publiées depuis[188].
En relation avec le paradoxe d'Ehrenfest, Varićak en 1911[173] demande si la contraction des longueurs est « réelle » ou « apparente ». Il s'agit ici d'une querelle sémantique, car comme Einstein le fait remarquer dans sa réponse à Varićak, la contraction des longueurs est apparente, puisqu'elle n’existe pas pour un observateur au repos par rapport à l'objet considéré, mais elle est néanmoins mesurable pour un observateur mobile[193]. La différence entre contraction de Lorentz et relativité gît dans l'interprétation : pour Einstein, la contraction n'est qu'un effet cinématique dû aux instants de mesure par l'observateur des extrémités (non synchrones dans le système au repos de l'objet), tandis que pour Lorentz, il s'agirait d'un effet mécanique dynamique dû à des forces transmises par l’éther.
Gravitation
[modifier | modifier le code]La première tentative de formulation d'une théorie relativiste de la gravitation est entreprise par Poincaré en 1905[194]. Il s'efforce de modifier la loi de gravitation de Newton en sorte que la loi résultante prenne une forme covariante de Lorentz. Il remarque que sa solution n'est pas unique, et que d'autres solutions sont possibles. Cependant, il réussit à contourner l'objection faite vers 1800 par Pierre-Simon de Laplace, selon laquelle la vitesse de propagation de la gravitation doit être bien plus élevée que celle de la lumière, en raison de l'aberration gravitationnelle, qui rendrait les orbites instables. Poincaré montre au contraire que dans une théorie covariante de Lorentz, la propagation se fait à la vitesse de la lumière, et que des orbites stables sont néanmoins possibles[n 10]. Des modèles semblables ont été présentés à la suite de celui de Poincaré par Minkowski en 1908[155] et par Sommerfeld en 1910[160],[161].
Mais Abraham en 1914[195] montre que pratiquement tous les modèles « mécaniques » de la gravitation, comme celui de Le Sage, ou ceux de Poincaré et de Minkowski, appartiennent à la classe des « théories vectorielles ». Celles-ci ont l'inconvénient fondamental que l'énergie du champ de gravité doit prendre une valeur négative, et que l'on ne peut pas garantir le principe de la conservation de l'énergie. Abraham et Gustav Mie proposent diverses « théories scalaires » comme alternatives. Alors que Mie ne peut jamais formuler sa théorie complètement sans contradiction, Abraham (qui est resté toute sa vie un adversaire de la relativité) développe une théorie dans laquelle la vitesse de la lumière n'est plus constante, même localement, et ainsi n’est plus compatible avec les principes de base de la relativité.
En outre, toutes ces théories violent une condition (principe d'équivalence) qu'Einstein a proposée en 1907 : l'égalité entre masse inerte et masse grave[n 8]. Einstein croit alors qu'il est impossible de développer une théorie qui satisfasse à la fois la covariance de Lorentz et le principe d'équivalence. Cependant Gunnar Nordström en 1913[196] réussit à développer une théorie scalaire de la gravitation, dans laquelle les deux conditions sont remplies. Mais il y arrive en faisant dépendre aussi bien la masse inerte que la masse grave du potentiel gravitationnel. Sa théorie est en outre d'autant plus remarquable que (comme l'ont montré Einstein et Adriaan Fokker en 1914), pour la première fois, les effets gravitationnels peuvent être représentés complètement par la géométrie d'un espace-temps courbe. Bien que la théorie de Nordström soit sans contradiction, elle souffre du point de vue d'Einstein du problème suivant : elle ne satisfait pas la covariance, qu'il considère comme particulièrement importante, car des systèmes de référence préférentiels peuvent y être définis. À l'opposé de ces théories scalaires en accord avec la relativité restreinte, Einstein travaille alors à une « théorie tensorielle » de la gravitation (1911-1915), qui doit aussi bien satisfaire le principe d'équivalence que décrire les mouvements les plus divers (y compris accélérés) d'une manière généralement covariante. Cette théorie (qu'Einstein[197] nomme « relativité générale ») fait « sauter » les limites de la relativité restreinte et de la covariance de Lorentz, car le principe de la constance de la vitesse de la lumière ne devient plus valable que localement[198]. La différence entre les théories covariantes de Lorentz et la relativité générale fournit pour la première fois l'explication d'un phénomène qui a été évoqué dans beaucoup de travaux sur la gravitation, sans être considéré comme décisif : la précession du périhélie de Mercure, qui est alors totalement expliquée par la relativité générale. En outre, c'est la seule (par opposition aux théories covariantes de Lorentz) à fournir la bonne valeur pour la déviation de la lumière par le Soleil[199],[200].
Acceptation de la théorie
[modifier | modifier le code]Finalement, la différence entre les théories de Lorentz et d'Einstein, sur le plan philosophique et de l’interprétation, finit par se cristalliser. On n'utilise plus le terme « théorie de Lorentz-Einstein », et presque plus personne ne reconnaît l'existence d'un éther sous quelque forme que ce soit (à part des exceptions comme Lorentz, Poincaré et Langevin). C'est ainsi que Planck dès 1909 compare les conséquences du principe moderne de la relativité — et avant tout celles de la relativité du temps, d'Einstein — avec la révolution copernicienne de la conception du monde[201]. Le plus significatif est aussi que le concept d'espace-temps de Minkowski a été formellement considérablement affiné et modernisé, ce qui contribue à une large acceptation de la relativité restreinte par les physiciens et les mathématiciens[158]. C'est en 1911 que Laue publie sa première monographie sur la relativité restreinte, Sommerfeld décrit la relativité restreinte comme une des bases sûres de la physique, et Wien propose en 1912 Lorentz et Einstein ensemble pour le prix Nobel de physique en raison de leurs performances pour l'élaboration du principe de la relativité. Einstein est déjà à cette époque très occupé à construire la relativité générale, en montrant (voir supra) que la relativité restreinte ne suffit pas pour développer une théorie de la gravitation en accord avec les observations[n 9].
Critiques
[modifier | modifier le code]Un certain nombre de scientifiques, de philosophes et d'intellectuels ont repoussé, et repoussent encore, la relativité. Ce rejet s'appuie sur des considérations scientifiques, pseudo-scientifiques, philosophiques ou idéologiques. Par exemple, Henri Bergson, « le plus prestigieux philosophe français de l'époque », publie en 1922 son ouvrage Durée et Simultanéité qui tente de « réfuter les idées d'Einstein »[202]. Cependant, les scientifiques contemporains, à une très large majorité, reconnaissent que la théorie est suffisamment vérifiée par de nombreuses expériences et qu'elle est cohérente.
Priorités
[modifier | modifier le code]Les rôles des divers acteurs dans le développement de la relativité restreinte ont été extrêmement entremêlés, et il est toujours difficile en sciences de définir comment une idée a germé, crû et mûri. Divers acteurs contribuent en général à cette croissance. Les historiens des sciences accordent plus ou moins de poids aux contributions des uns et des autres, pour des raisons souvent justifiées dans une certaine logique, parfois plus subjectives.
Ainsi, par exemple, Edmund Taylor Whittaker[203] ou Logunov[204] parlent de la création de Poincaré et de Lorentz, tout en minimisant le rôle d'Einstein. Ce n'est pas l'opinion de la majorité des spécialistes, comme Gerald Holton[205], Arthur I. Miller[10], Abraham Pais[206] ou John Stachel[207],[208], qui reconnaissent les prouesses de Poincaré, mais soulignent qu'Einstein est le premier à enseigner la relativisation complète de l'espace-temps, en éliminant l'éther de la physique.
Lorentz
[modifier | modifier le code]Bien que partisan de la notion d'éther, Lorentz[209], dans son ouvrage majeur La Théorie des électrons, admet les qualités du « principe de relativité d'Einstein » et de son application aux horloges, longueurs et synchronisation. La prouesse d'Einstein est d'avoir remplacé son formalisme bien plus lourd par une équivalence complète entre référentiels, notamment de la variable « temps ». Le nom de Poincaré n'apparaît dans aucune des deux éditions[210]. En revanche, dans un article de 1915 publié en 1921[211], Lorentz loue Poincaré pour avoir, en 1905-1906, correctement interprété le temps local comme celui de l'observateur, alors qu'il ne le considérait lui-même que comme un artifice mathématique heuristique. C'est la seule fois où il le cite, et il attribue ailleurs tout le mérite de la relativité à Einstein.
Poincaré
[modifier | modifier le code]Poincaré présente toujours les nouvelles théories comme étant des créations de Lorentz, et ne voit aucune raison de citer Einstein ou Minkowski dans ce contexte[212]. Ainsi, en 1912, peu avant sa mort, il écrit au sujet de la permanence de la « mécanique de Lorentz » après le développement de la théorie des quanta :
Bien que Poincaré souligne dans ses écrits philosophiques la relativité du temps, ses travaux de physique[68],[106],[214],[215] réfèrent à un éther (non découvrable). Il répartit ainsi les coordonnées et les phénomènes selon leur caractère local/apparent pour l’observateur en mouvement ou vrai/réel pour l’observateur au repos par rapport à l'éther[216],[91]. Ceci explique que la majorité des historiens pensent que la théorie de Poincaré ne correspond pas à ce que nous appelons aujourd'hui la relativité, malgré de nombreuses contributions sur la méthode et les résultats.
Einstein
[modifier | modifier le code]Le travail d'Einstein de 1905[116] sur l'électrodynamique ne contient aucune référence à d'autres travaux. C'est pourquoi les biographes d'Einstein, Abraham Pais[217] et Albrecht Fölsing[218], attirent l'attention sur la citation suivante d'Einstein, à propos de la réception de ses œuvres[219] :
Dans une lettre à Stark de 1907, Einstein écrit qu'en raison de son activité dans le bureau de brevets où il travaille, il n'a que très peu d'occasions d'aller en bibliothèque pour étudier à fond la littérature spécialisée. Ceci ne signifie pas qu'il soit étranger au statut général de la science, mais ce n'est que dans certains domaines qu'il est parfaitement informé[218],[220].
Certains historiens des sciences essaient encore d'inventorier les sources possibles d'Einstein. Le gros de ses informations proviendrait d'articles importants de Wien, Cohn, Abraham, Bucherer ou Hasenöhrl dans les Annalen der Physik, où il a publié plusieurs articles, ainsi que des critiques d'articles dans les Beiblätter, principalement en thermodynamique. En outre, par son activité d'expert dans un bureau de brevets, il peut s'atteler au problème de la synchronisation des horloges au moyen de signaux électriques se propageant à vitesse finie, problème lié à l'époque au développement des chemins de fer et à la maîtrise de leur circulation. Il connaît aussi le travail de Lorentz de 1895[54], qui décrit le temps local, la contraction des longueurs et l'expérience de Michelson-Morley[221].
Même si l'idée fondamentale de la constance de la vitesse de la lumière vient du concept d'éther de Lorentz, il parvient, contrairement à Lorentz et à Poincaré, au fait que l'équivalence des référentiels et l'indétectabilité de l'éther rendent superflue l'idée même de l'éther[149].
Cependant, en 1955, il écrit à Carl Seelig[221] :
Notes et références
[modifier | modifier le code]- (de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Geschichte der speziellen Relativitätstheorie » (voir la liste des auteurs).
Notes
[modifier | modifier le code]- L'expression « non-euclidien » peut être prise dans plusieurs acceptions. L'une d'entre elles correspond à la géométrie d'espaces courbes, où le postulat des parallèles n'est plus satisfait, comme la géométrie de Riemann ou de Lobatchevsky. Une autre correspond, comme celle de Minkowski, à un espace plat, où le postulat des parallèles est satisfait, mais où il existe deux sortes d'intervalles dont la longueur au carré n'est pas forcément positive, ce qui conduit Minkowski à prendre des coordonnées réelles et une coordonnée imaginaire. On appellera ce type d'espace, pour préciser, « espace pseudo-euclidien ». Enfin, Einstein introduira dans sa relativité générale un espace à la fois courbe et avec des carrés de longueurs des deux signes, ce sera un espace « pseudo-riemannien ».
- Sur la question de l'antécédence des travaux d'Einstein et de Poincaré, voir Controverse sur la paternité de la relativité.
- Et d'une quantité d'autres expériences faites jusqu'alors. Voir (en) Tom Roberts, Siegmar Schleif et John M. Dlugosz, What is the experimental basis of Special Relativity?, Physics FAQ, (lire en ligne)
- Le condensateur circulaire centré sur la source crée le champ électrique (voir supra). Il a des électrodes très rapprochées (0,25 mm) pour un rayon de 4 cm, ce qui sélectionne pour chaque direction α par rapport au champ magnétique la vitesse d'électrons susceptible de les maintenir entre les électrodes sous l'influence des champs électrique et magnétique croisés. Une fois sorti du condensateur, l'électron est uniquement soumis au champ magnétique, et donc dévié perpendiculairement à lui. La trace du faisceau sur le film cylindrique entourant le condensateur à 4 cm permet de remonter directement à la dépendance du rapport charge/masse en fonction de la vitesse, via α.
- L'appareil utilisé par Hippolyte Fizeau est beaucoup plus complexe, la source lumineuse émet en continu et la distance entre le miroir et la roue dentelée est beaucoup plus grande, mais l'explication qui suit est valable (Serway 1992, p. 151-152).
- (en)« Most people will, I think, agree that one of the very best practical and simple ways would be to send a signal to each point from a point half-way between them. The velocity with which signals travel through space is of course the characteristic "space velocity," the velocity of light. Two clocks, one at A and the other at B, can therefore be set running in unison by means of a light signal sent to each from a place midway between them » (Comstock 1910, p. 768).
- Il n'a pas explicitement mentionné des jumeaux, mais sa présentation contient tous les autres caractères du paradoxe.
- On appelle « masse inerte » le rapport de la force à l'accélération ; la « masse grave » est celle qui intervient dans la formule d'attraction universelle de la gravitation de Newton.
- C'est en 1907, pour la première fois, qu'Einstein utilise comme Planck et Bucherer, l'expression « théorie de la relativité ». Ce sera en 1915 qu'il utilisera pour la première fois l'expression « relativité restreinte » pour faire la différence entre cette théorie et la « relativité générale » qu'il met au point.
- À condition, toutefois, de négliger le très faible rayonnement d'ondes gravitationnelles, qui fait très lentement perdre de l'énergie au corps en orbite. Ce phénomène n'a encore été observé qu'à proximité des trous noirs.
- (de)« 'Es ist zweifellos, daß die spezielle Relativitätstheorie, wenn wir ihre Entwicklung rückschauend betrachten, im Jahre 1905 reif zur Entdeckung war. LORENTZ hatte schon erkannt, daß für die Analyse der MAXWELLSchen Gleichungen die später nach ihm benannte Transformation wesentlich sei, und POINCARE hat diese Erkenntnis noch vertieft. Was mich betrifft, so kannte ich nur LORENTZ bedeutendes Werk von 1895 "La theorie electromagnetique de MAXWELL" und "Versuch einer Theorie der elektrischen und optischen Erscheinungenin bewegten Körpern" - aber nicht LORENTZ', spätere Arbeiten, und auch nicht die daran anschließende Untersuchung von POINGARE. In diesem Sinne war meine Arbeit von 1905 selbständig. »
Références
[modifier | modifier le code]- Boucher 2008, p. 255
- Isaac McPhee (trad. de l'anglais par Corinne Chevallard), La Physique au lit [« The Bedside Book of physics »], Paris, Belin, coll. « Petit précis à déguster », , 176 p. (ISBN 978-2-7011-5958-4), p. 54
- Voir par exemple DiSalle 2002.
- Pour l'espace : « Newton therefore held that physics required the conception of absolute space, a distinguished frame of reference relative to which bodies could be said to be truly moving or truly at rest. »
- Pour le temps « Yet [Euler] noted that the laws of motion permit us to determine, not the velocity of any motion in space, but only the absolute sameness of direction of an inertial trajectory over time, and the equality of time-intervals in which an inertially-moving particle moves equal distances. »
- Newton 1759 en p. 52 écrit « Pour les éviter, il faut distinguer le temps, l’espace, le lieu, et le mouvement, en absolus et relatifs, vrais et apparents, mathématiques et vulgaires.
I. Le temps absolu, vrai et mathématique, sans relation à rien d’extérieur, coule uniformément, et s’appelle durée. Le temps relatif, apparent et vulgaire, est cette mesure sensible et externe d’une partie de durée quelconque (égale ou inégale) prise du mouvement : telles sont les mesures d’heures, de jours, de mois, et c’est ce dont on se sert ordinairement à la place du temps vrai.
II. L’espace absolu, sans relation aux choses externes, demeure toujours similaire et immobile. » - Moulaye Ahmed 2007, p. 63
- Hentschel 1990, p. 4 sq.
- Hentschel 1990, p. 5 sq.
- Hentschel 1990, p. 10
- Katzir 2005
- Miller 1981
- Pais 1982, chap. 7
- Minkowski 1907
- Fresnel 1816
- Whittaker 1951, p. 128 sq.
- Maxwell 1864
- Whittaker 1951, p. 240 sq.
- Maxwell 1873
- Bartoli 1876
- Whittaker 1951, p. 271 sq.
- Heaviside 1889
- Hertz 1890a
- Hertz 1890b
- Whittaker 1951, p. 319 sq.
- Janssen et Stachel 2004, p. 20
- Miller 1981, p. 46
- Fresnel 1866 en p. 249 écrit « [...] la lumière résultait des vibrations d'un fluide universel extrêmement subtil, agité par les mouvements rapides des corps des luminuex, de la même façon que l'air est ébranlé par les vibrations des corps sonores » ; en p. 250, il écrit « Sous ce rapport, le système qui fait consister la lumière dans les vibrations d'un fluide universel, a de grands avantages sur celui de l'émission [de particules]. » et en p. 282, il écrit « En admettant que la lumière consiste dans des vibrations de l'éther [...] »
- Lorentz 1892a, p. 6
- Whittaker 1951, p. 107 sq.
- Stokes 1845
- Whittaker 1951, p. 386 sq.
- Fizeau 1851
- Janssen et Stachel 2004, p. 4–15
- Michelson 1881
- Whittaker 1951, p. 390 sq.
- Lorentz 1886
- Michelson et Morley 1886
- Janssen et Stachel 2004, p. 18–19
- Janssen et Stachel 2004, p. 19-20
- Voigt 1887
- Ernst et Hsu 2001
- Miller 1981, p. 114–115
- Pais 1982, chap. 6b
- Lorentz 1909
- Lorentz 1909, p. 198 écrit sur le sujet dans la note de bas de page : « In a paper `Über das Dopplersche Prinzip' published in 1887 (Gött. Nachrichten p. 41) ... Voigt has applied to equations of the form 6 (§ 3 of this book) a transformation equivalent to the formulae (287) and (288) [NdT : à savoir la transformation de Lorentz]. The idea of the transformation used above (and in § 44) might therefore have been borrowed from Voigt and the proof that it does not alter the form of the equation for the free ether in his paper. »
- (de) Emil Kohl, « Über ein Integral der Gleichungen für die Wellenbewegung, welches dem Dopplerschen Prinzipe entspricht », Annalen der Physik, vol. 11, no 5, , p. 96-113
- (en) Charles Kittel, « Larmor and the Prehistory of the Lorentz Transformation », American Journal of Physics, vol. 42, , p. 726-729
- Searle 1897
- Miller 1981, p. 99–100
- FitzGerald 1889
- Brown 2001
- Lorentz 1892b
- Miller 1981, p. 27–29
- Janssen 1995, chap. 3.3
- Lorentz 1895
- Janssen 1995, chap. 3.1
- Larmor 1897
- Larmor 1900
- Macrossan 1986
- Lorentz 1899
- Janssen et Stachel 2004, p. 31–32
- Thomson 1881
- Whittaker 1951, p. 306 sq.
- Whittaker 1953, p. 51 sq.
- Heaviside 1888
- Janssen 1995, chap. 3.4
- Wien 1900
- Miller 1981, p. 46, 103
- Poincaré 1900b
- Darrigol 2005, p. 18–21
- Kaufmann 1902
- Kaufmann 1905
- Miller 1981, p. 47–54, 61–67
- Abraham 1902
- Abraham 1903
- Miller 1981, p. 55–61
- Hasenöhrl 1904
- Hasenöhrl 1905
- Miller 1981, p. 359–360
- Giulini 2001, chap. 4
- DiSalle 2002
- Neumann 1870
- Mach 1883
- Streintz 1883
- Lange 1885
- Poincaré 1902
- Archibald 1914
- Goenner 2008
- Gibson et Ralph 1928
- Hentschel 1990, p. 153-154
- Poincaré 1898
- Galison 2003
- Poincaré 1895
- Poincaré 1900a
- Katzir 2005, p. 272–275
- Darrigol 2005, p. 10–11
- Bucherer 1903
- Darrigol 2000, p. 369-372
- Lorentz 1904b
- Janssen 1995, chap. 3.3, 3.4
- Wien 1904a
- Wien 1904b
- Miller 1981, chap. 1, note 57
- Abraham 1904
- Miller 1981, chap. 1.13
- Miller 1981, p. 75–79
- Poincaré 1904
- Katzir 2005, p. 275–277
- Cohn 1904
- Miller 1981, p. 79–86
- Henri Poincaré et Scott A. Walter (éditeur), La correspondance entre Henri Poincaré et les physiciens, chimistes, et ingénieurs, Bâle, Birkhäuser, (lire en ligne), « 38.3, Poincaré to Lorentz, Mai 1905 », p. 255–257
- Henri Poincaré et Scott A. Walter (éditeur), La correspondance entre Henri Poincaré et les physiciens, chimistes, et ingénieurs, Bâle, Birkhäuser, , 257–258 p. (lire en ligne), « 38.4, Poincaré to Lorentz, Mai 1905 »
- Katzir 2005, p. 280–288
- Pais 1982, chap. 6c
- Walter 2007, chap. 1
- Voir par exemple :
- (en) Albert Einstein et John Stachel (préf. Roger Penrose), Einstein's Miraculous Year : Five Papers that Changed the Face of Physics, Princeton (New Jersey), Princeton University Press, , 248 p. (ISBN 978-0-691-12228-1, présentation en ligne)
« The anno mirabilis was 1905, when an obscure patent examiner published several papers. This volume consists of translations of Einstein's revolutionary papers that year [...] »
- ____, « Relativité », dans Temps, matière & espace, les 150 choses à savoir, Science & Vie, coll. « Hors série » (no 260), , p. 88
- Einstein 1905a
- Darrigol 2005, p. 15–18
- Janssen 1995, chap. 4
- Einstein 1905b
- Kaufmann 1906
- Planck 1906a
- Planck 1906b
- Einstein 1908a
- Miller 1981, p. 88
- Miller 1981, p. 334–352
- Bucherer 1908
- Neumann 1914
- Pauli 1921, p. 636–637
- Miller 1981, p. 329–330
- Lewis 1908
- Tolman 1912
- Pauli 1921, p. 634–636
- Einstein 1906
- Mosengeil 1907
- Planck 1907
- Miller 1981, p. 359–367
- Laue 1907
- Laue 1911b
- Sagnac 1913
- Langevin 1937
- Laue 1921, p. 25, 146-148
- Laue 1921, p. 25-26, 204-206
- (de) Georg Joos, Lehrbuch der theoretischen Physik, Akademische Verlagsgesellschaft Geest & Portig, , 842 p. (présentation en ligne), p. 448.
- (en) A. A. Michelson, « The Effect of the Earth's Rotation on the Velocity of Light, I. », Astrophysical Journal, vol. 61, , p. 137 (DOI 10.1086/142878, résumé, lire en ligne)
- (en) A. A. Michelson et Henry G. Gale, « The Effect of the Earth's Rotation on the Velocity of Light, II. », Astrophysical Journal, vol. 61, , p. 140 (DOI 10.1086/142879, résumé, lire en ligne)
- Bjerknes 2002
- (en) Albert Einstein (trad. Robert William Lawson), Relativity : The Special and the General Theory, (lire en ligne), chap. 9 (« Section 9 - The Relativity of Simultaneity »)
- Ritz 1908
- Norton 2004
- Stachel 1982
- De Sitter 1913a
- Pauli 1921, p. 549–553
- Born 1964, p. 326–333
- Minkowski 1907
- Minkowski 1908
- Minkowski 1909
- Miller 1981, chap. 7.4.6
- Walter 1999a, chap. 3
- Walter 1999a, p. 49
- Sommerfeld 1910a
- Sommerfeld 1910b
- Miller 1981, chap. 12.5.8
- Janssen et Mecklenburg 2007
- Ignatovski 1910
- Frank et Rothe 1910
- Pauli 1921, p. 555–556
- Miller 1981, p. 218–219
- (en) Jean‐Marc Lévy‐Leblond, « One more derivation of the Lorentz transformation », American Journal of Physics, vol. 44, no 3, , p. 271–277 (ISSN 0002-9505, DOI 10.1119/1.10490)
- Jean Hladik, Pour comprendre simplement la théorie de la Relativité, Ellipses, , 142 p. (ISBN 9782729823023)
- Walter 1999b
- Born 1909
- Pais 1982, chap. 12b
- Varićak 1911
- Varićak 1912
- Robb 1911
- Lewis et Wilson 1912
- Borel 1913b
- Einstein 1907a
- Miller 1981, p. 245–253
- Lewis et Tolman 1909
- Langevin 1911
- Laue 1913
- Miller 1981, p. 257–264
- Einstein 1909
- Bateman 1909
- Cunningham 1909
- Kottler 1912
- Pauli 1921, p. 690–691
- Rindler 2001
- Einstein 1907b
- Ehrenfest 1909
- Langevin 1935
- Pauli 1921, p. 556–557
- Poincaré 1905b
- Abraham 1914
- Nordström 1913
- Einstein 1916
- (en) Philip Gibbs et Steve Carlip, « Is the Speed of Light Constant ? », Usenet Physics FAQ, (consulté le )
- Norton 2005
- Walter 2007
- Pais 1982, p. 11a
- Boucher 2008, p. 269
- Whittaker 1953, p. 27 sq.
- Logunov 2004
- Holton 1973
- Pais 1982
- Stachel 1982
- Stachel 2002
- Lorentz 1910
- Janssen 1995, chap. 3.5.4
- Lorentz 1915
- Miller 1981, p. 255
- Poincaré 1913, p. 166
- Poincaré 1906
- Poincaré 1908
- Miller 1981, p. 216-217
- Pais 1982, chap. 8
- Fölsing 1993, chap. 7
- Einstein 1907b, p. 373
- Miller 1981, chap. 1.15
- Born 1956, p. 193
Annexes
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]Note : La Wikisource en anglais propose une longue liste d'articles touchant l'histoire de la relativité restreinte.
Sources primaires
[modifier | modifier le code]- (de) Max Abraham, « Dynamik des Elektrons », Nachr. Ges. Wiss. Göttingen, Mathematisch-Physikalische Klasse, , p. 20-41
- (de) Max Abraham, « Prinzipien der Dynamik des Elektrons », Annalen der Physik, vol. 315, no 1, , p. 105-179
- (de) Max Abraham, « Die Grundhypothesen der Elektronentheorie », Physikalische Zeitschrift, vol. 5, , p. 576-579
- (de) Max Abraham, « Neuere Gravitationstheorien », Jahrbuch für Radioaktivität und Elektronik, vol. 11, no 4, , p. 470-520
- (en) R.C. Archibald, « Time as a fourth dimension », Bull. Amer. Math. Soc., vol. 20, , p. 409-412
- (it) Adolfo Bartoli, « Il calorico raggiante e il secondo principio di termodynamica », Il Nuovo Cimento, vol. 15, , p. 196-202
- (en) Harry Bateman, « The Transformation of the Electrodynamical Equations », Proceedings of the London Mathematical Society, vol. 8, , p. 223-264
- Émile Borel, « La théorie de la relativité et la cinématique », Comptes Rendus des séances de l’Académie des Sciences, vol. 156, 1913a, p. 215-218
- Émile Borel, « La cinématique dans la théorie de la relativité », Comptes Rendus des séances de l’Académie des Sciences, vol. 157, 1913b, p. 703-705
- (de) Max Born, « Die Theorie des starren Körpers in der Kinematik des Relativitätsprinzips », Annalen der Physik, vol. 335, no 11, , p. 1-56
- (de) Alfred Heinrich Bucherer, « Über den Einfluß der Erdbewegung auf die Intensität des Lichtes », Annalen der Physik, vol. 316, no 6, , p. 270-283
- (de) Alfred Heinrich Bucherer, « Messungen an Becquerelstrahlen. Die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie », Physikalische Zeitschrift, vol. 9, no 22, , p. 755-762
- (de) Alfred Heinrich Bucherer, « Die experimentelle Bestätigung des Relativitätsprinzips », Annalen der Physik, vol. 333, no 3, , p. 513-536 (DOI 10.1002/andp.19093330305)
- (de) Emil Cohn, « Über die Gleichungen des elektromagnetischen Feldes für bewegte Körper », Annalen der Physik, vol. 312, no 1, , p. 29-56
- (de) Emil Cohn, « Zur Elektrodynamik bewegter Systeme I », Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, vol. 1904/2, no 40, , p. 1294-1303
- (de) Emil Cohn, « Zur Elektrodynamik bewegter Systeme II », Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, vol. 1904/2, no 43, , p. 1404-1416
- (en) Daniel Frost Comstock, « The Principle of Relativity », Science, vol. 31, , p. 767-772
- (en) Ebenezer Cunningham, « The Principle of Relativity in Electrodynamics and an Extension Thereof », Proceedings of the London Mathematical Society, vol. 8, , p. 77-98
- (de) Willem De Sitter, « Ein astronomischer Beweis für die Konstanz der Lichtgeschwindigkeit », Physikalische Zeitschrift, vol. 14, 1913a, p. 429
- (de) Willem De Sitter, « Über die Genauigkeit, innerhalb welcher die Unabhängigkeit der Lichtgeschwindigkeit von der Bewegung der Quelle behauptet werden kann », Physikalische Zeitschrift, vol. 14, 1913b, p. 1267
- (de) Paul Ehrenfest, « Gleichförmige Rotation starrer Körper und Relativitätstheorie », Physikalische Zeitschrift, vol. 10, , p. 918
- (de) Albert Einstein, « Zur Elektrodynamik bewegter Körper », Annalen der Physik, vol. 322, no 10, 1905a, p. 891-921 (La traduction en anglais de cet article est aussi disponible : On the Electrodynamics of Moving Bodies.)
- (de) Albert Einstein, « Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? », Annalen der Physik, vol. 323, no 13, 1905b, p. 639-643
- (de) Albert Einstein, « Das Prinzip von der Erhaltung der Schwerpunktsbewegung und die Trägheit der Energie », Annalen der Physik, vol. 325, no 8, , p. 627-633
- (de) Albert Einstein, « Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips », Annalen der Physik, vol. 328, no 6, 1907a, p. 197-198
- (de) Albert Einstein, « Über die vom Relativitätsprinzip geforderte Trägheit der Energie », Annalen der Physik, vol. 328, no 7, 1907b, p. 371-384
- (de) Albert Einstein, « Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen », Jahrbuch der Radioaktivität und Elektronik, vol. 4, 1908a, p. 411-462
- (de) Albert Einstein et Jakob Laub, « Über die elektromagnetischen Grundgleichungen für bewegte Körper », Annalen der Physik, vol. 331, no 8, 1908b, p. 532-540
- [PDF] (de) Albert Einstein, « Über die Entwicklungen unserer Anschauungen über das Wesen und die Konstitution der Strahlung », Physikalische Zeitschrift, vol. 10, no 22, , p. 817-825
- [PDF] (de) Albert Einstein, « Relativität und Gravitation. Erwiderung auf eine Bemerkung von M. Abraham », Annalen der Physik, vol. 343, no 10, , p. 1059-1064
- [PDF] (de) Albert Einstein, « Die Grundlage der allgemeinen Relativitätstheorie », Annalen der Physik, vol. 49, , p. 769-782
- (en) Albert Einstein, Relativity: The Special and General Theory, Berlin-Heidelberg-New York, Springer, , §8-9
- (en) Albert Einstein, Sidelights on relativity, Londres, Methuen & Co., (lire en ligne)
- (en) Andreas Ernst et Jong-Ping Hsu, « First Proposal of the Universal Speed of Light by Voigt in 1887 », Chinese Journal of Physics, vol. 39, no 3, , p. 211-230 (lire en ligne) Ce texte est une traduction de l'allemand à l'anglais de Voigt, 1887a.
- (en) George Francis FitzGerald, « The Ether and the Earth's Atmosphere », Science, vol. 13, , p. 390 (DOI 10.1126/science.ns-13.328.390)
- Hippolyte Fizeau, « Sur les hypothèses relatives à l’éther lumineux », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 33, , p. 349-355
- (de) Philipp Frank et Hermann Rothe, « Über die Transformation der Raum-Zeitkoordinaten von ruhenden auf bewegte Systeme », Annalen der Physik, vol. 339, no 5, , p. 825-855
- Augustin Fresnel, « Sur la diffraction de la lumière », Annales de chimie et de physique, vol. 2, , p. 239-281
- [PDF] Augustin Fresnel, « Mémoire sur la diffraction de la lumière », dans Henri de Senarmont, Émile Verdet et Léonor Fresnel, Œuvres complètes d'Augustin Fresnel, Volume 1, Paris, Imprimerie impériale, (réimpr. 1965) (1re éd. 1866) (lire en ligne), p. 248-385 Ce chapitre a été déposé à l'Académie des sciences française en juillet 1818 sous la forme d'un mémoire, voir Mémoire sur la diffraction de la lumière - M.A. Fresnel [PDF]
- (de) Friedrich Hasenöhrl, « Zur Theorie der Strahlung in bewegten Körpern », Annalen der Physik, vol. 320, no 12, , p. 344-370
- (de) Friedrich Hasenöhrl, « Zur Theorie der Strahlung in bewegten Körpern. Berichtigung », Annalen der Physik, vol. 321, no 3, , p. 589-592
- (en) Oliver Heaviside, « Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge », Electrical papers, vol. 2, , p. 490-499
- (en) Oliver Heaviside, « On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric », Philosophical Magazine, vol. 27, no 167, , p. 324-339
- (de) Heinrich Hertz, « Über die Grundgleichungen der Elektrodynamik für ruhende Körper », Annalen der Physik, vol. 276, no 8, 1890a, p. 577
- (de) Heinrich Hertz, « Über die Grundgleichungen der Elektrodynamik für bewegte Körper », Annalen der Physik, vol. 277, no 11, 1890b, p. 369-399
- (de) W. v. Ignatovski, « Einige allgemeine Bemerkungen über das Relativitätsprinzip », Physikalische Zeitschrift, vol. 11, , p. 972-976
- (de) Walter Kaufmann, « Die elektromagnetische Masse des Elektrons », Physikalische Zeitschrift, vol. 4, no 1b, , p. 54-56
- (de) Walter Kaufmann, « Über die Konstitution des Elektrons », Sitzungsberichte der Königlich Preußische Akademie der Wissenschaften, vol. 45, , p. 949-956
- (de) Walter Kaufmann, « Über die Konstitution des Elektrons », Annalen der Physik, vol. 324, no 3, , p. 487-553
- (de) Felix Klein, « Über die geometrischen Grundlagen der Lorentzgruppe », Gesammelte mathematische Abhandlungen, vol. 1, , p. 533-552
- (de) Friedrich Kottler, « Über die Raumzeitlinien der Minkowski'schen Welt », Wiener Sitzungsberichte, vol. 2a, no 121, , p. 1659-1759
- (de) Ludwig Lange, Die geschichtliche Entwicklung des Bewegungsbegriffes, vol. 1, Leipzig, Wilhelm Engelmann, (lire en ligne), p. 266-297
- (de) Ludwig Lange, Die geschichtliche Entwicklung des Bewegungsbegriffes, vol. 2, Leipzig, Wilhelm Engelmann, (lire en ligne)
- (en) Paul Langevin, « The Relations of Physics of Electrons to Other Branches of Science », International Congress of Arts and Science, vol. 7, , p. 121-156
- Paul Langevin, « Sur l’impossibilité physique de mettre en évidence le mouvement de translation de la Terre », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 140, , p. 1171-1173
- Paul Langevin, « L’Évolution de l’espace et du temps », Scientia, vol. 10, , p. 31-54
- Paul Langevin, « Remarques au sujet de la Note de Prunier », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 200, , p. 48-51
- Paul Langevin, « Sur l'expérience de M. Sagnac », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 205, , p. 304-306
- (en) Joseph Larmor, « On a Dynamical Theory of the Electric and Luminiferous Medium, Part 3, Relations with material media », Philosophical transactions of the Royal society of London, vol. 190, , p. 205-300
- (en) Joseph Larmor, Aether and Matter : chap. X, XI, Cambridge, University Press,
- (de) Jakob Laub, « Zur Optik der bewegten Körper I », Annalen der Physik, vol. 328, no 9, , p. 738-744
- (de) Max von Laue, « Die Mitführung des Lichtes durch bewegte Körper nach dem Relativitätsprinzip », Annalen der Physik, vol. 328, no 10, , p. 989-990
- (de) Max von Laue, Das Relativitätsprinzip, Brunswick, Vieweg, 1911a
- (de) Max von Laue, « Zur Diskussion über den starren Körper in der Relativitätstheorie », Physikalische Zeitschrift, vol. 12, 1911b, p. 85-87
- (de) Max von Laue, Das Relativitätsprinzip, vol. 2, Brunswick, Vieweg,
- (en) Gilbert N. Lewis, « A revision of the Fundamental Laws of Matter and Energy », Philosophical Magazine, vol. 16, , p. 705-717
- (en) Gilbert N. Lewis et Richard C. Tolman, « The Principle of Relativity, and Non-Newtonian Mechanics », Proceedings of the American Academy of Arts and Sciences, vol. 44, , p. 709-726
- (en) Gilbert N. Lewis et Edwin B. Wilson, « The Space-time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics », Proceedings of the American Academy of Arts and Sciences, vol. 48, , p. 387-507
- Hendrik Antoon Lorentz, « De l’influence du mouvement de la terre sur les phénomènes lumineux », Archives néerlandaises des sciences exactes et naturelles, vol. 21, , p. 103-176
- Hendrik Antoon Lorentz, « La Théorie electromagnétique de Maxwell et son application aux corps mouvants », Archives néerlandaises des sciences exactes et naturelles, vol. 25, 1892a, p. 363-552
- (de) Hendrik Antoon Lorentz, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern, Leyde, E. J. Brill, 1892b, p. 443-447
- (de) Hendrik Antoon Lorentz, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern, Leyde, E.J. Brill,
- (en) Hendrik Antoon Lorentz, « Simplified Theory of Electrical and Optical Phenomena in Moving Systems », Proceedings of the Royal Netherlands Academy of Arts and Sciences, vol. 1, , p. 427-442
- (en) Hendrik Antoon Lorentz, « Considerations on Gravitation », Proceedings of the Royal Netherlands Academy of Arts and Sciences, vol. 2, , p. 559-574
- (de) Hendrik Antoon Lorentz, « Über die scheinbare Masse der Ionen », Physikalische Zeitschrift, vol. 2, no 5, , p. 78-80
- (de) Hendrik Antoon Lorentz, « Weiterbildung der Maxwellschen Theorie. Elektronentheorie », Encyclopädie der mathematischen Wissenschaften, vol. 5, no 2, 1904a, p. 145-288
- (de) Hendrik Antoon Lorentz, « Elektromagnetische Erscheinungen in einem System, das sich mit beliebiger, die des Lichtes nicht erreichender Geschwindigkeit bewegt », dans Otto Blumenthal et Arnold Sommerfeld, Das Relativitätsprinzip. Eine Sammlung von Abhandlungen, 1904b, p. 6-26
- (en) H. A. Lorentz, Theory of Electrons, Leipzig,
- (de) Hendrik Antoon Lorentz, « Das Relativitätsprinzip und seine Anwendung auf einige besondere physikalische Erscheinungen », dans Otto Blumenthal et Arnold Sommerfeld, Das Relativitätsprinzip. Eine Sammlung von Abhandlungen, , p. 74-89
- (de) Hendrik Antoon Lorentz, Albert Einstein et Hermann Minkowski, Das Relativitätsprinzip, Leipzig et Berlin, B.G. Teubner, (lire en ligne)
- (de) Hendrik Antoon Lorentz, Das Relativitätsprinzip : Drei Vorlesungen gehalten in Teylers Stiftung zu Haarlem, Leipzig & Berlin, B.G. Teubner,
- Hendrik Antoon Lorentz, « La Gravitation », Scientia, vol. 16, , p. 28-59
- Hendrik Antoon Lorentz, « Deux mémoires de Henri Poincaré sur la physique mathématique », Acta Mathematica, vol. 38, , p. 247-261 (DOI 10.1007/BF02392073)
- (en) Hendrik Antoon Lorentz, The theory of electrons and its applications, Leipzig & Berlin, B.G. Teubner,
- (en) Hendrik Antoon Lorentz, « Conference on the Michelson-Morley Experiment », The Astrophysical Journal, vol. 68, , p. 345-351
- (de) Ernst Mach, Die Mechanik in ihrer Entwicklung, vol. 2, Leipzig, Brockhause, (lire en ligne [PDF])
- (en) James Clerk Maxwell, « A Dynamical Theory of the Electromagnetic Field », Philosophical Transactions of the Royal Society of London, vol. 155, , p. 459-512
- (en) James Clerk Maxwell, A Treatise on electricity and magnetism, Londres, Macmillan & Co., , p. 391
- (en) Albert Abraham Michelson, « The Relative Motion of the Earth and the Luminiferous Ether », American Journal of Science, vol. 22, , p. 120-129
- (en) Albert Abraham Michelson et Edward Williams Morley, « Influence of Motion of the Medium on the Velocity of Light », American Journal of Science, vol. 31, , p. 377-386
- (en) Albert Abraham Michelson et Edward Williams Morley, « On the Relative Motion of the Earth and the Luminiferous Ether », American Journal of Science, vol. 34, , p. 333-345
- (de) Hermann Minkowski, « Das Relativitätsprinzip », Annalen der Physik, vol. 352, no 15, , p. 927-938
- (de) Hermann Minkowski, « Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern », Nachr. Ges. Wiss. Göttingen, Mathematisch-Physikalische Klasse, , p. 53-111
- (de) Hermann Minkowski, « Raum und Zeit : 80. Versammlung Deutscher Naturforscher (Köln, 1908) », Physikalische Zeitschrift, vol. 10, , p. 75-88
- (de) Kurd von Mosengeil, « Theorie der stationären Strahlung in einem gleichförmig bewegten Hohlraum », Annalen der Physik, vol. 327, no 5, , p. 867-904
- (de) Carl Neumann, Ueber die Principien der Galilei-Newtonschen Theorie, Leipzig, B.G. Teubner,
- (de) Günther Neumann, « Die träge Masse schnell bewegter Elektronen », Annalen der Physik, vol. 350, no 20, , p. 529-579
- Isaac Newton (trad. Émilie du Châtelet), Principes mathématiques de la philosophie naturelle [« Philosophiae Naturalis Principia Mathematica »], t. 1, Paris, Dessaint & Saillant et Lambert, (1re éd. 1687), 437 p. (présentation en ligne, lire en ligne)
- (de) Gunnar Nordström, « Zur Theorie der Gravitation vom Standpunkt des Relativitätsprinzips », Annalen der Physik, vol. 347, no 13, , p. 533-554
- (de) Menyhért Palágyi, Neue Theorie des Raumes und der Zeit, Leipzig, Wilhelm Engelmann,
- (de) Max Planck, « Das Prinzip der Relativität und die Grundgleichungen der Mechanik », Verhandlungen Deutsche Physikalische Gesellschaft, vol. 8, 1906a, p. 136-141
- (de) Max Planck, « Die Kaufmannschen Messungen der Ablenkbarkeit der ?-Strahlen in ihrer Bedeutung für die Dynamik der Elektronen », Physikalische Zeitschrift, vol. 7, 1906b, p. 753-761
- (de) Max Planck, « Zur Dynamik bewegter Systeme », Sitzungsberichte der Königlich-Preussischen Akademie der Wissenschaften, vol. 1er demi-volume, no 29, , p. 542-570
- (de) Max Planck, « Bemerkungen zum Prinzip der Aktion und Reaktion in der allgemeinen Dynamik », Physikalische Zeitschrift, vol. 9, no 23, , p. 828-830
- (en) Max Planck, Eight Conferences on theoretical physics : delivered at Columbia University in the City of New York, Leipzig, S. Hirzel,
- Henri Poincaré, Théorie mathématique de la lumière, t. I, Paris, G. Carré & C. Naud,
- Henri Poincaré, « A propos de la Théorie de M. Larmor », L'Éclairage électrique (1re page), vol. 5, , p. 5-14
- Henri Poincaré, « La mesure du temps », Revue de métaphysique et de morale, vol. 6, , p. 1-13
- Henri Poincaré, « Les relations entre la physique expérimentale et la physique mathématique », Revue générale des sciences pures et appliquées, vol. 11, 1900a, p. 1163-1175
- Henri Poincaré, « La théorie de Lorentz et le principe de réaction », Archives néerlandaises des sciences exactes et naturelles, vol. 5, 1900b, p. 252-278
- Henri Poincaré, « Sur les principes de la mécanique », dans Bibliothèque du Congrès international de philosophie, , p. 457-494
- Henri Poincaré, Électricité et optique, Paris, Gauthier-Villars,
- Henri Poincaré, La Science et l’Hypothèse, Paris, E. Flammarion,
- Henri Poincaré, « L’Histoire de la Physique mathématique : Chap. VII-IX », La Valeur de la Science, Paris, Flammarion, , p. 129-159
- Henri Poincaré, La Valeur de la Science, Paris, E. Flammarion, 1905a
- Henri Poincaré, « Sur la dynamique de l’électron », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 140, 1905b, p. 1504-1508
- Henri Poincaré, « Sur la dynamique de l’électron », Rendiconti del Circolo matematico di Palermo, Circolo Matematico di Palermo, vol. 21, , p. 129-176
- Henri Poincaré, « Science et Méthode : Livre III, La mécanique nouvelle », Science et Méthode, Paris, Flammarion, , p. 215-272
- Henri Poincaré, « La Mécanique nouvelle (Lille) », Revue scientifique, , p. 38-48
- (de) Henri Poincaré, « Die neue Mechanik », Himmel und Erde, Leipzig, B. G. Teubner, vol. 23,
- Henri Poincaré, Dernières pensées, Paris, E. Flammarion,
- Walter Ritz, « Recherches critiques sur l'Électrodynamique Générale », Annales de Chimie et de Physique, vol. 13, , p. 145-275
- (en) Alfred A. Robb, Optical Geometry of Motion: A New View of the Theory of Relativity, Cambridge, W. Heffer,
- Georges Sagnac, « L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme », Comptes Rendus, Paris, Gauthier-Villars, vol. 157, , p. 708-710
- Georges Sagnac, « Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant », Comptes Rendus, Paris, Gauthier-Villars, vol. 157, , p. 1410-1413
- (en) George Frederick Charles Searle, « On the Steady Motion of an Electrified Ellipsoid », Philosophical Magazine, vol. 44, no 269, , p. 329-341
- (de) Arnold Sommerfeld, « Zur Relativitätstheorie I: Vierdimensionale Vektoralgebra », Annalen der Physik, vol. 337, no 9, 1910a, p. 749-776
- (de) Arnold Sommerfeld, « Zur Relativitätstheorie II: Vierdimensionale Vektoranalyis », Annalen der Physik, vol. 338, no 14, 1910b, p. 649-689
- (en) George Gabriel Stokes, « On the Aberration of Light », Philosophical Magazine, vol. 27, , p. 9-15
- (de) Heinrich Streintz, Die physikalischen Grundlagen der Mechanik, Leipzig, B.G. Teubner,
- (en) Joseph John Thomson, « On the Electric and Magnetic Effects produced by the Motion of Electrified Bodies », Philosophical Magazine, vol. 11, no 68, , p. 229-249
- (en) Richard Chase Tolman, « The mass of a moving body », Philosophical Magazine, vol. 23, , p. 375-380
- (de) Vladimir Varićak, « Zum Ehrenfestschen Paradoxon », Physikalische Zeitschrift, vol. 12, , p. 169
- (de) Vladimir Varićak, « Über die nichteuklidische Interpretation der Relativitätstheorie », Jahresbericht der Deutschen Mathematiker-Vereinigung, vol. 21, , p. 103-127
- (de) Woldemar Voigt, « Ueber das Doppler’sche Princip », Nachr. Königl. Ges. Wiss. u. Georg-Augusts-Univ. Göttingen, Dieterichsche Verlags-Buchhandlung, no 2, , p. 41-51
- (de) Wilhelm Wien, « Über die Möglichkeit einer elektromagnetischen Begründung der Mechanik », Annalen, Joh. Ambr. Barth, vol. 310, no 7, , p. 501-513 (DOI 10.1002/andp.19013100703)
- (de) Wilhelm Wien, « Über die Differentialgleichungen der Elektrodynamik für bewegte Körper: Teil I, Teil II », Annalen der Physik, vol. 318, no 4, 1904a, p. 641-662
- (de) Wilhelm Wien, « Erwiderung auf die Kritik des Hrn. M. Abraham », Annalen der Physik, Johann Ambrosius Barth, vol. 319, no 8, 1904b, p. 635-637
Sources secondaires
[modifier | modifier le code]- (en) Christopher Jon Bjerknes, « A Short History of the Concept of Relative Simultaneity in the Special Theory of Relativity », Episteme, vol. 6,
- (en) Max Born, Physics in my Generation, Londres et New York, Pergamon Press,
- (de) Max Born, Die Relativitätstheorie Einsteins, Berlin-Heidelberg-New York, Springer, , 501 p. (ISBN 3-540-00470-X), p. 172-194
- [PDF] (en) Harvey R. Brown, « The origins of length contraction: I. The FitzGerald-Lorentz deformation hypothesis », American Journal of Physics, vol. 69, no 10, , p. 1044–1054
- Claude Boucher, Une brève histoire des idées de Galilée à Einstein, Fides, , 291 p. (ISBN 978-2-7621-2863-5, lire en ligne)
- (en) Olivier Darrigol, « The Mystery of the Einstein-Poincaré Connection », Isis, vol. 95, no 4, , p. 614–626 (résumé)
- [PDF] (en) Olivier Darrigol, « The Genesis of the theory of relativity », Séminaire Poincaré, vol. 1, , p. 1–22
- (en) Olivier Darrigol, Electrodynamics from Ampère to Einstein, Oxford, Clarendon Press, , 532 p. (ISBN 0-19-850594-9)
- (en) Robert DiSalle, « Space and Time: Inertial Frames », dans Edward N. Zalta, The Stanford Encyclopedia of Philosophy,
- (en) Albert Einstein, « The Swiss Years: Writings, 1900-1909 », dans John Stachel, David C. Cassidy et Robert Schulmann, The Collected Papers of Albert Einstein, 2. Princeton, Princeton University Press, (ISBN 0-691-08526-9)
- (de) Albrecht Fölsing, Albert Einstein. Eine Biographie, Francfort-sur-le-Main, Suhrkamp, , 959 p. (ISBN 3-518-38990-4)
- (de) Peter Galison, Einsteins Uhren, Poincarés Karten. Die Arbeit an der Ordnung der Zeit, Francfort, Fischer, , 382 p. (ISBN 3-10-024430-3)
- Traduit en français : Peter Galison (trad. de l'anglais américain par Bella Arman), L'Empire du temps : Les horloges d'Einstein et les cartes de Poincaré [« Einstein's clocks, Poincaré's maps »], Paris, Gallimard, coll. « Folio / essais » (no 476), , 477 p. (ISBN 978-2-07-031924-4, OCLC 165078421)
- (en) Boyce Gibson et William Ralph, « The Philosophy of Melchior Palagyi. (I) Space-Time and the Criticism of Relativity », Journal of Philosophical Studies, vol. 3, no 9, , p. 15–28
- (de) Domenico Giulini, « Das Problem der Trägheit », Preprint, Max-Planck Institut für Wissenschaftsgeschichte, vol. 190, , p. 11–12, 25–26
- (en) Domenico Giulini, « Über die Herkunft der Speziellen Relativitätstheorie », dans Herbert Hunziker, Der jugendliche Einstein und Aarau, Bâle, Birkhäuser, (ISBN 3764374446)
- (en) Hubert Goenner, « On the history of geometrization of space-time », Heraeus-Seminar, vol. 414,
- (de) Klaus Hentschel, Interpretationen und Fehlinterpretationen der speziellen und der allgemeinen Relativitätstheorie durch Zeitgenossen Albert Einsteins, Bâle - Boston - Bonn, Birkhäuser, , 574 p. (ISBN 3-7643-2438-4)
- (en) Gerald Holton, Thematic Origins of Scientific Thought : Kepler to Einstein, Cambridge, Harvard University Press, , 522 p. (ISBN 0-674-87747-0)
- Gerald Holton, « Aux origines de la relativité restreinte », dans L'Imagination Scientifique, Paris, Gallimard, Holten est décrit comme un spécialiste de la relativité restreinte dans Einstein ou Poincaré ?, Pour la Science, avril 2005
- (en) Michel Janssen, A Comparison between Lorentz's Ether Theory and Special Relativity in the Light of the Experiments of Trouton and Noble, Thèse de doctorat disponible en plusieurs fichiers PDF à http://www.tc.umn.edu/~janss011/
- [PDF] (en) Michel Janssen et John Stachel, The Optics and Electrodynamics of Moving Bodies, (lire en ligne)
- (en) Michel Janssen et Matthew Mecklenburg, « From classical to relativistic mechanics: Electromagnetic models of the electron. », dans V. F. Hendricks, et.al., Interactions: Mathematics, Physics and Philosophy, Dordrecht, Springer, , p. 65–134
- (en) Shaul Katzir, « Poincaré’s Relativistic Physics: Its Origins and Nature », Physics in perspective, vol. 7, , p. 268–292 (DOI 10.1007/s00016-004-0234-y)
- (en) G.H. Keswani et C.W. Kilmister, « Intimations Of Relativity: Relativity Before Einstein », The British Journal for the Philosophy of Science, vol. 34, , p. 343–354
- (de) Max von Laue, Die Relativitätstheorie, Brunswick, Friedr. Vieweg & Sohn, , 4e éd.
- (en) A. A. Logunov, Henri Poincaré and relativity theory, Moscou, Nauka, (ISBN 5-02-033964-4, lire en ligne)
- (en) M. N. Macrossan, « A Note on Relativity Before Einstein », The British Journal for the Philosophy of Science, vol. 37, , p. 232–234
- (en) Arthur I. Miller, Albert Einstein’s special theory of relativity : Emergence (1905) and early interpretation (1905–1911), Reading, Addison–Wesley, , 466 p. (ISBN 0-201-04679-2)
- Salah Ould Moulaye Ahmed, De Thalès à Einstein, l'histoire de la science à travers ses grands hommes, Levallois-Perret, Studyrama, coll. « Principes », , 159 p. (ISBN 978-2-7590-0251-1)
- [PDF] (en) John D. Norton, « Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905 », Archive for History of Exact Sciences, vol. 59, , p. 45–105
- (en) John D. Norton, « Einstein, Nordström and the early demise of scalar, lorentz covariant theories of gravitation », dans Jürgen Renn, The Genesis of General Relativity (Vol. 1), Kluwer,
- (de) Abraham Pais, „Raffiniert ist der Herrgott …“ : Albert Einstein, eine wissenschaftliche Biographie, Heidelberg, Spektrum, (ISBN 3-8274-0529-7)
- (de) Wolfgang Pauli, « Die Relativitätstheorie », Encyclopädie der mathematischen Wissenschaften, vol. 5, no 2, (lire en ligne)
- (en) Jürgen Renn, « Introduction », dans Jürgen Renn, Einstein's Annalen Papers. The Complete Collection 1901-1922, Berlin, Wiley-VCH, (ISBN 352740564X)
- (en) Wolfgang Rindler, Relativity : Special, General, and Cosmological, Oxford, Oxford University Press, , 428 p. (ISBN 0-19-850836-0)
- (en) Kenneth Schaffner, Nineteenth-century aether theories, Oxford, Pergamon Press, , 296 p. (ISBN 0-08-015674-6), p. 99–117, 255–273
- Raymond A. Serway (trad. Robert Morin et Céline Temblay), Physique III. Optique et physique moderne [« Physics for Scientists and Engineers / With Modern Physics »], Laval (Québec), Éditions Études Vivantes, , 3e éd., 776 p. (ISBN 2-7607-0542-0, présentation en ligne, lire en ligne)
- (en) John Stachel, « Einstein and Michelson: the Context of Discovery and Context of Justification », Astronomische Nachrichten, vol. 303, , p. 47–53
- (en) John Stachel, Einstein from "B" to "Z", Boston, Birkhäuser, , 556 p. (ISBN 0-8176-4143-2, lire en ligne)
- (en) Richard Staley, Einstein's generation. The origins of the relativity revolution, Chicago, University of Chicago Press, , 494 p. (ISBN 978-0-226-77057-4 et 0-226-77057-5, lire en ligne)
- Marie-Antoinette Tonnelat, Histoire du principe de relativité, Paris, Flammarion, coll. « Nouvelle bibliothèque scientifique », (EAN 9782403044614).
- (en) Scott A. Walter, « Minkowski, mathematicians, and the mathematical theory of relativity », dans H. Goenner, J. Renn, J. Ritter et T. Sauer, Einstein Studies, Birkhäuser, 1999a, p. 45–86
- (en) Scott A. Walter, « The non-Euclidean style of Minkowskian relativity », dans J. Gray, The Symbolic Universe: Geometry and Physics, Oxford University Press, 1999b, p. 91–127
- (en) Scott A. Walter, « Henri Poincaré and the theory of relativity », dans Jürgen Renn, Albert Einstein, Chief Engineer of the Universe: 100 Authors for Einstein, Berlin, Wiley-VCH, , p. 162–165
- (en) Scott A. Walter, « Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910 », dans Jürgen Renn et M. Schemmel, The Genesis of General Relativity, Berlin, Springer, , p. 193–252
- (en) Andrew Warwick, Masters of theory : Cambridge and the rise of mathematical physics, Chicago, University of Chicago Press, , 572 p. (ISBN 0-226-87375-7, lire en ligne)
- (en) Edmund Taylor Whittaker, A History of the Theories of Aether and Electricity, Dublin, Longman, Green and Co, , 1re éd.
- (en) Edmund Taylor Whittaker, A History of the Theories of Aether and Electricity, vol. 1 : The classical theories, Londres, Nelson, , 2e éd.
- (en) Edmund Taylor Whittaker, A History of the Theories of Aether and Electricity, vol. 2 : The modern theories 1900-1926, Londres, Nelson, , 2e éd.
- (en) Elie Zahar, Einstein's Revolution : A Study in Heuristic, Chicago, Open Court Publishing Company, , 373 p. (ISBN 0-8126-9067-2)





















![{\displaystyle [\Delta \Psi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\Psi }{\partial t^{2}}}=0\ ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cfcc8c2f0362758049eb6504e215cfa94e858eb)