Cinématique

En physique, la cinématique (du grec kinêma, le mouvement) est l'étude des mouvements indépendamment des causes qui les produisent, ou, plus exactement, l'étude de tous les mouvements possibles. À côté de la notion d'espace qui est l'objet de la géométrie, la cinématique introduit la notion de temps. À ne pas confondre avec la cinétique ![]() , un terme plus général qui concerne la vitesse et les mécanismes d'une grande variété de processus ; en mécanique, cinétique est utilisé comme adjectif pour qualifier deux grandeurs impliquant aussi la masse : le moment cinétique et l'énergie cinétique.
, un terme plus général qui concerne la vitesse et les mécanismes d'une grande variété de processus ; en mécanique, cinétique est utilisé comme adjectif pour qualifier deux grandeurs impliquant aussi la masse : le moment cinétique et l'énergie cinétique.
On peut dater la naissance de la cinématique moderne à l'allocution de Pierre Varignon le devant l'Académie royale des sciences de Paris[1]. À cette occasion il définit la notion d'accélération et montre comment il est possible de la déduire de la vitesse instantanée à l'aide d'une simple procédure de calcul différentiel.
Toute figure mobile peut être regardée comme un système de points mobiles, il est alors naturel de commencer par l'étude du mouvement du point mobile isolé.
Définitions de base[modifier | modifier le code]
Cinématique du point[modifier | modifier le code]
Il faut d'abord définir un référentiel, c'est-à-dire un repère de l’espace et une référence pour le temps, une horloge[2] ; on utilise en général le référentiel lié au laboratoire, par exemple dont les axes suivent les arêtes des murs de la pièce, ou bien celle de la table, ou encore les directions géographiques Nord-Sud, Est-Ouest et haut-bas (si le laboratoire est immobile par rapport au sol). L'objet de base est le point, sans dimension. Dans un repère cartésien, un point M est défini par ses coordonnées (x, y, z, t) et noté M(x, y, z, t).
Un objet réel est un volume, constitué d'une infinité de points. La cinématique du point consiste donc à étudier un point particulier d'un solide. On choisit des points caractéristiques, dont l'étude est simple et/ou donne des renseignements pertinents ; ce sont typiquement le centre de gravité du solide, qui joue un rôle important en dynamique, ou bien le point de contact du solide avec un autre. Si le solide est de petite dimension par rapport à son déplacement, et que l'on ne s'intéresse pas à sa rotation propre dans le référentiel, alors on peut se contenter de cette étude du point ; c'est le cas par exemple de la révolution des planètes dans le système solaire.
Les coordonnées définissent le vecteur position, qui dépend ainsi de la position et du temps[3].
Le vecteur obtenu en dérivant les coordonnées par rapport au temps définit le vecteur vitesse. Le vecteur vitesse est indépendant du choix du point origine[3].
Le vecteur obtenu en dérivant les composantes du vecteur vitesse par rapport au temps définit le vecteur accélération
Le vecteur obtenu en dérivant les composantes du vecteur accélération par rapport au temps définit le vecteur d'à-coup
La mécanique du point permet de prévoir la position en fonction du temps, à partir de la vitesse initiale et des forces.
L'équation horaire du mouvement
correspond à l’équation paramétrique d'une courbe ; on peut souvent réduire ceci à un système de trois équations cartésiennes
qui, dans le cas le plus simple, sont du type linéaire :
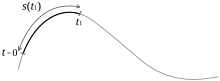
Cette courbe est l’ensemble des points par où passe le centre d'inertie du mobile. On définit alors l'abscisse curviligne, notée s, la distance parcourue sur la courbe par rapport à un point de référence (la position du centre d'inertie du mobile à t = 0). Pour un petit déplacement de M(x,y,z,t) à M(x+dx, y+dy, z+dz, t+dt), l'abscisse curviligne est assimilable à un segment, d'où :
On a donc :
- .
La notion commune de vitesse est en fait la dérivée de l'abscisse curviligne. On parle souvent de « vitesse scalaire »[4] :
- .
On a en fait
- .
Cinématique du solide[modifier | modifier le code]
Il est souvent important de prendre en compte la rotation du solide. Le premier modèle est celui du solide indéformable : si l'on considère deux points M1 et M2 quelconque du solide, alors la distance M1M2 reste constante au cours du temps.
On peut étudier la trajectoire de chaque point du solide, mais on peut aussi définir le mouvement du solide de manière globale. Pour cela, on attache un repère au solide, (O1, x1, y1, z1) ; l'origine O1 est un point présentant un intérêt particulier, comme le centre de gravité, le centre d'un pivot (centre du cylindre d'un perçage), un sommet. La position du solide est alors définie par six paramètres :
- les coordonnées de O1 dans le repère du référentiel ;
- les angles d'Euler, pour l'orientation dans l'espace.
Cinématique des fluides[modifier | modifier le code]
Un fluide — liquide ou gaz — est constitué de nombreuses particules microscopiques, des molécules. Ces particules ont un mouvement chaotique, dit « mouvement brownien ». À ce mouvement se superpose un mouvement d'ensemble, le courant. Il serait illusoire de vouloir étudier chaque particule, on utilise donc une description statistique du mouvement.
Description qualitative des mouvements[modifier | modifier le code]
Le mouvement d'un solide est en général caractérisé par deux termes : son type et sa nature. Le type de mouvement indique la manière dont la position évolue. Les termes typiquement employés sont :
- mouvement quelconque ;
- mouvement plan : les trajectoires des points sont planes, les plans sont tous parallèles (voir ci-dessous),
- mouvement de translation : les trajectoires de tous les points du solide sont des segments courbes identiques, parallèles entre eux, le solide garde la même orientation au cours du mouvement,
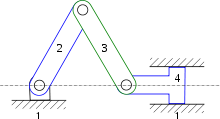
- mouvement de translation circulaire (schéma b ci-contre) : c'est le cas du balai d'essuie-glace d'autocar, et de manière générale le mouvement obtenu avec un parallélogramme déformable ; les trajectoires sont des arcs de cercle qui ont même rayon, même longueur (ouverture angulaire), mais projetés sur un plan, ils ont des centres différents,
- mouvement de translation rectiligne de direction (Δ) : la trajectoire de tous les points du solide sont des segments de droite parallèles ) à la droite (Δ),
- mouvement de rotation d'axe (Δ) : les trajectoires de tous les points du solide sont des arcs de cercle dont le plan est perpendiculaire à la droite (Δ), et dont le centre est sur la droite (Δ) ; projetés sur un plan, les arcs de cercle sont concentriques.
- mouvement de translation : les trajectoires de tous les points du solide sont des segments courbes identiques, parallèles entre eux, le solide garde la même orientation au cours du mouvement,
La nature du mouvement donne une indication sur l'évolution de la vitesse :
- mouvement uniforme : la norme des vecteurs vitesse est constante ; cela ne peut être valable que pour une durée définie, puisqu'un mouvement a toujours une phase de démarrage et d'arrêt ;
- mouvement varié : la norme des vecteurs vitesse varie,
- mouvement uniformément varié : la norme des vecteurs vitesse varie de manière linéaire avec le temps ; cela ne peut être valable que pour une durée définie, puisque la norme finit par croître de manière infinie ; cette situation est une approximation des phases de démarrage et d'arrêt des machines.
On a ainsi quatre mouvements solides simples.
| Type | Nature | |
|---|---|---|
| Translation rectiligne |
Rotation | |
| Uniforme | Translation rectiligne uniforme |
Rotation uniforme |
| Uniformément varié |
Translation rectiligne uniformément variée |
Rotation uniformément variée |
En cinématique du point, on ne parle pas de mouvement de rotation, mais de mouvement circulaire.
Si l'on considère maintenant la trajectoire d'un point donné, on la caractérise par un « élément géométrique caractéristique », c'est-à-dire la courbe mathématique qu'il suit, si tant est qu'on puisse la définir de manière simple. Typiquement, c'est un « arc de cercle de entre A », un « segment de droite de direction », ou une courbe plus complexe (ellipse, parabole, hyperbole).
Mouvement plan et repère de Frenet[modifier | modifier le code]

Considérons un plan P, muni d'un repère (O, x, y). On s'intéresse à la distance de chaque point du solide par rapport à ce plan. Si, au cours du mouvement, cette distance reste constante pour chacun des points du solide, alors on dit que le solide a un mouvement plan[5]. Ce plan peut être horizontal, vertical ou bien incliné. Ainsi, toutes les trajectoires sont plane, dans un plan parallèle à P. Tous les vecteurs vitesse et accélération sont parallèles à P. Tous les axes de rotation sont perpendiculaires à P.
On peut ainsi ne travailler qu'avec deux coordonnées spatiales, x et y ; on projette les positions et trajectoires sur le plan P.
Les exemples typiques de mouvement plan sont :
- les mouvements à accélération centrale, dont les mouvements des planètes et des comètes autour du Soleil ;
- les mouvements balistiques et de chute libre sans vent de travers ;
- les mouvements de rotation autour d'un axe immobile (Δ) ; le plan P est perpendiculaire à l'axe (Δ) (qui est donc l'axe z ) ;
- les mouvements des solides restant en contact avec un plan, horizontal ou incliné, par exemple une voiture sur une route plane ;
- les mouvements des mécanismes dont les axes des pivots sont tous parallèles à une même droite (Δ), et dont les axes des glissières sont perpendiculaires à (Δ) ; le plan P est perpendiculaire à l'axe (Δ) (qui est donc l'axe z ).
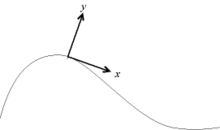
Pour simplifier les calculs, on définit souvent un repère local dit « de Frenet » pour chaque instant ; en un point de la courbe, l'axe des x est la tangente à la courbe et orienté dans le sens du mouvement, et l'axe des y est la normale à la courbe orienté de sorte que le repère soit direct[6]. Ce n'est pas un référentiel mobile par rapport au référentiel de l'étude, c'est un repère instantané, défini juste à un instant t pour simplifier l'écriture des grandeurs à cet instant donné. Le référentiel reste celui du laboratoire, seule change la manière dont on exprime les composantes des vecteurs.
Mouvement simple en cinématique du point[modifier | modifier le code]
Le problème est donc ramené à trouver la fonction donnant la position sur la courbe en fonction du temps, soit s(t). On appelle diagramme horaire le graphe de [t,s(t)] : de tels diagrammes sont très utilisés pour les trains (par exemple en France, le CHAIX donne pour l'ensemble du réseau les diagrammes horaires, ce qui permet de calculer les tableaux de correspondance de transport de gare en gare).
Mouvement rectiligne[modifier | modifier le code]
Le cas le plus simple est celui du mouvement rectiligne : la trajectoire décrite est une droite. Mouvement dans lequel tout segment reliant deux points du solide reste parallèle à lui-même au cours du temps est aussi une définition classique du mouvement rectiligne.
|
Mouvement rectiligne uniforme (MRU)[modifier | modifier le code]
Le mouvement est dit rectiligne uniforme si la vitesse est constante ; cela correspond au mouvement d'un objet lancé dans l'espace hors de toute interaction, ou encore au mouvement d'un objet glissant sans frottement. On a :
L'abscisse curviligne s est alors une fonction linéaire du temps.
En étude des vitesses, ce type de mouvement a une propriété fondamentale : tous les points d'un solide en translation rectiligne uniforme ont le même vecteur vitesse. On considère de plus qu'un solide immobile est en translation rectiligne uniforme : L'immobilité est un cas particulier du mouvement rectiligne uniforme.
Mouvement rectiligne uniformément accéléré (MRUA)[modifier | modifier le code]
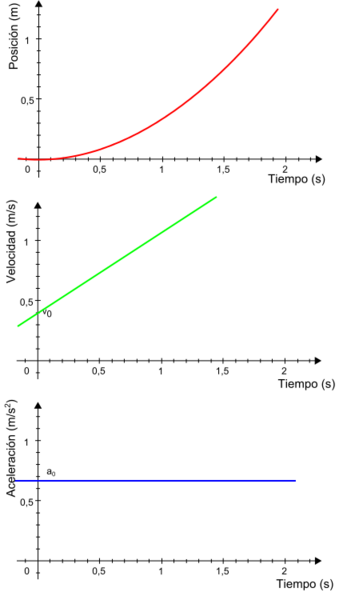
Le mouvement peut être rectiligne uniformément accéléré — MRUA — (on dit aussi rectiligne uniformément varié) ; le vecteur accélération est constant. Ceci correspond à la chute libre (sans frottement) d'un objet lâché avec une vitesse initiale nulle ou dirigée verticalement ; ou bien un mouvement sans frottement sur un plan incliné d'un mobile lâché avec une vitesse initiale nulle ou dirigée par la pente du plan incliné. On a l'accélération
qui est constante, soit :
où est la vitesse à t = 0 (elle est nulle si l'objet est lâché sans vitesse initiale), et
(on prend x(t = 0) = x0). La vitesse est une fonction linéaire du temps, et l'abscisse curviligne est une fonction parabolique du temps.
Dans le cas de la chute d'un corps, a = –g, où g est l'accélération de la pesanteur au lieu considéré.
Le temps nécessaire au solide pour atteindre une position, se calcule en fonction de l'accélération et en fonction des conditions initiales.
Exemple[modifier | modifier le code]
Prenons une fusée dont la position x varie à chaque instant t ; elle suit une trajectoire rectiligne A–B. Elle subit une accélération a de 6 m/s2, et on prend x(t= 0) = 0 et v(t = 0) = 0 :
Donc, après 5 secondes de vol depuis A, la fusée est à 62 × 52 = 75 mètres de A.
Maintenant pour connaître sa vitesse, on calcule :
Donc si la fusée est en vol depuis 5 secondes, sa vitesse est de 30 m/s.
Mouvement circulaire[modifier | modifier le code]
Le centre d'inertie du mobile décrit un cercle. Cela peut être un mobile contraint à suivre cette trajectoire comme une bille dans une gouttière circulaire, un pendule à fil dont le fil reste tendu, ou un train sur un rail circulaire.
Le vecteur vitesse varie, donc le mobile subit une accélération. Ceci justifie la distinction entre la notion de mouvement varié (dont la norme de la vitesse varie) et de mouvement accéléré (dont le vecteur vitesse varie, en norme et/ou en direction).
Mouvement circulaire uniforme[modifier | modifier le code]
Le mouvement est dit circulaire uniforme si la norme de la vitesse est constante. L'équation horaire est alors du type :
où , sont les coordonnées du centre du cercle, le rayon du cercle et la vitesse angulaire du centre d'inertie du mobile, exprimée en radians par seconde (rad/s ou rad s−1). La plupart du temps, on choisit , l'équation horaire devient alors :
On a :
Le vecteur vitesse est tangent au cercle ; on a :
On voit aussi que l'accélération est toujours dirigée vers le centre du cercle (on parle d’accélération centrale centripète), et sa norme vaut
Ceci explique que lorsque l'on tourne en voiture, plus le virage est serré ( est faible), plus l'accélération est importante.

Dans le repère de Frenet, on a :
- et
Mouvement circulaire uniformément varié[modifier | modifier le code]
Le mouvement est dit circulaire uniformément varié si la vitesse angulaire varie selon une loi affine :
Ce modèle permet de décrire le mouvement d'un point d'une machine tournante au démarrage ou à l'arrêt.
La grandeur constante α est l'accélération angulaire, elle s'exprime en radians par seconde au carré (rad/s2 ou rad s−2). L'angle de rotation suit une loi quadratique :
L'abscisse curviligne vérifie , soit et donc une accélération tangentielle Les équations horaires sont :
avec et Le mobile subit toujours une accélération normale centripète
Dans le repère de Frenet, on a :
- et
Attention ! Le mouvement du pendule à fil ou d'une bille dans une gouttière est circulaire mais ni uniforme, ni uniformément varié.
Mouvement elliptique[modifier | modifier le code]
Le centre d'inertie du mobile décrit une ellipse (le mouvement circulaire est un cas particulier de mouvement elliptique). Cela peut être le mouvement d'une voiture sur une courbe suivant un arc d'ellipse, ou bien celui d'un satellite autour d'une planète dans un référentiel galiléen dans lequel la planète est fixe, ou encore le mouvement d'une planète ou d'une comète autour d'une étoile ; le centre de gravité du système est alors à un des foyers de l'ellipse (ce centre de gravité se confond quasiment avec le plus massif des deux objets quand le rapport des deux masses est très élevé).
On définit la vitesse aréolaire comme étant l'aire balayée par un rayon joignant le foyer au centre d'inertie du mobile.
Dans le cas des mouvements orbitaux, le moment cinétique par rapport à un foyer F est constant (ceci peut se déduire du principe de conservation du moment cinétique d'un système isolé) :
où
- est le vecteur reliant le foyer au mobile ;
- est la quantité de mouvement du mobile (m est la masse, le vecteur vitesse)
- désigne le produit vectoriel.
Mouvement quelconque en cinématique du point[modifier | modifier le code]
Pour considérer les mouvements quelconques, on peut travailler de deux manières :
- considérer localement la tangente au mouvement, et utiliser les notions développées avec les trajectoires rectilignes uniformes
- considérer localement que l'on a un mouvement circulaire uniforme.
Ces deux approximations sont valables si l'on considère des temps courts.
Approximation tangentielle[modifier | modifier le code]
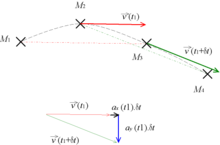
En général, le mouvement du centre d'inertie d'un mobile est enregistré de manière échantillonnée, c'est-à-dire que l'on a des points discrets correspondant à des positions à des instants séparés d'une durée Si l'on considère trois points consécutifs et correspondant à des instants et .
La première approximation consiste à dire que la tangente en est parallèle à la corde Ceci est légitimé par un théorème mathématique disant que pour une fonction continue et dérivable sur un intervalle, il existe un point de cet intervalle dont la dérivée vaut la pente entre les points extrêmes de la courbe sur cet intervalle (voir Théorème des accroissements finis). On peut aussi rapprocher cela du fait que sur un cercle, la médiatrice d'une corde passe par le milieu de la corde et est perpendiculaire à la tangente au milieu de la corde (puisque c'est un rayon).
La deuxième approximation consiste à estimer la norme de la vitesse constante entre et ce qui est acceptable si la durée est petite par rapport à l'accélération tangentielle. On estime donc que l'on a :
La variation de ce vecteur vitesse donne le vecteur accélération. La composante tangentielle vaut :
ou, par approximation :
en effet, dans le repère de Frenet, on a et on fait l'approximation (approximation d'ordre 0). La composante normale est donnée par la variation de direction du vecteur vitesse ; on a par définition du repère de Frenet, soit :
- (approximation d'ordre 1, puisque l'ordre 0 est nul).
Dans le cas où le mouvement est lent par rapport à la précision de la mesure, la position enregistrée va avoir des variations dues aux incertitudes de mesure ; ainsi, au lieu d'avoir une courbe lisse, on va avoir une courbe présentant des oscillations (du bruit). Si l'on prend les points tels quels, on va calculer des vitesses instantanées incohérentes qui vont se répercuter sur les calculs des accélérations. Si les données sont traitées de manière informatique, on effectue donc un lissage des données.
Rayon de courbure[modifier | modifier le code]
Choisissons sur une courbe C un point M0 comme origine, puis désignons par M(t) la position du mobile à l'instant t, et par s = M0M l'abscisse curviligne du point M. La vitesse du mobile peut s'écrire :
où désigne le vecteur unitaire tangent à C.
On définit en tout point le rayon de courbure ρ de la trajectoire par :
où dθ est l'angle formé entre les deux vecteurs vitesse aux points M(t) et M(t + dt).
Exemple[modifier | modifier le code]
Dans le repère , considérons le mouvement d'équation horaire :
Le vecteur position s'écrit :
Le vecteur vitesse s'écrit :
Le module du vecteur vitesse est :
- , c'est une constante.
L'accélération tangentielle est :
Le vecteur accélération totale est :
Son module est :
- , c'est une constante.
Les accélérations totale, tangentielle et normale forment un triangle rectangle ayant l'accélération totale pour hypoténuse ; alors d'après le théorème de Pythagore on a , ce qui donne ici :
Or on a :
- ,
donc :
- , c'est une constante.
Cette courbe n'est autre qu'un cercle.
Enregistrement du mouvement[modifier | modifier le code]
L'enregistrement du mouvement, c'est-à-dire le relevé de la position et de la vitesse, est le fondement de l'étude cinématique.
Enseignement et travaux pratiques[modifier | modifier le code]
Le prérequis pour faire une étude cinématique consiste à enregistrer le mouvement. Dans le cadre de l'enseignement, on étudie en général le mouvement de palets autoporteurs. Ce sont des appareils cylindriques sur coussin d'air (un jet d'air les maintient quelques millimètres au-dessus de la table), ce qui leur permet de glisser sans frottement (on néglige les frottements de l'air). On utilise une table conductrice d'électricité avec un papier spécial ; reliés à une base de temps (une horloge qui délivre des impulsions électriques à des instants espacés de ), les palets autoporteurs provoquent des étincelles qui marquent le papier spécial. Ainsi, chaque point sur le papier correspond à la position du centre d'inertie à un instant donné. Ceci permet d'étudier le mouvement sur un plan horizontal et incliné, éventuellement avec deux palets (indépendants, reliés par un élastique ou s'entrechoquant).
Pour étudier la chute libre, on utilise un objet lourd et profilé, une sorte d'obus métallique, que l'on fait tomber verticalement dans une cage (afin qu'il ne bascule pas après l'impact sur la zone de réception). On colle une feuille de papier dessus, et la cage est munie d'une « lance rotative », projetant un fin jet d'encre. La lance tournant selon une fréquence constante, chaque trait sur le papier marque le point présent au niveau de la lance à un moment donné.
Grâce à la réduction du coût du matériel informatique, on peut maintenant disposer d'un caméscope numérique. On peut donc filmer le mouvement (le caméscope étant fixe, posé sur un pied), puis en affichant les images une par une, relever la position de l'objet pour chaque image (en France, la vidéo enregistre 25 images par seconde).
Sur la route[modifier | modifier le code]
Les forces de police s'intéressent en général uniquement à la vitesse et disposent de cinémomètres à effet Doppler-Fizeau, improprement appelés « radars ». Ceux-ci permettent de mesurer directement la vitesse instantanée. Lorsque s'est produit un accident, les traces de freinage, et les éventuelles traces d'impact sur le mobilier urbain ou les rails de sécurité, permettent de recomposer la trajectoire des véhicules. Notamment, la longueur des traces de freinage permet d'estimer la vitesse avant le début du freinage (la force de freinage étant constante).
Le conducteur, quant à lui, dispose d'un tachymètre (indicateur de vitesse) sur son tableau de bord, qui lui permet de connaître également sa vitesse instantanée. Il se base en général sur la fréquence de rotation des roues ; par exemple, une pastille réfléchissante est collée sur l'arbre de transmission, et une cellule photo-détectrice permet de connaître le temps qui s'écoule entre deux passage de la pastille, donc la fréquence de rotation et par là la vitesse.
Les cyclistes mettent un aimant sur un rayon de la roue avant et un détecteur magnétique sur la fourche, ce qui leur permet, de la même manière, de mesurer la vitesse et le chemin parcouru. D'anciens systèmes étaient basés sur une petite roue tournant, entraînée par la roue du vélo.
Les marcheurs disposent de podomètres qui détectent les vibrations caractéristiques du pas. Le marcheur ayant rentré la longueur moyenne de son pas, l'appareil peut déterminer la distance parcourue ainsi que la vitesse (produit de la longueur du pas par la fréquence de pas).
La vidéo couplée à l'analyse informatisée des images permet également de déterminer la position et la vitesse des véhicules. Ceci est utilisé pour estimer le trafic et détecter les embouteillages, et pourrait faire son apparition dans les véhicules dans un avenir proche, afin de fournir une aide à la conduite (par exemple évaluation des distances de sécurité en fonction de la vitesse, détection de trajectoires anormales et de freinage d'urgence).
[modifier | modifier le code]
Aux débuts de la navigation maritime côtière, les marins se repéraient grâce aux reliefs de la côte. Les éléments caractéristiques (villes, phares, églises…), appelés amers, sont toujours utilisés et permettent une localisation rapide et simple, facilement exploitable en cas de demande de secours (voir Navigation par relèvements).
La navigation au long cours est possible en utilisant les étoiles comme repère, c'est la notion de navigation astronomique ; elle était utilisée traditionnellement par les Polynésiens[7] (voir Peuplement de l'Océanie > Navigations austronésiennes). En Europe, elle a été rendue possible grâce au développement des horloges ; en effet, elle utilisait la position des astres, or celle-ci varie avec l'heure. Connaissant la date et l'heure, et muni d'une éphéméride (relevé des positions des étoiles selon la date et l'heure), les astres jouaient alors le même rôle que les repères côtiers.
La boussole permet de déterminer le cap que l'on suit, et pour un navire, la vitesse peut être estimée par la vitesse du vent et les courants. Ceci permet d'anticiper la trajectoire.
Pour se repérer, les aviateurs et marins naviguant aux instruments disposent des signaux émis par des antennes. À la fin des années 1960–début des années 1970, certains pays développent des réseaux d'antennes terrestres, comme le système de navigation Oméga ou bien le système LORAN-C. Puis, à la fin des années 1970 sont lancés des satellites (système GPS, GLONASS, futur système Galileo) . Les antennes émettent des signaux synchronisés, et le décalage entre la réception des signaux permet de déterminer la position sur le globe terrestre (voir Système de positionnement) ; ces systèmes sont également accessibles aux véhicules terrestres et aux piétons. Pour le décollage et l'atterrissage, les avions disposent de balises radio posées au sol leur donnant un repérage précis par rapport à la piste, permettant des manœuvres sans visibilité (de nuit ou par mauvais temps), voir les articles Vol aux instruments et VHF Omnidirectional Range.
Les systèmes de surveillance aérienne (tour de contrôle, aviation civile, armée) ou nautique (CROSS, centre régional opérationnel de surveillance et de sauvetage), ainsi que certains avions et navires, sont munis de radars. Ces dispositifs émettent une impulsion radio dans toutes les directions (en général avec une antenne tournante). Une impulsion revient si elle rencontre un obstacle ; le temps qu'elle met à revenir permet de déterminer la distance de l'obstacle, et le décalage en fréquence permet de déterminer la vitesse de l'obstacle (effet Doppler-Fizeau).
Notes et références[modifier | modifier le code]
- Pierre Varignon, Du mouvement en général par toutes sortes de courbes, & des forces centrales, tant centrifuges que centripètes, nécessaires aux corps qui les décrivent, Mémoires de l'Académie Royale des Sciences (MARS), 1700, Pag 83-101, Consulter l'article.
- Université en ligne, Mécanique.
- Vecteurs position, vitesse, accélération.
- Mécanique du point matériel, PDF sur les bases.
- Notons que cette notion est distincte de la notion de problème plan en statique.
- Repère de Frenet.
- Georges Boulinier et Geneviève Boulinier, « Les Polynésiens et la navigation astronomique », Journal de la Société des océanistes, t. 28, no 36, , p. 275–284 (lire en ligne)