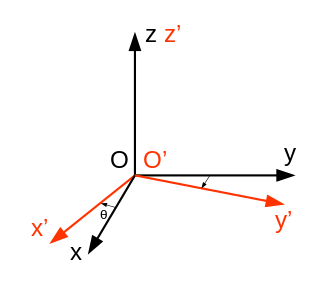
Groupe de Lorentz

Cet article est une ébauche concernant la relativité. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Le groupe de Lorentz est le groupe mathématique constitué par l'ensemble des transformations de Lorentz de l'espace de Minkowski.

Les formules mathématiques

• des lois de la cinématique de la relativité restreinte,
• des équations de champ de Maxwell dans le théorie de électromagnétisme,
• de l'équation de Dirac dans la théorie de l'électron,

sont toutes invariantes sous les transformations de Lorentz. En conséquence, le groupe de Lorentz exprimerait la symétrie fondamentale de plusieurs lois de la nature.

Le groupe de Lorentz affine

Le groupe de Lorentz complet ou inhomogène $R^4 \rtimes \operatorname{SO}_0(3,1)$ est un sous-groupe du groupe de Poincaré complet $R^4 \rtimes \operatorname{O}(3,1)$ qui réunit toutes les isométries affines de l'espace de Minkowski. Les transformations du groupe de Lorentz conservent non-seulement la forme quadratique $x^2+y^2+z^2-t^2$ forme de Lorentz de signature (3,1), mais aussi l'orientation des repères de l'espace de Minkowski.

En physique il s'agit des changements de référentiels de la relativité restreinte qui envoient un repère inertiel sur un autre, tout en conservant leur orientation aussi bien spatiale que temporelle. Ces transformations sont dites propres et orthochrones.

En mécanique quantique, c'est le groupe de Poincaré qui joue ce rôle : le temps peut alors être renversé (Symétrie T), ainsi que les coordonnées d'espace (Parité).

Le groupe de Lorentz linéaire

Le groupe de Lorentz $\operatorname{SO}_0(3,1)$ est un sous-groupe du groupe orthogonal $\operatorname{O}(3,1)$ qui réunit tous les automorphismes orthogonaux (applications linéaires bijectives) de l'espace vectoriel sous-jacent à l'espace de Minkowski. Le groupe de Lorentz linéaire est un groupe de Lie.

Remarque : Il existe plusieurs dénominations confuses de ces groupes. Par exemple en mécanique quantique, le groupe $\operatorname{O}(3,1)$ est parfois celui désigné par le terme de groupe de Lorentz, et le groupe des transformations propres et orthochrones $\operatorname{SO}_0(3,1)$, aussi noté $\operatorname{SO}^+(3,1)$ est alors appelé groupe de Lorentz restreint.

Articles connexes

• Groupe de Poincaré
• Relativité restreinte
• Covariance de Lorentz
• Invariance de Lorentz
• Équations de Maxwell