Masse
| Unités SI | kilogramme (kg) |
|---|---|
| Dimension | M |
| Nature | Grandeur scalaire conservative extensive |
| Symbole usuel | m ou M |
| Lien à d'autres grandeurs |
En physique, la masse est une grandeur physique positive intrinsèque d'un corps. On pensait traditionnellement qu'elle était liée à la quantité de matière contenue dans un corps physique, jusqu'à la découverte de l'atome et de la physique des particules. Il a été constaté que différents atomes et différentes particules élémentaires, ayant théoriquement la même quantité de matière, ont néanmoins des masses différentes. En physique newtonienne, c'est une grandeur extensive, c'est-à-dire que la masse d'un corps formé de parties est la somme des masses de ces parties. Elle est conservative, c'est-à-dire qu'elle reste constante pour un système isolé n'échangeant pas de matière avec son environnement. Dans le cadre du modèle standard de la physique des particules, la masse des particules résulte de leur interaction avec le champ de Higgs.
La masse se manifeste à travers deux propriétés fondamentales :
- en mécanique statique, c'est tout d'abord et historiquement une grandeur immédiatement accessible à la mesure, à travers la pesée, qui permet de comparer la masse d'une certaine quantité de matière à une masse étalon. C'est ce que l'on appelle la « masse pesante ». La masse est ainsi directement liée à la quantité de matière que contient un corps ;
- en mécanique dynamique, cette grandeur intervient directement dans le principe fondamental de la dynamique, comme exprimant la « résistance de la matière au changement de vitesse » : plus la masse du corps est importante, plus la force pour changer la direction ou la grandeur de sa vitesse doit être importante. C'est ce que l'on appelle la « masse inerte ». Cet aspect de la masse joue un rôle essentiel dans toutes les branches de la dynamique. C'est donc une notion présente dans de nombreuses relations de la physique classique et dans les calculs qui en découlent ;
- on constate une proportionnalité stricte entre masse inerte et masse pesante, indépendamment de la nature du matériau, ce qui permet de prendre la même unité pour les deux (et donc de les déclarer égales). Cette équivalence des deux notions a été érigée en un principe d'équivalence.
L'unité de masse est le kilogramme dans le Système international d'unités (SI).
Les termes masse et poids sont interchangeables dans la langue courante, mais en physique le poids est une grandeur différente (vectorielle et s'exprimant dans d'autres unités) : le poids d'un objet est la force de gravitation exercée sur cet objet par la Terre (ou, plus généralement, un corps céleste).
Grandeur physique[modifier | modifier le code]
Mesure[modifier | modifier le code]

Le moyen le plus commun de mesurer une masse est de la comparer à d'autres à l'aide d'une balance. En fait une balance compare des poids, le poids étant le produit de la masse par l'accélération de la pesanteur, dans un contexte où cette accélération peut être considérée comme constante. La mesure des masses se faisant usuellement au sein d'un fluide (l'air), en toute rigueur il faut aussi tenir compte de la poussée d'Archimède, qui est proportionnelle au volume et n'est donc pas la même pour deux corps de même masse mais de densités différentes. La correction est prise en compte pour les mesures très précises.
Avec l'émergence de la mécanique céleste au XVIIe siècle, il est devenu courant de mesurer les masses relatives des corps célestes. La masse n'est plus alors directement mesurée, mais calculée, à travers l'effet qu'elle exerce sur la trajectoire des autres corps. Cette masse, qui est statiquement à l'origine de la force de gravitation, est toujours une « masse pesante ». On peut de même estimer une masse par la perturbation du champ de gravité qu'elle induit. Cette mesure par gravimétrie n'est utilisable que pour les objets extrêmement lourds, et est utilisée en géologie pour estimer la taille d'une formation rocheuse, ainsi qu'en archéologie.
Mais par ailleurs, la cinématique a permis d'étudier les transferts de quantité de mouvement dus à des forces et se traduisant par des variations de vitesse. De même, avec la physique des particules du XXe siècle, la masse d'une particule chargée est calculée à partir de l'accélération qu'elle subit dans un champ électrique, ou de la courbure de sa trajectoire dans un champ magnétique. Cette masse qui apparaît en cinématique traduit la résistance de la matière à des changements de vitesse, et est la « masse inerte ». Il s'agit toujours d'une masse calculée à travers d'autres grandeurs physiques mesurées.
Au quotidien, la masse inerte en tant que « résistance de la matière aux variations de mouvement » se perçoit facilement à travers l'effet de forces continues, lorsque par exemple on souffle avec une paille sur une balle de tennis (de l'ordre de 57 g) et sur une boule de pétanque (de l'ordre de 800 g) : la force exercée dans les deux cas est sensiblement la même, mais il est beaucoup plus difficile de mettre en mouvement la boule de pétanque, car sa masse est beaucoup plus importante. De même, cette résistance se perçoit facilement à travers l'effet des chocs : un footballeur tapant dans un ballon de football (de l'ordre de 430 g) lui donne facilement une impulsion qui le fait partir à grande vitesse, sans que la quantité de mouvement de sa jambe n'ait sensiblement varié ; le même exercice sur un boulet de canon de même taille (dont la masse est d'une soixantaine de kilogrammes) n'ébranlera guère le boulet, mais arrêtera net la jambe (et très probablement, fracassera le pied).
Caractéristiques classiques[modifier | modifier le code]
La mécanique classique a dégagé un certain nombre de propriétés de la masse :
- Additivité : la masse d'un corps est la somme des masses de ses parties ;
- Mesure invariante : La masse d'un corps ne dépend pas du référentiel à travers lequel le corps est considéré ;
- Inertie : la masse se manifeste par la résistance qu'un corps offre à toute force provoquant une variation, en grandeur ou en direction, de sa vitesse. L'accélération subie a lieu dans la direction de cette force extérieure, et est inversement proportionnelle à la masse ;
- Pesanteur : deux corps massifs s'attirent en proportion de chacune de leur masse, suivant une force dirigée l'un vers l'autre le long de la ligne joignant leur centre de gravité, et en proportion inverse du carré de la distance qui les sépare. En particulier, l'attraction exercée par la Terre sur un corps est son poids ;
- Conservation : la masse d'un corps est conservée à travers tous les processus physiques ou chimiques auquel il est soumis.
Toutefois, la physique moderne montre que ces propriétés ne sont vérifiées que dans les conditions de l'expérience courante ; mais peuvent ne plus l'être en physique quantique ou en mécanique relativiste.
La masse est à la racine de deux grandeurs conservatoires fondamentales en mécanique :
- la quantité de mouvement, grandeur vectorielle multipliant la masse par le vecteur vitesse ;
- l'énergie cinétique, grandeur scalaire proportionnelle à la masse et au carré de sa vitesse.
Ces deux lois de conservation sont fondamentales tant en physique newtonienne qu'en physique moderne. Sur cette base, il est possible de proposer une nouvelle définition de la masse, qui permet de rendre compte des cinq propriétés ci-dessus sans en présupposer aucune ; en particulier sans avoir à recourir à la notion de force, critiquée au XIXe siècle par des physiciens comme Ernst Mach, Gustav Kirchhoff, Heinrich Hertz parmi d'autres.
Unité de masse[modifier | modifier le code]

Chaque culture a eu ses unités de masse, et des unités différentes étaient souvent utilisées pour des produits différents. Dans les anciennes unités de mesure françaises on peut relever les poids de marc, dont le quintal reste d'usage courant. Les unités de mesure anglo-saxonnes sont beaucoup plus variées, et la livre y reste d'usage courant. Il faut se rappeler que la livre, en France, n'avait pas la même valeur sur tout le territoire : la provençale, la parisienne ou encore la bretonne n'avaient pas tout à fait la même valeur et aujourd'hui encore, la livre tout comme le gallon n'ont pas la même valeur aux États-Unis et au Royaume-Uni. Beaucoup de marchandises se vendaient au volume, par boisseaux ou encore par barils, soit 18 boisseaux (235 litres) — différent du baril pétrolier qui ne fait que 158,98 litres.
L'unité SI de masse est le kilogramme (kg) et non pas[1] le gramme (g). On utilise également la tonne (t), égale à 1 000 kg.
Dans l'Union européenne, de nombreuses masses (et volumes) sur les produits de consommation sont indiquées en quantité estimée. Ils sont marqués comme tels, du symbole « ℮ » (U+202E), semblable à un e minuscule stylé.
Dans le domaine scientifique, on utilise l'unité de masse atomique. Du fait de l'équivalence masse-énergie révélée par la fameuse formule E=mc2, les physiciens spécialistes des particules utilisent la même unité de mesure pour la masse et l'énergie, en général un multiple d'électron-volt/c², ce qui est rendu indispensable par l'observation quotidienne, dans les accélérateurs de particules, de la transformation de l'énergie en ses différentes formes : masse, énergie cinétique, énergie de liaison, lumière.
Masse et poids[modifier | modifier le code]

On peut aussi estimer indirectement la masse à partir du poids, c'est-à-dire que l'on mesure la force qu'exerce l'objet à peser ; le dispositif est en fait un dynamomètre. C'est le cas le plus courant des pèse-personne et des balances électroniques. Cette méthode ne donne pas le même résultat de mesure sur la Terre et sur la Lune, parce que le dynamomètre compare le poids à une force indépendante de la gravitation (celle du ressort), alors que le poids, qui est la force de gravitation s'exerçant sur un corps donné, dépend du lieu, et sera différent sur Terre et sur la Lune. Pour mesurer correctement la masse d'un corps à partir d'un dynamomètre, il faut donc d'abord étalonner le dynamomètre avec une masse de référence.
Dans le langage courant, la masse est fréquemment confondue avec le « poids ». La confusion est d'autant plus facile que la graduation du peson est (incorrectement) donnée en kilogrammes, que c'est par une « pesée » que l'on mesure la masse, que cette pesée est (de fait) effectuée par une comparaison des poids, et que ce que les corps « pèsent » est donc (correctement) exprimé en kilogrammes.
Dans le vocabulaire de la physique, le mot « poids » désigne spécifiquement la force exercée par la gravité sur un corps pesant, dont la valeur dépend de la pesanteur, et dont l'unité est le newton (symbole N). On considère par exemple un objet de masse m suspendu à un dynamomètre. La Terre exerce sur cet objet une force , appelée poids de l'objet, qui est donnée par la loi universelle de la gravitation : en supposant la Terre parfaitement sphérique, le poids de l'objet est proportionnel à sa masse et inversement proportionnel au carré de sa distance au centre de la Terre. Donc, suivant l'altitude son poids est variable. Par exemple, à Paris, où g vaut 9,81 N/kg, une masse de 10 kg a pour poids 98 N (même si l'on dit couramment, dans la vie quotidienne, qu'un objet pèse 10 kg) ; au sommet de l'Everest, son poids est légèrement plus faible.

L'accélération de la pesanteur étant sensiblement constante sur la surface de la Terre, la mesure du poids rend compte de la masse pour les besoins pratiques, même s'il existe de légères différences d'un lieu à l'autre, de l'ordre du pour cent[a]. Pour cette raison, une unité pratique de poids a longtemps été le kilogramme-force, simplement défini comme le poids du kilogramme. La distinction entre poids et masse a conduit dans un souci de rigueur à remplacer dans l'affichage officiel le « kilogramme-force » par le « décanewton », qui n'est que 2 % plus élevé. Pour cette raison, les limites d'utilisation des engins de chantier et des ponts roulants sont souvent affichées en kilodécanewtons (kdaN), les opérateurs sachant qu'« en pratique » le kdaN correspond à une tonne (ou pour le dire en toute rigueur : c'est à 2 % près le poids d'une masse d'une tonne, dans des conditions normales de pesanteur).
À strictement parler, la masse se mesure avec une balance, tandis que le poids se mesure avec un peson. La meilleure manière de percevoir la différence est de se rappeler que la masse est une grandeur scalaire, un nombre sans orientation, tandis que le poids est une grandeur vectorielle, qui a une orientation vers le bas (et qui définit la verticale en un lieu). L'autre manière de visualiser la différence est de se remémorer la démarche embarrassée et flottante des astronautes sur la Lune : leur masse est la même que sur Terre, et se manifeste toujours par la même résistance aux variations de vitesse ; mais leur poids est six fois plus faible, à cause de la faible gravité lunaire.
Évolution historique du concept de masse[modifier | modifier le code]
En sciences physiques, on peut distinguer de nombreux aspects à travers lesquels apparaît la notion de masse, ou traduisant ce concept[2]. À ce jour, l'expérience montre que tous ces aspects conduisent à des valeurs identiques, l'ensemble construisant progressivement ce qu'est le concept abstrait de « masse » en physique.
Conception traditionnelle[modifier | modifier le code]

Depuis que le commerce existe, le « poids » d'un objet est ce qui permet d'apprécier une « quantité de matière », principe à la base de la vente par pesée : plus il y a de matière, et plus le prix à payer est fort ; plus le poids d'or est grand, et plus grande est sa valeur.
C'est cette notion qui conduit historiquement au premier concept de « masse », en tant que grandeur essentiellement additive (en termes modernes, une grandeur extensive). Pour l'expérience quotidienne, le champ gravitationnel terrestre est une donnée constante ; et il n'y a pas de raison de distinguer entre le poids concret, accessible aux sens, et une masse abstraite qui en serait la cause.

Pour la pensée scolastique, gouvernée par les enseignements d'Aristote, le poids est une qualité intrinsèque de la matière, laquelle est par nature attirée vers le bas parce que c'est son lieu de repos ; mais c'est une propriété des seuls corps lourds susceptibles de chuter[3] : l'air n'a pas de poids et reste à son emplacement, de même que les nuages. La loi empirique du mouvement est que tout corps tend vers son lieu de repos naturel, soit en tombant quand il est en l'air, soit en s'arrêtant progressivement quand il roule au sol : le mouvement résulte d'un déséquilibre, et le rétablissement de cet équilibre entraîne l'absence de mouvement. De plus, l'expérience courante montre que les objets lourds comme une enclume tombent rapidement, tandis que les objets plus légers, comme des plumes ou de la flanelle, tombent plus lentement ; ce qui conforte l'idée informelle que la vitesse de chute est qualitativement fonction du poids.
Nonobstant toutes sortes de transformations physiques et chimiques, la conservation de la masse a longtemps été expérimentalement observée, puis admise comme une grandeur fondamentale et confondue avec « la quantité de matière » (Isaac Newton l'a définie comme telle dans ses Principia Mathematica)[4]. La nature phénoménologique de la masse se confond dans cette approche avec celle du poids : c'est la qualité additive de la matière qui peut faire l'objet de comparaisons par pesée. L'opération de pesée conduira à terme à la notion de « masse pesante » (plus tard vue en mécanique newtonienne comme une « masse grave » puis une « masse gravitationnelle passive »), qui se mesure à travers la force appliquée à un objet lorsqu'il est passivement plongé dans un champ gravitationnel. Le rapport de cette « masse pesante » à celle d'une masse étalon peut être déterminé lors d'opérations de pesées classiques, parce que dans l'histoire de l'humanité, cette pesée est toujours effectuée dans le champ gravitationnel terrestre.
Mécanique galiléenne[modifier | modifier le code]
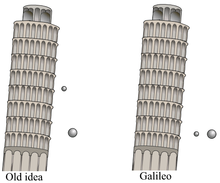
Avec la physique galiléenne, au début du XVIIe siècle, l'étude de la chute des corps et les premières études de dynamique permettent de dégager ce qui deviendra la notion de « masse inerte », qui est la mesure de la résistance interne d'un objet à un changement de mouvement[3] lorsqu'une force lui est appliqué.
La révolution introduite par Galilée est celle de la mesure des lois du mouvement. En pratique, dans ces premières expériences, la force en question est celle de la pesanteur, ou une fraction de celle-ci dans les expériences sur plan incliné ; et le mouvement étudié est celui d'un pendule ou d'un corps en chute libre. Expérimentalement, et contrairement à l'intuition de l'époque, la loi du mouvement ne dépend pas du poids — qui est pourtant de toute évidence la force à laquelle l'objet est soumis — et ne dépend pas non plus de la nature du corps ou de sa densité. Cette indépendance surprenante du résultat par rapport au poids a priori générateur du mouvement conduit à identifier dans la matière une qualité d'inertie, capacité du corps à s'opposer à la variation de vitesse en créant ce qui semble être une « force d'inertie » équilibrant l'effet du poids.
Par rapport à la vision scolastique, Galilée ne change donc pas radicalement la nature phénoménologique de la masse / quantité de matière, mais lui rajoute un caractère se manifestant dans les lois du mouvement : celui de pouvoir engendrer une « force d'inertie ». Pour Galilée, cette « force d'inertie », étant capable de rendre le mouvement indépendant du poids, se manifeste donc nécessairement de manière proportionnelle à celui-ci.

Galilée étudie des situations où le frottement est négligeable, ce qui condamne l'idée d'une tendance naturelle au repos. De toute évidence il n'y a pas une telle force d'inertie sur un corps au repos. Mais par ailleurs, cette « force d'inertie » se manifestant comme une opposition à toute variation de vitesse, le déplacement dans un plan horizontal, qui n'est pas influencé par le poids, doit donc également se faire sans variation de vitesse : ce déplacement idéal à vitesse constante, identifiée par Galilée, est celui d'un référentiel galiléen.
L'approche de Galilée était obscurcie par la confusion, traduisant les conceptions de son époque, entre la masse et le poids, ce dernier était compris comme une propriété (vectorielle) intrinsèque à la matière, et conduisant à l'idée d'une force compensatrice émergeant à l'occasion des variations de vitesse.
De nos jours, on dira plutôt que le poids est la manifestation d'une qualité de « masse pesante », tandis que la force d'inertie manifeste de son côté celle « masse inerte », l'une et l'autre propriétés scalaires intrinsèques de la matière, et que l'on trouve expérimentalement en proportion constante — ce qui permet d'assimiler l'une à l'autre. En termes modernes, l’expérience de Galilée est la première manifestation de l'identité entre masse inerte et masse pesante. Il y a cependant une différence conceptuelle très importante entre ces deux, parce qu'elles diffèrent radicalement dans leur manifestation. Conceptuellement, la « masse inerte » n'apparaît qu'en dynamique. Elle est définie en appliquant une force à un objet, et en mesurant l'accélération qui en résulte : à force égale, l'accélération d'un objet est inversement proportionnelle à la masse de cet objet.
Mécanique newtonienne[modifier | modifier le code]

Avec la mécanique newtonienne, à la fin du XVIIe siècle, la logique causale ayant conduit à imaginer une « force d'inertie » est inversée : dans la loi du mouvement il n'y a pas une « force d'inertie » découlant d'une qualité d'inertie (scalaire), qui s'oppose à la variation de vitesse que tend à créer la « masse pesante » (comprise comme vectorielle). L'approche analytique du calcul différentiel traite avant tout de position, de vitesse et d'accélération, et sépare alors ces questions de toute préoccupation relative à la masse.
Celle ci étant introduite, il apparaît que d'une manière générale, il est nécessaire d'appliquer une « force » pour créer une variation de vitesse en proportion de la quantité de matière, laquelle est alors mesurée par une « masse inerte » mi (comprise comme scalaire) ainsi mise en mouvement. Autrement dit, le changement de la quantité de mouvement d'un corps, provoqué par une force agissant sur lui, est proportionnel à cette force en grandeur et direction[3] ; ou inversement, une force est ce qui est capable de produire une variation de la quantité de mouvement d'un corps matériel. C'est le principe fondamental de la dynamique :
La nature phénoménologique de la masse inerte est donc de se manifester par le rapport entre une force appliquée et une variation de quantité de mouvement. Prise littéralement, cette définition que l'on note à présent est cependant circulaire[3], dans la mesure où la mesure d'une force suppose par ailleurs que la masse soit définie d'une manière ou d'une autre. Ce n'est qu'avec Ernst Mach que la masse inerte recevra une définition phénoménologique rigoureuse, à travers le principe d'action et de réaction.

Il n'y a pas non plus une qualité de poids (vectoriel) intrinsèque à la matière. L'approche newtonienne est que le poids (vectoriel) est également une force, qui traduit l'attraction qu'exerce la Terre, laquelle est proportionnelle à une certaine « masse grave » ; et seule cette « masse grave » (également comprise comme un scalaire) est une qualité intrinsèque à la matière, parce que la force, elle, doit dépendre de la distance à la Terre (ce que montrent les lois de Kepler). Pour la physique newtonienne, si les lois de la chute des corps sont les mêmes que celles de la mécanique céleste, et si donc la Lune « tombe » en permanence sur la Terre comme le ferait une pomme, c'est qu'il s'agit d'un seul et même phénomène : l'attraction subie par la Lune — ce qui mesure sa « masse pesante », mais dépend de sa distance — n'est autre que sa réponse gravitationnelle à la présence de la Terre (désignée dans ce contexte comme sa « masse grave », ou « masse gravitationnelle passive »). Ce changement de perspective conduit donc à identifier « masse grave » et « masse pesante ».
En séparant ainsi poids vectoriel et masse scalaire (qu'elle soit inertielle ou gravitationnelle), c'est Newton qui est ainsi à l'origine du concept moderne de masse scalaire[3]. Par ailleurs, la force exercée par la Terre sur une « masse grave » céleste est donc égale à celle nécessaire à vaincre la résistance à l'accélération de sa « masse inerte », ce qui conduit à supposer que « masse grave » et « masse inerte » sont de même nature, voire (dans la mesure où il n'y a pas de raison que les lois de la gravitation dépendent de la nature des corps) qu'elles sont égales.
Formalisé ensuite dans le cadre général du potentiel newtonien, la « masse gravitationnelle passive » devient une réinterprétation de la « masse pesante », qui prend sa source dans la loi universelle de la gravitation.
De son côté, la « masse gravitationnelle active » est la « charge massique » responsable du potentiel gravitationnel créé par un corps, et dont on constate la présence en mécanique céleste : pour Newton, « tous les corps ont en propre un pouvoir de gravité, proportionnel aux quantités de matière que chacun d'eux contient ». Autrement dit, la nature phénoménologique d'une masse (pesante), sur le plan de la mécanique céleste, est sa capacité à imposer une accélération centripète à son espace environnant ; cette capacité de « masse gravitationnelle active » se traduit par le « paramètre gravitationnel standard » , qui donne l'accélération gravitationnelle γ exercée par ce corps[b] à une distance r :
- , ou encore, sous forme vectorielle :
Par ailleurs, la distinction entre masses gravitationnelles active et passive n'a pas lieu d'être en mécanique classique, puisque la « charge massique » est aussi bien à l'origine du potentiel (donc de la masse active) qu'à l'origine de la force subie par une particule chargée qui y est placée (donc de la masse passive ou inertielle). Une différence entre ces deux notions n'apparaît qu'en relativité générale, dans certains problèmes de cosmologie.
Chimie et quantité de matière[modifier | modifier le code]

Pour Newton encore, la masse représente essentiellement une quantité de matière, qui est définie par le produit d'un volume (caractéristique géométrique) par une densité (propriété intrinsèque dépendant de la nature du matériau considéré)[3]. Un siècle plus tard, à la fin du XVIIIe siècle, Antoine Lavoisier découvre ensuite expérimentalement la loi de conservation de la masse : « la masse totale d'un système fermé reste constante quelles que soient les transformations physico-chimiques dont il peut être le siège ». De ce fait, c'est bien la masse qui est une qualité intrinsèque et conservatoire de la matière, et non la masse volumique.

Cette loi, qui se révéla approximative, confirmait la définition de la masse et permit de s'en servir comme constante dans les transformations chimiques (d'où la classification des éléments chimiques en fonction de leur masse atomique dans le tableau de Mendeleiev) et fut un élément de mesure permettant, entre autres, de mettre en évidence l'existence des atomes[4]. La notion de « quantité de matière » s'en est progressivement dégagée pour les besoins de la chimie. L'analyse précise des masses impliquées dans les transformations chimiques conduira à la loi des proportions définies, puis à la loi des proportions multiples, conduisant enfin à la notion d'atome et de masse atomique. La nature phénoménologique de la quantité de matière contenue dans un corps (chimiquement pur), qui se manifeste par la pesée, est alors essentiellement le nombre d'atomes (ou de molécules) impliqués, dont le nombre immense est appréhendé par le nombre d'Avogadro ; et la masse de ce corps n'est autre que la masse totale de ces atomes, agissant sur le plan pondéral par leur masse atomique.
Le Système international d'unités, continuellement amélioré depuis le XXe siècle, établit une distinction fondamentale entre la quantité de matière, mesurée en moles, et la masse, mesurée en kilogrammes.
La quantité de matière peut être déterminée avec précision dans certains cas, en comptant le nombre d'atomes d'un échantillon, obtenu par dépôt électrolytique ou par usinage d'ultra-haute précision d'un monocristal sans défaut. Une mesure précise montre que la masse d'un tel échantillon est « presque » intégralement due au nombre et à la nature des molécules qui le constitue. L'écart à cette valeur théorique est dû à l'énergie de liaison qui assure la cohésion de l'ensemble, et qui contribue à un léger « déficit de masse » de l'échantillon par rapport à la somme de ses constituants : c'est un effet abordé par la relativité restreinte.
Dans la vie de tous les jours, à notre échelle et lors de processus de basse énergie, on considère volontiers que la masse est une grandeur additive : si l'on prend deux paquets de sucre de 1 kg, on obtient 2 kg de sucre.
Relativité restreinte[modifier | modifier le code]

En relativité restreinte, cependant, la résistance d'un corps à une variation de vitesse devient d'autant plus grande que cette vitesse se rapproche de celle de la lumière : le principe fondamental de la dynamique reste valable sous sa forme , mais la « masse inerte » qui est définie ainsi ne peut plus être considérée comme constante ; elle ne se limite pas à la « masse au repos » de la matière, parce que l'énergie elle-même correspond à une masse inertielle, suivant le principe d'équivalence entre masse et énergie.
La masse d'inertie relativiste est alors définie par rapport à la masse au repos et la vitesse , par :

La masse au carré est l'invariant relativiste (la pseudo-norme) du quadrivecteur impulsion ou quadri-moment, , ce qui permet d'écrire la relation[c] , où est la masse au repos, E l'énergie totale du corps (énergie de masse + énergie cinétique) et p sa quantité de mouvement. Aussi, dans cette optique, il n'y a qu'une seule masse, la masse invariante, liée au quadri-vecteur énergie-impulsion[d]. Dès lors, on peut considérer la masse comme une forme d'énergie, appelée énergie de masse, et il apparaît que la notion véritablement invariante au cours des transformations physiques n'est pas la masse mais l'énergie qui se manifeste successivement sous différentes formes : sous forme de masse, d'énergie cinétique, d'énergie de liaison entre particules.

La conséquence de la théorie est que toute énergie possède également une masse inerte ; et inversement, toute masse au repos représente une énergie interne, susceptible d'être libérée. Dans les phénomènes usuels, les échanges d'énergie sont suffisamment faibles pour que la masse puisse être considérée comme sensiblement constante, mais ce n'est plus le cas pour la physique atomique et pour la cosmologie. La création de paires de particules élémentaires, et la fusion nucléaire, sont des exemples où des quantités non négligeables de masse sont converties en énergie, ou inversement. De même, la déviation gravitationnelle des rayons lumineux montre que des photons, particules sans masse mais porteur d'énergie, ont un comportement similaire à celui d'une masse gravitationnelle passive.
La relativité restreinte et la physique atomique révèlent que masse et quantité de matière sont deux quantités qui ne sont pas exactement proportionnelles ; bien que pour une substance inerte[e] donnée (le carbone par exemple), la masse est directement proportionnelle à la quantité de matière, aux forces de liaison près : dix grammes de carbone contiennent bel et bien dix fois plus de matière qu'un seul gramme de carbone. De ce fait, la masse n'est pas réellement une quantité extensive et conservatoire, mais doit être appréhendée dans un ensemble plus vaste. La relativité restreinte montre que la masse (inertielle) constitue une forme d'énergie du corps qui, dès lors, n'est pas strictement conservée : par exemple, la dissipation d'énergie sous forme lumineuse se traduit par une perte de masse qui n'est pas envisagée par la physique classique. La connaissance de la constitution de la matière offre d'autres exemples de pertes de masse par l'utilisation de l'énergie sous forme de liaisons atomiques.

L'énergie nucléaire, qu'elle provienne de la fusion ou de la fission, résulte de la transformation d'une certaine quantité de masse en énergie :
- quand un noyau de deutérium et un noyau de tritium fusionnent ensemble pour former un noyau d'hélium 4 (avec éjection d'un neutron), la masse finale est inférieure à la masse initiale ; la différence, ou défaut de masse, apparait sous forme d'énergie cinétique ;
- il arrive parfois que de la matière s'annihile au cours d'une transformation de masse en énergie. C'est le cas par exemple lorsqu'un électron entre en collision avec un positron : les deux particules disparaissent complètement et toute leur masse se transforme en rayonnement électromagnétique, sous forme de deux photons gamma hautement énergétiques (511 keV). Le phénomène inverse, la matérialisation de l'énergie par création de paires, est également possible.
Ce lien entre énergie et masse permet d'utiliser la même unité de mesure pour la masse et l'énergie : une unité de mesure de l'énergie, par exemple l'électron-volt est souvent utilisée pour exprimer la masse des particules élémentaires. Les accélérateurs de particules permettent de transformer physiquement de l'énergie en masse. Dans ce cadre, exprimer la masse en électron-volt permet de voir plus facilement dans quel régime d'énergie on se trouve et de savoir si l'on peut s'attendre à l'apparition de nouvelles particules. Par exemple, quand on accélère un électron jusqu'à 99,999 % de la vitesse de la lumière, on peut considérer que sa masse devient environ 224 fois plus grande qu'au repos. On peut alors affirmer que lors d'une collision d'un électron et d'un positron accélérés à 99,999 % de la vitesse de la lumière, on peut produire des muons, qui sont effectivement 206 fois plus massifs que des électrons.
Relativité générale[modifier | modifier le code]

La relativité générale posera comme principe qu'il n'est pas possible de distinguer une accélération reflétant un changement de vitesse d'une accélération gravitationnelle, ce qui revient à poser que par nature, la « masse inerte » est égale à la « masse grave ». La relativité générale dérive entre autres du principe d'équivalence qu'Einstein présente comme une « interprétation » de l'égalité de la masse inerte et de la masse grave en termes de relativité du mouvement accéléré.

La courbure de l'espace-temps est une manifestation relativiste de l'existence de la masse, et l'on peut considérer que la nature phénoménologique de la masse est sa capacité à courber l'espace-temps. Dans la métrique de Schwarzschild, la présence d'une masse se caractérise par la courbure qu'elle impose à l'espace, dont la déformation est donnée par le « rayon de Schwarzschild », ou rayon gravitationnel (formule où le facteur est la masse linéique de Planck) :
Pour les masses usuelles, cependant, cette courbure est très faible et difficilement mesurable ; c'est la raison pour laquelle elle n'a pas été découverte avant d'être prédite par la théorie de la relativité générale. À un facteur près, le rayon de Schwarzschild est lié au paramètre gravitationnel standard, noté , égal au produit de la constante gravitationnelle par la masse de l'objet correspondant. Là où le paramètre gravitationnel standard traduit la capacité d'une masse à imposer une accélération dans son environnement, le rayon de Schwarzschild traduit la capacité d'une masse à courber l'espace, parce qu'en relativité générale il n'y a pas de différence de nature entre ces deux manières de se placer dans un repère non galiléen.
La masse grave n'a pas sa place en relativité restreinte car la gravitation n'a pu y être incluse en respectant à la fois les principes relativistes et les observations. Toutefois, pour l'élaboration d'une gravitation relativiste, Einstein est parti du constat de l'égalité entre masse grave et masse inerte pour en tirer une « interprétation » sous la forme d'un nouveau principe : son « principe d'équivalence ». Ensuite, dans la théorie de la relativité générale, le rôle de la masse grave est tenu par l'énergie du corps, exprimée sous la forme du tenseur énergie-impulsion, prolongeant ainsi l'identité liant la masse inerte et l'énergie établie en relativité restreinte.
Mécanique quantique[modifier | modifier le code]

La masse des particules élémentaires (leptons et quarks) est une propriété intrinsèque de ces particules (qu'elle soit due ou non au boson de Higgs[réf. nécessaire]). Autrement dit, les particules élémentaires ont chacune une masse bien définie. Mais si macroscopiquement, la masse est associée à la matière, dans le détail la « matière » n'est pas un concept aussi bien défini que celui de « masse ». À l'échelle subatomique, non seulement les fermions (qui sont les particules usuellement associées à la notion de « matière ») ont une masse au repos, mais une masse au repos est également associée à quelques bosons, qui sont les particules vecteurs de force et qui servent de « colle » pour lier la matière. Un autre problème gênant pour assimiler masse et matière est qu'une grande partie de la masse au repos de la matière ordinaire provient de l'équivalent en masse d'énergies cinétiques, et de la contribution de particules qui n'ont pas par elles-mêmes de masse au repos. L'un dans l'autre, il n'y a que 1 % de la masse de la matière ordinaire qui peut être considéré comme provenant effectivement de la masse au repos de quarks fermioniques et d'électrons.
La masse, dans le cadre de la physique des hautes énergies, n'est pas une quantité extensive (additive). La masse de trois quarks pris individuellement, n'est pas égale à la masse d'un baryon contenant ces mêmes types de quarks : la masse du baryon résultant est égale à la somme des masses des trois quarks qui le constituent moins l'équivalent masse de l'énergie de liaison par la relation d'Einstein. C'est ainsi que les protons et les neutrons ont une masse (environ 940 MeV) bien différente de la somme des masses des quarks qui les composent (quark up et quark down) (d'environ 10 MeV). Dans cet exemple, la grande différence de masse indique que la force nucléaire entre les quarks est très grande : c'est l'interaction forte.
Sur le plan quantique, la masse se manifeste comme la différence entre la fréquence quantique d'une particule et son nombre d'onde. La masse quantique d'un électron, la longueur d'onde de Compton, peut être déterminée de diverses manières et est liée à la constante de Rydberg, le rayon de Bohr, et le rayon classique de l'électron. La masse quantique d'objets plus grand peut être mesurée directement au moyen d'une balance du watt.

La physique quantique utilise l'équivalence masse-énergie pour caractériser les particules virtuelles, responsables des interactions entre particules.
En mécanique quantique, l'action observable ne peut varier que par un nombre entier d'action élémentaire, la constante de Planck. Ce principe de base conduit à de nombreuses conséquences étranges sur les limites de l'observabilité, et au fait que les lois habituelles de la physique classique ne sont plus respectées à l'échelle quantique. Il existe en particulier une relation d'incertitude portant sur l'énergie d'une particule et la variable temps : la durée nécessaire à la détection d'une particule d'énergie à près vérifie la relation :
Inversement, donc, une fluctuation d'énergie ne peut pas être détectée physiquement si elle apparaît et disparaît en un intervalle de temps inférieur : le vide est constamment l'objet de fluctuations d'énergie extrêmement brèves. Ces fluctuations peuvent se matérialiser par la création de paires de particules / antiparticules, du moment que leur masse-énergie est inférieure à celle de la fluctuation, et que la paire s’annihile dans un temps inférieur à :
De même, une particule virtuelle peut être émise par une particule et capturée par une autre, à condition que ce soit fait suffisamment rapidement pour que la relation d'incertitude soit respectée. Ces particules virtuelles sont ainsi responsables des interactions entre particules (réelles), et de la propagation des champs ; ceci d'autant plus facilement que dans le monde étrange des particules virtuelles, la vitesse de la lumière n'est plus une limitation, du moment que leur durée de vie est négligeable. Ce concept de particule virtuelle est primordial en théorie quantique des champs.
En mécanique quantique relativiste, la masse est l'une des représentations irréductibles et unitaires d'énergie positive du groupe de Poincaré.
Boson de Higgs[modifier | modifier le code]

En particulier, le boson de Higgs, qui semble avoir été découvert le par l'expérience CMS et ATLAS au CERN, est, dans la théorie du modèle standard, considéré comme responsable de l'acquisition de masse par les particules.
En mécanique classique, la masse inerte apparaît dans l'équation d'Euler-Lagrange comme un paramètre m :
- .
En remplaçant le vecteur x par une fonction d'onde pour quantifier cette relation, ce paramètre m apparaît dans l'opérateur d'énergie cinétique :
- .
Dans la forme covariante (invariante par transformation relativiste) de l'équation de Dirac, et en unités naturelles, l'équation devient :
Bref, la masse m apparaît à présent comme une constante associée au quantum que décrit la fonction d'onde ψ associée à la particule.
Dans le modèle standard de la physique des particules élaboré à partir des années 1960, il a été proposé que ce terme constant pouvait provenir du couplage entre le champ ψ et un champ additionnel Φ, le champ de Higgs électrofaible. Dans le cas de fermions, le mécanisme de Higgs et al. conduit à remplacer dans le lagrangien le terme mψ par un terme de la forme .
Avec cette transformation, l’explicandum de pourquoi une masse est constatée sur diverses particules élémentaires se simplifie, la question étant alors celle de la valeur des couplages inconnus Gψ. Dans le modèle standard, un couplage des particules élémentaires au champ de Higgs permet alors d'expliquer l'origine de la masse de ces particules, une particule ayant fondamentalement une masse nulle par elle-même.
Du coup, le, ou les, boson(s) de Higgs serai(en)t responsable de la masse de toutes les particules élémentaires, ainsi que de celle de certains bosons d'échange des interactions. Au niveau des particules élémentaires, la masse des bosons de jauge de l'interaction faible (boson W et boson Z), est due au boson de Higgs, leur donnant ainsi des propriétés différentes de celles du boson de l'électromagnétisme, le photon.
L'existence du boson de Higgs a été confirmée de manière expérimentale en 2012 grâce à l'utilisation du LHC et a conduit à l'attribution d'un prix Nobel de physique en 2013[5]. Cette particule élémentaire constitue l'une des clefs de voûte du modèle standard de la physique des particules[6].
Cette découverte probable d'un boson de Higgs massif est considérée comme une confirmation forte de la théorie. Mais il y a de toute manière des arguments forts en faveur de la rupture de symétrie électrofaible telle que décrite par le mécanisme de Higgs et al. ; et la non-existence d'un tel boson de Higgs ne conduirait qu'à une description alternative (en) de ce mécanisme.
Identité de la masse inerte et de la masse grave[modifier | modifier le code]
Masse grave et masse inerte[modifier | modifier le code]
La masse d'un corps physique renvoie donc à deux natures phénoménologiques distinctes.
La masse grave (du latin gravis, lourd) est une propriété de la matière qui se manifeste par l'attraction universelle des corps, et au quotidien, par leur poids. Concrètement, en présence d'un même champ de gravité extérieur (celui de la Terre par exemple), la masse de 20 kg subira une force (le poids) deux fois plus élevée que la masse de 10 kg ; par ailleurs, une masse de 20 kg crée autour d'elle un champ de gravité deux fois plus intense qu'une masse de 10 kg. La masse grave (gravifique, gravitationnelle) d'un corps est définie par Isaac Newton comme une mesure de la quantité de matière de ce corps, c'est la grandeur physique intervenant dans le calcul de la force de gravitation créée ou subie par un corps : c'est ainsi qu'il l'a introduite dans la loi universelle de la gravitation, et qu'elle a été utilisée jusqu'à la relativité générale. La force de gravitation est donc proportionnelle à la quantité de matière. En physique classique, la masse grave est aussi supposée extensive.
La masse inerte est une propriété de la matière qui se manifeste par l'inertie des corps. Concrètement, une masse de 20 kg résiste deux fois plus à l'accélération qu'une masse de 10 kg. La masse inerte (inertielle) d'un corps est la grandeur physique utilisée pour calculer la force nécessaire pour qu'un corps acquière une accélération, en fonction de celle-ci. C'est la quantification de la résistance du corps aux accélérations. Mathématiquement, cela s'exprime par l'égalité , où est l'accélération acquise et est la force nécessaire à l'obtention de cette accélération. Isaac Newton a défini la masse inerte comme une autre mesure de la quantité de matière, et a considéré que pour imprimer à une quantité de matière doublée une même accélération, il fallait le double de force. En physique classique, la masse inerte est ainsi supposée extensive : en mêlant deux corps, on obtient un troisième corps dont la masse est la somme des masses des deux corps initiaux.
Charge d'un champ gravitationnel[modifier | modifier le code]

Il n'y a aucune raison fondamentale imposant que masse inerte et masse grave soient identiques, ce n'est qu'un fait empirique. À part le fait d'être toutes les deux proportionnelles à la quantité de matière (proportionnalité approximative, comme cela a été montré à partir du début du XXe siècle), la masse grave et la masse inerte semblent a priori n'avoir aucun lien entre elles, et constituer deux propriétés de la matière tout à fait indépendantes l'une de l'autre. Mais inversement, et bien que les deux soient conceptuellement distinctes, aucune expérience n'a jamais pu mettre en évidence une quelconque différence entre les deux.
Le fait de désigner ces deux manifestations sous le même terme de « masse » présuppose qu'il s'agit de la même grandeur physique, ce qui est effectivement la conception usuelle, mais obscurcit le caractère extraordinaire de cette proportionnalité. Pour mieux toucher du doigt cette différence, on peut discuter de deux qualités scalaires conservatoires et extensives de la matière, l'« inertie » qui se manifeste en dynamique, et le « pondéral » qui se manifeste par l'attraction gravitationnelle.

On peut en effet imaginer deux corps de natures différentes, ayant même inertie et des pondéraux différents. Le pondéral (qui intervient dans la loi de la gravitation de Newton) est formellement l'analogue de la charge électrique (qui intervient dans la loi de Coulomb) : le pondéral est en quelque sorte une charge gravitationnelle de la matière. De même qu'une charge électrique est à l'origine d'un potentiel électrostatique, le pondéral est à l'origine d'un potentiel gravitationnel. De même qu'une charge électrique placée dans un champ électrique subit une force électrostatique , de même une charge pondérale placée dans un champ gravitationnel subit une force de pesanteur . La particularité du pondéral est que contrairement à la charge électrique, ce scalaire est toujours positif, et la force d'attraction entre deux « charges gravitationnelles » de même signe est toujours positive.
Lorsqu'un corps subit une force électrostatique, du fait de sa charge électrique, il y répond par une accélération en raison inverse de son inertie ; mais il n'y a aucun rapport nécessaire entre cette inertie et sa charge électrique. Pour quelle raison l'inertie serait-elle alors toujours proportionnelle au pondéral, indépendamment de la nature des corps ? Puisque la masse inerte n'a aucun lien avec la charge électrique, pour quelle raison en aurait-elle un avec la masse grave ?
Détermination expérimentale de la proportionnalité[modifier | modifier le code]
L'équivalence entre masse inerte et masse grave est parfois appelé le « principe d'équivalence galiléen », ou encore la version faible du principe d'équivalence. La conséquence la plus directe de ce principe se rencontre en effet dans la loi de la chute libre, dont l'étude par Galilée l'avait conduit à dégager la notion d'inertie, étude à l'occasion de laquelle il avait pu constater que la loi de la chute était indépendante de la masse des corps et de leur nature. En termes modernes, si une masse pesante est placée dans un champ gravitationnel , elle subit une force , et y répond par une accélération , impliquant cette fois-ci sa masse inerte . Si l'expérience montre que la loi du mouvement est la même pour tous les corps, indépendamment de leur nature, c'est donc que l'accélération est la même pour tous, et donc :
Cette équation signifie que dire : « le rapport de la masse grave à la masse inerte est une constante »[b], est équivalent à dire que : « ils tombent suivant la même loi dans un champ gravitationnel donné ». Ce constat expérimental est effectivement ce qui permet d'énoncer une loi universelle de la gravitation.

Si les forces verticales sont équilibrées (à la balance) et que le rapport entre masse inerte et masse grave n'est pas constant, alors les forces horizontales seront déséquilibrées, se manifestant par un couple sur la balance de torsion.
Des expériences bien plus précises ont été réalisées par le baron Loránd Eötvös[7], en 1889, à partir d'une balance de torsion. L'idée à la base de son expérience est que le champ de pesanteur en un lieu sur Terre est (au premier ordre) la somme de deux composantes : une composante gravitationnelle, dépendant de la masse pesante et dirigée vers le centre de la Terre, et une composante centrifuge, dépendant de la masse inerte et dirigée perpendiculaire à son axe de rotation. Si donc masse inerte et masse pesante ne sont pas toujours strictement proportionnelles, la direction de la verticale doit être légèrement différente pour deux corps de nature différente. Dans ce cas, une balance de torsion dont le bras est orienté en est-ouest subira un couple tendant à le tourner au contraire dans l'orientation nord-sud, cet effet étant maximum aux latitudes de l'ordre de 45°. Avec cette méthode, Eötvös a pu montrer l'égalité des deux masses à 10−9 près.
Une autre démonstration de cette égalité se fonde sur la remarque que la loi du mouvement des corps en orbite dépend à la fois du paramètre gravitationnel standard et du rapport entre masse inerte et masse grave du satellite[b]. Le fait que tous les satellites autour de la Terre suivent le même mouvement démontre également l'égalité des deux masses ; de même, une inégalité se traduirait par un couple tendant à faire tourner les satellites hétérogènes, qui n'est pas non plus observé.
Même si ces deux grandeurs sont a priori conceptuellement distinctes, tous les résultats expérimentaux indiquent donc qu'elles sont toujours directement proportionnelles entre elles, avec un même coefficient de proportionnalité, pour toutes les matières expérimentées. À notre échelle, cette équivalence semble évidente, et l'égalité est aujourd'hui démontrée expérimentalement à 10-15 près.
En outre, dans ce cas, il n'y a pas de raison de considérer que masse inerte et masse grave sont deux grandeurs physiques indépendantes. Puisque le rapport entre elles est constant, c'est en fait la proportionnalité de ces grandeurs qui est vérifiée, indépendamment de la nature du corps. Dès lors, il s'agit d'une grandeur physique unique se manifestant par deux phénomènes différents, et un choix d'unité approprié permet de poser que l'« inertie » est égale au « pondéral », c'est-à-dire que masse inerte et masse grave sont identiques. On se permet dès lors de parler de la masse d'un corps : en choisissant la même unité de mesure pour les deux masses, leur universelle proportionnalité (expérimentale) se traduit par leur égalité.
Principe d'équivalence[modifier | modifier le code]
Ce fait d'expérience constitue le principe d'équivalence entre masse inerte et masse grave. Albert Einstein l'admit tel quel, et en donna une interprétation en termes de relativité du mouvement. Ce fut une avancée fondamentale vers la formulation des lois de la relativité générale. Albert Einstein développa la relativité générale en partant du principe que la correspondance entre masse inertielle et masse gravitationnelle (passive) n'était pas accidentelle, et que jamais aucune expérience ne pourrait détecter une quelconque différence entre les deux (c'est la version faible du principe d'équivalence). Cependant, dans le modèle théorique qui en résulte, la gravité n'est pas réellement une force, et ne répond pas au principe d'action et de réaction, si bien que « l'égalité de la masse inerte et de la masse gravitationnelle active […] demeure aussi étrange que jamais »[8].
Certaines théories scientifiques, comme la théorie des cordes, prédisent que l'équivalence pourrait cesser d'être vérifiée à des échelles beaucoup plus fines.
Dimensionnalités distinctes[modifier | modifier le code]
Même si masse inerte et masse grave sont expérimentalement égales, il est parfois utile, dans des problèmes d'analyse dimensionnelle, de faire comme si ces deux quantités pouvaient varier indépendamment et correspondaient donc à des dimensions différentes.
Comme signalé par ailleurs[b], la constante de gravitation G peut être vue comme un facteur d'échelle entre masse inertielle et masse grave ; on peut chercher comment un problème varie en fonction du rapport entre les forces de gravité (qui se traduisent par des mesures pondérales statiques) et les forces d'inertie. De manière imagée, cette analyse consiste à « faire varier la constante de gravitation » dans le problème. Plus pragmatiquement, elle consiste à distinguer, dans les équations aux dimensions, entre masse inerte et masse pesante.
Sur le plan des dimensions, la constante gravitationnelle est alors exprimée en . D'une manière générale, les unités « pondérales » se traduisent alors par des dimensions en masse pesante, alors que les unités « dynamiques » ou « énergétiques » se traduisent par de la masse inerte. L'analyse permet de proche en proche de distinguer entre ces dimensions pondérales et inertielles :
- la force donnée par est inertielle, exprimée en ;
- l'énergie est donc également purement inertielle, en : ce sera également le cas pour toutes les mesures thermiques, l'action, le couple, etc. ;
- de même, toutes les unités déterminées par des forces, comme la contrainte, dépendront de la masse inertielle ;
- c'est également le cas de toutes les grandeurs déterminées par la quantité de mouvement, comme le moment cinétique ;
- toutes les unités électriques sont déterminées par la force que subit tel ou tel conducteur, et les masses qui apparaissent dans ces unités sont donc également inertielles ;
- en revanche, des unités qui impliquent des pesées, comme la concentration massique ou le débit massique, sont bien des « masses pesantes ».
Masse et physique théorique[modifier | modifier le code]
Définition de Mach[modifier | modifier le code]
Dans l'histoire du concept de masse inerte, le chapitre le plus important est celui de la reformulation due à Ernst Mach, qui visait à éliminer de la définition les éléments qu'il qualifiait de « métaphysique » pour ne plus reposer que sur des phénomènes observables. En effet, dans la mécanique newtonienne, la force est définie par le produit de l'accélération et de la masse inerte, mais cette dernière n'est elle-même définie qu'à travers la force. La reformulation claire qu'il en donna est une définition considérée à présent comme « classique ». C'est à partir de cette définition que Albert Einstein a tenté de définir la masse dans sa théorie de la relativité générale, mais à son grand regret, l'approche de Mach ne peut pas se transposer en mécanique relativiste. L'approche de Mach est fondée sur le principe d'action et réaction, en appliquant le principe de proportionnalité entre accélérations pour définir le rapport entre masses sans avoir à passer par les forces en présence.
On considère un système isolé, constitué de deux corps (ponctuels) indicés « 1 » et « 2 », qui interagissent l'un sur l'autre. Quelle que soit la force agissant entre les deux corps, on peut observer expérimentalement que les accélérations subies par les deux corps sont toujours proportionnelles[f] et dans un rapport constant de l'un à l'autre :
Le point important est que ce rapport de proportionnalité est une constante qui ne dépend ni du temps, ni de l'état initial du système. La constante de proportionnalité est donc une propriété physique intrinsèque qui ne dépend que de ces deux corps ; et qui est modifiée lorsqu'on remplace l'un des deux corps par un troisième. On peut également noter que, d'après la définition :

On introduit à présent un troisième corps « 3 », et on refait les trois expériences correspondantes sur les trois couples possibles de masses ponctuelles (en supposant toujours le système isolé). On peut alors mesurer les trois constantes , et . On constate expérimentalement que l'on a toujours ou, autrement dit, que les coefficients vérifient une relation de transitivité . Cependant, dans cette dernière forme, on voit que le coefficient est le produit de deux termes, dont le premier, , ne dépend pas de la nature du corps « 3 » et le second, , ne dépend pas de celle du corps « 1 ». On en déduit que chaque coefficient s'exprime d'une manière générale comme le produit de deux termes, chaque terme ne dépendant que de la nature d'un des deux corps. On pose alors . Mais il faut que l'on ait de même, pour tout couple de corps a et b, et à chaque instant :
Par conséquent, on peut réécrire la proportionnalité des accélérations sous la forme suivante :
La quantité ainsi définie (à un facteur constant près, qui correspond au choix de l'unité de mesure) est appelée par définition « masse inertielle » de ce corps.
Il est donc possible de comparer la masse inertielle de deux corps, en mesurant les accélérations auxquelles ils sont soumis du fait de leurs interactions, sans avoir besoin de passer par les « forces » agissant sur ces deux corps (du moins, à condition de pouvoir supposer que le système est isolé, c'est-à-dire qu'il n'est pas soumis à des forces extérieures). Le rapport entre les deux masses est alors donné par le rapport des accélérations :
Masses négatives[modifier | modifier le code]

Que ce soit la « masse inerte » ou la « masse pesante », la masse est une grandeur physique qui apparaît toujours positive dans l'expérience courante. Cet état de fait empirique n'exclut pas que l'on puisse rencontrer un jour une masse négative, et n'interdit donc pas d'en explorer les propriétés sur le plan de la physique théorique, à défaut de pouvoir faire de la physique expérimentale. Des scientifiques se sont penchés sur la question car rien n'impose a priori que toute masse devrait être positive. En envisageant le concept de masse négative, il est important de considérer lequel des concepts de masse est négatif.
En physique théorique, une masse pesante négative est un concept hypothétique postulant l'existence de masse de « charge » négative, tout comme il existe des charges électriques positives et négatives. Comme rappelé ci-dessus, il n'y a pas de raison impérative, sur le plan théorique, pour que la masse inerte et la masse pesante soient systématiquement égales ; et la masse pesante peut être vue comme une « charge grave » gouvernant le mouvement de la matière dans un champ gravitationnel, de même qu'une « charge électrique » gouverne le mouvement de la matière dans un champ électrique. Dans ce cadre, et à partir du moment où l'on admet qu'une « charge grave » puisse être négative tout en maintenant une « inertie » positive, il ne peut rien y avoir d'intrinsèquement contradictoire dans les équations du mouvement.
Cependant, l'expérience montre que les « charges graves » de même signe s'attirent, la loi universelle de la gravitation imposant alors symétriquement que des « charges graves » de signe contraire se repoussent. Contrairement au cas électrique, une matière composite formée de « charges graves » positives et négatives ne peut donc pas maintenir sa cohérence, et les charges de différents signes tendent à la fois à se regrouper entre elles, et à se placer le plus loin possible de corps de charge contraire. Une « charge grave » de signe opposé ne peut donc que fuir un centre de masse homogène comme la Terre, le Soleil, la Galaxie. Dans le champ gravitationnel terrestre, par exemple, une « charge grave » de signe opposé sera soumise à une accélération donnée par :
- , conduisant à une loi de fuite à vitesse asymptotiquement constante.

C'est l'hypothèse d'une masse inertielle négative qui implique des formes contre-intuitives de mouvement. La principale caractéristique de la masse inertielle est en effet de permettre à la matière de stocker de l'énergie cinétique à travers une augmentation de la vitesse :
Une masse inertielle négative signifierait inversement qu'il faut fournir de l'énergie au système pour le ralentir, ou symétriquement, que le système fournit de l'énergie à son environnement en accélérant. Par exemple, un objet avec une masse inertielle négative accélérerait dans la direction opposée à celle vers laquelle il est poussé ou freiné. Une telle particule de masse inertielle négative serait par conséquent un projectile précieux : il fournit de l'énergie lorsqu'on lui donne une impulsion au départ, accélère sous l'effet des frottements de l'air, et en heurtant un obstacle tendrait donc à accélérer au travers de celui-ci, d'autant plus violemment que la résistance serait importante : un tel projectile serait donc irrésistible.
Tachyons et masses imaginaires[modifier | modifier le code]
L'idée initiale de tachyon dérive directement de l'équation donnant la masse relativiste : si une particule dépasse la vitesse de la lumière, son terme en devient un nombre imaginaire pur. Et, « par conséquent », une particule se déplaçant plus rapidement que la vitesse de la lumière « doit » avoir une masse imaginaire pure, le quotient des deux permettant de retrouver les lois usuelles sur l'énergie. Une telle approche littérale, cependant, n'a jamais été prise au sérieux, que ce soit en mécanique relativiste ou en mécanique quantique.
En mécanique quantique, on définit effectivement un champ tachyonique (ou plus simplement, un tachyon) comme un champ quantique associé à une masse imaginaire[9]. De fait, et bien que des tachyons (en tant que particules se déplaçant plus rapidement que la vitesse de la lumière) ne sont que des particules purement hypothétiques, et qui n'ont probablement pas d'existence réelle[9],[10], l'idée d'un champ associé à une masse imaginaire est cependant un concept important pour la physique moderne des particules[11],[12],[13], et ce concept est abordé dans des livres de vulgarisation de physique quantique[9],[14].
Dans ce cadre théorique, cependant, une excitation ne se propage jamais plus rapidement que la vitesse de la lumière. Qu'il puisse ou non exister des masses tachyoniques n'a aucune conséquence possible sur la vitesse de propagation de l'information, et il ne peut y avoir aucune violation du principe de causalité[15]. Même si le champ quantique comporte dans ce cas un terme qui peut être interprété comme une « masse imaginaire », aucune description de particule n'hérite d'une telle masse. Ce qui se traduit apparemment par une « masse imaginaire » montre par ailleurs que le système devient instable, et que cette instabilité conduit à une transition de phase, conduisant à un condensat de tachyons, très proche d'une transition de second ordre qui conduit à une symétrie brisée dans le modèle standard.
Notes et références[modifier | modifier le code]
- (it)/(en)/(de) Cet article est partiellement ou en totalité issu des articles intitulés en italien « Massa (fisica) » (voir la liste des auteurs), en anglais « Mass » (voir la liste des auteurs) et en allemand « Masse (Physik) » (voir la liste des auteurs).
Notes[modifier | modifier le code]
- Le poids d'un corps dépend aussi des forces d'inertie auxquelles il est soumis, comme la force centrifuge due à la rotation de la Terre, et à bien moindre niveau, des forces de marée.
- S'il faut cependant faire la distinction entre la masse inerte mi et la masse pesante mp, ce n'est pas l'accélération qui est donnée par le paramètre gravitationnel standard, mais la force de gravitation ; l'accélération qui s'en déduit étant de son côté donnée par . La formule exacte est donc , c'est-à-dire que l'accélération dépend bien du paramètre gravitationnel standard, mais également du rapport entre masse pesante et masse inerte du satellite. On voit au passage que la dimension de la constante gravitationnelle G est alors , c'est-à-dire que G apparaît comme un facteur de couplage entre masse inerte et masse pesante. Ces deux points ont d'importantes conséquences dans la discussion de l'équivalence (ou pas) entre masse inerte et masse pesante.
- En l'absence de champ électromagnétique ou de charge électrique. Dans le cas contraire il s'ajoute des termes aux niveaux de E et de p, et l'énergie E englobe alors l'énergie de masse, l'énergie cinétique et l'énergie électromagnétique du corps.
- On ne parle alors plus de masse au repos et de masse en mouvement. La relation relativiste amène certains auteurs à parler de la « masse au repos » et de la « masse en mouvement » ou « masse relativiste » , ce qui n'a pas de sens dans le cas où la masse est nulle car alors la particule (par exemple un photon) ne peut être au repos et ne peut avoir comme vitesse que celle de la lumière. D'autres considèrent que l'appellation de « masse » doit être réservée à la masse au repos, et que l'égalité ne permet que de parler d’énergie au repos et d’énergie à la vitesse v, « trouvant souhaitable que le mot masse s'applique à une propriété intrinsèque » du corps et sans lien avec sa vitesse, qui est relative au référentiel de l'observateur. C'est ainsi que James H.Smith explique son choix dans son livre Introduction à la relativité, édition Masson, 1997, préfacé par Jean-Marc Levy-Leblond. Ce choix est aussi celui de Lev Landau dans « Lev Landau et Evgueni Lifchits, Physique théorique [détail des éditions] ».
- Pour de l'uranium, une accumulation de matière peut donner une réaction modifiant la structure des atomes, et donc modifier la répartition de l'énergie entre masse et liaisons nucléaires.
- Pour que deux vecteurs soient proportionnels, ils doivent avoir la même direction, c'est-à-dire être colinéaires. Dans le cas exposé, les deux accélérations sont toujours dirigées le long de la droite joignant les deux masses ponctuelles.
Références[modifier | modifier le code]
- « Unité de masse (kilogramme) », sur le site du BIPM, bipm.org (consulté le ).
- (en) W. Rindler, Relativity : Special, General, and Cosmological, Oxford University Press, , 16–18 p. (ISBN 0-19-856731-6, lire en ligne).
- Masse, de Newton à Einstein. in Lecourt, Dominique (éd.), « Dictionnaire d'histoire et de philosophie des sciences », Presses universitaires de France, Paris, 1999.
- Article masse, rédigé par Michel Paty, dans le Dictionnaire d'histoire et philosophie des sciences, sous la direction de Dominique Lecourt, Éditeur PUF, 2006 (4e édition), (ISBN 2-13-054499-1).
- (en) « The Nobel Prize in Physics 2013 », sur nobelprize.org (consulté le ).
- « Le boson de Higgs, une énigme de la physique en passe d'être résolue », FranceTVinfo, (lire en ligne).
- (en) R. V. Eötvös, D. Pekár et E. Fekete, « Beiträge zum Gesetz der Proportionalität von Trägheit und Gravität », Annalen der Physik, vol. 68, , p. 11–66 (DOI 10.1002/andp.19223730903, Bibcode 1922AnP...373...11E).
- W. Rindler, op. cit., p. 22.
- Lisa Randall, Warped Passages: Unraveling the Mysteries of the Universe's Hidden Dimensions, p. 286 : « People initially thought of tachyons as particles travelling faster than the speed of light…But we now know that a tachyon indicates an instability in a theory that contains it. Regrettably for science fiction fans, tachyons are not real physical particles that appear in nature. »
- (en) Paul A. Tipler et Ralph A. Llewellyn, Modern Physics, New York, W.H. Freeman & Co., , 5e éd., 700 p. (ISBN 978-0-7167-7550-8), p. 54
« … so existence of particles v > c … Called tachyons … would present relativity with serious … problems of infinite creation energies and causality paradoxes. »
- (en) Kutasov, David, Marino, Marcos et Moore, Gregory W., « Some exact results on tachyon condensation in string field theory », J. High Energy Phys., vol. 0010, , p. 045 (DOI 10.1088/1126-6708/2000/10/045, Bibcode 2000JHEP...10..045K, arXiv hep-th/0009148).
- Sen, A. (2002), Rolling tachyon, J. High Energy Phys., 0204, 048, cité 720 fois au 2/2012.
- (en) G.W. Gibbons, « Cosmological evolution of the rolling tachyon », Phys. Lett. B, vol. 537, , p. 1–4 (DOI 10.1016/s0370-2693(02)01881-6, Bibcode 2002PhLB..537....1G, arXiv hep-th/0204008).
- Brian Greene, The Elegant Universe, Vintage Books, 2000.
- (en) Y. Aharonov, A. Komar et L. Susskind, « Superluminal Behavior, Causality, and Instability », American Physical Society, vol. 182, no 5, , p. 1400–1403 (DOI 10.1103/PhysRev.182.1400, Bibcode 1969PhRv..182.1400A).
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Dominique Lecourt et Thomas Bourgeois, Dictionnaire d'histoire et philosophie des sciences, Presses universitaires de France - PUF, coll. « Quadrige Dicos Poche », , 4e éd. (ISBN 978-2-13-054499-9). On y trouve, entre autres, l'article masse, rédigé par Michel Paty.
Articles connexes[modifier | modifier le code]
- Masse critique (réaction nucléaire)
- Pesanteur, poids, poids apparent
- Gravitation
- Concentration massique
- Masse volumique, masse surfacique et masse linéique
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Étienne Klein, E=mc2, sur lemonde.fr, [vidéo].
- Masse, de Newton à Einstein, dans Lecourt, Dominique (éd.), « Dictionnaire d'histoire et de philosophie des sciences », Presses universitaires de France, Paris, 1999.
- Jean-Marc Lévy-Leblond, Masse.
- Jacques Heurtaux, À propos de « masse inerte » et « masse de gravité », Revue française de pédagogie, 1978, vol. 45, no 1, p. 37-43.
- Damien Givry, Le concept de masse en physique : quelques pistes à propos des conceptions et des obstacles, Didaskalia, no 22, 2003, p. 41-67.

















































































