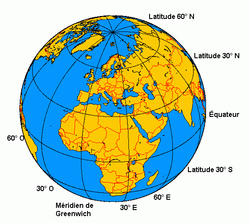
Latitude

La latitude est une coordonnée géographique représentée par une valeur angulaire, expression de la position d'un point sur Terre (ou sur une autre planète), au nord ou au sud de l'équateur qui est le plan de référence. La latitude est une mesure angulaire ; elle varie entre la valeur 0° à l'équateur et 90° aux pôles[n 1]. La latitude est utilisée en combinaison avec la longitude pour indiquer la position précise d'un élément sur Terre. Lorsqu'ils sont reliés entre eux, tous les endroits de la Terre ayant une même latitude forment un cercle dont le plan est parallèle à celui de l'équateur, d'où l'autre terme « parallèle » permettant de nommer une latitude.
La latitude est généralement notée φ (phi).
Définitions[modifier | modifier le code]
En géographie[modifier | modifier le code]
En géographie, il existe aujourd'hui, plusieurs définitions de la latitude, du fait que la Terre n'est pas parfaitement sphérique, mais que cette dernière est souvent comparée à un sphéroïde.
Historiquement, la première latitude inventée et exploitée par les Anciens[Qui ?] est la latitude astronomique. Les autres latitudes sont ensuite données sans ordre préétabli.
- La latitude astronomique d'un point est l'angle que fait la verticale du lieu en ce point avec le plan équatorial. C'est elle que l'on peut mesurer directement à partir d'observations (navigation astronomique, nivellement topographique).
- La latitude géodésique ou géographique ou ellipsoïdale d'un point est l'angle que fait la normale à l'ellipsoïde de référence en ce point avec le plan équatorial. C'est la latitude de la plupart des cartes.
- La latitude géocentrique d'un point est l'angle que fait une droite menée du centre de la Terre vers ce point avec le plan équatorial. Elle est surtout employée en astronomie. Elle peut s'écarter de la précédente de près de 11 minutes d'arc.
- La latitude géomagnétique d'un point correspond à la latitude corrigée en ce point par rapport à la position (actuelle) du pôle Nord magnétique, en place du pôle géographique. Elle sert notamment pour définir les zones où se produisent les perturbations électromagnétiques les plus sévères en cas d'orage magnétique, ainsi que pour positionner l'équateur magnétique (zone parcourue par les courants de l'électrojet équatorial)
- circumpolaire signifie autour des pôles Nord et Sud, c’est-à-dire à une latitude élevée.
Tous les endroits ayant une même latitude sont désignés collectivement sous le nom de parallèle géographique, car tous ces lieux sont placés sur une ligne parallèle à l'équateur. À l'inverse de la longitude dont la définition requiert le choix d'un méridien de référence, la latitude n'utilise donc que des références naturelles ou climatologiques.
Latitudes cartographiques[modifier | modifier le code]
D'autres latitudes existent, comme
- la latitude isométrique (en) ;
- la latitude réduite (en) ;
- la latitude croissante.
Ces trois latitudes sont employées dans la définition de projections cartographiques[1].
En géologie[modifier | modifier le code]
Les paléolatitudes désignent les latitudes de formation d'une roche. Il en existe potentiellement autant de sortes que de latitudes contemporaines. À partir de l'historique de position des pôles magnétiques dans l'histoire de la Terre, on peut reconstituer une paléolatitude non géomagnétique à partir d'une paléolatitude géomagnétique (mesure de paléomagnétisme). La différence entre la paléolatitude non-géomagnétique et la latitude actuelle est un signe de dérive des continents qui aide à reconstituer la carte du monde d'un autre temps.
La latitude astronomique aux origines[modifier | modifier le code]
La notion de latitude astronomique apparait dans l'Antiquité, chez les Grecs. Il est reconnu que c'est Eudoxe, au IVe siècle avant notre ère, qui le premier « découvrit » la latitude à partir des informations lues sur une méridienne astronomique[2].
Aujourd'hui, la latitude, pour une Terre supposée sphérique, est donnée à partir de formules simples de gnomonique[3].
Sur une méridienne, la hauteur théorique du Soleil, à midi, est de la forme :
où φ est la latitude du lieu et δ la déclinaison du Soleil dans son mouvement annuel.
Aux équinoxes, où δ = 0, on aura :

Au siècle d'Eudoxe, la division du cercle en 360° n'existe pas ; elle ne sera certaine que chez Ératosthène (276-195 avant notre ère). Aussi, la latitude (appelée climat dans l'Antiquité) s'exprime-t-elle par le rapport de la longueur du gnomon à son ombre ; ainsi, par exemple « En Grèce, la longueur du gnomon est à celle de l'ombre équinoxiale comme 4 est à 3[4]. », ce qui, en termes d'aujourd'hui, donne cotang φ = 4 / 3, ou plus simplement tan φ = 3 / 4 soit une latitude grossièrement égale à 37°.
Longueur d'un degré de méridien terrestre[modifier | modifier le code]
La longueur d'un degré de latitude varie un peu car la Terre n'est pas parfaitement sphérique : elle est légèrement aplatie aux pôles et renflée à l'équateur ; la longueur d'un degré d'arc de méridien terrestre, à même longitude, augmente ainsi légèrement de l'équateur (latitude = 0°) vers un pôle, nord (latitude = +90°) ou sud (latitude = -90°).
Elle varie cependant beaucoup moins que la longueur des degrés de longitude en fonction de la latitude ou distance à l'équateur, ainsi que le montre ce tableau :
| Longueur d'un degré de latitude |
Longueur d'un degré de longitude | |
|---|---|---|
| 0° | 110,574 km | 111,320 km |
| 15° | 110,649 km | 107,550 km |
| 30° | 110,852 km | 96,486 km |
| 45° | 111,132 km | 78,847 km |
| 60° | 111,412 km | 55,800 km |
| 75° | 111,618 km | 28,902 km |
| 90° | 111,694 km | 0,000 km |
Un algorithme de calcul est disponible auprès de la National Geospatial-Intelligence Agency (NGA)[5].
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Ou de 0 à 100 gon, exprimé en grades
Références[modifier | modifier le code]
- Didier Bouteloup, IGN, « Éléments de géométrie différentielle » [PDF], (consulté le )
- A. Szabo - E. Maula 1986, p. 14-23.
- Denis Savoie 2003, p. 41-42
- Rapporté d'Hipparque dans A. Szabo - E. Maula 1986, p. 17..
- Length of degree calculator - National Geospatial-Intelligence Agency
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- A. Szabo - E. Maula (trad. de l'allemand), Les débuts de l'astronomie, de la géographie et de la trigonométrie chez les Grecs, Paris, J. Vrin, coll. « L'histoire des sciences, textes et études », , 238 p. (ISBN 2-7116-0911-1).

- Denis Savoie, Les cadrans solaires, Paris, Belin, coll. « Pour la science », , 127 p. (ISBN 2-7011-3338-6).

Articles connexes[modifier | modifier le code]
- Longitude
- Lignes de latitude et longitude égales
- Déclinaison (astronomie)
- Ascension droite
- Parallèle
- Degree Confluence Project
- Mille marin
- Glossaire de la météorologie