Bouteille de Klein

En mathématiques, la bouteille de Klein (prononcé kla.in) est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein. Son nom provient possiblement d’une confusion ou d’un jeu de mots entre les termes Klein Fläche (« surface de Klein ») et Klein Flasche (« bouteille de Klein »)[1],[2],[3].
La bouteille de Klein est étroitement liée au ruban de Möbius et à des immersions du plan projectif réel telles que la surface de Boy. C'est un des exemples les plus simples de variété abstraite, car c'est une surface qui ne peut être représentée convenablement dans l'espace à trois dimensions. Mathématiquement, on dit qu'elle possède une immersion de classe C∞ dans l'espace ℝ3 de dimension trois, mais n'y possède pas de plongement continu.
Construction[modifier | modifier le code]
Il est impossible de représenter la bouteille de Klein dans l'espace ℝ3 (l'espace à 3 dimensions), sauf si l'on accepte qu'elle se traverse elle-même. Dans ℝ4, il est par contre possible de la réaliser sans auto-intersection (mathématiquement, on dit qu'elle possède un plongement (immersion injective) de classe C∞ dans ℝ4).
Voici un plan de montage dans ℝ3. À partir du carré initial, on colle les deux bords rouges l'un contre l'autre, dans le sens des flèches. La figure obtenue est un cylindre, dont on veut identifier les deux bords à l'aide des flèches bleues. Pour respecter le sens de ces flèches, il est nécessaire de retourner l'un des cercles avant de le recoller à l'autre, et pour cela, d'opérer une auto-intersection.
Si les deux segments bleus étaient orientés de la même façon, le recollement des segments opposés donnerait un tore. Si au contraire, les deux segments rouges étaient orientés en sens inverse comme les deux segments bleus, le recollement des segments opposés donnerait un plan projectif.
Autre méthode de construction[modifier | modifier le code]
La bouteille de Klein peut aussi être obtenue par recollement de deux rubans de Möbius le long de leurs bords. De manière équivalente, la bouteille de Klein est la somme connexe de deux plans projectifs.
On se donne deux exemplaires d'un tel carré, et on obtient deux exemplaires de ruban de Möbius en faisant cette fois d'abord l'identification suivant les flèches bleues. Chacun de ces rubans a alors un seul bord : les côtés verticaux rouges qui ont été connectés à la suite de l'identification précédente ; recoller les deux rubans suivant leurs bords peut alors être considéré comme équivalent à recoller le bord droit du second carré, au bord gauche du premier, et vice-versa. On voit aisément qu'on retrouve alors bien le cylindre, mais avec l'identification des bords bleus déjà effectuée, c'est-à-dire la bouteille de Klein.

Il est peut-être plus facile de voir qu'une bouteille de Klein coupée en deux dans le sens de la hauteur fournit bien deux rubans de Möbius.
Paramétrisation[modifier | modifier le code]
La paramétrisation de l'immersion dans trois dimensions de la bouteille de Klein vue précédemment s'obtient comme suit : est un paramètre qui suit le corps de la bouteille tandis que évolue le long de sa section.
[Information douteuse][réf. nécessaire]
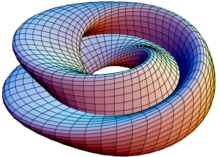

Une paramétrisation plus simple s'obtient de la façon suivante, donnant une immersion en « 8 » de la bouteille de Klein. Elle consiste à prendre une courbe en forme de 8 dans un plan vertical, et à lui faire effectuer un tour complet autour de l'axe Oz pendant que le 8 lui-même effectue un demi-tour. Cette construction est comparable à celle du ruban de Möbius, où le segment pivotant est remplacé par le 8. La bouteille de Klein est alors formée à partir d'un cylindre dont la base est en forme de 8, les deux bases opposées étant recollées de façon compatible avec leur orientation.
Dans cette immersion, l'auto-intersection est un cercle inscrit dans le plan Oxy. La constante positive est le rayon de ce cercle. Le paramètre donne l'angle dans le plan Oxy et est un paramètre définissant la section de la figure en forme de 8.
Propriétés[modifier | modifier le code]
- La bouteille de Klein est la somme connexe de deux plans projectifs réels.
- En la coupant en deux par rapport à son plan de symétrie, on obtient deux fois un ruban de Möbius.
- Sa caractéristique d'Euler-Poincaré est nulle.
- Ses nombres de Betti non nuls sont b0 = 1 et b1 = 1.
- Son nombre chromatique est 6.
- Son groupe fondamental (qu'on peut calculer[4] en considérant la bouteille comme un CW-complexe, ou comme un quotient du plan ou du tore, ou comme l'espace total d'une fibration en cercles sur le cercle) est le produit semi-direct de ℤ par lui-même donné par la présentation 〈a, b | aba−1b〉.
- D'après le théorème d'Hurewicz, son premier groupe d'homologie en est l'abélianisé. C'est donc le produit direct ℤ×ℤ2.
- La bouteille de Klein possède un revêtement orientable à deux feuillets, difféomorphe au tore.
Dans la culture populaire et dans l'art[modifier | modifier le code]

- La bouteille de Klein fait l'objet d’un chapitre (XII) dans La Potière jalouse de Claude Lévi-Strauss (édition Plon 1985) : interprétations psychanalytiques et champ sémantique des orifices corporels.
- Une des devises shadoks (« s’il n’y a pas de solution c’est qu’il n’y a pas de problème ») comporte une bouteille de Klein dans son illustration, elle symbolise un problème impossible à résoudre.
- Dans le dessin animé Futurama, une marque de bière, « Klein’s Beer », est vendue dans des bouteilles de Klein.
- Dans le jeu vidéo NetHack, tenter de verser une potion dans elle-même produit le message suivant : « That is a potion bottle, not a Klein bottle! » (« C’est une bouteille de potion, pas une bouteille de Klein ! »)
- Dans le jeu Magic: The Gathering, une carte s'appelle « Elkin Bottle »[5] (Ère Glaciaire, en 1995) en hommage à Richard Garfield, inventeur du jeu et mathématicien de son état. Les concepteurs ont transformé le nom, « Elkin » étant une anagramme de « Klein ».
- Dans le musée du quai Branly, l'image de la bouteille de Klein était explicitement citée dans un panneau pour expliquer la vision de la sexualité dans les civilisations dites primitives. L'homme parfait est perçu comme un individu dont les parties reproductives se confondent avec l'intérieur de la bouche si bien que cet homme n'a ni intérieur ni extérieur. Pour appuyer le discours, le visiteur pouvait remarquer la présence de la bouteille de Klein en verre (voir photo ci-contre). Ce panneau n'est plus visible au musée actuellement.
- Dans le roman Le Sixième Sommeil de Bernard Werber, la bouteille de Klein est une des manières pour le héros, Jacques Klein, de pénétrer dans une nouvelle dimension du sommeil.
- En 2014, l'artiste Gary Hill réalise Klein Bottle with the Image of Its Own Making (after Robert Morris) consistant en une bouteille de Klein transparente posée sur un socle dans laquelle est projeté une vidéo faisant référence au titre[6].
- Dans son installation Bonbons très bons[7] de 1993, l'artiste français Fabrice Hybert a intégré une bouteille de Klein en verre dont une partie reprend la forme d'un estomac.
- Dans la sixième partie du manga JoJo's Bizarre Adventure, Stone Ocean, l'antagoniste Enrico Pucci fait référence à la bouteille de Klein et au ruban de Möbius.
- Nommé une fois par Ritsuko Akagi, la chef scientifique de la NERV, dans l'épisode 20 de Neon Genesis Evangelion « Forme du cœur, miroir des gens ».
Notes et références[modifier | modifier le code]
- Ian Stewart, 17 équations qui ont changé le monde, Éditions Robert Laffont, , 416 p. (ISBN 978-2-221-13334-7 et 2-221-13334-X, lire en ligne), p. 135.
- (en) Francis Bonahon, Low-dimensional Geometry : From Euclidean Surfaces to Hyperbolic Knots, Providence, R.I., AMS Bookstore, , 384 p. (ISBN 978-0-8218-4816-6, présentation en ligne), p. 95.
- (de) « Klein'sche Flasche », sur vismath.eu (consulté le ).
- (en) Allen Hatcher, Algebraic Topology, CUP, (ISBN 978-0-521-79540-1, lire en ligne).
- Site magiccorporation.
- (en) « Klein Bottle with the Image of Its Own Making (after Robert Morris) », sur portlandartmuseum.us (consulté le )
- « Bonbons très bons (Fabrice Hyber) - atlasmuseum », sur publicartmuseum.net (consulté le )
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Équations et représentations de bouteilles de Klein
- www.klein-bottle-film.com: Animation de la Bouteille de Klein de 2010: Un voyage en voiture virtuel par la Bouteille de Klein et une description originale de Felix Klein - une animation fait à la Freie Universität Berlin.
- Bouteille de Klein sur le glossaire du site Publimath
- [vidéo] Disponible sur YouTube












