Correspondance AdS/CFT

Un article de Wikipédia, l'encyclopédie libre.

En physique théorique, la correspondance anti de Sitter/théorie conforme des champs (en anglais : anti-de Sitter/conformal field theory correspondence, d'où son abréviation en correspondance AdS/CFT) est une conjecture reliant deux types de théories. Les théories conformes des champs (CFT) occupent un côté de la correspondance ; ce sont des théories quantiques des champs qui incluent des théories similaires à celles de Yang-Mills qui décrivent les particules élémentaires. De l'autre côté, les espaces anti de Sitter (AdS) sont des théories de gravité quantique, formulées en termes de théorie des cordes ou de théorie M. La correspondance est également appelée parfois dualité de Maldacena ou dualité jauge/gravité.

La dualité représente une avancée majeure dans la compréhension de la théorie des cordes et de la gravité quantique[1] car elle fournit une formulation non-perturbative (en) de la théorie des cordes avec certaines conditions aux limites et parce qu'elle est la réalisation la plus réussie du principe holographique, un concept de gravité quantique proposé à l'origine par Gerard 't Hooft puis amélioré et mis en avant par Leonard Susskind.

Elle fournit également un outillage puissant pour étudier les théories quantiques de champs fortement couplés[2]. L'intérêt de la dualité provient essentiellement du fait qu'il s'agit d'une dualité forte/faible : quand les champs de la théorie quantique interagissent fortement, ceux de la théorie gravitationnelle interagissent faiblement et peuvent ainsi être plus facilement appréhendés mathématiquement. Ceci a permis d'étudier des aspects complexes de la physique nucléaire et de la physique de la matière condensée en les traduisant en termes de théorie des cordes, plus aisés.

La correspondance AdS/CFT est proposée pour la première fois par Juan Maldacena à la fin 1997. Des aspects importants sont élaborés dans des articles de Steven Gubser (en), Igor Klebanov (en) et Alexander Polyakov, et Edward Witten. En , l'article de Maldacena approche les 15 000 citations, ce qui en fait l'article le plus cité dans le domaine de la physique des hautes énergies[3].

Contexte[modifier | modifier le code]

Gravité quantique et cordes[modifier | modifier le code]

Articles détaillés : Gravité quantique et Théorie des cordes.

La compréhension actuelle de la gravitation est basée sur la relativité générale. Formulée en 1916 par Albert Einstein, la relativité générale explique la gravitation en termes de géométrie de l'espace et du temps (ou espace-temps). Elle est formulée dans le langage de la physique classique[4] développé par des physiciens comme Isaac Newton et James Clerk Maxwell. Les autres forces non-gravitationnelles sont expliquées dans le cadre de la mécanique quantique. Développée dans la première moitié du XXe siècle par un certain nombre de physiciens, la mécanique quantique décrit les phénomènes physiques de façon radicalement différente, sur la base de probabilités[5].

La gravité quantique est la branche de la physique qui cherche à décrire la gravitation en utilisant les principes de la mécanique quantique. Actuellement, l'approche la plus populaire est la théorie des cordes[6], qui modélise les particules élémentaires non pas comme des points sans dimension mais comme des objets à une dimension appelés des cordes. Dans la correspondance AdS/CFT, on prend en compte typiquement les théories de gravité quantique dérivées de la théorie des cordes ou de son extension moderne, la théorie M.

Dans la vie courante, il existe trois dimensions d'espace familières (haut/bas, gauche/droite, avant/arrière) et une dimension de temps. Ainsi, dans le langage de la physique moderne, l'espace-temps est dit à quatre dimensions[7]. L'une des particularités de la théorie des cordes et de la théorie M est qu'elles nécessitent des dimensions supplémentaires d'espace-temps pour leur cohérence mathématique : l'espace-temps de la théorie des cordes est à 10 dimensions, celui de la théorie M à 11 dimensions[8]. Les théories de gravité quantique apparaissant dans la correspondance adS/CFT sont typiquement obtenues grâce à un procédé appelé compactification (en), produisant un espace-temps au nombre de dimensions réduit, les dimensions supplémentaires étant « enroulées » en cercles[9].

Une analogie courante pour la compactification est de considérer un objet multidimensionnel comme un tuyau d'arrosage. Vu d'assez loin, il semble n'avoir qu'une dimension, sa longueur, mais en s'en approchant on découvre qu'il possède une autre dimension, sa circonférence. Une fourmi se déplaçant sur sa surface intérieure bougerait en deux dimensions[10].

Théorie quantique des champs[modifier | modifier le code]

Articles détaillés : Théorie quantique des champs et Théorie conforme des champs.

L'application de la mécanique quantique aux objets physiques tels que le champ électromagnétique, qui s'étendent dans l'espace et le temps, est appelée théorie quantique des champs[11]. En physique des particules, les théories quantiques des champs forment la base de la compréhension des particules élémentaires, qui sont modélisées comme excitations de champs fondamentaux. Les théories quantiques des champs sont également utilisées en physique de la matière condensée pour modéliser des objets ressemblant à des particules, des quasi-particules[12].

La correspondance AdS/CFT prend en compte certaines formes de théories quantiques des champs appelées théories conforme des champs. Il s'agit de formes particulières, symétriques et mathématiquement bien formées, de théories quantiques des champs (elles sont caractérisées par leur invariance (en) lors de transformations conformes). Ces théories sont souvent étudiées dans le contexte de la théorie des cordes, où elles sont associées à la surface décrite par une corde se propageant dans l'espace-temps, et en physique statistique, où elles modélisent des systèmes à un point critique[13].

Présentation de la correspondance[modifier | modifier le code]

Géométrie d'un espace anti de Sitter[modifier | modifier le code]

Article détaillé : Espace anti de Sitter.
Un espace anti de Sitter tridimensionnel ressemble à un empilement de disques hyperboliques, chacun représentant l'état de l'univers à un instant donné. L'espace-temps résultant ressemble à un cylindre solide.

Dans la correspondance AdS/CFT, on considère la théorie des cordes ou la théorie M sur un fond anti de Sitter, c'est-à-dire que la géométrie de l'espace-temps est décrite en termes d'une certaine solution de vide (en) de l'équation d'Einstein appelée espace anti de Sitter[14].

En termes très généraux, un espace anti de Sitter est un modèle mathématique d'espace-temps où la notion de distance entre les points (la métrique) est différente de celle en géométrie euclidienne ordinaire. Elle est fortement liée à un espace hyperbolique, qui peut être vu comme un disque tel qu'illustré sur la droite[15]. Dans cette image, un disque est pavé par des triangles et des carrés. Il est possible de définir une distance entre les points de ce disque telle que tous les triangles et carrés aient la même taille et que la frontière circulaire extérieure soit infiniment loin de tout point de l'intérieur[16].

Si on empile des disques hyperboliques représentant l'état de l'univers à un instant donné, l'objet géométrique résultant est un espace anti de Sitter tridimensionnel[15]. Il ressemble à un cylindre dont chaque section est une copie du disque hyperbolique. Dans la figure ci-contre, le temps s'écoule le long de la verticale. La surface du cylindre joue un rôle important dans la correspondance AdS/CFT. Tout comme le plan hyperbolique, l'espace anti de Sitter est incurvé de telle façon que tout point de son intérieur est infiniment éloigné de la surface. La relation mathématique entre l'intérieur et la surface d'un espace anti de Sitter est liée à la construction ambiante (en) de Charles Fefferman et Robin Graham[17],[18].

Cette construction décrit un univers hypothétique possédant seulement deux dimensions d'espace et une dimension de temps, mais elle peut être généralisée à un nombre arbitraire de dimensions[15].

Le concept d'AdS/CFT[modifier | modifier le code]

Une caractéristique importante d'un espace anti de Sitter est sa frontière (qui ressemble à un cylindre dans le cas d'un espace tridimensionnel). L'une des propriétés de cette frontière est que, localement autour de chaque point, elle ressemble à un espace de Minkowski, le modèle d'espace-temps utilisé en physique non-gravitationnelle[19].

Il est alors possible de considérer une théorie auxiliaire où l'« espace-temps » est donné par la frontière de l'espace anti de Sitter. Cette observation est le point de départ de la correspondance AdS/CFT, qui déclare que la frontière d'un espace anti de Sitter peut être vue comme l'« espace-temps » d'une théorie conforme des champs. La correspondance affirme que cette théorie conforme des champs est équivalente à une théorie gravitationnelle sur le volume de l'espace anti de Sitter, dans le sens qu'il existe un « dictionnaire » traduisant les calculs d'une théorie en calculs de l'autre. Chaque entité d'une théorie a son équivalent dans l'autre théorie. Par exemple, une particule de la théorie gravitationnelle correspond à un ensemble de particules sur la théorie frontière. De plus, les prédictions des deux théories sont quantitativement identiques : si deux particules ont 40 % de chances d'entrer en collision dans la théorie gravitationnelle, alors les ensembles correspondants dans la théorie frontière ont également 40 % de chances d'entrer en collision[20].

La frontière d'un espace anti de Sitter a moins de dimensions que l'espace anti de Sitter lui-même. Par exemple, dans l'exemple tridimensionnel illustré plus haut, la frontière est une surface à deux dimensions. La correspondance AdS/CFT est souvent décrite comme une « dualité holographique » car cette relation entre les deux théories est similaire à la relation entre un objet tridimensionnel et son image par holographie[21] : bien qu'un hologramme soit bidimensionnel, il porte encore l'information des trois dimensions de l'objet qu'il représente. De façon similaire, les théories qui sont liées par la correspondance AdS/CFT sont conjecturées comme étant exactement équivalentes, bien qu'existant dans un nombre de dimensions différent. La théorie conforme des champs est comme un hologramme qui capture l'information d'une théorie de gravité quantique possédant plus de dimensions[16].

Exemples[modifier | modifier le code]

À la suite de l'idée de Maldacena en 1997, les théoriciens ont découvert plusieurs réalisations de la correspondance AdS/CFT, reliant diverses théories conformes des champs à des compactifications de théorie des cordes ou de théorie M dans un nombre de dimensions varié. Les théories impliquées ne sont généralement pas des modèles viables du monde réel, mais possèdent certaines propriétés qui les rendent utiles pour résoudre des problèmes en théorie quantique des champs et en gravité quantique (elles impliquent typiquement des supersymétries ou un nombre de dimensions d'espace-temps sans sens physique).

L'exemple le plus connu conjecture que la théorie des cordes de type II sur l'espace produit AdS5×S5 est équivalente à la théorie super Yang-Mills N=4 (en) sur sa frontière à quatre dimensions[22],[23],[24]. Dans cet exemple, l'espace-temps de la théorie gravitationnelle est effectivement à cinq dimensions (d'où la notation AdS5) et il existe cinq dimensions additionnelles « compactées » (notées par S5) ; le monde réel possédant quatre dimensions — au moins macroscopiquement —, cette version de la correspondance n'est pas un modèle réaliste de la gravité. De même, la théorie duale n'est pas un modèle viable car elle suppose une supersymétrie étendue (plus précisément, c'est une théorie de Yang-Mills supersymétrique sur l'espace R4 avec supersymétrie étendue N=4 et groupe de jauge U(N)). Néanmoins, cette théorie frontière partage certaines caractéristiques avec la chromodynamique quantique, la théorie décrivant l'interaction forte : elle décrit des particules similaires aux gluons de la chromodynamique quantique ainsi que certains fermions[6]. En conséquence, elle a trouvé des applications en physique nucléaire, particulièrement dans l'étude du plasma quark-gluon[25],[26].

Une autre réalisation affirme que la théorie M sur AdS7×S4 est équivalente à la (2,0)-théorie en six dimensions[22]. Dans cet exemple, l'espace-temps de la théorie gravitationnelle est à 7 dimensions. L'existence de la (2,0)-theorie est prédit par la classification des théories super conformes des champs (en). Elle est mal comprise car il s'agit d'une théorie quantique sans limite classique[27]. Malgré la difficulté d'étude, elle est considérée comme un objet intéressant pour un certain nombre de raisons, à la fois physiques et mathématiques[27],[28].

Une troisième réalisation fait correspondre la théorie M sur AdS4×S7 et la théorie super-conforme ABJM en trois dimensions[29]. La théorie gravitationnelle possède ici quatre dimensions non-compactes, cette version de la correspondance fournissant une description plus réaliste de la gravité[29].

Applications à la gravité quantique[modifier | modifier le code]

Formulation non-perturbative de la théorie des cordes[modifier | modifier le code]

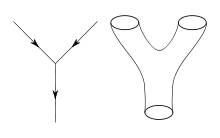
Interaction dans le monde quantique : lignes d'univers de particules ponctuelles ou feuilles d'univers parcourues par des cordes fermées.

En théorie quantique des champs, on calcule typiquement les probabilités d'événements physiques en utilisant les techniques de la théorie des perturbations. Développée entre autres par Richard Feynman dans la première moitié du XXe siècle, elle utilise des diagrammes de Feynman pour organiser les calculs. Ces diagrammes décrivent les chemins de particules ponctuelles et leurs interactions[11]. Bien que ce formalisme soit très pratique pour faire des prévisions physiques, celles-ci ne sont possibles que lorsque la force des interactions, la constante de couplage, est suffisamment faible pour décrire la théorie comme quasiment sans interactions[30].

L'idée de départ de la théorie des cordes est que les particules ponctuelles peuvent également être modélisées comme des objets unidimensionnels appelés des cordes. L'interaction de cordes est définie en généralisant la théorie des perturbations. Au niveau des diagrammes de Feynman, cela conduit à remplacer le chemin unidimensionnel d'une particule ponctuelle par une surface bidimensionnelle représentant le mouvement d'une corde. À la différence de la théorie quantique des champs, la théorie des cordes ne possède pas de définition non-perturbative complète, et de nombreuses questions théoriques restent hors de portée des physiciens[31].

Ce problème est l'une des motivations originelles pour étudier la correspondance AdS/CFT[22] : elle fournit plusieurs exemples de théories quantiques des champs équivalentes à une théorie des cordes sur un espace anti de Sitter[16].

Paradoxe de l'information[modifier | modifier le code]

Article détaillé : Paradoxe de l'information.

En 1975, Stephen Hawking publie un résultat qui suggère que les trous noirs émettent un faible rayonnement du fait d'effets quantiques près de l'horizon[32]. Ce résultat pose au début un problème théorique car il supposerait que les trous noirs détruisent l'information. Plus précisément, le résultat de Hawking entre en conflit avec l'un des postulats de base de la mécanique quantique, qui stipule que les systèmes physiques évoluent dans le temps selon l'équation de Schrödinger, une propriété généralement mentionnée comme unitarité de l'évolution temporelle. Cette apparente contradiction est par la suite connue comme paradoxe de l'information[33].

La correspondance AdS/CFT résout ce paradoxe, au moins jusqu'à un certain point, car elle montre qu'un trou noir évolue d'une façon cohérente avec la mécanique quantique dans certains contextes. Il est possible de considérer un trou noir dans le contexte de la correspondance AdS/CFT, où il correspond à une configuration de particules sur la frontière d'un espace anti de Sitter[34]. Ces particules obéissent aux règles usuelles de la mécanique quantique et en particulier évoluent unitairement, conduisant le trou noir à évoluer également unitairement, respectant les principes de la mécanique quantique[35]. En 2005, Hawking annonce que le paradoxe est résolu par la correspondance AdS/CFT en faveur de la conservation de l'information et il suggère un mécanisme concret permettant aux trous noirs de la préserver[36].

Applications à la théorie quantique des champs[modifier | modifier le code]

Physique nucléaire[modifier | modifier le code]

Le plasma quark-gluon, un état de la matière exotique produit dans les accélérateurs de particules, a été étudié à l'aide de la correspondance AdS/CFT. Cet état apparaît un bref instant quand des ions lourds tels que des noyaux d'or ou de plomb entrent en collision à hautes énergies. Ces collisions provoquent le déconfinement des quarks des noyaux à des températures d'environ 2 × 1012 K, des conditions similaires à celles présentes 10-11 secondes après le Big Bang[37].

La physique du plasma quark-gluon est gouvernée par la chromodynamique quantique, mais cette théorie est mathématiquement insoluble dans ce genre de problèmes (plus précisément, il est impossible d'y appliquer les méthodes de la théorie des perturbations). En 2005, Đàm Thanh Sơn (en) et ses collaborateurs montrent que la correspondance AdS/CFT pourrait être utilisée pour comprendre certains aspects du plasma quark-gluon plasma en le décrivant dans le langage de la théorie des cordes[25],[26], en termes de trous noirs dans un espace à 5 dimensions. Leurs calculs montrent que le rapport de la viscosité η et de la densité volumique d'entropie s du plasma est approximativement égal à la constante ħ/(4πk) (où ħ est la constante de Planck réduite et k est la constante de Boltzmann)[38],[26]. En 2008, la valeur prédite est confirmée au collisionneur d'ions lourds relativistes du laboratoire national de Brookhaven[25],[39].

Les quarks à très haute énergie se déplaçant dans un plasma quark-gluon plasma sont stoppés après seulement quelques femtomètres. Ce phénomène est caractérisé par le paramètre d'étouffement de jet (en), reliant la perte d'énergie d'un quark au carré de la distance parcourue dans le plasma. Des calculs basés sur la correspondance AdS/CFT ont permis de l'estimer et les résultats sont grossièrement en accord avec sa valeur mesurée expérimentalement[38].

Physique de la matière condensée[modifier | modifier le code]

Un aimant permanent lévitant au-dessus d'un supraconducteur à haute température. Certains physiciens espèrent comprendre ce type de supraconductivité à l'aide de la correspondance AdS/CFT[40].

La physique de la matière condensée expérimentale a découvert un certain nombre d'états exotiques de la matière, dont la supraconductivité et la superfluidité. Ces états sont décrits à l'aide du formalisme de la théorie quantique des champs, mais certains phénomènes sont difficiles à expliquer à l'aide des techniques théoriques standards. Certains physiciens, dont Subir Sachdev (en), espèrent que la correspondance AdS/CFT permettra de décrire ces systèmes à l'aide de la théorie des cordes afin de mieux appréhender leur comportement[25].

Les méthodes de la théorie des cordes ont permis de décrire la transition d'un superfluide à un isolant. Un superfluide est un système d'atomes électriquement neutres qui s'écoule sans frottement. Ces systèmes sont souvent produits en laboratoire à l'aide d'hélium liquide, mais des expériences récentes ont développé de nouvelles manières de productions en déversant des milliards d'atomes froids dans un réseau de lasers entrecroisés. Ces atomes se comportent initialement comme un superfluide, mais en augmentant l'intensité des lasers, ils deviennent moins mobiles et passent soudainement à un état isolant. Pendant la transition, les atomes se comportent de façon inattendue. Par exemple, ils ralentissent et s'arrêtent à une vitesse qui dépend de la température et de la constante de Planck, ce qui ne cadre pas dans la description des autres phases. Ce comportement a été compris en considérant la description duale où les propriétés du fluide sont décrites en termes d'un trou noir de plus hautes dimensions[41].

Critiques[modifier | modifier le code]

Certains théoriciens en physique nucléaire et de la matière condensée ont exprimé leurs doutes quant à la pertinence de la correspondance AdS/CFT pour obtenir les outils permettant de modéliser des systèmes réels de façon réaliste. Lors d'une intervention à la Quark Matter conference en 2006[42], Larry McLerran pointe que la théorie super Yang-Mills N=4 qui apparaît dans la correspondance AdS/CFT diffère significativement de la chromodynamique quantique, la rendant difficile à appliquer à la physique nucléaire. Selon McLerran : « N=4 supersymmetrique Yang-Mills n'est pas la QCD... Elle n'a pas d'échelle de masse et est conformellement invariante. Elle n'a pas de confinement et pas de constante de couplage. Elle est supersymétrique. Elle n'a pas de brisure de symétrie chirale ni de génération de masse. Elle a six particules scalaires et des fermions dans la représentation adjointe... Il est peut-être possible de corriger certains de ces problèmes ou, pour certaines situations physiques, ces objections peuvent ne pas être pertinentes. Actuellement, il n'y a aucun consensus ni arguments convaincants pour les corrections et phénomènes conjecturés qui assureraient que la théorie N=4 supersymétrique Yang Mills reflète la QCD de façon sûre. »[42]

Dans une lettre adressée à Physics Today, le prix Nobel Philip Warren Anderson exprime des inquiétudes similaires à propos des applications d'AdS/CFT à la physique de la matière condensée[43].

Histoire et développement[modifier | modifier le code]

Gerard 't Hooft a obtenu des résultats similaires à la correspondance AdS/CFT dans les années 1970 en étudiant les analogies entre la théorie des cordes et la physique nucléaire.

Théorie des cordes et physique nucléaire[modifier | modifier le code]

Article détaillé : Histoire de la théorie des cordes.

La découverte de la correspondance AdS/CFT en 1997 est l'aboutissement d'une longue série d'efforts pour relier la théorie des cordes et la physique nucléaire[44]. En fait, la théorie des cordes est développée à l'origine à la fin des années 1960 et au début des années 1970 comme une théorie des hadrons, les particules subatomiques tels que le proton et le neutron qui sont maintenus ensemble par l'interaction forte. L'idée était que ces particules pouvaient être vues comme différents modes d'oscillation d'une corde. À la fin des années 1960, les expérimentateurs découvrent que les hadrons suivent des trajectoires de Regge (en) où le carré de l'énergie est proportionnel au moment cinétique, et les théoriciens montrent que cette relation émerge naturellement de la physique d'une corde relativiste en rotation[29].

La tentative de décrire les hadrons comme cordes rencontre toutefois de sérieux problèmes. En particulier, la théorie des cordes inclut une particule de spin 2 sans masse alors qu'aucune particule de ce genre n'apparaît dans la physique des hadrons[44]. Cette particule serait responsable d'une force ayant les propriétés de la gravité. En 1974, Joël Scherk et John Schwarz suggèrent que la théorie des cordes n'est pas une théorie de physique nucléaire, comme de nombreux théoriciens le pensent, mais plutôt une théorie de gravité quantique[45]. À la même époque, on réalise que les hadrons sont en réalité constitués de quarks et l'approche des cordes est abandonnée au bénéfice de la chromodynamique quantique[44].

Dans la chromodynamique quantique, les quarks possèdent une charge de couleur qui peut prendre trois valeurs. En 1974, Gerard 't Hooft étudie la relation entre la théorie des cordes et la physique nucléaire d'un autre point de vue, en considérant des théories similaires à la chromodynamique quantique mais où le nombre de couleurs est un nombre arbitraire N plutôt que 3. Lorsque N tend vers l'infini, 't Hooft affirme que certains calculs de la théorie quantique des champs ressemblent à ceux de la théorie des cordes[46].

Trous noirs et holographie[modifier | modifier le code]

Articles détaillés : Paradoxe de l'information et Principe holographique.
Stephen Hawking prédit en 1975 que les trous noirs émettent un rayonnement par effet quantique.
Leonard Susskind contribue au commencement des idées d'holographie en gravité quantique.

En 1975, Stephen Hawking suggère que les trous noirs émettent un faible rayonnement du fait d'effets quantiques près de l'horizon[32]. Ce résultat prolonge des études de Jacob Bekenstein qui suggèrent que les trous noirs ont une entropie bien définie[47]. Le résultat de Hawking semble entrer initialement en contradiction avec l'un des postulats principaux de la mécanique quantique, à savoir l'unitarité de l'évolution du temps. Intuitivement, ce postulat déclare que les systèmes quantiques ne détruisent pas d'information quand ils évoluent d'un état à un autre. Cette apparente contradiction est appelée paradoxe de l'information[33].

En 1993, Gerard 't Hooft publie un article spéculatif sur la gravité quantique où il revisite le travail de Hawking sur la thermodynamique des trous noirs, concluant que le nombre total de degrés de liberté dans une région de l'espace-temps entourant un trou noir est proportionnel à la superficie de son horizon[48]. Cette idée est soutenue par Leonard Susskind et est connue sous le nom de principe holographique[49]. Ce principe et sa réalisation en théorie des cordes via la correspondance AdS/CFT ont permis d'élucider le mystère des trous noirs et on estime qu'ils fournissent une résolution au paradoxe de l'information[35]. En 2004, Hawking concède que les trous noirs ne violent pas la mécanique quantique[50] et propose un mécanisme concret leur permettant de préserver l'information[36].

Publication de Maldacena[modifier | modifier le code]

Juan Martín Maldacena propose la correspondance AdS/CFT à la fin de l'année 1997.

En 1997, Juan Martín Maldacena publie un article qui marque le début de l'étude de la correspondance AdS/CFT[22]. Selon Alexander Markovich Polyakov, « Le travail [de Maldacena] a ouvert les vannes »[51]. La conjecture suscite immédiatement un grand intérêt dans la communauté de la théorie des cordes[35] et est prise en compte dans des articles de Steven Gubser (en), Igor Klebanov (en) et Polyakov[23], et Edward Witten[24]. Ces articles précisent la conjecture de Maldacena et montrent que la théorie conforme des champs apparaissant dans la correspondance se situe sur la frontière d'un espace anti de Sitter[51].

Un cas spécial de la conjecture de Maldacena déclare que la théorie super Yang-Mills N=4, une théorie de jauge similaire à la chromodynamique quantique, est équivalente à la théorie des cordes dans un espace anti de Sitter de dimension 5[29]. Ce résultat permet de clarifier un travail précédent de 't Hooft sur le lien entre théorie des cordes et chromodynamique quantique[29]. Les résultats de Maldacena fournissent également une réalisation concrète du principe holographique et des implications importantes pour la gravité quantique et la physique des trous noirs[1]. En 2010, l'article Maldacena devient l'article le plus souvent cité en physique des particules avec plus de 7000 citations[3]. Les articles ultérieurs procurent des preuves considérables de l'exactitude de la correspondance, même si elle n'est toujours pas rigoureusement prouvée mathématiquement en 2013[35].

Applications de la correspondance AdS/CFT[modifier | modifier le code]

En 1999, après avoir accepté un emploi à l'Université Columbia, le physicien nucléaire Đàm Thanh Sơn rend visite à Andrei Starinets, un camarade d'université qui effectue un doctorat en théorie des cordes à l'Université de New York[52]. Bien que les deux hommes n'aient pas l'intention de collaborer, Sơn réalise rapidement que les calculs d'AdS/CFT effectués par Starinets pourraient éclairer certains aspects du plasma quark-gluon. En collaboration avec Starinets et Pavel Kovtun, Sơn est capable d'utiliser la correspondance AdS/CFT pour calculer un paramètre clé du plasma[25],[26],[25].

Les physiciens continuent à chercher des applications de la correspondance AdS/CFT en théorie quantique des champs[40],[53]. En plus de ses applications à la physique nucléaire, défendues par Đàm Thanh Sơn et ses collaborateurs, des physiciens de la matière condensée tels que Subir Sachdev utilisent les méthodes de la théorie des cordes pour en comprendre certains aspects. Un résultat notable concerne la transition d'un superfluide en isolant[41]. Un autre sujet émergent est la correspondance fluide/gravité, qui utilise la correspondance AdS/CFT pour traduire des problèmes de la dynamique des fluides en problèmes de relativité générale[54].

Généralisations[modifier | modifier le code]

Gravité tri-dimensionnelle[modifier | modifier le code]

Afin de mieux comprendre les aspects quantiques de la gravité dans notre univers à quatre dimensions, certains physiciens considèrent un modèle mathématique où l'espace-temps n'a que deux dimensions d'espace et une de temps[55]. Dans ce modèle, les mathématiques décrivant le champ gravitationnel sont drastiquement simplifiées et il est possible d'étudier la gravité quantique en utilisant les méthodes familières de la théorie quantique des champs, éliminant le besoin de recourir à la théorie des cordes ou des approches plus radicales (selon Edward Witten, la gravité quantique en trois dimensions peut être comprise en la reliant à la théorie de Chern-Simons[24]).

À partir des travaux de J.D. Brown et Marc Henneaux en 1986[56], les physiciens constatent que la gravité quantique dans un espace-temps tridimensionnel est fortement liée à une théorie conforme des champs bidimensionnelle. En 1995, Henneaux et ses collaborateurs explorent cette relation plus en détail, suggérant que la gravité tridimensionnelle dans un espace anti de Sitter est équivalente à une théorie conforme des champs connue sous le nom de théorie des champs de Liouville[57]. Une autre conjecture formulée par Edward Witten établit que la gravité tridimensionnelle dans un espace anti de Sitter est équivalente à la théorie conforme des champs munie d'une symétrie sur le groupe Monstre[58]. Ces conjectures fournissent des exemples de correspondance AdS/CFT qui ne nécessitent pas l'appareillage de la théorie M ou de la théorie des cordes[59].

Correspondance dS/CFT[modifier | modifier le code]

À la différence de notre univers, que l'on sait désormais en expansion accélérée, un espace anti de Sitter n'est ni en expansion, ni en contraction : il est le même tout le temps[15]. En langage plus technique, un espace anti de Sitter correspond à un univers muni d'une constante cosmologique négative, tandis que l'univers réel possède une constante cosmologique légèrement positive[60].

Bien que les propriétés de la gravité sur de faibles distances soient plutôt indépendantes d'une valeur de la constante cosmologique[61], il est souhaitable d'en obtenir une version de la correspondance AdS/CFT pour une valeur positive. En 2001, Andrew Strominger introduit une version de la dualité appelée correspondance dS/CFT (en)[62]. Cette dualité implique un modèle d'espace-temps appelé espace de Sitter avec une constante cosmologique positive. Une telle dualité est intéressante du point de vue de la cosmologie car de nombreux cosmologistes pensent que l'univers à ses tout débuts était proche d'un espace de Sitter[15]. Il pourrait également ressembler à un espace de Sitter dans un futur lointain[15].

Correspondance Kerr/CFT[modifier | modifier le code]

Bien que la correspondance AdS/CFT soit souvent utile pour étudier les propriétés des trous noirs, la plupart des trous noirs considérés dans son contexte sont physiquement irréalistes. Souvent, la correspondance AdS/CFT met en jeu des modèles d'espace-temps supersymétriques avec trop de dimensions.

En 2009, Monica Guica, Thomas Hartman, Wei Song et Andrew Strominger montrent que les idées d'AdS/CFT peuvent néanmoins être utilisées pour comprendre certains trous noirs astrophysiques. Plus précisément, leurs résultats s'appliquent aux trous noirs approximés par un trou noir de Kerr extrémal, qui a le plus grand moment angulaire possible pour une masse donnée[63]. Ils montrent que de tels trous noirs ont une description équivalente en théorie conforme des champs. La correspondance Kerr/CFT est par la suite étendue aux trous noirs de faible moment angulaire[64].

Théorie de jauge de spin élevé[modifier | modifier le code]

La correspondance AdS/CFT est étroitement liée à une autre dualité conjecturée par Igor Klebanov et Alexander Markovich Polyakov en 2002[65]. Elle déclare que certaines théories de jauge de spin élevé sur un espace anti de Sitter sont équivalentes aux théories conformes des champs avec une symétrie O(N). Ici, la théorie est un type de théorie de jauge décrivant des particules possédant un spin arbitrairement élevé. Elle est similaire à la théorie des cordes, où les modes d'excitation des cordes vibrantes correspondent à des particules de spin élevé, et elle pourrait aider à mieux comprendre les versions d'AdS/CFT concernant la théorie des cordes, voire de prouver la correspondance[66]. En 2010, Simone Giombi et Xi Yin obtiennent des preuves supplémentaires de cette dualité[67].

Annexes[modifier | modifier le code]

Bibliographie[modifier | modifier le code]


Notes et références[modifier | modifier le code]

  1. ↑ a et b de Haro 2013, p. 2.
  2. ↑ Klebanov et Maldacena 2009.
  3. ↑ a et b (en) « Top Cited Articles during 2010 in hep-th », Inspire
  4. ↑ Maldacena 2005, p. 58.
  5. ↑ Griffiths 2004.
  6. ↑ a et b Maldacena 2005, p. 62.
  7. ↑ Wald 1984, p. 4.
  8. ↑ Zwiebach 2009, p. 8.
  9. ↑ Zwiebach 2009, p. 7–8.
  10. ↑ Greene 2000, p. 186.
  11. ↑ a et b Peskin et Schroeder 1995.
  12. ↑ Zee 2010.
  13. ↑ Deligne 1999, p. Volume II.
  14. ↑ Klebanov et Maldacena 2009, p. 28.
  15. ↑ a b c d e et f Maldacena 2005, p. 60.
  16. ↑ a b et c Maldacena 2005, p. 61.
  17. ↑ Fefferman et Graham 1985.
  18. ↑ Fefferman et Graham 2011.
  19. ↑ Zwiebach 2009, p. 552.
  20. ↑ Maldacena 2005, p. 61–62.
  21. ↑ Maldacena 2005, p. 57.
  22. ↑ a b c et d Maldacena 1998.
  23. ↑ a et b Gubser, Klebanov et Polyakov 1998.
  24. ↑ a b et c Witten 1998.
  25. ↑ a b c d e et f Merali 2011, p. 303.
  26. ↑ a b c et d Kovtun, Son et Starinets 2001.
  27. ↑ a et b Moore 2012.
  28. ↑ Alday, Gaiotto et Tachikawa 2010.
  29. ↑ a b c d et e Aharony 2008.
  30. ↑ Zee 2010, p. 43.
  31. ↑ Zwiebach 2009, p. 12.
  32. ↑ a et b Hawking 1975.
  33. ↑ a et b Susskind 2008.
  34. ↑ Zwiebach 2009, p. 554.
  35. ↑ a b c et d Maldacena 2005, p. 63.
  36. ↑ a et b Hawking 2005.
  37. ↑ Zwiebach 2009, p. 559.
  38. ↑ a et b Zwiebach 2009, p. 561.
  39. ↑ Luzum et Romatschke 2008.
  40. ↑ a et b Merali 2011.
  41. ↑ a et b Sachdev 2013, p. 51.
  42. ↑ a et b McLerran 2007.
  43. ↑ (en) Philip Anderson, « Strange connections to strange metals », Physics Today,
  44. ↑ a b et c Zwiebach 2009, p. 525.
  45. ↑ Scherk et Schwarz 1974.
  46. ↑ 't Hooft 1974.
  47. ↑ Bekenstein 1973.
  48. ↑ 't Hooft 1993.
  49. ↑ Susskind 1995.
  50. ↑ Susskind 2008, p. 444.
  51. ↑ a et b Polyakov 2008, p. 6.
  52. ↑ Merali 2011, p. 302–303.
  53. ↑ Sachdev 2013.
  54. ↑ Rangamani 2009.
  55. ↑ Carlip 2003.
  56. ↑ Brown et Henneaux 1986.
  57. ↑ Coussaert, Henneaux et van Driel 1995.
  58. ↑ Witten 2007.
  59. ↑ Guica 2009, p. 1.
  60. ↑ Perlmutter 2003.
  61. ↑ Biquard 2005, p. 33.
  62. ↑ Strominger 2001.
  63. ↑ Guica 2009.
  64. ↑ Castro, Maloney et Strominger 2010.
  65. ↑ Klebanov et Polyakov 2002.
  66. ↑ Klebanov et Polyakov 2002, p. Introduction.
  67. ↑ Giombi et Yin 2010.

Articles connexes[modifier | modifier le code]


v · m
Objets de base
Théories perturbatives
Théories non perturbatives
Autres concepts
Transitions géométriques
Phénoménologie
Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Correspondance_AdS/CFT&oldid=213272464 ».