Coordonnées sphériques

On appelle coordonnées sphériques divers systèmes de coordonnées orthogonales de l'espace analogues aux coordonnées polaires du plan. Un point de l'espace est repéré dans ces systèmes par la distance à une origine (le pôle) et par deux angles. Ils sont d'emploi courant pour le repérage géographique : l'altitude, la latitude et la longitude sont une variante de ces coordonnées. Plusieurs systèmes de coordonnées sphériques sont également employés en astrométrie.
Il existe différentes conventions concernant la définition des angles. Cet article utilise partout (sauf mention explicite contraire) la convention P(ρ,θ,φ), la plus fréquente en particulier en physique et en technologie, où ρ désigne la distance radiale, θ la colatitude (comprise entre 0 et π radians) et φ la longitude (comprise entre 0 et 2π radians).
Histoire[modifier | modifier le code]
Les besoins des astronomes grecs les amenèrent à développer la trigonométrie ; Ménélaos d'Alexandrie en particulier découvrit les principales relations de la trigonométrie sphérique. Des systèmes de coordonnées célestes permettant de repérer la position des étoiles et d'en établir des catalogues remontent à Timocharis d'Alexandrie, Ératosthène et Hipparque, utilisant les mêmes angles (déclinaison et ascension droite en particulier) que les astronomes actuels, bien qu'ils ne les aient pas définis précisément ; en fait, René Descartes est le premier auteur à avoir fourni une description mathématique de systèmes de coordonnées, mais en se limitant au cas des coordonnées cartésiennes. Il semble qu'Alexis Clairaut ait été le premier à définir rigoureusement un système de coordonnées sphériques, dans le cadre de ses travaux de géodésie ; Euler en a développé systématiquement les propriétés, ainsi que leur relation avec les angles qui portent son nom.
Définitions et propriétés élémentaires[modifier | modifier le code]
Conventions[modifier | modifier le code]
Définitions des termes[modifier | modifier le code]
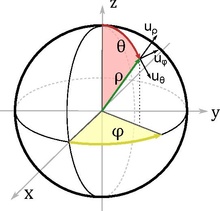
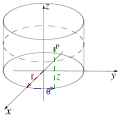
Étant donné un repère cartésien orthonormé (O, x, y, z), les coordonnées sphériques d'un point P (distinct de O, pour lequel longitude et latitude ne sont pas définis, et des points de l'axe Oz, qui n'ont pas de longitude) sont définies par :
- le rayon, le plus souvent noté ρ (mais parfois r) ; c’est la distance du point P au centre O et donc ρ > 0 (ou ρ = 0 pour le point O) ;
- la longitude ; c’est l'angle orienté formé par les demi-plans ayant pour frontière l'axe vertical et contenant respectivement la demi-droite [O, x) et le point P. Si on note H le projeté orthogonal de P dans le plan (O, x, y), la longitude est l'angle formé par les vecteurs x et OH ;
- la colatitude (ou angle zénithal) ; c’est l'angle non orienté formé par les vecteurs z et OP ;
- on utilise parfois la latitude ; c’est l’angle complémentaire de la colatitude, et donc (sauf pour les points de l’axe Oz) l’angle orienté formé par les vecteurs OH et OP.
La colatitude et la longitude seront désignées désormais respectivement par les lettres θ et φ (mais on verra plus bas que ces lettres sont parfois interverties). La latitude est le plus souvent notée δ.
En mathématiques et en physique, les angles sont le plus souvent mesurés en radians, mais dans les applications pratiques, en particulier en géographie et en astronomie, ils sont mesurés en degrés. Par convention, et pour assurer l'unicité des coordonnées, la longitude est comprise entre 0 et 2π radians (0° et 360° ; ou parfois, en géographie en particulier, entre -180° et 180°) et la colatitude est comprise entre 0 et π radians (0° et 180°)[1]. Cette convention vaut pour le repérage mais θ et φ peuvent parcourir un intervalle plus important pour une courbe paramétrée (ρ(t),θ(t),φ(t)), et le rayon peut alors être négatif ; on trouvera plus de précisions dans la section consacrée à la description mathématique de ces systèmes.
Convention rayon-colatitude-longitude[modifier | modifier le code]
Cette convention (revenant à écrire P(ρ,θ,φ), où θ désigne la colatitude et φ la longitude) est la plus utilisée en pratique, et est celle définie par la norme ISO/CEI 80000-2[2]. La distance au centre est parfois notée r[1].
La relation de passage aux coordonnées cartésiennes s'écrit :
Inversement, connaissant les coordonnées cartésiennes, on a :
(cette dernière formule n’étant valable que pour x positif ; dans le cas général, on peut utiliser la fonction atan2(y,x))
Convention rayon-longitude-colatitude[modifier | modifier le code]
En mathématiques, la convention précédente est le plus souvent inversée, désignant la colatitude et la longitude, mais on écrit toujours P(ρ,θ,φ).
La relation de passage aux coordonnées cartésiennes s'écrit dans ce cas :
Convention rayon-longitude-latitude[modifier | modifier le code]

Les mathématiciens emploient parfois ce système, dérivé des conventions utilisées par les géographes. On nomme les coordonnées où :
- désigne la distance du point au centre du repère ;
- désigne la longitude, mesurée depuis l'axe des généralement entre –180° et 180° () ;
- désigne la latitude, l'angle depuis le plan équatorial, entre –90° et 90° ().
L'échange entre les coordonnées cartésiennes et les coordonnées sphériques se fait alors par les formules :
Il est aisé de passer d'un système à un autre car latitude et colatitude sont liées par :
- (ou, en radians, )
Lien avec les coordonnées polaires[modifier | modifier le code]
Dans le plan vertical (O, z, OP), le système de coordonnées (ρ, θ) est polaire. Dans le plan horizontal (O, x, y), (ρsinθ,φ) est aussi un système de coordonnées polaires. En effet, soit , on a , et si H est le projeté de P sur le plan xOy, et ; les coordonnées sphériques du point P vérifient bien :
Relation avec les autres systèmes de coordonnées usuels[modifier | modifier le code]
-
Coordonnées cartésiennes (x,y,z)
-
Coordonnées cylindriques (r,θ,z)
-
Coordonnées sphériques (ρ,θ,φ)
Les coordonnées cartésiennes (x, y, z), cylindriques (r, θ, z) et sphériques (ρ, θ, φ), lorsqu'elles sont définies par rapport au même repère cartésien (O, x, y, z), sont reliées par les formules données ci-dessous.
| Système de coordonnées | Depuis les coordonnées sphériques | Vers les coordonnées sphériques |
|---|---|---|
| Coordonnées cartésiennes | ||
| Coordonnées cylindriques |
Dans le tableau ci-dessus atan2(y, x) est le prolongement classique sur les différents quadrants de arctan(y/x) pour x et y positifs.
Utilisation[modifier | modifier le code]
Un certain nombre de problèmes possèdent des symétries ; l'utilisation de coordonnées sphériques avec certaines symétries peut simplifier grandement l'expression du problème et sa résolution.
Par ailleurs, de nombreuses données peuvent se représenter par des points sur une sphère. Il est donc important d'avoir un système de coordonnées permettant :
- de relever la position d'un point (mesure) ;
- de décrire la position d'un point (résultat d'un calcul par exemple) ;
- d'effectuer une analyse statistique sur une population de points.
De telles données sont appelées données sphériques. Il peut s'agir de position sur un objet sphéroïdal, comme des emplacements sur le globe terrestre. Mais un point sur une sphère peut aussi représenter une direction — le rayon de la sphère n'a alors pas d'importance, et l'on peut se ramener à une sphère de rayon unité.
Repérage géographique[modifier | modifier le code]
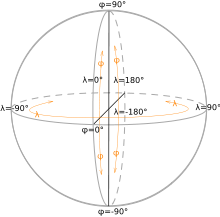
Les coordonnées géographiques, utilisées pour se repérer sur la surface de la Terre, sont une variante des coordonnées sphériques. Elles utilisent comme repère cartésien l'origine au centre de la Terre, l’axe Oz passant par le pôle Nord, l’axe Ox dans le demi-plan du méridien de Greenwich, et l’axe Oy à l’Est de l’axe Ox. Les coordonnées utilisées sont h (altitude), l (latitude) et λ (longitude), qui sont reliées aux coordonnées sphériques (mesurées en degrés) par :
où ρg(l, λ) est la distance au centre de la Terre du point du géoïde situé dans la direction (l, λ). Lorsque l'ellipsoïde de révolution est utilisé à la place du géoïde, h est alors la hauteur géodésique ou hauteur ellipsoïdale, encore nommée hauteur au-dessus de l'ellipsoïde; elle diffère de l'altitude d'environ +/-100 m au plus. La hauteur ellipsoïdale est une grandeur purement géométrique, l'altitude est une grandeur physique. La grandeur h est la distance mesurée le long de la normale à l'ellipsoïde entre ce dernier et le point considéré.
Coordonnées célestes[modifier | modifier le code]
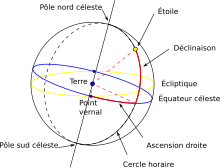
Les coordonnées célestes, utilisées pour repérer les astres sur le ciel, utilisent cette même variante avec ρ fixé (projection sur la sphère céleste). Par exemple, le système de coordonnées équatoriales, servant à repérer les objets hors du système solaire, utilise la déclinaison (correspondant à l, exprimée en degrés) et l'ascension droite (correspondant à λ, exprimée en heures, avec 1 h = 15°).
Calculs[modifier | modifier le code]
Les coordonnées sphériques sont d'emploi courant dans trois cas :
- mouvement à distance fixe d'un point donné, comme dans le cas d'un pendule ;
- mouvement à force centrale, notamment dans le potentiel de Coulomb ;
- problèmes présentant une symétrie sphérique.
Exemple du pendule[modifier | modifier le code]
Exemple de l'attraction coulombienne[modifier | modifier le code]
Données sphériques[modifier | modifier le code]
Les données sphériques sont des relevés de directions d'une droite dans l'espace, exprimées en coordonnées sphériques (avec ρ=1). Si cette droite est orientée, on parle de vecteur unitaire (puisque l'on suppose une sphère de rayon unité), ou simplement vecteur ; si elle n'est pas orientée, on parle d'axe. Un vecteur est un rayon de la sphère unité et peut être représenté par un point P de la sphère. Un axe est un diamètre de la sphère et peut être représenté par un des deux points diamétralement opposés, P ou Q.
Exemples de données[3] :
- vectorielles :
- astrophysique : directions d'arrivée de rayonnements cosmiques,
- géologie structurale : normales à la surface en différents points d'un pli conique ou cylindrique,
- paléomagnétisme : rémanence magnétique dans des roches,
- météorologie : direction des vents à un emplacement donné,
- océanographie physique : mesure des directions des courants marins ;
- axiales :
- cristallographie : orientation d'un cristallite (voir Texture (minéralogie)), direction des axes optiques d'un cristal de quartz dans un galet de quartzite,
- astronomie : normale au plan de l'orbite d'une comète,
- physiologie animale : orientation des champs dendritiques sur la rétine d'un œil de chat.
Calculs de distances[modifier | modifier le code]

Dans des applications pratiques telles que la navigation, on est souvent amené à calculer des distances entre points donnés par leurs coordonnées sphériques (à r constant), ces distances étant mesurées sur la sphère (on dit que ce sont des distances orthodromiques). Pour deux points A et B, on définit donc , où est l'angle (en radians) entre les deux rayons OA et OB. La « formule des cosinus » , donnant une relation entre côtés et angles du triangle sphérique représenté à droite, permet d'en déduire connaissant les coordonnées sphériques A(r, θ, φ) et B(r, θ', φ') ; en plaçant C en (r,0,0), on obtient finalement[4] :
Coordonnées curvilignes[modifier | modifier le code]

Les coordonnées sphériques sont un cas particulier de système de coordonnées curvilignes, et plus précisément de coordonnées orthogonales ; il s'agit d'un repérage par trois nombres, tel que les lignes obtenues en ne faisant varier qu'une coordonnée se coupent à angles droits.
D'un point de vue plus mathématique, cela correspond à une surjection différentiable de dans lui-même, dont la matrice jacobienne est formée de vecteurs colonnes orthogonaux ; pour la convention rayon-colatitude-longitude, cette surjection est définie par : . En pratique (par exemple en astrométrie), on est souvent amené à déterminer au contraire les coordonnées sphériques d'un point de l'espace , autrement dit un antécédent de ce point par ; il n'est pas possible d'obtenir ainsi une application partout continue (c'est le problème de l'holonomie), mais il y a unicité si on choisit pour antécédent (pour tous les points non sur l'axe ) l'unique système tel que (dans certaines applications, par exemple en géographie, on préfère utiliser la latitude, ainsi que la convention ) ; les points de l'axe ont conventionnellement pour coordonnées avec et , et l'origine a pour coordonnées ; cette application (on parle parfois de coordonnées principales) est continue en dehors du demi-plan .
Ce système définit en particulier des lignes de coordonnées (correspondant aux points pour lesquelles deux des trois coordonnées sont fixes) sur la sphère ; ce sont des cercles, les méridiens () et les parallèles (), qui sont orthogonaux deux à deux.
Propriétés différentielles[modifier | modifier le code]
Les formules de changement de repère, correspondant au passage en coordonnées sphériques (dans le système rayon-colatitude-longitude) sont :
d’où la matrice jacobienne[1] : On construit à partir de ces formules un nouveau repère , dit repère local, pour lequel les vecteurs , et sont colinéaires aux vecteurs colonnes de la matrice M et forment un repère orthonormal ; on démontre qu’ils sont respectivement porté par OP, tangent au méridien passant par P, et tangent au parallèle passant par P , ces lignes de coordonnées se coupent donc bien à angle droit, comme expliqué dans la section précédente.
Différentielles[modifier | modifier le code]
Le volume infinitésimal s'écrit :
d3 V = det M dρ dθ dφ= ρ2 sin θ dρ dθ dφ. Ainsi, l'intégrale triple sur tout l'espace de la fonction s'écrira :
- L'élément de surface pour ρ constant s'écrit
d2 Sρ = ρ2 sin θ dθ dφ
- On en déduit l'élément d'angle solide (en stéradians) :
- L'élément de surface pour φ constant s'écrit
d2 Sφ = ρ dρ dθ
- L'élément de surface pour θ constant s'écrit
d2 Sθ = ρ sin θ dρ dφ
Les vecteurs ont pour différentielles[1] :
Cinématique[modifier | modifier le code]
Les calculs de ce paragraphe correspondent à l'étude cinématique d'une courbe paramétrée par le temps t : .
On déduit des différentielles précédentes les dérivées par rapport au temps :
puis les quantités cinématiques vitesse et accélération :
Opérateurs différentiels[modifier | modifier le code]
L'opérateur nabla s'écrit
On en déduit les expressions du gradient, du rotationnel, de la divergence et du laplacien[1] :
Tenseurs usuels[modifier | modifier le code]
Le tenseur métrique s'écrit[1]
Les éléments non nuls du symbole de Christoffel sont[1]
Généralisation en dimension n[modifier | modifier le code]
Dans l'espace euclidien de dimension n, pour un point de coordonnées cartésiennes (x1, …, xn), on définit les coordonnées hypersphériques (r, θ1, …, θn–1) par[5]
avec
Les coordonnées sphériques constituent le cas particulier n = 3 (avec un choix convenable de numérotation des axes) et les coordonnées polaires le cas n = 2 ; on pourra consulter la section correspondante de l'article 3-sphère pour le cas n = 4.
Notes et références[modifier | modifier le code]
- (en) Eric W. Weisstein, « Spherical Coordinates », sur MathWorld.
- « Signes et symboles mathématiques à utiliser en sciences physiques et en technologie » : ISO 80000-2 (1ère ed., 1/12/2009) (p.24) [PDF].
- (en) N. I. Fisher, T. Lewis et B. J. J. Lembleton, Statistical Analysis of Spherical Data, Cambridge University Press, , 329 p. (ISBN 978-0-521-24273-8, lire en ligne), p. 1.
- Comment obtenir la distance entre deux points connus en longitude et latitude sur la sphère sur le site géodésie.ign.fr
- (en) Luis Manuel Braga de Costa Campos, Generalized Calculus with Applications to Matter and ForcesMathematics and Physics for Science and Technology, CRC Press, (lire en ligne), p. 686-687.





















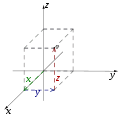








































![{\displaystyle {\begin{aligned}{\overrightarrow {\mathrm {grad} }}~f={\overrightarrow {\nabla }}f={}&{\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}},\\[8pt]{\overrightarrow {\operatorname {rot} }}\ {\vec {\mathrm {A} }}={\overrightarrow {\nabla }}\wedge {\vec {\mathrm {A} }}={}&{\frac {1}{r\sin \theta }}\left({\partial \over \partial \theta }\left(A_{\varphi }\sin \theta \right)-{\partial A_{\theta } \over \partial \varphi }\right){\hat {\mathbf {r} }}\\[8pt]&{}+{\frac {1}{r}}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}\left(rA_{\varphi }\right)\right){\hat {\boldsymbol {\theta }}}\\[8pt]&{}+{\frac {1}{r}}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\hat {\boldsymbol {\varphi }}},\\[8pt]{\mathrm {div} }~{\vec {\mathrm {A} }}={\overrightarrow {\nabla }}\cdot {\vec {\mathrm {A} }}={}&{\frac {1}{r^{2}}}{\partial \over \partial r}\left(r^{2}A_{r}\right)+{\frac {1}{r\sin \theta }}{\partial \over \partial \theta }\left(\sin \theta A_{\theta }\right)+{\frac {1}{r\sin \theta }}{\partial A_{\varphi } \over \partial \varphi },\\[8pt]\Delta f={\overrightarrow {\nabla }}^{2}f={}&{1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}\\[8pt]={}&\left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}\right)f+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)f+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}f.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78dd97cf11515224cdcaf3438ca7226cbfce19f3)



![{\displaystyle \theta _{1},\ldots ,\theta _{n-2}\in [0,\pi ]\quad {\rm {et}}\quad \theta _{n-1}\in [0,2\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48c08d56aa4a0d22f613ef068dc8e6a9271239e6)