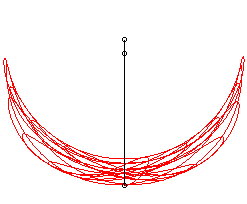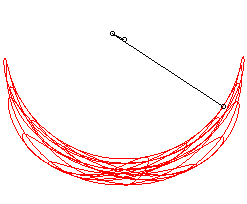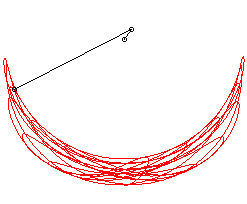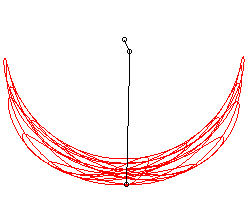
Illustration de la sensibilité aux conditions initiales avec trois pendules doubles aux conditions de départ très proches. En mécanique , on désigne par pendule double un pendule à l'extrémité duquel on accroche un autre pendule. Son évolution est généralement chaotique .
Un pendule double est un système dynamique typiquement limité à un mouvement plan . Il comporte deux degrés de libertés (
θ
1
,
θ
2
{\displaystyle \theta _{1},\,\theta _{2}}
l
1
,
l
2
,
m
1
,
m
2
,
g
{\displaystyle l_{1},\,l_{2},\,m_{1},\,m_{2},\,g}
Le pendule est constitué de deux tiges de longueur
l
1
{\displaystyle l_{1}\,}
l
2
{\displaystyle l_{2}\,}
m
1
{\displaystyle m_{1}\,}
m
2
{\displaystyle m_{2}\,}
L'énergie cinétique vaut :
T
=
1
2
m
1
v
1
2
+
1
2
m
2
v
2
2
=
1
2
m
1
l
1
2
θ
˙
1
2
+
1
2
m
2
[
l
1
2
θ
˙
1
2
+
l
2
2
θ
˙
2
2
+
2
l
1
l
2
θ
˙
1
θ
˙
2
cos
(
θ
1
−
θ
2
)
]
{\displaystyle T={\frac {1}{2}}m_{1}v_{1}^{2}+{\frac {1}{2}}m_{2}v_{2}^{2}={\frac {1}{2}}m_{1}l_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}[l_{1}^{2}{\dot {\theta }}_{1}^{2}+l_{2}^{2}{\dot {\theta }}_{2}^{2}+2l_{1}l_{2}{\dot {\theta }}_{1}{\dot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})]}
θ
i
{\displaystyle \theta _{i}\,}
v
i
{\displaystyle v_{i}\,}
i
{\displaystyle i\,}
V
=
m
1
g
z
1
+
m
2
g
z
2
{\displaystyle V=m_{1}gz_{1}+m_{2}gz_{2}\,}
z
i
{\displaystyle z_{i}\,}
i
{\displaystyle i\,}
V
=
−
(
m
1
+
m
2
)
g
l
1
cos
(
θ
1
)
−
m
2
g
l
2
cos
(
θ
2
)
{\displaystyle V=-(m_{1}+m_{2})gl_{1}\cos(\theta _{1})-m_{2}gl_{2}\cos(\theta _{2})\,}
lagrangien vaut donc :
L
=
T
−
V
{\displaystyle L=T-V\,}
L
=
1
2
(
m
1
+
m
2
)
l
1
2
θ
˙
1
2
+
1
2
m
2
l
2
2
θ
˙
2
2
+
m
2
l
1
l
2
θ
˙
1
θ
˙
2
cos
(
θ
1
−
θ
2
)
+
(
m
1
+
m
2
)
g
l
1
cos
(
θ
1
)
+
m
2
g
l
2
cos
(
θ
2
)
{\displaystyle L={\frac {1}{2}}(m_{1}+m_{2})l_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}l_{2}^{2}{\dot {\theta }}_{2}^{2}+m_{2}l_{1}l_{2}{\dot {\theta }}_{1}{\dot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+(m_{1}+m_{2})gl_{1}\cos(\theta _{1})+m_{2}gl_{2}\cos(\theta _{2})}
En appliquant les équations de Lagrange , on obtient les équations du mouvement :
(
m
1
+
m
2
)
l
1
θ
¨
1
+
m
2
l
2
θ
¨
2
cos
(
θ
1
−
θ
2
)
+
m
2
l
2
θ
˙
2
2
sin
(
θ
1
−
θ
2
)
+
(
m
1
+
m
2
)
g
sin
(
θ
1
)
=
0
l
1
θ
¨
1
cos
(
θ
1
−
θ
2
)
+
l
2
θ
¨
2
−
l
1
θ
˙
1
2
sin
(
θ
1
−
θ
2
)
+
g
sin
(
θ
2
)
=
0
{\displaystyle {\begin{array}{l}(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})=0\\l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})=0\end{array}}}
Dans le cas particulier
m
1
=
m
2
,
l
1
=
l
2
{\displaystyle m_{1}=m_{2},\,l_{1}=l_{2}}
système d'unités idoine, ces équations deviennent :
2
θ
¨
1
+
θ
¨
2
cos
(
θ
1
−
θ
2
)
+
θ
˙
2
2
sin
(
θ
1
−
θ
2
)
+
2
sin
(
θ
1
)
=
0
θ
¨
2
+
θ
¨
1
cos
(
θ
1
−
θ
2
)
+
sin
(
θ
2
)
=
θ
˙
1
2
sin
(
θ
1
−
θ
2
)
{\displaystyle {\begin{array}{l}2{\ddot {\theta }}_{1}+{\ddot {\theta }}_{2}\cos \left(\theta _{1}-\theta _{2}\right)+{\dot {\theta }}_{2}^{2}\sin \left(\theta _{1}-\theta _{2}\right)+2\sin \left(\theta _{1}\right)=0\\{\ddot {\theta }}_{2}+{\ddot {\theta }}_{1}\cos \left(\theta _{1}-\theta _{2}\right)+\sin \left(\theta _{2}\right)={\dot {\theta }}_{1}^{2}\sin \left(\theta _{1}-\theta _{2}\right)\\\end{array}}}
Aucune solution explicite n'étant connue, la résolution passe typiquement par l'utilisation de méthodes numériques .
Autour du minimum énergétique (voir section suivante), ce système possède des solutions périodiques décomposables en deux modes, mais il est chaotique , c’est-à-dire qu'il possède aussi des solutions ni périodiques ni pseudo-périodiques , mais présentant en permanence un mouvement original, et qu'il est alors sensible aux conditions initiales .
Le système est à l'équilibre pour
θ
1
=
θ
2
=
θ
˙
1
=
θ
˙
2
=
0
{\displaystyle \theta _{1}=\theta _{2}={\dot {\theta }}_{1}={\dot {\theta }}_{2}=0}
approximations de MacLaurin
sin
θ
=
θ
{\displaystyle \sin \theta =\theta }
cos
θ
=
1
{\displaystyle \cos \theta =1}
système linéaire :
(
m
1
+
m
2
)
l
1
θ
¨
1
+
m
2
l
2
θ
¨
2
+
(
m
1
+
m
2
)
g
θ
1
=
0
l
1
θ
¨
1
+
l
2
θ
¨
2
+
g
θ
2
=
0
{\displaystyle {\begin{alignedat}{5}(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}&&\;+\;&&m_{2}l_{2}{\ddot {\theta }}_{2}&&\;+\;&&(m_{1}+m_{2})g\theta _{1}&&\;=\;&&0&\\l_{1}{\ddot {\theta }}_{1}&&\;+\;&&l_{2}{\ddot {\theta }}_{2}&&\;+\;&&g\theta _{2}&&\;=\;&&0&\end{alignedat}}}
Le double pendule peut alors être analysé en termes de modes normaux , en remarquant que le système ci-dessus peut être réduit à la forme matricielle
M
θ
→
¨
+
K
θ
→
=
0
→
{\displaystyle M{\ddot {\vec {\theta }}}+K{\vec {\theta }}={\vec {0}}}
Par exemple, pour
m
1
=
m
2
{\displaystyle m_{1}=m_{2}}
l
1
=
l
2
=
l
{\displaystyle l_{1}=l_{2}=l}
[
θ
¨
1
θ
¨
2
]
=
g
l
[
−
2
1
2
−
2
]
[
θ
1
θ
2
]
{\displaystyle {\begin{bmatrix}{\ddot {\theta }}_{1}\\{\ddot {\theta }}_{2}\end{bmatrix}}={\frac {g}{l}}{\begin{bmatrix}-2&1\\2&-2\end{bmatrix}}{\begin{bmatrix}\theta _{1}\\\theta _{2}\end{bmatrix}}}
Les équations du mouvement peuvent également être trouvées en utilisant les complexes.
Représentons le double pendule ci-dessus dans le plan complexe de Gauss, en posant que l’axe des réels a même sens et même direction que la gravitation. Les points m1 et m2 représentant les mobiles 1 et 2 correspondent aux affixes z1 et z2 . En fait, seuls les angles vont varier en fonction du temps puisque la masse et la longueur sont des constantes. Il faut donc chercher une manière de représenter les fonctions
θ
1
{\displaystyle \theta _{1}}
θ
2
{\displaystyle \theta _{2}}
Dès lors, puisque le module de z1 vaut l1 , son argument
θ
1
{\displaystyle \theta _{1}}
z
1
=
l
1
(
cos
θ
1
+
i
sin
θ
1
)
=
l
1
e
i
θ
1
{\displaystyle z_{1}=l_{1}(\cos \theta _{1}+i\sin \theta _{1})=l_{1}e^{i\theta _{1}}}
2 est issu d’une translation de z1 par le complexe z0 =
l
2
e
i
θ
2
{\displaystyle l_{2}e^{i\theta _{2}}}
2 et son argument
θ
2
{\displaystyle \theta _{2}}
2 = z1 + z0 , donc
z
2
=
l
1
e
i
θ
1
+
l
2
e
i
θ
2
{\displaystyle z_{2}=l_{1}e^{i\theta _{1}}+l_{2}e^{i\theta _{2}}}
Ici, les complexes z1 et z2 déterminent la position des mobiles1 et 2 en fonction du temps puisque
θ
1
(
t
)
{\displaystyle \theta _{1}(t)}
θ
2
(
t
)
{\displaystyle \theta _{2}(t)}
1 vaut
a
z
1
=
d
2
z
1
d
t
2
=
l
1
(
i
θ
¨
1
−
θ
˙
1
2
)
e
i
θ
1
{\displaystyle a_{z_{1}}={\operatorname {d^{2}} \!z_{1} \over \operatorname {d} \!t^{2}}=l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})e^{i\theta _{1}}}
et que celle de la deuxième est égale à
a
z
2
=
d
2
z
2
d
t
2
=
l
1
(
i
θ
¨
1
−
θ
˙
1
2
)
e
i
θ
1
+
l
2
(
i
θ
¨
2
−
θ
˙
2
2
)
e
i
θ
2
{\displaystyle a_{z_{2}}={\operatorname {d^{2}} \!z_{2} \over \operatorname {d} \!t^{2}}=l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})e^{i\theta _{1}}+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})e^{i\theta _{2}}}
Notons-les respectivement
z
¨
1
{\displaystyle {\ddot {z}}_{1}}
z
¨
2
{\displaystyle {\ddot {z}}_{2}}
Revenons dans la vie réelle. Quand une masse est suspendue à une corde, une tension se produit le long de celle-ci. Appelons, T1 et T2 , les tensions exercées par les masses m1 et m2 et représentons-les sous forme de complexes t1 et t2 .
Nous observons alors que t1 , z1 et 0 sont alignés ou colinéaires, ce qui permet d’écrire que
t
1
=
k
1
z
1
(
k
1
∈
R
)
{\displaystyle t_{1}=k_{1}z_{1}\,(k_{1}\in \mathbb {R} )}
2 , z0 et 0 sont alignés, ce qui permet d’affirmer que
t
2
=
k
2
z
0
(
k
2
∈
R
)
{\displaystyle t_{2}=k_{2}z_{0}\,(k_{2}\in \mathbb {R} )}
La formule de la dynamique F = m a , connue aussi sous le nom de la 2e loi de Newton, dit que la somme de toutes les forces appliquées à un mobile est égale au produit de l’accélération de celui-ci par sa masse.
Le mobile 2 est soumis à la tension T2 et la force due à la gravité m2 g, donnant les relations suivantes :
F
=
m
a
z
2
=
t
2
+
m
2
g
⟺
m
2
z
¨
2
−
m
2
g
=
t
2
⟺
z
¨
2
−
g
=
t
2
m
2
=
k
2
z
0
m
2
⇒
z
¨
2
−
g
z
0
=
k
2
m
2
.
.
.
(
1
)
{\displaystyle F=ma_{z_{2}}=t_{2}+m_{2}g\Longleftrightarrow m_{2}{\ddot {z}}_{2}-m_{2}g=t_{2}\Longleftrightarrow {\ddot {z}}_{2}-g={\frac {t_{2}}{m_{2}}}={\frac {k_{2}z_{0}}{m_{2}}}\,\Rightarrow \,{\frac {{\ddot {z}}_{2}-g}{z_{0}}}={\frac {k_{2}}{m_{2}}}\,...(1)}
Le mobile 1 est soumis à la tension T1 , à la force due à la gravité m1 g et à la tension T2 ’ qui est issue du principe des actions réciproques (la 3e loi de Newton) telle que T2 ’= - T2 . Dès lors, nous pouvons dire que
F
=
m
a
z
1
=
t
1
−
t
2
+
m
1
g
⟺
t
1
=
t
2
−
m
1
g
+
m
1
z
¨
1
⟺
t
1
=
m
2
z
¨
2
−
m
2
g
−
m
1
g
+
m
1
z
¨
1
{\displaystyle F=ma_{z_{1}}=t_{1}-t_{2}+m_{1}g\Longleftrightarrow t_{1}=t_{2}-m_{1}g+m_{1}{\ddot {z}}_{1}\Longleftrightarrow t_{1}=m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}
⟺
m
2
z
¨
2
−
m
2
g
−
m
1
g
+
m
1
z
¨
1
=
k
1
z
1
⟺
m
2
z
¨
2
−
m
2
g
−
m
1
g
+
m
1
z
¨
1
z
1
=
k
1
.
.
.
(
2
)
{\displaystyle \Longleftrightarrow m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}=k_{1}z_{1}\Longleftrightarrow {\frac {m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}{z_{1}}}=k_{1}\,...(2)}
Les membres de droite des équations (1) et (2) étant réels, exprimons que la partie imaginaire des membres de gauche est nulle :
Tout d’abord, concernant l’équation (1).
Calculons le membre de gauche.
z
¨
2
−
g
z
0
=
l
1
(
i
θ
¨
1
−
θ
˙
1
2
)
e
i
θ
1
+
l
2
(
i
θ
¨
2
−
θ
˙
2
2
)
e
i
θ
2
−
g
l
2
e
i
θ
2
{\displaystyle {\frac {{\ddot {z}}_{2}-g}{z_{0}}}={\frac {l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})e^{i\theta _{1}}+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})e^{i\theta _{2}}-g}{l_{2}e^{i\theta _{2}}}}}
=
l
1
i
θ
¨
1
cos
θ
1
−
l
1
θ
˙
1
2
cos
θ
1
−
l
1
θ
¨
1
sin
θ
1
−
l
1
i
θ
˙
1
2
sin
θ
1
+
l
2
i
θ
¨
2
cos
θ
2
−
l
2
θ
˙
2
2
cos
θ
2
−
l
2
θ
¨
2
sin
θ
2
−
l
2
i
θ
˙
2
2
sin
θ
2
−
g
l
2
cos
θ
2
+
l
2
i
sin
θ
2
{\displaystyle ={\frac {l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2}-g}{l_{2}\cos \theta _{2}+l_{2}i\sin \theta _{2}}}}
Appliquons le binôme conjugué pour supprimer le terme imaginaire au dénominateur, ce qui revient à multiplier la fraction par
cos
θ
2
−
i
sin
θ
2
cos
θ
2
−
i
sin
θ
2
{\displaystyle {\frac {\cos \theta _{2}-i\sin \theta _{2}}{\cos \theta _{2}-i\sin \theta _{2}}}}
Maintenant, seuls les imaginaires purs intéressent. C’est pourquoi, relevons uniquement les imaginaires purs issus du produit du numérateur par le conjugué du dénominateur. Nous conservons alors uniquement :
(
l
1
i
θ
¨
1
cos
θ
1
−
l
1
i
θ
˙
1
2
sin
θ
1
+
l
2
i
θ
¨
2
cos
θ
2
−
l
2
i
θ
˙
2
2
sin
θ
2
)
(
cos
θ
2
)
{\displaystyle (l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2})(\cos \theta _{2})}
+
(
−
l
1
θ
˙
1
2
cos
θ
1
−
l
1
θ
¨
1
sin
θ
1
−
l
2
θ
˙
2
2
cos
θ
2
−
l
2
θ
¨
2
sin
θ
2
−
g
)
(
−
i
sin
θ
2
)
{\displaystyle +(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-g)(-i\sin \theta _{2})}
Ainsi, nous pouvons affirmer que :
Im
(
z
¨
2
−
g
z
0
)
{\displaystyle {\text{Im}}({\frac {{\ddot {z}}_{2}-g}{z_{0}}})}
=
l
1
θ
¨
1
cos
θ
1
cos
θ
2
−
l
1
θ
˙
1
2
sin
θ
1
cos
θ
2
+
l
2
θ
¨
2
cos
2
θ
2
−
l
2
θ
˙
2
2
cos
θ
2
sin
θ
2
l
2
{\displaystyle ={\frac {l_{1}{\ddot {\theta }}_{1}\cos \theta _{1}\cos \theta _{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{2}+l_{2}{\ddot {\theta }}_{2}\cos ^{2}\theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}\sin \theta _{2}}{l_{2}}}}
+
l
1
θ
˙
1
2
sin
θ
2
cos
θ
1
+
l
1
θ
¨
1
sin
θ
1
sin
θ
2
+
l
2
θ
˙
2
2
sin
θ
2
cos
θ
2
+
l
2
θ
¨
2
sin
2
θ
2
+
g
sin
θ
2
l
2
{\displaystyle +{\frac {l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{2}\cos \theta _{1}+l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}\sin \theta _{2}+l_{2}{\dot {\theta }}_{2}^{2}\sin \theta _{2}\cos \theta _{2}+l_{2}{\ddot {\theta }}_{2}\sin ^{2}\theta _{2}+g\sin \theta _{2}}{l_{2}}}}
=
l
1
θ
¨
1
cos
(
θ
1
−
θ
2
)
+
l
2
θ
¨
2
−
l
1
θ
˙
1
2
sin
(
θ
1
−
θ
2
)
+
g
sin
(
θ
2
)
l
2
{\displaystyle ={\frac {l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})}{l_{2}}}}
Comme il faut que la partie imaginaire soit nulle, nous obtenons cette première équation différentielle.
l
1
θ
¨
1
cos
(
θ
1
−
θ
2
)
+
l
2
θ
¨
2
−
l
1
θ
˙
1
2
sin
(
θ
1
−
θ
2
)
+
g
sin
(
θ
2
)
=
0
{\displaystyle l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})=0}
Ensuite, concernant l’équation (2). Nous procédons de la même manière. Calculons le membre de gauche.
m
2
z
¨
2
−
m
2
g
−
m
1
g
+
m
1
z
¨
1
z
1
{\displaystyle {\frac {m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}{z_{1}}}}
=
m
2
[
l
1
(
i
θ
¨
1
−
θ
˙
1
2
)
(
cos
θ
1
+
i
sin
θ
1
)
+
l
2
(
i
θ
¨
2
−
θ
˙
2
2
)
(
cos
θ
2
+
i
sin
θ
2
)
]
−
m
2
g
−
m
1
g
+
m
1
[
l
1
(
i
θ
¨
1
−
θ
˙
1
2
)
(
cos
θ
1
+
i
sin
θ
1
)
]
l
1
cos
θ
1
+
l
1
i
sin
θ
1
{\displaystyle ={\frac {m_{2}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})(\cos \theta _{2}+i\sin \theta _{2})]-m_{2}g-m_{1}g+m_{1}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}
=
m
1
[
l
1
i
θ
¨
1
cos
θ
1
−
l
1
θ
˙
1
2
cos
θ
1
−
l
1
θ
¨
1
sin
θ
1
−
l
1
i
θ
˙
1
2
sin
θ
1
]
−
m
1
g
−
m
2
g
l
1
cos
θ
1
+
l
1
i
sin
θ
1
{\displaystyle ={\frac {m_{1}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}]-m_{1}g-m_{2}g}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}
+
m
2
[
l
1
i
θ
¨
1
cos
θ
1
−
l
1
θ
˙
1
2
cos
θ
1
−
l
1
θ
¨
1
sin
θ
1
−
l
1
i
θ
˙
1
2
sin
θ
1
+
l
2
i
θ
¨
2
cos
θ
2
−
l
2
θ
˙
2
2
cos
θ
2
−
l
2
θ
¨
2
sin
θ
2
−
l
2
i
θ
˙
2
2
sin
θ
2
]
l
1
cos
θ
1
+
l
1
i
sin
θ
1
{\displaystyle +{\frac {m_{2}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2}]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}
Appliquons le binôme conjugué pour supprimer le terme imaginaire au dénominateur, ce qui revient à multiplier la fraction par
cos
θ
1
−
i
sin
θ
1
cos
θ
1
−
i
sin
θ
1
{\displaystyle {\frac {\cos \theta _{1}-i\sin \theta _{1}}{\cos \theta _{1}-i\sin \theta _{1}}}}
Maintenant, seuls les imaginaires purs intéressent. C’est pourquoi, relevons uniquement les imaginaires purs issus du produit du numérateur par le conjugué du dénominateur. Nous gardons alors uniquement
[
m
1
(
l
1
i
θ
¨
1
cos
θ
1
−
l
1
i
θ
˙
1
2
sin
θ
1
)
+
m
2
(
l
1
i
θ
¨
1
cos
θ
1
−
l
1
i
θ
˙
1
2
sin
θ
1
+
l
2
i
θ
¨
2
cos
θ
2
−
l
2
i
θ
˙
2
2
sin
θ
2
)
]
[
cos
θ
1
]
{\displaystyle [m_{1}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1})+m_{2}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2})][\cos \theta _{1}]}
+
[
m
1
(
−
l
1
θ
˙
1
2
cos
θ
1
−
l
1
θ
¨
1
sin
θ
1
)
+
m
2
(
−
l
1
θ
˙
1
2
cos
θ
1
−
l
1
θ
¨
1
sin
θ
1
−
l
2
θ
˙
2
2
cos
θ
2
−
l
2
θ
¨
2
sin
θ
2
)
−
m
1
g
−
m
2
g
]
[
−
i
sin
θ
1
]
{\displaystyle +[m_{1}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1})+m_{2}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2})-m_{1}g-m_{2}g][-i\sin \theta _{1}]}
Ainsi, nous pouvons affirmer que
Im
(
m
2
z
¨
2
−
m
2
g
−
m
1
g
+
m
1
z
¨
1
z
1
)
{\displaystyle {\text{Im}}({\frac {m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}{z_{1}}})}
=
m
1
l
1
θ
¨
1
cos
2
θ
1
−
m
1
l
1
θ
˙
1
2
sin
θ
1
cos
θ
1
+
m
2
l
1
θ
¨
1
cos
2
θ
1
−
m
2
l
1
θ
˙
1
2
sin
θ
1
cos
θ
1
+
m
2
l
2
θ
¨
2
cos
θ
1
cos
θ
2
l
1
{\displaystyle ={\frac {m_{1}l_{1}{\ddot {\theta }}_{1}\cos ^{2}\theta _{1}-m_{1}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{2}l_{1}{\ddot {\theta }}_{1}\cos ^{2}\theta _{1}-m_{2}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos \theta _{1}\cos \theta _{2}}{l_{1}}}}
+
−
m
2
l
2
θ
˙
2
2
sin
θ
2
cos
θ
1
+
m
1
l
1
θ
˙
1
2
sin
θ
1
cos
θ
1
+
m
1
l
1
θ
¨
1
sin
2
θ
1
+
m
2
l
1
θ
˙
1
2
sin
θ
1
cos
θ
1
+
m
2
l
1
θ
¨
1
sin
2
θ
1
l
1
{\displaystyle +{\frac {-m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin \theta _{2}\cos \theta _{1}+m_{1}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{1}l_{1}{\ddot {\theta }}_{1}\sin ^{2}\theta _{1}+m_{2}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{2}l_{1}{\ddot {\theta }}_{1}\sin ^{2}\theta _{1}}{l_{1}}}}
+
m
2
l
2
θ
˙
2
2
sin
θ
1
cos
θ
2
+
m
2
l
2
θ
¨
2
sin
θ
1
sin
θ
2
+
m
1
sin
θ
1
g
+
m
2
sin
θ
1
g
l
1
{\displaystyle +{\frac {m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin \theta _{1}\cos \theta _{2}+m_{2}l_{2}{\ddot {\theta }}_{2}\sin \theta _{1}\sin \theta _{2}+m_{1}\sin \theta _{1}g+m_{2}\sin \theta _{1}g}{l_{1}}}}
=
(
m
1
+
m
2
)
l
1
θ
¨
1
+
m
2
l
2
θ
¨
2
cos
(
θ
1
−
θ
2
)
+
m
2
l
2
θ
˙
2
2
sin
(
θ
1
−
θ
2
)
+
(
m
1
+
m
2
)
g
sin
(
θ
1
)
l
1
{\displaystyle ={\frac {(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})}{l_{1}}}}
Comme il faut que la partie imaginaire soit nulle, nous obtenons cette deuxième différentielle.
(
m
1
+
m
2
)
l
1
θ
¨
1
+
m
2
l
2
θ
¨
2
cos
(
θ
1
−
θ
2
)
+
m
2
l
2
θ
˙
2
2
sin
(
θ
1
−
θ
2
)
+
(
m
1
+
m
2
)
g
sin
(
θ
1
)
=
0
{\displaystyle (m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})=0}
Nous avons donc pour finir :
{
l
1
θ
¨
1
cos
(
θ
1
−
θ
2
)
+
l
2
θ
¨
2
−
l
1
θ
˙
1
2
sin
(
θ
1
−
θ
2
)
+
g
sin
(
θ
2
)
=
0
(
m
1
+
m
2
)
l
1
θ
¨
1
+
m
2
l
2
θ
¨
2
cos
(
θ
1
−
θ
2
)
+
m
2
l
2
θ
˙
2
2
sin
(
θ
1
−
θ
2
)
+
(
m
1
+
m
2
)
g
sin
(
θ
1
)
=
0
{\displaystyle {\begin{cases}l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})=0\\(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})=0\end{cases}}}
Ce sont les mêmes équations que pour l'approche lagrangienne.
Un autre exercice classique concerne le cas où la première tige se meut d'un mouvement uniforme autour de son axe. On a alors
θ
1
˙
=
ω
{\displaystyle {\dot {\theta _{1}}}=\omega }
θ
2
=
θ
{\displaystyle \theta _{2}=\theta \,}
l
2
θ
¨
=
−
l
1
ω
2
sin
(
θ
−
ω
t
)
−
g
sin
θ
=
−
(
1
+
l
1
ω
2
g
cos
ω
t
)
g
sin
θ
+
l
1
ω
2
sin
ω
t
cos
θ
{\displaystyle l_{2}{\ddot {\theta }}=-l_{1}\omega ^{2}\sin(\theta -\omega t)-g\sin \theta =-(1+{\frac {l_{1}\omega ^{2}}{g}}\cos \omega t)g\sin \theta +l_{1}\omega ^{2}\sin \omega t\cos \theta }
Pour de petites oscillations et
l
1
ω
2
g
<<
1
{\displaystyle {\frac {l_{1}\omega ^{2}}{g}}<<1\,}
l
2
θ
¨
+
g
θ
=
l
1
ω
2
sin
(
ω
t
)
{\displaystyle l_{2}{\ddot {\theta }}+g\theta =l_{1}\omega ^{2}\sin(\omega t)}
oscillateur harmonique forcé :
Mais si, dans ce cas, on choisit
ω
=
g
/
l
2
{\displaystyle \omega ={\sqrt {g/l_{2}}}\,}











![{\displaystyle T={\frac {1}{2}}m_{1}v_{1}^{2}+{\frac {1}{2}}m_{2}v_{2}^{2}={\frac {1}{2}}m_{1}l_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}[l_{1}^{2}{\dot {\theta }}_{1}^{2}+l_{2}^{2}{\dot {\theta }}_{2}^{2}+2l_{1}l_{2}{\dot {\theta }}_{1}{\dot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7073757e61f4d9b036fa221b288a48b440eb2e6c)














































![{\displaystyle ={\frac {m_{2}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})(\cos \theta _{2}+i\sin \theta _{2})]-m_{2}g-m_{1}g+m_{1}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3609a7fee57f3e4bbca35dbbd5bc71ca6e59d931)
![{\displaystyle ={\frac {m_{1}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}]-m_{1}g-m_{2}g}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4931dc3625d298fda933c8825749628282868826)
![{\displaystyle +{\frac {m_{2}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2}]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15fab123eec0b163e6ef3f75238d8ef6b84949be)

![{\displaystyle [m_{1}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1})+m_{2}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2})][\cos \theta _{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499742e18caed9187d9806f4399d367e3ebb832e)
![{\displaystyle +[m_{1}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1})+m_{2}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2})-m_{1}g-m_{2}g][-i\sin \theta _{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/638316eca7e8ce7ddaaea707b6629cc0a3d6afe9)













