Propagation des ondes
En physique ondulatoire, la propagation d'une onde correspond au déplacement spatial de la perturbation du milieu engendrée par une onde. Sa direction est par définition celle du flux d'énergie que transporte l'onde.

La grandeur principale caractérisant la propagation d'une onde est sa vitesse de propagation. Selon la nature de l'onde, on distingue vitesse de groupe et vitesse de phase. En général, la direction de propagation d'une onde et celle du vecteur d'onde coïncident[N 1].
Milieu de propagation[modifier | modifier le code]
Certaines ondes ne peuvent se propager que dans un milieu matériel, comme le son ou les vagues. On les nomme ondes mécaniques.

Certaines ondes ont la propriété de pouvoir se propager même dans le vide, comme la lumière ou les ondes radio. Les ondes électromagnétiques et les ondes gravitationnelles en font partie.
Vitesse de propagation[modifier | modifier le code]
La vitesse de propagation d'une onde correspond à la vitesse de translation de son profil. Pour une onde harmonique monochromatique, elle est liée à sa longueur d'onde λ, à sa fréquence f et à sa période T par les égalités suivantes :
Équation de propagation[modifier | modifier le code]
La propagation d'une onde est régie par l'équation de D'Alembert :
avec l'amplitude de l'onde au point et à l'instant .
En dimension , l'équation des ondes devient :
La dérivée par rapport au temps de est une dérivée seconde, et donc l'onde qui remonte le temps vérifie la même équation. Cette invariance par retournement du temps découle du caractère réversible de la propagation d'une onde.
Modes de propagation[modifier | modifier le code]
En dimension d'espace, on distingue deux modes de propagation : les ondes progressives, qui se déplacent dans la direction de l'axe, et les ondes régressives, qui se déplacent dans la direction opposée. Elles correspondent en fait aux deux familles de solutions générales de l'équation des ondes en dimension .

Les ondes stationnaires sont des ondes qui oscillent mais qui ne se propagent pas. Elles sont pourtant la résultante d'ondes qui se propagent.

Les ondes évanescentes sont également des ondes qui ne se propagent pas. Un exemple serait de bouger l'extrémité d'une corde assez lentement pour que la corde suive le mouvement de l'opérateur sans que l'on aperçoive d'impulsion apparaître.
Phénomènes affectant la propagation des ondes[modifier | modifier le code]
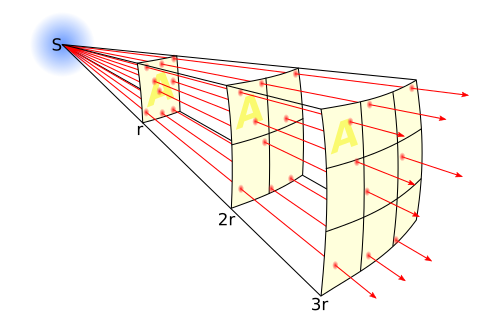
La propagation d'une onde s'accompagne toujours d'un amortissement qui traduit une perte de l'énergie de l'onde, soit parce qu'elle est absorbée par le milieu, soit parce que l'onde se répartit sur une plus grande zone de l'espace ce qui diffuse l'énergie.
On peut aussi citer :
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Un contre-exemple serait la propagation d'une onde électromagnétique dans un matériau anisotrope, possédant un indice qui dépenderait de la direction. Le vecteur de Poynting et le vecteur d'onde ne sont alors pas colinéaires.
Références[modifier | modifier le code]
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Simulations[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
Lev Landau et Evgueni Lifchits, Physique théorique, t. 7 : Théorie de l'élasticité [détail des éditions]









