Conjecture de Goldbach

La conjecture de Goldbach est l'assertion mathématique qui s’énonce comme suit :
Tout nombre entier pair supérieur à 3 peut s’écrire comme la somme de deux nombres premiers.
Formulée en 1742 par Christian Goldbach, c’est l’un des plus vieux problèmes non résolus de la théorie des nombres et des mathématiques. Il partage avec l'hypothèse de Riemann et la conjecture des nombres premiers jumeaux le numéro 8 des problèmes de Hilbert, énoncés par celui-ci en 1900.
La figure ci-contre montre les solutions de l’équation 2N = p + q représentées par des ronds, où 2N est un nombre pair entre 4 et 50, et p et q sont deux nombres premiers : les nombres 2N sont représentés par les lignes horizontales et les nombres premiers p et q sont représentés par les lignes inclinées rouges et bleues. La conjecture de Goldbach correspond au fait qu’aussi loin qu’on prolonge la figure vers le bas, toute ligne horizontale grise contiendra au moins un rond :
| 4 | = | 2 + 2 | (1 solution) | |||
| 6 | = | 3 + 3 | (1 solution) | |||
| 8 | = | 3 + 5 | (1 solution) | |||
| 10 | = | 3 + 7 | = 5 + 5 | (2 solutions) | ||
| 12 | = | 5 + 7 | (1 solution) | |||
| 14 | = | 3 + 11 | = 7 + 7 | (2 solutions) | ||
| 50 | = | 19 + 31 | = 13 + 37 | = 7 + 43 | = 3 + 47 | (4 solutions) |
La conjecture de Goldbach est un cas particulier d’une conjecture liée à l’hypothèse H de Schinzel.
Origine[modifier | modifier le code]

Le , le mathématicien prussien Christian Goldbach écrit au mathématicien suisse Leonhard Euler une lettre à la fin de laquelle il propose la conjecture suivante :
Tout nombre strictement supérieur à 2 peut être écrit comme une somme de trois nombres premiers.
(Goldbach admettait 1 comme nombre premier ; la conjecture moderne exclut 1, et remplace donc[1] 2 par 5.)
Dans sa réponse datée du , Euler rappelle à Goldbach que cet énoncé découle d'un énoncé antérieur[2] que Goldbach lui avait déjà communiqué :
Tout nombre pair peut être écrit comme somme de deux nombres premiers.
(Comme précédemment, « nombre » est à prendre au sens « entier strictement supérieur à 0 » et la conjecture moderne remplace[1] 0 par 2.)
Selon une version plus faible de la conjecture, tout nombre impair supérieur ou égal à 9 est somme de trois nombres premiers.
Justification heuristique[modifier | modifier le code]
La majorité des mathématiciens pense que la conjecture de Goldbach est vraie, en se basant surtout sur des considérations statistiques axées sur la répartition des nombres premiers : plus le nombre est grand, plus il y a de manières disponibles pour le représenter sous forme de somme de deux ou trois autres nombres, et la plus « compatible » devient celle pour laquelle au moins une de ces représentations est constituée entièrement de nombres premiers.
Une version très grossière de l'argument probabiliste heuristique (pour la forme forte de la conjecture de Goldbach) est la suivante. Le théorème des nombres premiers affirme qu'un entier m sélectionné aléatoirement d'une manière brute possède chance d'être premier. Ainsi, si n est un grand entier pair et m, un nombre compris entre 3 et n/2, alors on peut s'attendre à ce que la probabilité que m et n – m soient tous deux premiers soit égale à . Cet argument heuristique n'est pas rigoureux pour de nombreuses raisons ; par exemple, on suppose que les événements que m et n – m soient premiers sont statistiquement indépendants l'un de l'autre. Si l'on poursuit quand même ce raisonnement heuristique, on peut estimer que le nombre total de manières d'écrire un grand nombre entier pair n comme la somme de deux nombres premiers impairs vaut environ
Puisque cette quantité tend vers l'infini lorsque n augmente, on peut s'attendre à ce que tout entier pair suffisamment grand non seulement possède au moins une représentation sous forme de somme de deux nombres premiers, mais en fait en possède beaucoup.
L'argument heuristique ci-dessus est en fait quelque peu imprécis, car il ignore certaines corrélations entre les probabilités que m et n – m soient premiers. Par exemple, si m est impair alors n – m aussi, et si m est pair alors n – m aussi, or les nombres premiers sont tous impairs à part 2. De même, si n est divisible par 3 et si m est déjà un nombre premier distinct de 3, alors n – m est aussi premier avec 3 donc sa probabilité d'être premier est légèrement supérieure à celle d'un entier quelconque. En poursuivant ce type d'analyse avec plus de soin, Hardy et Littlewood conjecturèrent en 1923 (c'est une partie de la célèbre conjecture des n-uplets premiers de Hardy-Littlewood) que pour tout c ≥ 2, le nombre de représentations d'un grand entier n sous la forme de somme de c premiers avec devrait être équivalent à où le produit porte sur tous les nombres premiers p, et est le nombre de solutions de l’équation en arithmétique modulaire, soumise aux contraintes . Cette formule asymptotique a été démontrée pour c ≥ 3 à partir du travail de Vinogradov, mais est encore à l'état de conjecture pour c = 2. Dans ce dernier cas, l'expression ci-dessus est nulle lorsque n est impair, et lorsque n est pair elle se simplifie en où est la constante des nombres premiers jumeaux Cette formule asymptotique est quelquefois appelée conjecture étendue de Goldbach. La conjecture forte de Goldbach est en fait très similaire à celle des nombres premiers jumeaux, et les deux conjectures sont présumées de difficultés comparables.
État des recherches[modifier | modifier le code]
Théorèmes apparentés[modifier | modifier le code]
Dans le cadre de recherches en vue de démontrer la conjecture de Goldbach, plusieurs théoriciens des nombres ont abouti à des théorèmes plus faibles que la conjecture. Le tableau suivant présente quelques étapes significatives de ces recherches. La mention f indique les théorèmes en rapport avec la conjecture faible de Goldbach, « tout nombre impair supérieur ou égal à 9 est somme de trois nombres premiers. » :
| Année | Auteurs | Théorème | Détails | |
|---|---|---|---|---|
| 1920 | Viggo Brun | Tout entier pair assez grand est somme de deux entiers composés chacun de 9 facteurs premiers au plus. | ||
| 1923 | Hardy et Littlewood | f | En supposant vraie une certaine généralisation de l'hypothèse de Riemann, tout nombre impair assez grand est somme de trois nombres premiers[3]. | |
| 1924 | Hans Rademacher | Tout entier pair assez grand est somme de deux entiers composés chacun de 7 facteurs premiers au plus. | ||
| 1931 | Lev Schnirelmann | Tout entier > 1 est somme de 20 nombres premiers au plus. | ||
| 1937 | Ivan Vinogradov | f | Tout entier impair assez grand est somme de trois nombres premiers. Corollaire : Tout entier pair assez grand est somme de quatre nombres premiers. |
|
| 1937 | Nikolai Chudakov (en)[4] | Presque tout entier pair est somme de deux nombres premiers[5]. | ||
| 1938 | Johannes van der Corput[6] | |||
| 1938 | Theodor Estermann[7] | |||
| 1947 | Alfréd Rényi | Il existe une constante K telle que tout entier pair est somme d’un nombre premier et d’un nombre ayant au plus K facteurs premiers. | ||
| 1951 | Yuri Linnik | Il existe une constante K telle que tout entier pair assez grand est somme de deux nombres premiers et d’au plus K puissances de 2. | ||
| 1966 | Chen Jingrun | Tout entier pair assez grand est somme d’un nombre premier et d’un nombre ayant au plus deux facteurs premiers. | ||
| 1975 | Hugh Montgomery et Robert Charles Vaughan |
La plupart des entiers pairs sont la somme de deux nombres premiers[8]. | ||
| 1995 | Olivier Ramaré | Tout entier pair est somme de six nombres premiers au plus. Corollaire : Tout entier impair est somme de sept nombres premiers au plus. |
[lire en ligne][9] | |
| 1997 | Jean-Marc Deshouillers, Gove Effinger, Herman te Riele et Dimitri Zinoviev | f | L'hypothèse de Riemann généralisée implique la conjecture faible de Goldbach. | [lire en ligne][PDF][10] |
| 2002 | Roger Heath-Brown et Jan-Christoph Schlage-Puchta |
Le résultat de Linnik (1951) vaut avec K = 13. | ||
| 2012 | Terence Tao | f | Tout entier impair > 1 est somme de cinq nombres premiers au plus. Corollaire : résultat d’Olivier Ramaré, 1995. |
Article détaillé (preuve en cours de vérification) |
| 2013 | Harald Helfgott | f | Tout entier impair > 5 est somme de trois nombres premiers. Corollaire : résultat de Terence Tao, 2012. |
Article détaillé (preuve en cours de vérification) |
Vérifications numériques[modifier | modifier le code]
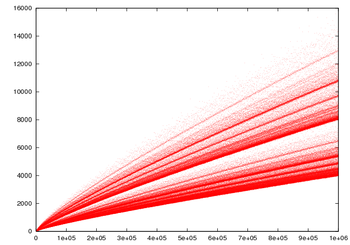
En 2014, les vérifications numériques publiées conduisent aux conclusions suivantes :
- la conjecture de Goldbach est vérifiée pour tous les entiers pairs jusqu’à 4.1018 (Tomás Oliveira e Silva, Siegfried Herzog et Silvio Pardi[11]) ;
- la conjecture faible de Goldbach est vérifiée pour tous les entiers impairs jusqu’à 8,875.1030 (H. A. Helfgott et David J. Platt[12]).
Dans la culture[modifier | modifier le code]
- En 2007, Luis Piedrahita et Rodrigo Sopeña produisent le film espagnol La Cellule de Fermat (La Habitación de Fermat) mettant en scène un jeune mathématicien qui affirme faussement avoir démontré la conjecture et un vieux mathématicien qui, lui, l'aurait démontrée.
- Le roman Oncle Petros et la Conjecture de Goldbach [détail des éditions], d'Apóstolos Doxiádis, raconte l'histoire fictive d'un mathématicien ayant consacré sa vie professionnelle à la seule conjecture de Goldbach, gaspillant ainsi ses ressources intellectuelles et se mettant lui-même à l'écart de la vie scientifique et de sa famille. Le roman en profite surtout pour fournir un éclairage culturel sur quelques mathématiciens et logiciens du début du siècle (Kurt Gödel, Alan Turing, Srinivasa Ramanujan, Godfrey Harold Hardy…) et les rapports entre leurs différents travaux.
- Afin de faire de la publicité pour le livre de Doxiádis, l'éditeur britannique Tony Faber offrit en 2000 un prix d'un million de dollars américains pour une preuve de la conjecture. Le prix ne pouvait être attribué qu'à condition que la preuve soit soumise à publication avant . Il n'a jamais été réclamé.
- Le roman Le Théorème du Perroquet, de Denis Guedj, met en scène un mathématicien qui, au fond de l'Amazonie, réussit à démontrer la conjecture de Goldbach. Refusant de la livrer à l'humanité, il se suicide en brûlant ses recherches. Mais avant, il la fait apprendre par son perroquet. Des mafieux veulent s'approprier l’oiseau mais ce dernier reste muet. Excédés, ils l'abattent. Le roman se termine dans la forêt où le perroquet, blessé, récite la démonstration aux autres animaux. Elle demeure ainsi inconnue des humains.
- Le film Le Théorème de Marguerite (2023) d'Anna Novion présente une normalienne, Marguerite, qui travaille sur la résolution d'un pan de la conjecture de Goldbach[13].
Notes et références[modifier | modifier le code]
- Mais avec ce remplacement, la conjecture moderne est un peu plus forte que l’originale.
- En fait, les deux conjectures sont équivalentes : si tout nombre pair supérieur à 2 peut s'écrire comme somme de trois premiers, l'un d'entre eux est nécessairement 2, et alors tout nombre pair supérieur à 0 peut s'écrire comme somme de deux premiers. Notons qu'Euler présente à Goldbach sa version comme étant celle reçue de lui : « …so Ew. vormals mit mir communicirt haben, dass nehmlich ein jeder numerus par eine summa duorum numerorum primorum sey… », Lettre XLIV.
- Autrement dit : sous l'hypothèse indiquée, la conjecture faible de Goldbach est valable pour tout nombre impair assez grand.
- Nikolai G. Chudakov, « On the Goldbach problem », Doklady Akademii Nauk SSSR, vol. 17, , p. 335-338.
- D’après le travail de Vinogradov, et dans le sens que la proportion des nombres pairs qui peuvent s’écrire sous cette forme tend vers 1.
- (en) J. G. Van der Corput, « Sur l’hypothèse de Goldbach », Proc. Akad. Wet. Amsterdam, vol. 41, , p. 76-80.
- (en) T. Estermann, « On Goldbach’s problem: proof that almost all even positive integers are sums of two primes », Proc. London Math. Soc., vol. 44, , p. 307-314 (DOI 10.1112/plms/s2-44.4.307).
- Plus précisément, il existe deux constantes positives c et C telles que, pour tout nombre N assez grand, tout entier pair inférieur à N est somme de deux nombres premiers, avec au plus exceptions. En particulier, l’ensemble des entiers pairs qui ne sont pas la somme de deux nombres premiers a pour densité zéro.
- (en) O. Ramaré, « On Šnirel'man's constant », Ann. Scuola Norm. Sup. Pisa Cl. Sci., vol. 22, no 4, , p. 645-706 (lire en ligne).
- (en) Deshouillers, Effinger, te Riele et Zinoviev, « A complete Vinogradov 3-primes theorem under the Riemann hypothesis », Electronic Research Announcements of the American Mathematical Society, vol. 3, 1997, p. 99-104.
- (en) Tomás Oliveira e Silva, Siegfried Herzog et Silvio Pardi, « Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4.1018 », Math. Comp., vol. 83, , p. 2033-2060 (DOI 10.1090/S0025-5718-2013-02787-1, lire en ligne).
- (en) H. A. Helfgott et David J. Platt, « Numerical Verification of the Ternary Goldbach Conjecture up to 8.875.1030 », Exper. Math., vol. 22, no 4, , p. 406-409 (DOI 10.1080/10586458.2013.831742, arXiv 1305.3062).
- Odile Morain, « Le Théorème de Marguerite : Jean-Pierre Darroussin et Ella Rumpf dans la folie créatrice des maths », sur Franceinfo, (consulté le )
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Projet de calcul distribué des nombres de Goldbach
- (en) Chris Caldwell, Goldbach’s conjecture, sur le site Prime Pages
- (en) Tomás Oliveira e Silva, « Goldbach conjecture verification »















