Somme (arithmétique)
En mathématiques, la somme de deux nombres est le résultat de leur addition. Les éléments additionnés s’appellent les termes de la somme. Elle se calcule de différentes manières selon le système de numération employé. Du fait de la commutativité et de l'associativité de l'addition, la somme d'un ensemble fini de nombres est bien définie indépendamment de l'ordre dans lequel est faite l'addition, mais il n'existe pas toujours de formule réduite pour l'exprimer. Les méthodes employées pour obtenir de telles formules sont liées à l'étude des séries numériques.
Les sommes de suites de nombres peuvent être notées à l'aide du symbole somme , dont la graphie évoque la lettre grecque sigma capitale.
La limite d'une série est également appelée une somme, même si elle ne s'obtient pas directement par une addition finie.
Notation[modifier | modifier le code]

La notation mathématique utilise un symbole qui représente la somme d'une suite de termes : le symbole de sommation, Σ, une forme élargie de la lettre grecque sigma capitale. Celui-ci est défini comme suit :
où i représente l'indice de sommation ; ai est une variable indexée représentant chaque nombre successif de la série ; m est la limite inférieure de sommation, et n est la limite supérieure de sommation. Le « i = m » sous le symbole de sommation signifie que l'indice i débute avec la valeur m. L'indice, i, est incrémenté de 1 à chaque itération, et s'arrêtant quand i = n[1].
Voici un exemple montrant une somme de carrés :
La notation informelle omet parfois la définition de l'indice et de ses limites de sommation lorsque ceux-ci sont clairs au vu du contexte, comme dans :
On voit souvent des généralisations de cette notation dans lesquelles une condition logique arbitraire est fournie, et la somme est destinée à prendre en charge toutes les valeurs satisfaisant cette condition. Par exemple :
est la somme de sur tous les (entiers) dans un ordre spécifique,
est la somme de sur tous les de l'ensemble (si est l'ensemble vide, la somme est nulle : voir « Somme vide »), et
est la somme de sur tous les entiers positifs divisant .
Il existe aussi des façons de généraliser l'utilisation de plusieurs signes sigma. Par exemple,
signifie
Une notation similaire est appliquée en ce qui concerne le produit d'une suite de nombre qui est similaire à la sommation, mais qui utilise la multiplication au lieu de l'addition (et donne 1 pour une suite vide au lieu de 0). La structure de base utilisée est la même, avec , une forme élargie de la lettre grecque Pi majuscule, remplaçant le .
Définition formelle[modifier | modifier le code]
La somme peut être définie récursivement comme suit
- , pour b < a.
- , pour b ≥ a.
Exemples[modifier | modifier le code]
Somme des premiers entiers[modifier | modifier le code]

Pour tout entier n, la somme des entiers de 1 à n vaut :
Le calcul de cette somme fait l'objet d'une légende[2],[3],[4],[5] concernant Carl Friedrich Gauss, selon laquelle peu après son septième anniversaire[6], il aurait stupéfié son maître d'école Büttner en calculant très rapidement la somme des entiers de 1 à 100, alors que le maître s'attendait à ce que ce calcul occupât toute la classe un long moment. Gauss additionne 1 avec 100, puis 2 avec 99, puis 3 avec 98 et ainsi de suite jusqu'à 50 avec 51. Il obtient une somme de 50 fois la valeur 101, soit 5 050. Seule l'anecdote est peut-être infondée ; la méthode, en revanche, est correcte et s'applique à n'importe quel entier n. On peut la reformuler ainsi :
On a ainsi : d'où l'on tire :
Une autre méthode consiste à vérifier cette formule par récurrence sur n : notons Sn la somme des entiers de 1 à n. La formule Sn = n(n + 1)/2 est vraie pour n = 1[7] et si elle est vraie à l'ordre n – 1 alors elle l'est à l'ordre n car
D'autres démonstrations font appel à l'arithmétique géométrique : voir l'article Nombre triangulaire, § « Méthodes de calcul ».
Somme des premiers entiers impairs[modifier | modifier le code]
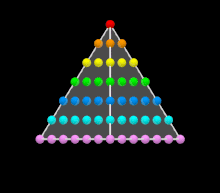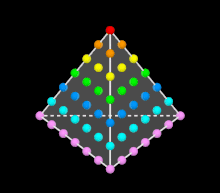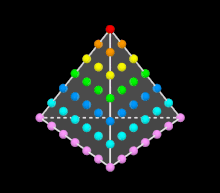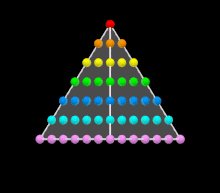
Pour tout entier n supérieur à 1, la somme des n premiers impairs vaut n² :
Exemples :
- 1=1²,
- 1+3=2²,
- 1+3+5=3², etc.
Il s'agit d'un cas particulier de somme de termes d'une suite arithmétique. Ici c'est la suite arithmétique de raison 2 et de premier terme 1 dont on calcule la somme des n premiers termes.
Somme des premières puissances[modifier | modifier le code]
Pour tout entier n, la somme des n premiers carrés d'entiers vérifie l'identité :
Cette identité peut faire l'objet de nombreuses démonstrations différentes. La plus simple consiste en une simple démonstration par récurrence, mais nécessite que la formule soit connue au préalable. Une méthode pour retrouver la formule sans qu'elle soit connue est de considérer le signe somme comme une opération d'intégration, ce qui amène naturellement à chercher une « primitive » de n2 comme un polynôme de degré 3 : P(n) = an³ + bn² + cn + d. Le terme primitive correspond ici à une notion d'intégrale discrète, c'est-à-dire qu'on souhaite que soit vérifiée l'équation :
Cette équation amène aux valeurs , puis en sommant l'identité précédente pour k allant de 0 jusqu'à n, permet de montrer l'identité annoncée.
Une autre méthode, fondée aussi sur cette idée de primitive, consiste à partir de l'identité :
et à la sommer pour k allant de 0 jusqu'à n, ce qui permet d'obtenir :
En supposant déjà connue la formule pour la somme des n premiers entiers, l'identité souhaitée s'en déduit.
Ces deux méthodes par primitive permettent de généraliser au calcul de la somme des n premières puissances p-èmes ; la deuxième nécessitant toutefois un calcul par récurrence sur p. Les formules obtenues pour p = 3 et p = 4 sont :
- ;
- .
Les formules générales, appelées formules de Faulhaber, font intervenir les nombres de Bernoulli.
Diviseurs d'un entier[modifier | modifier le code]
Tout entier strictement positif a un nombre fini de diviseurs, qui peuvent être listés par test successifs sur les entiers strictement inférieurs ou par produits de combinaisons de ses facteurs premiers.
La somme des diviseurs σ définit une fonction arithmétique, c'est-à-dire que si a et b sont deux entiers premiers entre eux, on a σ(ab) = σ(a) σ(b).
L'entier 6 est parfait car il est égal à la somme de ses diviseurs stricts : s(6) = 1+2+3 = 6. L'entier 10 est déficient : s(10) = 1+2+5 = 8 < 10. L'entier 12 est abondant : s(12) = 1+2+3+4+6 = 16 > 12.
Coefficients binomiaux[modifier | modifier le code]
Pour tout n ∈ N, pour tout entier k entre 0 et n, le coefficient binomial correspond au nombre de combinaisons de k éléments dans un ensemble de n éléments.
La somme de ces coefficients pour n fixé, autrement dit la somme des termes sur une ligne du triangle de Pascal, correspond donc au nombre de parties d'un ensemble à n éléments, ce qui donne l'égalité
La somme des coefficients binomiaux selon une diagonale du triangle de Pascal satisfait aussi la formule :
Sommes de Riemann[modifier | modifier le code]
Sous des hypothèses sur les intervalles et la fonction , les sommes de Riemann s'écrivent :
Elles permettent de calculer l'intégrale de la fonction :
Autres sommes[modifier | modifier le code]
Les relations suivantes sont des identités :
- (somme d'une suite arithmétique), d'où
- (La somme des n premiers nombres impairs vaut n², voir animation)

- Pour x ≠ 1, (voir « Série géométrique »).
- (voir « Constante d'Euler-Mascheroni »).
Pour des exemples de sommes infinies, voir « Série (mathématiques) ».
Calcul effectif[modifier | modifier le code]
Si l'associativité et la commutativité de l'addition permettent en théorie de calculer une somme de plusieurs termes dans n'importe quel ordre, en pratique les approximations successives peuvent mener à des résultats différents en fonction de l'ordre choisi.
>>> sum(1/n**4 for n in range(1, 100001)) 1.082323233710861 >>> sum(1/n**4 for n in range(100000, 0, -1)) 1.082323233711138 |
Notes et références[modifier | modifier le code]
- Pour un exposé détaillé sur la notation de la sommation, et l'arithmétique avec sommes, voir (en) Ronald L. Graham, Donald E. Knuth et Oren Patashnik, Concrete Mathematics : A Foundation for Computer Science, Addison-Wesley, , 2e éd. (ISBN 978-0-201-55802-9, lire en ligne), chap. 2 (« Sums »).
- Brian Hayes (en) a recensé 111 versions différentes de cette légende, toutes aussi romancées (voir son article « Gauss's Day of Reckoning » dans American Scientist, vol. 94, n° 3, mai-juin 2006 DOI 10.1511/2006.3.200).
- L'origine de l'information remonte à l'essai biographique sur Gauss écrit par Wolfgang Sartorius von Waltershausen, Gauss zum Gedächtnis, 1856, p. 12-13 ; les nombres de 1 à 100 ne sont pas indiqués, ni la méthode pour y parvenir.
- « Si non è vero, è bene trovato », sur UJF Grenoble, .
- Thérèse Eveilleau, « L'escalier des entiers », sur Mathématiques magiques, présente une version de plus de cette anecdote et des exemples d'application de cette méthode.
- Wolfgang Sartorius von Waltershausen, Gauss zum Gedächtnis, 1856, p. 12-13
- Et même pour n = 0, avec la convention que la somme vide S0 est nulle.












































