Conductivité thermique
| Unités SI | Watt par mètre-kelvin (W m−1 K−1) |
|---|---|
| Dimension | M·L·T −3·Θ −1 |
| Nature | Grandeur scalaire intensive |
| Symbole usuel | ou |
| Lien à d'autres grandeurs | = |
La conductivité thermique (ou conductibilité thermique) d'un matériau est une grandeur physique qui caractérise sa capacité à diffuser la chaleur dans les milieux sans déplacement macroscopique de matière[1]. C'est le rapport de l'énergie thermique (quantité de chaleur) transférée par unité de temps (donc homogène à une puissance, en watts) et de surface au gradient de température. Notée λ (anciennement K voire k), la conductivité thermique intervient notamment dans la loi de Fourier.
Généralités[modifier | modifier le code]
Quand le matériau considéré est homogène et isotrope, la loi de Fourier s'écrit[1] :
où :
- désigne la densité de flux thermique (W/m2),
- λ la conductivité thermique (W m−1 K−1),
- l'opérateur gradient,
- T la température (K).
Un matériau a par exemple une conductivité thermique de 1 W m−1 K−1 si un gradient thermique de 1 K/m induit par conduction un flux thermique de 1 W/m2 (de sens opposé au gradient).
Lorsque le matériau est anisotrope, sa conductivité thermique varie selon les directions. Le λ mentionné dans la loi de Fourier peut alors s'exprimer par un tenseur de conductivité[2] :
- λ =
avec les remarques suivantes :
- > 0
- =
Définir les axes de coordonnées selon des directions particulières permet de simplifier le tenseur de conductivité en annulant tous les coefficients de la matrice qui ne sont pas des coefficients diagonaux. Le λ de la loi de Fourier s'exprime alors de la manière suivante[2] :
- λ =
Considérons une paroi d'épaisseur e dont les deux surfaces externes, planes et d'aire S, sont maintenues à des températures uniformes et constantes T1 et T2 (avec par exemple ). Alors la puissance thermique Φ transférée à travers la paroi est [1] :
Dans le système international d'unités Φ s'exprime en watts (W).
La conductivité thermique du matériau d'une paroi (mesurée en laboratoire et indiquée dans la documentation des fabricants) et son épaisseur permettent notamment de calculer les déperditions thermiques au travers de cette paroi sur une période déterminée (un an, un hiver, etc.).
Exemple : une paroi d'un mètre carré de surface et d'un mètre d'épaisseur, de conductivité thermique 0,5 W m−1 K−1, est soumise à un flux de chaleur de 0,5 W pour une différence de température de 1 K entre ses deux faces, soit en une heure une déperdition de 0,5 Wh.
Plus la conductivité thermique est élevée, plus le matériau est conducteur de chaleur ; plus elle est faible, plus il est isolant. Le cuivre, avec une conductivité thermique de 380 W m−1 K−1, est ainsi plus de 10 000 fois plus conducteur de la chaleur que le polyuréthane (0,023 W m−1 K−1)[3].
La conductivité dépend principalement de :
- la nature du matériau ;
- la température ;
- d’autres paramètres comme l’humidité et la pression.
La conductivité thermique va généralement de pair avec la conductivité électrique. Les métaux par exemple, bons conducteurs de l'électricité, sont aussi de bons conducteurs thermiques. Il y a des exceptions, comme le diamant qui a une conductivité thermique élevée (entre 1 000 et 2 600 W m−1 K−1) alors que sa conductivité électrique est basse, tandis que le graphène (5 300 W m−1 K−1) est meilleur conducteur thermique et bien meilleur conducteur électrique (du moins dans certaines directions, car c'est un matériau fortement anisotrope).
Conductivité des gaz[modifier | modifier le code]
La conductivité des gaz purs et des mélanges peut être calculée à partir de la méthode de Chapman-Enskog en utilisant un potentiel d'interaction molécule-molécule tel que le potentiel Lennard-Jones. Cette propriété de transport macroscopique (domaine continu) est l'image des transferts de quantité de mouvement et d'énergie à l'échelle moléculaire qui croissent avec la force des collisions, donc avec la température et qui s'opposent à l'advection de la quantité de mouvement dans le milieu.
Corps purs[modifier | modifier le code]
La conductivité d'un corps pur sans degré de liberté interne est étroitement liée à sa viscosité et donnée par l'expression suivante
où est la température, la masse molaire, le nombre d'Avogadro, la constante de Boltzmann, la section efficace et l'intégrale de collision réduite par sa valeur utilisant un potentiel sphères dures. Ce terme dépend faiblement de la température, il est donc voisin de l'unité. Si on prend on retrouve l'approximation d'un milieu composé de sphères dures parfaitement élastiques. Le terme représente le nombre de collisions par unité de temps.
La chaleur massique à volume constant est réduite à sa composante liée à la translation :
La contribution des degrés de liberté internes est obtenue en utilisant la corrélation d'Eucken.
La quantité est souvent disponible dans les bases de données sous forme tabulée[4] ou sous forme polynomiale
où peut être négatif. On trouve également des approximations faisant intervenir des termes en .
Ce type d'approximation est également utilisé pour donner une expression numérique [5].
Mélanges gazeux[modifier | modifier le code]


La conductivité translationnelle d'un mélange gazeux de corps est solution d'un système algébrique linéaire d'ordre et de rang [4],[6]. Elle s'exprime donc sous la forme où est la fraction volumique de l'espèce dans le mélange. Il existe nombre d'approximations précises dans un domaine plus ou moins large (voir figure ci-contre). Elles sont généralement basées sur une approximation de la solution formelle sous forme d'une série de déterminants. On obtient ainsi[7] :
avec (par exemple) :
Où est le coefficient de diffusion binaire.
Beaucoup d'autres approximations sont possibles[7],[8].
On peut obtenir avec le même type de méthode des approximations de la conductivité interne, avec cependant une précision assez modeste (voir courbes).
Conductivité des solides[modifier | modifier le code]
À l'échelle atomique, le transfert de chaleur dans les solides peut être réalisé par le biais de toute particule ou quasi-particule. La conductivité thermique correspond à la somme des contributions de celles-ci. Dans les solides, le transfert de chaleur est principalement dû aux phonons, aux électrons et aux magnons. Les magnons peuvent représenter une part importante de la conductivité thermique dans certains matériaux comme les cuprates. Des contributions d'autres particules restent possibles[9].
Dans les métaux, le mouvement des électrons libres est prépondérant dans la conduction de chaleur du fait de leur vitesse importante, bien qu'une faible part d'entre eux soient thermiquement excités ; dans les non-métaux, la vibration des ions est la plus importante dans ce rôle[10]. La conductivité thermique est donc liée d’une part à la conductivité électrique (mouvement des porteurs de charge) et d'autre part à la structure même du matériau (vibrations des atomes autour de leur position d'équilibre). En effet, dans un solide, les vibrations des atomes ne sont pas aléatoires et indépendantes les unes des autres, mais correspondent à des modes propres de vibration, aussi appelés « phonons » (on peut faire par exemple l’analogie avec un pendule ou une corde de guitare, dont la fréquence de vibration est fixée). Ces modes propres de vibration correspondent à des ondes qui peuvent se propager dans le matériau, si sa structure est périodique (organisée). Cette contribution est donc plus importante dans un cristal, ordonné, que dans un verre, désordonné (d’où par exemple la différence de conductivité thermique entre le diamant ci-dessus et le verre dans le tableau)[10].
Mathématiquement, la conductivité thermique λ peut donc s'écrire comme la somme de deux contributions[10] :
où :
- λe est la contribution des porteurs de charge (électrons ou trous), ou conductivité thermique électronique ;
- λp est la contribution des vibrations des atomes (phonons), ou conductivité thermique de réseau.
La contribution des porteurs de charge est liée à la conductivité électrique σ du matériau par la relation de Wiedemann-Franz[11] :
où L est appelé facteur de Lorentz[11]. Ce nombre L dépend des processus de diffusion des porteurs de charge (ce qui correspond plus ou moins à la façon dont ils sont gênés par des obstacles lors de leurs déplacements, voir aussi diffusion des ondes) ainsi que de la position du niveau de Fermi. Dans les métaux, on le considérera égal au nombre de Lorenz L0, avec :
où :
- k est la constante de Boltzmann ;
- e est la charge de l'électron.
En réalité, L varie selon la température et le métal considéré :
| Matériaux | Facteur de Lorenz[12] (× 10−8 V2 K−2) à 0 °C |
Facteur de Lorenz[12] (× 10−8 V2 K−2) à 100 °C |
|---|---|---|
| Aluminium | 2,14 | 2,19 |
| Argent | 2,31 | 2,38 |
| Bismuth | 3,53 | 3,35 |
| Cuivre | 2,20 | 2,29 |
| Fer | 2,61 | 2,88 |
| Or | 2,32 | 2,36 |
| Plomb | 2,64 | 2,53 |
| Sodium | 2,12 |
Évolution avec l'humidité[modifier | modifier le code]
Pour les matériaux de construction, qui peuvent être sujets à d'importants taux d'humidité, il existe une relation permettant de relier les conductivités du matériau sec et du matériau humide lorsque des mesures ne peuvent être réalisées. Cette relation est la suivante[13] :
où :
- k est un coefficient de dimensions ;
- H est l’humidité relative en pourcentage ;
- λ0 est la conductivité thermique du matériau sec ; λ la conductivité thermique du matériau en condition d'humidité H
- e représente la fonction exponentielle.
Mesure pour les solides[modifier | modifier le code]
État stationnaire[modifier | modifier le code]
La détermination de la conductivité thermique d’un matériau repose sur le lien entre le gradient de température et le flux de chaleur qu'il génère dans ce matériau[14]. Le principe est illustré sur la figure suivante :
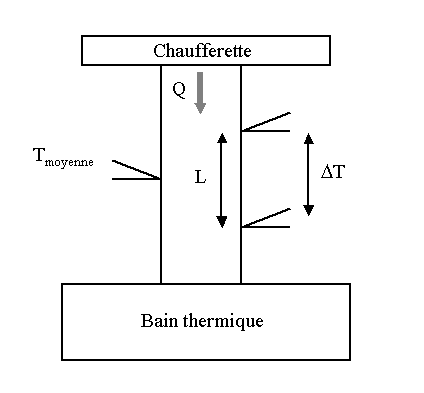
L’une des extrémités de l’échantillon de section A est fixée à un doigt froid (bain thermique) dont le rôle est d'évacuer le flux thermique traversant l'échantillon, et l’extrémité opposée à une chaufferette dissipant dans l’échantillon une puissance thermique Q obtenue par effet Joule, de manière à produire un gradient thermique suivant la longueur de l’échantillon. Des thermocouples séparés par une distance L mesurent la différence de température ΔT le long de l’échantillon. Un troisième thermocouple, calibré, est également fixé à l’échantillon pour déterminer sa température moyenne (la température de mesure). La conductivité thermique est alors donnée par[14] :
- .
Si ΔT n’est pas trop important (de l'ordre de 1 °C), la conductivité thermique mesurée est celle correspondant à la température moyenne mesurée par le troisième thermocouple. Le principe de la mesure repose alors sur l’hypothèse que la totalité du flux de chaleur passe par l’échantillon. La précision de la mesure dépend donc de la capacité à éliminer les pertes thermiques, que ce soit par conduction thermique par les fils, convection par le gaz résiduel, radiation par les surfaces de l’échantillon ou pertes dans la chaufferette : la mesure s'effectue donc dans des conditions adiabatiques[14].
Pour assurer la meilleure précision possible, l’échantillon dont on souhaite mesurer la conductivité thermique est donc placé dans une chambre de mesure sous vide (pour minimiser la convection). Cette chambre est elle-même enveloppée dans plusieurs boucliers thermiques dont la température est régulée (afin de minimiser les effets radiatifs). Enfin, les fils des thermocouples sont choisis de manière à conduire le moins possible la chaleur[14].
Étant donné qu’il est d'autant plus difficile de minimiser les pertes thermiques que la température augmente, cette technique ne permet la mesure de la conductivité thermique qu’à des températures inférieures à la température ambiante (de 2 à 200 K sans difficulté, et jusqu’à 300 K (27 °C) pour les meilleurs appareils de mesure).
Méthode dite « Laser Flash »[modifier | modifier le code]
Pour les températures supérieures à la température ambiante, il devient de plus en plus difficile d’éliminer ou de tenir compte des pertes thermiques par radiation (conditions adiabatiques), et l’utilisation de la technique à l’état stationnaire présentée ci-dessus n’est pas recommandée. Une solution est de mesurer la diffusivité thermique en lieu et place de la conductivité thermique. Ces deux grandeurs sont en effet liées par la relation :
où :
- λ(T) est la conductivité thermique en W cm−1 K−1 ;
- a(T) est la diffusivité thermique en cm2 s−1 ;
- d(T) est la masse volumique en g cm−3 ;
- Cp(T) est la capacité thermique massique en J g−1 K−1.
Si l’on suppose que la masse volumique ne varie pas avec la température, il suffit de mesurer la diffusivité thermique et la chaleur spécifique pour obtenir une mesure de la conductivité thermique à haute température.
La figure suivante schématise l’appareillage utilisé pour la mesure de conductivité thermique par la méthode dite « laser flash »[15] :
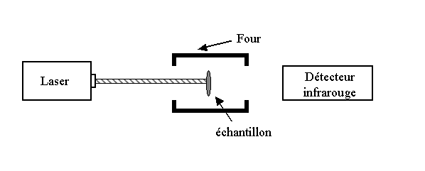
Un échantillon cylindrique dont l’épaisseur d est nettement plus faible que son diamètre est placé dans un porte-échantillon qui se trouve à l’intérieur d’un four maintenu à température constante. Une de ses faces est illuminée par des pulses (de l’ordre de la milliseconde) émis par un laser, ce qui assure un chauffage uniforme de la face avant. La température de la face arrière est mesurée, en fonction du temps, à l’aide d’un capteur de mesure infrarouge. En l’absence de pertes thermiques de l’échantillon, la température devrait augmenter de manière monotone. Dans une situation réelle, l’enregistreur mesurera un pic de température suivi d’un retour à la température du four. Le temps t nécessaire pour que la face arrière atteigne la moitié de la température de pic (par rapport à la température du four), permet de déterminer la diffusivité thermique suivant :
- avec :
- d : diamètre de l'échantillon (m)
- t : temps caractéristique (s)
Il est alors possible de calculer la conductivité thermique grâce à la masse volumique et la chaleur spécifique.
La difficulté de cette technique réside dans le choix des paramètres de mesure optima (puissance du laser et épaisseur de l'échantillon).
Dans la construction[modifier | modifier le code]
Résistance thermique d'une paroi[modifier | modifier le code]
En thermique du bâtiment, la valeur λ de la conductivité thermique entre dans le calcul de la résistance thermique d'une paroi.
Pour qualifier les matériaux hétérogènes au travers desquels la chaleur se propage en même temps par conduction, convection et rayonnement, la donnée de la conductivité thermique n'est pas suffisante. Pour les qualifier, on utilise une valeur de résistance thermique déduite d'essais en laboratoire.
Comme la conductivité thermique d'un matériau varie en fonction de la température et de l'humidité de celui-ci, les documentations technico-commerciales des matériaux doivent préciser, avec la valeur de λ, les conditions dans lesquelles cette valeur est obtenue. Cette valeur λ déclarée doit être éventuellement certifiée par un agrément technique.
D'autre part on opère une distinction entre λi, la conductivité thermique d'un matériau dans une paroi intérieure ou extérieure lorsque le matériau est protégé contre l'humidité due à la pluie ou à la condensation, et d'autre part λe, la conductivité thermique du même matériau non protégé contre cette humidité[16].
Normes et règlements[modifier | modifier le code]
En France, ont été promulguées des normes successives pour inciter les bâtisseurs à une isolation thermique maximale des bâtiments, notamment les normes RT 2000, RT 2005 et RT 2012.
Conductivités thermiques de quelques matériaux[modifier | modifier le code]

Les conductivités thermiques des substances courantes varient sur au moins quatre ordres de grandeur[17]. Les gaz ont généralement une faible conductivité thermique, tandis qu'elle est élevée pour les métaux purs. Par exemple, dans des conditions normales, la conductivité thermique du cuivre est plus de 10 000 fois supérieure à celle de l'air.
De tous les matériaux, les allotropes du carbone, tels que le graphite et le diamant, sont généralement considérés comme ayant les conductivités thermiques les plus élevées à température ambiante[18]. La conductivité thermique du diamant naturel à température ambiante est plusieurs fois plus élevée que celle d'un métal hautement conducteur comme le cuivre (bien que la valeur précise varie en fonction du type de diamant)[19].
Les conductivités thermiques de certaines substances sélectionnées sont répertoriées ci-dessous ; une liste étendue peut être trouvée dans la liste de conductivités thermiques. Ces valeurs sont des estimations illustratives seulement, car elles ne tiennent pas compte des incertitudes de mesure ou de la variabilité des définitions des matériaux.
| Substance | Conductivité thermique (W m−1 K−1) | Température (°C) |
|---|---|---|
| Air | 0.026 | 25 |
| Styrofoam[20] | 0.033 | 25 |
| Eau[21] | 0.6089 | 26.85 |
| Béton[21] | 0.92 | – |
| Cuivre[21] | 384.1 | 18.05 |
| Diamant naturel[19] | 895–1350 | 26.85 |
Métaux[modifier | modifier le code]
Les métaux ont des conductivités élevées, entre 20 et 418 watts par mètre-kelvin[22].
| Matériau | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Acier doux | 46 |
| Acier inoxydable (18 % chrome, 8 % nickel) | 16 |
| Aluminium (pureté de 99,9 %) | 237 |
| Al-SiC | 150-200 |
| Argent | 418[23] |
| Cuivre | 390[23] |
| Étain | 66,6 |
| Fer | 80[24] |
| Fonte | 50 |
| Or | 317 |
| Platine | 71,6 |
| Plomb | 35[24] |
| Titane | 20 |
| Zinc | 116 |
Pierre naturelle[modifier | modifier le code]
Les pierres naturelles employées dans la construction ont des valeurs de conductivité thermique entre 0,15 et 3,5 W m−1 K−1.
| Matériaux | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Ardoise (parallèle) | 2,50[25] |
| Ardoise (perpendiculaire) | 1,4[25] |
| Basalte | 2[25] |
| Calcaire (2 g/cm3) | 1[25] |
| Craie | 0,92[25] |
| Granite (2,8 g/cm3) | 2,2[25] |
| Grès (2,2 g/cm3) | 1,3[25] |
| Marbre | 2,08 à 2,94 |
| Mortier de chaux | 0,87 |
| Pouzzolane | 0,15 |
| Schiste | 2,2[26] |
Terre[modifier | modifier le code]
| Matériaux | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Adobe (terre crue) | 0,32 |
| Brique (terre cuite) | 0,84[23] |
| Terre (sèche) | 0,75 |
Bois[modifier | modifier le code]
À densité et humidité égales, le bois résineux est plus conducteur que le bois feuillu. Plus un bois est dense, plus il est humide et plus il est conducteur.
| Matériaux | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Aggloméré | 0,15[25] |
| Bois de chêne | 0,16[25] |
| Bois de noyer (0,65 g/cm3) | 0,14[25] |
| Bois de pin (parallèle aux fibres) | 0,36 |
| Bois de pin (perpendiculaire aux fibres) | 0,15 |
| Contreplaqué | 0,11 - 0.15[25] |
Isolants[modifier | modifier le code]
En termes de bâtiment, selon la norme française RT 2012, un matériau est considéré comme isolant si sa conductivité thermique est inférieure à 0,065 watt par mètre-kelvin[27].
| Matériaux | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Carton | 0,11 |
| Laine | 0,05 |
| Laine de bois | 0,036 - 0,042 |
| Laine de roche | 0,033 - 0,044[28] |
| Laine de verre | 0,030 - 0,046[28] |
| Liège | 0,038 - 0,042[23] |
| Mousse de polyuréthane rigide (PUR) | 0,025 |
| Mousse phénolique | 0,018 - 0,025 |
| Ouate de cellulose | 0,038 - 0,042 |
| Paille (perpendiculaire aux fibres) | 0,052[29] |
| Perlite | 0,038 |
| Polystyrène expansé (EPS) | 0,036 |
| Polyisocyanurate (PIR) | 0,023 |
| Roseau (en panneau) | 0,056 |
Dérivés du carbone[modifier | modifier le code]
Si le diamant a une conductivité thermique très élevée, celle du diamant bleu naturel l’est plus encore. On peut donc examiner des gemmes pour déterminer si elles sont de véritables diamants en utilisant un appareil de contrôle de la conductivité thermique, un des instruments standard utilisés en gemmologie[réf. nécessaire].
En conséquence, les diamants de n'importe quelle taille paraissent toujours très froids au toucher en raison de leur effusivité thermique élevée.
| Matériaux | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Carbone vitreux (1,5 g/cm3) | 4[30] |
| Charbon de bois (0,2 g/cm3) | 0,055[25] |
| Diamant | 1 000-2 600 |
| Graphène | 4 000-5 300 |
| Graphite sens plans graphène | 1 950[31] |
| Graphite sens plans graphène | 5,7[31] |
| Graphite polycristallin | 80[32] |
| Houille (1,35 g/cm3) | 0,26[25] |
Matériaux divers[modifier | modifier le code]
| Matériaux | Conductivité thermique (W m−1 K−1) à 20 °C |
|---|---|
| Air (100 kPa) | 0,0262 |
| Amiante | 0,16778 |
| Asphalte (2,1 g/cm3) | 0,06[25] |
| Bakélite (1,3 g/cm3) | 1,4[25] |
| Béton (parpaing) | 0,92[23] |
| Cuir | 0,088[réf. nécessaire] |
| Dihydrogène (gaz) | 0,18 |
| Dioxygène (gaz) | 0,027 |
| Eau | 0,6[23] |
| EPDM | 0,36 à 0,40 |
| Époxy | 0,25 |
| Hélium (gaz) | 0,14[24] |
| Nitrure de silicium | 20-65 |
| PVC (polymère) | 0,17 |
| Quartz | 6,8-12 |
| Silicium | 149 |
| Verre | 1,2[23] |
Conductivités thermiques des éléments[modifier | modifier le code]
Conductivité thermique des éléments en W cm−1 K−1 à 27 °C[33]. Certaines valeurs manquantes sont disponibles sur l'article « Conductivité thermique des solides » sur le site techniques-ingenieur.fr[2].
| H | He | |||||||||||||||||
| Li 0,847 |
Be 2 |
B | C | N | O | F | Ne | |||||||||||
| Na 1,41 |
Mg 1,56 |
Al 2,37 |
Si 1,48 |
P | S | Cl | Ar | |||||||||||
| K 1,024 |
Ca 2 |
Sc 0,158 |
Ti 0,219 |
V 0,307 |
Cr 0,937 |
Mn 0,0782 |
Fe 0,802 |
Co 1 |
Ni 0,907 |
Cu 4,01 |
Zn 1,16 |
Ga 0,406 |
Ge 0,599 |
As 0,5 |
Se | Br | Kr | |
| Rb 0,582 |
Sr 0,353 |
Y 0,172 |
Zr 0,227 |
Nb 0,537 |
Mo 1,38 |
Tc 0,506 |
Ru 1,17 |
Rh 1,5 |
Pd 0,718 |
Ag 4,29 |
Cd 0,968 |
In 0,816 |
Sn 0,666 |
Sb 0,243 |
Te | I 0,45 |
Xe | |
| Cs 0,359 |
Ba 0,184 |
* |
Lu 0,164 |
Hf 0,23 |
Ta 0,575 |
W 1,74 |
Re 0,479 |
Os 0,876 |
Ir 1,47 |
Pt 0,716 |
Au 3,17 |
Hg 0,0834 |
Tl 0,461 |
Pb 0,353 |
Bi 0,0787 |
Po 0,2 |
At | Rn |
| Fr | Ra | ** |
Lr | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Nh | Fl | Mc | Lv | Ts | Og |
| ↓ | ||||||||||||||||||
| * |
La 0,134 |
Ce 0,113 |
Pr 0,125 |
Nd 0,165 |
Pm 0,15 |
Sm 0,133 |
Eu 0,139 |
Gd 0,105 |
Tb 0,111 |
Dy 0,107 |
Ho 0,162 |
Er 0,145 |
Tm 0,169 |
Yb 0,385 | ||||
| ** |
Ac | Th 0,54 |
Pa | U 0,276 |
Np 0,063 |
Pu 0,0674 |
Am | Cm | Bk | Cf | Es | Fm | Md | No | ||||
Notes et références[modifier | modifier le code]
- Mathieu (J.P.), Kastler (A.) et Fleury (P.), Dictionnaire de la physique, Masson Eyrolles,
- Michel Laurent et Pierre-Louis Vuillermoz, Conductivité thermique des solides, Techniques de l'Ingénieur, 29 p. (lire en ligne), p. 3
- (en) U. Jarfelt et O. Ramnäs, « Thermal conductivity of polyurethane foam - best performance », 10th International Symposium on District Heating and Cooling « Sektion 6 a: Heat distribution – pipe properties », 3-5 septembre 2006 (lire en ligne [PDF], consulté le ).
- (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, (ISBN 978-0-471-40065-3), « Chap. 8: Transport Phenomena in Dilute Gases »
- (en) Carl L. Yaws, Transport Properties of Chemicals and Hydrocarbons, Amsterdam/Boston, Gulf Professional Publishing, , 715 p. (ISBN 978-0-323-28658-9)
- (en) Gilberto Medeiros Kremer, « The Methods of Chapman-Enskog and Grad and Applications », RTO-EN-AVT 194, 2011 [1]
- (en) Georges Duffa, Ablative Thermal Protection System Modeling, AIAA, , 431 p. (ISBN 978-1-62410-171-7)
- Touloukian 1970.
- Romuald Saint-Martin, Croissance cristalline, structure et propriétés de transport thermique des cuprates unidimensionnels Sr2CuO3, SrCuO2 et La5Ca9Cu24O41 (thèse de doctorat en chimie), université Paris-Sud, , 201 p. (résumé), p. 135.
- « Les propriétés thermiques », De l'atome à l'objet, université Paris Sciences et Lettres (consulté le ).
- « Qu’est-ce que la loi Wiedemann – Franz – Nombre de Lorenz – Définition », sur thermal-engineering.org, (consulté le ).
- G. W. C. Kaye et T. H. Laby, Table of Physical and Chemical Constants, Éditions Longmans Green, Londres, 1966
- Pierre Delot, « Conductivité thermique », sur ballederiz.fr/, (consulté le )
- Dalila Bounoua, Synthèse et études de cuprates de basse dimensionnalité à propriétés thermiques fortement anisotropes, Université Paris-Saclay, , 360 p. (lire en ligne), p. 172,173
- A. Degiovanni, Diffusivité thermique et méthode flash, vol. 185, Revue générale de thermique, , p. 420-422
- « Conductivité thermique des matériaux (λ) », sur energieplus-lesite.be (consulté le )
- (en) Michael J. Heap, Alexandra R.L. Kushnir, Jérémie Vasseur, Fabian B. Wadsworth, Pauline Harlé, Patrick Baud, Ben M. Kennedy, Valentin R. Troll et Frances M. Deegan, « The thermal properties of porous andesite », Journal of Volcanology and Geothermal Research, vol. 398, , p. 106901 (ISSN 0377-0273, DOI 10.1016/j.jvolgeores.2020.106901
 , Bibcode 2020JVGR..39806901H, S2CID 219060797).
, Bibcode 2020JVGR..39806901H, S2CID 219060797).
- (en) Boston College, « An unlikely competitor for diamond as the best thermal conductor », sur Phys.org, (consulté le ).
- (en) John R. Rumble (dir.), CRC Handbook of Chemistry and Physics, Boca Raton, CRC Press/Taylor & Francis, , 99e éd., « Thermal Conductivity in W cm−1 K−1 of Metals and Semiconductors as a Function of Temperature ».
- « Conductivité thermique des matériaux et gaz courants », sur engineeringtoolbox.com.
- Bird, Stewart et Lightfoot 2006, p. 270-271.
- « Conductivité et propriétés des métaux », sur tibtech.com (version du sur Internet Archive).
- J. Ph. Pérez et A. M. Romulus, Thermodynamique, fondements et applications, Masson, p. 155
- Harris Benson, Physique, t. 1 : Mécanique, Saint-Laurent, Québec, Éditions du Renouveau Pédagogique, , 3e éd., p. 519.
- Handbook of Chemistry and Physics
- Pompeo et Gueret, « CONDUCTIVITE THERMIQUE DES MATERIAUX » [PDF], (consulté le )
- Dimitri Molle et Pierre-Manuel Patry, RT 2012 et RT existant : Réglementation thermique et efficacité énergétique, Éditions Eyrolles, (lire en ligne)
- « Recherche multicritères », sur ACERMI (consulté le ).
- Réseau Français de la Construction Paille, « Caractéristiques techniques », sur rfcp.fr (consulté le )
- « Carbone vitreux pour l'industrie et le laboratoire » [PDF], sur Mersen (consulté le )
- « Propriétés et structure des céramiques », sur IUT en ligne
- « Graphite polycristallin — Conductivité Thermique », sur Netsch
- (en) David R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, , 90e éd., 2804 p., Relié (ISBN 978-1-4200-9084-0)
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) Yeram Sarkis Touloukian, P. E. Liley et S. C. Saxena, Thermal Conductivity. Nonmetallic Liquids and Gases, vol. 3, IFI/Plenum Press, (ISBN 0-306-67023-2).
 Compilation contenant de nombreuses données fiables.
Compilation contenant de nombreuses données fiables.
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Conductivité thermique d'un matériau (λ) sur le site energieplus-lesite.be de Architecture et Climat de l'Université catholique de Louvain.
- Conductivité thermique des matériaux (λ) sur le site energieplus-lesite.be de Architecture et Climat de l'Université catholique de Louvain.
- Attestations de valeurs lambda sur un site de Plate-forme Maison Passive asbl.


















































