Densité

Pour les articles homonymes, voir Densité (homonymie).

La densité ou densité relative d'un corps est le rapport de sa masse volumique à la masse volumique d'un corps pris comme référence. Le corps de référence est l'eau pure à 4 °C pour les liquides et les solides. Pour les liquides, une mesure précise de densité utilise un pycnomètre. Dans le cas de gaz ou de vapeur, le corps de référence gazeux est l'air, à la même température et sous la même pression. La densité est une grandeur sans dimension et sa valeur s'exprime sans unité de mesure.

Histoire et terminologie

La densité d'un corps est une notion de physique ancienne, apparue au XVII^e siècle. Cette grandeur caractéristique d'un corps, exprimée par un nombre sans dimension a un usage commun. Elle est souvent définie dans les dictionnaires savant ou encyclopédique.

Émile Littré définit la densité comme le « rapport de la masse d'un corps à son volume », c'est-à-dire comme la masse volumique. Le scientifique rationaliste Laplace, admirateur de Newton, cité en référence, utilise en 1810 la densité en synonyme de masse volumique. Le BIPM lui-même associe encore, en 1960, les termes densité et masse volumique.

Néanmoins la mesure expérimentale directe de la masse volumique s'appuie toujours sur une pesée hydrostatique avec comme référence une masse d'eau liquide. C'est une mesure de densité relative. La « densité relative » étant la seule grandeur mesurable expérimentalement sa forme courte « densité » est généralement préférée. Le mot « densité » est, d'après Littré, l'expression moderne du terme « densité relative », expression toujours utilisée en anglais (relative density). La masse volumique reste le synonyme moderne des expressions désuètes « densité absolue » ou « densité propre » (appelée density, sous-entendu absolute density, en anglais).

Enfin, il ne faut pas confondre la densité d'un corps, sans dimension, avec la densité particulaire, définie par une unité, puisque cette dernière densité d'une grandeur est un rapport statistique d'une population donnée sur un élément d'espace (longueur, surface ou volume) utilisé pour décompter cette population, comme c'est le cas pour la densité surfacique de population, la densité de charge, la concentration molaire.

Expression de la densité

La densité, notée d, s'exprime de la sorte :

$d= \frac{\rho_{\rm corps}}{\rho_{\rm ref}}$

où $\rho_{\rm corps}$ est la masse volumique du corps considéré, et $\rho_{\rm ref}$ est la masse volumique du corps de référence.

Densité des gaz

La densité des gaz est calculée à partir de la densité de l'air. La valeur de référence prise est la masse d'un litre d'air à 0 °C sous une pression de 760 mmHg, soit 1,29349 g.

On a ainsi $d_{gaz}=\frac {\rho_{gaz}} {\rho_{air}}$

Il existe une façon commode de relier la masse molaire M d'un gaz et sa densité. En effet, en considérant un gaz parfait, $PV=nRT$ d'où :

$V=\frac{nRT}{P}=\frac {mRT}{MP}$ avec $n=\frac {m}{M}$

On a donc $M=\frac{m}{V}.{\frac{RT}{P}}$ ou $M=\rho.\frac{RT}{P}$

et $d_{gaz}=\frac{\rho_{gaz}}{\rho_{air}}=\frac{M_{gaz}}{M_{air}}$ avec $\frac{RT}{P}$ pris identique pour l'air et le gaz considéré.

En tenant compte de la composition de l'air et des masses molaires respectives (78 % de diazote, 21 % de dioxygène et 1 % d'argon environ), il est facile de montrer que : $M_{air} = 29g.mol^{-1}$, soit $M_{gaz}=29 g.mol^{-1}*d$

Par exemple, la densité du dihydrogène (M = 2 g.mol^{-1}) est $d_{H_{2}}=\frac {M_{H_{2}}}{29} = \frac {2}{29}$

Soit $d_{H_{2}}=0,069$ environ.

Il découle de cette relation que plus un gaz a une masse molaire élevée, plus il est dense. Il est ainsi facile de prévoir que le dioxyde de carbone (CO₂) sera plus dense que l'air (40/29~1,38) et que les gaz les moins denses sont le dihydrogène et l'hélium (environ 2/29~0,07 pour les deux).

Le composé gazeux le plus dense à température ambiante est l'hexafluorure de soufre, SF₆ (d = 146/29 ~ 5,03).

Densité pour les solides et les liquides

Le plus souvent, l'eau est utilisée comme corps de référence pour la densité des liquides et des solides. Dans ce cas, la masse volumique de l'eau est prise égale à 1 000 kg/m³ (ou à 1 kg/dm³, ou à 1 kg/L, ou encore 1 g/cm³). Il s'agit de la masse volumique de l'eau à 3,98 °C et à pression atmosphérique. En effet, l'eau possède une particularité parmi les liquides : sa densité et sa masse volumique sont maximales, non pas à sa température de fusion (0 °C) comme la plupart des liquides, mais à 3,98 °C, or en métrologie, le fait de prendre comme référence une propriété physique qui passe par un extremum est très intéressant : au voisinage de cet extremum la propriété physique varie très peu. Ainsi au voisinage de 3,98 °C, une imprécision sur la détermination de la température exacte affecte très peu la masse volumique de l'eau et donc le résultat d'une mesure de densité.

La densité devient :

$d= \frac{\rho_{\rm corps}}{\rho_{\rm eau}}$

où $\rho_{\rm corps}$ est la masse volumique du corps considéré et $\rho_{\rm eau}$ est la masse volumique de l'eau (1 000 kg/m³).

Pour corriger les valeurs mesurées à d'autres températures que la température de référence, il faut exploiter la courbe de variation de la masse volumique de l'eau en fonction de la température pour en déduire la masse volumique des matériaux à la température des mesures.

Mesure de la densité relative d'un solide

La densité relative d'un corps solide par rapport à un corps fluide est le rapport de la masse du corps solide sur la masse du corps fluide de volume identique à celui du corps solide. Mesurons cette densité relative en réalisant trois pesées et en immergeant le solide. Les mesures doivent être réalisées dans les mêmes conditions de pression et de température (souvent les conditions normales: 76 cm de mercure, 0°C).

• Corps solide:

Fig.A: Première pesée

Un corps solide $\scriptstyle \mathcal C_1$ est accroché au plateau d'une balance à l'aide d'une tige rigide $\scriptstyle t$ de masse $\scriptstyle M_t$ inconnue (figure A). La masse $\scriptstyle m_1$ et le volume $\scriptstyle \mathcal V_1$ du corps $\scriptstyle \mathcal C_1$ ne sont pas connus. Une tare $\scriptstyle T$, de masse $\scriptstyle M_T$ inconnue, est posée sur l'autre plateau de la balance. Les masses inconnues des deux plateaux de la balance sont notées $\scriptstyle M_1$ et $\scriptstyle M_2$.

L'équilibre du fléau de la balance est réalisé grâce à la présence d'un poids, de masse $\scriptstyle M_A$ connue, posée sur le plateau au quel est accroché le corps $\scriptstyle \mathcal C_1$ (à l'extrémité A du fléau).

La force $\scriptstyle F_A$ s'exerçant au niveau de l'extrémité A du fléau est égale à:

$\scriptstyle F_A \;=\; m_1 \; g \;+\; M_t \; g \;+\; M_A \; g \;+\; M_1 \; g \;\;\;\; (A)$

où $\scriptstyle g$ est l'accélération de la pesanteur.

• Masse du corps solide

Fig.B: Deuxième pesée

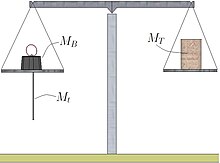
Décrochons le corps $\scriptstyle \mathcal C_1$ (figure B). Afin d'équilibrer de nouveau le fléau de la balance, déposons la masse $\scriptstyle M_A$ et remplaçons la par une masse $\scriptstyle M_B$. La force $\scriptstyle F_A$ s'exerçant au niveau de l'extrémité A du fléau est égale à:

$\scriptstyle F_A \;=\; M_t \; g \;+\; M_B \; g \;+\; M_1 \; g \;\;\;\; (B)$

Puisque le fléau a retrouvé sa position d'équilibre, les forces $\scriptstyle F_A$ données par les égalités (A) et (B) sont égales, d'où:

$\scriptstyle F_A \;=\; m_1 \; g \;+\; M_t \; g \;+\; M_A \; g \;+\; M_1 \; g \;=\; M_t \; g \;+\; M_B \; g \;+\; M_1 \; g \;\;\;\; (C)$

La masse $\scriptstyle m_1$ du corps $\scriptstyle \mathcal C_1$ est donc égale à:

$\scriptstyle m_1 \;=\; M_B \;-\; M_A \;\;\;\; (D)$

• Densité relative du corps solide

Fig.C: Troisième pesée

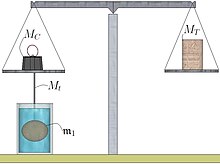
Le corps $\scriptstyle \mathcal C_1$ est de nouveau suspendu au plateau (figure C). Mais, cette fois-ci, il est plongé dans un liquide de masse volumique $\scriptstyle \rho_L$ (normalement de l'eau distillée). Afin d'équilibrer la balance, la masse $\scriptstyle M_B$ est déposée et une masse $\scriptstyle M_C$ est installée à sa place. Le liquide exerce une force sur le corps $\scriptstyle \mathcal C_1$. Il s'agit de la poussée d'Archimède. C'est une force dont la direction est verticale et dont le sens est dirigée vers le haut. Son module est égale à $\scriptstyle \Pi \;=\; \rho_L \; \mathcal V_1 \; g$.

La force $\scriptstyle F_A$ s'exerçant au niveau de l'extrémité A du fléau est égale à:

$\scriptstyle F_A \;=\; m_1 \; g \;+\; M_t \; g \;+\; M_C \; g \;-\; \underbrace{\scriptstyle \rho_{L} \; \mathcal V_1 \; g}_{\Pi} \;+\; M_1 \; g \;\;\;\; (E)$

Puisque le fléau a retrouvé sa position d'équilibre, les forces $\scriptstyle F_A$ données par les égalités (A) et (E) sont égales, d'où:

$\scriptstyle m_1 \; g \;+\; M_t \; g \;+\; M_A \; g \;+\; M_1 \; g \;=\; m_1 \; g \;+\; M_t \; g \;+\; M_C \; g \;-\; \rho_{L} \; \mathcal V_1 \; g \;+\; M_1 \; g \;\;\;\; (F)$

Donc:

$\scriptstyle \Pi \;=\; \rho_{L} \; \mathcal V_1 \; g \;=\; M_C \; g \;-\; M_A \; g \;\;\;\; (G)$

Le module $\scriptstyle \Pi \;=\; \rho_{L} \; \mathcal V_1 \; g$ de la poussée d'Archimède est assimilable au poids d'un corps liquide: le poids du liquide déplacé par le corps solide $\scriptstyle \mathcal C_1$. Nommons $\scriptstyle \mathcal C_2$ ce corps liquide. Le volume, la masse volumique et la masse du corps $\scriptstyle \mathcal C_2$ sont donc respectivement égales à:

$\scriptstyle \mathcal V_2 = \mathcal V_1 \;\;\; et \;\;\; \rho_2 = \rho_L$

$\scriptstyle m_2 \;=\; \rho_2 \; \mathcal V_2 \;=\; \rho_L \; \mathcal V_1 \;=\; \frac{\Pi}{g} \;=\; M_C \;-\; M_A \;\;\; (H)$

En tenant compte des égalités (D) et (H), nous pouvons donc déterminer la densité relative du corps solide $\scriptstyle \mathcal C_1$ par rapport au corps fluide $\scriptstyle \mathcal C_2$:

$d_{1/2} \;=\; \frac{m_1}{m_2} \;=\; \frac{\rho_1 \; \mathcal V_1}{\rho_2 \; \mathcal V_2} \;=\; \frac{\rho_1 \; \mathcal V_1 }{\rho_2 \; \mathcal V_1} \;=\; \frac{\rho_1 }{\rho_2} \;=\; \frac{M_B - M_A}{M_C - M_A} \;\;\;\; (I)$

Densité et flottabilité

Comparaison de deux corps avec densités supérieure et inférieure à un.

La densité peut indiquer la flottabilité d'un corps par rapport à l'eau douce. En effet, si la densité d'un corps est supérieure à 1 comme pour une vis métallique (voir illustration) le corps en question coule dans l'eau. À l'inverse, si la densité d'un corps est inférieure à 1 comme pour un bouchon de liège (voir illustration) le corps en question flotte sur l'eau. Dans l'eau de mer ou une solution saline à gradient de salinité, ces chiffres sont à ajuster.

Cas particulier de l'eau liquide

D'une manière générale quand un corps liquide refroidit sa densité augmente et devient maximale à la température de solidification. De plus le corps solide est généralement plus dense que le corps liquide. L'eau fait exception : sa densité maximale est atteinte non pas à 0 °C mais à 3,98 °C et la glace est moins dense que l'eau liquide. Cette anomalie dilatométrique permet à l'eau tiède, à l'eau très froide et à la glace de flotter sur de l'eau à 3,98 °C.

Parmi les métaux moins denses à l'état solide qu'à l'état liquide, on peut citer le bismuth et le plutonium. Cela pose des problèmes importants lors du moulage, à cause du gonflement qui accompagne la solidification.

Densité des principaux métaux utilisés

Métaux usuels symbole densité Platine Pt 21,5 Or Au 19,3 Mercure Hg 13,56 Plomb Pb 11,35 Argent Ag 10,5 Bismuth Bi 9,82 Cuivre Cu 8,78 Nickel Ni 8,27 Fer Fe 7,87 Etain Sn 7,29 Zinc Zn 7,1 Aluminium Al 2,7 Magnésium Mg 1,43 Sodium Na 0,97 Source : Gaston Tissandier Densité et flottation des minerais métalliques Les minerais qui contiennent de fortes teneurs en métaux lourds ou les métaux denses à l'état natif dispersés dans une gangue peuvent être séparés facilement des impuretés terreuses par effet de masse ou d'inertie, c'est-à-dire de moindre entraînement, dans un flux d'eau sur un plan incliné. C'est la séparation gravimétrique. D'autres minerais, plus légers, peuvent être rendus flottables à l'aide de savons ou corps tensioactifs spécifiques dans des bains plus ou moins agités. Ce sont les procédés industriels de flottation. Densité des liquides biologiques en médecine Les densités ne servent que rarement en sciences médicales. Dans un ouvrage de référence, on ne trouve que le liquide sudoral du test de mucoviscidose et le liquide d'épanchement séreux. L'essentiel des données est exprimé en concentrations massique ou molaire. Il est fréquent, fruit de la confusion avec la terminologie anglo-saxonne exposée plus haut, que ce qui soit appelé densité des urines, du sang ou de tout liquide biologique, soit simplement la masse volumique exprimée en g/L du liquide. Ainsi, la densité du sang que l'on peut lire sur les résultats de laboratoire est supérieure à 1000 (g/L). Notes et références Articles connexes Glossaire des minéraux Minéralogie Pétrographie Densimètre électronique Liens externes Densité d'une particule de matière fluide ou solide