Décroissance exponentielle

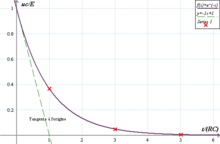
La décharge d'un condensateur est une décroissance exponentielle.

Une quantité est dite sujette à une décroissance exponentielle si elle diminue à un taux proportionnel à sa valeur. Mathématiquement, cela peut être exprimé par l'équation différentielle suivante, avec N la quantité et λ un nombre positif appelé la « constante de décroissance » :

$\dfrac{dN \left( t \right) }{dt} = -\lambda N \left( t \right).$

La solution de cette équation est, en notant N₀ la valeur de N à l'instant t = 0 :

$N \left( t \right) = N_0 e^{-\lambda t}. \,$

Démonstration

Remarque : si λ est négatif, on a plutôt croissance exponentielle du phénomène.

On part de la définition sous forme d'une équation différentielle :

$\dfrac{dN \left( t \right) }{dt} = -\lambda N \left( t \right)$

En séparant les variables, on obtient :

$\dfrac{dN \left( t \right) }{N \left( t \right)} = -\lambda dt.$

Alors, en intégrant entre l'instant initial et t :

$\int_{0}^{t} \dfrac{dN \left( t' \right) }{N \left( t' \right)} = \int_{0}^{t} -\lambda dt'$

Ce qui s'intègre en :

$ln \left[ N \left( t \right) \right] - ln \left[ N_0 \right] = - \lambda t$

Soit enfin :

$N \left( t \right) = N_0 e^{-\lambda t}$

Quantités dérivées

Durée de vie moyenne

Si on considère que la quantité N qui décroît est discrète, c'est-à-dire que N mesure le nombre d'élément d'un ensemble, alors on peut donner une expression de la durée de vie moyenne d'un élément dans cet ensemble :

$\tau = \dfrac{1}{\lambda}$

On l'appelle aussi « constante de temps ». N vérifie alors :

$N(t) = N_0 e^{-t/\tau} \,$

Demi-vie

Il est plus courant de faire usage de la demi-vie d'un système à décroissance radioactive, qui correspond à la durée au bout de laquelle la quantité N est divisée par 2. On note souvent cette durée t_{1 / 2}. Elle est reliée à la constante de décroissance et à la constante de temps par les relations :

$t_{1/2} = \dfrac{\ln 2}{\lambda} = \tau \ln 2$

On peut également remplacer l'exponentielle de l'expression de la demi-vie pour obtenir :

$N(t) = N_0 2^{-t/t_{1/2}} \,$

Utilisation

En physique, la décroissance exponentielle est caractéristique des phénomènes sans vieillissement, c'est-à-dire qui se produisent avec une égale probabilité quelle ait été leur durée de vie, par exemple dans le suivi de la désintégration radioactive. On retrouve cette décroissance à travers de nombreuses observations physiques comme par exemple dans les variations de pression entre deux contenants ou la décharge électrique d'un condensateur.

En biologie, une telle décroissance peut modéliser l'élimination d'un produit dans le sang, au cours du temps.

Voir aussi

Articles connexes

• Radioactivité, Décroissance radioactive ;
• Croissance exponentielle ;
• Demi-vie.