Discriminant
Réalisant
En mathématiques, le discriminant noté , ou le réalisant noté [1], est une notion algébrique. Il est utilisé pour résoudre des équations du second degré. Il se généralise pour des polynômes de degré > 0 quelconque et dont les coefficients sont choisis dans des ensembles munis d'une addition et d'une multiplication. Le discriminant apporte dans ce cadre une information sur l'existence ou l'absence de racine multiple.
Le discriminant est utilisé dans d'autres domaines que celui de l'étude des polynômes. Son usage permet de mieux comprendre les coniques et les quadriques en général. On le retrouve dans l'étude des formes quadratiques ou celle des corps de nombres dans le cadre de la théorie de Galois ou celle des nombres algébriques. Sa définition se fonde sur le calcul d'un déterminant.
Historique[modifier | modifier le code]
L'histoire et la découverte du discriminant est un élément de l'histoire plus générale de l'algèbre et en particulier de la résolution des équations du second degré. Il apparait notamment lorsqu'on résout ces équations à l'aide d'identités remarquables.
Polynôme du second degré[modifier | modifier le code]
Résolution de l'équation à coefficients réels[modifier | modifier le code]
Considérons une équation du second degré, ici , et sont trois coefficients réels tel que est différent de zéro :
Discriminant de l'équation du deuxième degré — Le discriminant (ou réalisant[1]) de l'équation précédente est le nombre (ou ) défini par :
La connaissance du discriminant permet de résoudre l'équation :
Résolution de l'équation — Si le discriminant est positif, l'équation admet deux solutions et données par les formules suivantes :
Si le discriminant est nul, les deux solutions obtenues sont égales, on dit que l'équation admet une racine double :
Si le discriminant est strictement négatif, il n'a pas de racine carrée réelle et donc l'équation n'admet pas de solution réelle.
Dans ce dernier cas, le discriminant a toutefois une racine complexe et donc une solution complexe.
Résolution de l'équation à solutions ou coefficients complexes[modifier | modifier le code]
Si les solutions nombres complexes de l'équation sont admises, ou si les coefficients , et sont complexes[2], la situation est un peu différente. Le théorème de d'Alembert-Gauss précise qu'il existe toujours au moins une solution à l'équation. Dans l'ensemble des complexes, un nombre admet toujours deux racines carrées, il existe une valeur telle que son carré soit égal à :
Racines complexes — L'équation admet deux solutions et données par les formules suivantes :
Si le discriminant est nul, la même solution apparait deux fois : l'équation admet une racine double égale à :
Discriminant réduit[modifier | modifier le code]
Le discriminant réduit apparait quand on écrit l'équation du second degré sous la forme :
par un changement de variable . Dans ce cas les 2 et 4 apparaissant dans l’expression des solutions et du discriminant se simplifient et on obtient :
Discriminant réduit — Le discriminant réduit de l'équation précédente est le nombre défini par :
L'expression des racines, si elles existent, devient :
Exemples[modifier | modifier le code]
Cherchons à résoudre l'équation suivante :
Le calcul du discriminant et des racines et donne :
Dans le cas de l'équation suivante, le discriminant réduit est nul et il n'existe qu'une racine, égale à –3.
Le dernier exemple décrit une situation où le discriminant est strictement négatif, ici égal à –3. On remarque de est une racine carrée du discriminant, si désigne l'unité imaginaire. Ceci permet de déterminer les solutions :
On peut remarquer que ces deux racines sont des racines de l'unité : elles ont pour cube (pour puissance troisième) le nombre 1. Le polynôme choisi est un cas particulier de polynôme cyclotomique.
Le nombre d'or est l'unique solution positive de l'équation : ici , donc .
Interprétation géométrique[modifier | modifier le code]
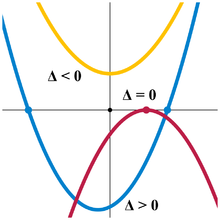
L'équation définit (pour non nul) une parabole, et rechercher la solution revient à rechercher l'intersection de cette parabole avec l'axe des abscisses. Le discriminant permet de savoir si cette intersection existe, selon les trois possibilités illustrées par l'image en haut de l'article :
- courbe bleue (discriminant positif) : la parabole croise deux fois l'axe des abscisses ; pour entre les deux solutions, a le signe opposé à , et le même signe que à l'extérieur ;
- courbe rouge (discriminant nul) : la parabole tangente l'axe des abscisses en un point unique (la solution double) ;
- courbe jaune (discriminant négatif) : la parabole ne croise pas l'axe des abscisses, est toujours du même signe que .
Forme quadratique en dimension 2[modifier | modifier le code]
Sur l'ensemble des nombres réels, une forme quadratique en dimension 2 associe à deux variables et un nombre à l'aide de la formule suivante :
Une forme quadratique possède aussi une expression matricielle :
Le déterminant de l'expression matricielle est égal à ; on retrouve une expression proche de la précédente. Un changement de base, à l'aide d'une matrice de passage modifie la valeur du déterminant. Plus exactement la valeur dans la nouvelle base est égale à la valeur dans l'ancienne base que multiplie le carré du déterminant de , le signe du déterminant reste invariant. Cette propriété est analysée dans l'article détaillé.
Pour cette raison, il existe trois définitions différentes du discriminant d'une forme quadratique en dimension deux. Le discriminant d'une forme quadratique dans une base est le déterminant de la matrice associée à la forme quadratique dans la base . L'analogie avec la situation précédente permet de définir le discriminant de la forme quadratique comme étant égal à . Enfin, comme le seul invariant associé au déterminant de la forme quadratique, le discriminant est aussi défini comme le signe du déterminant qui peut prendre les valeurs +1, 0 ou –1.
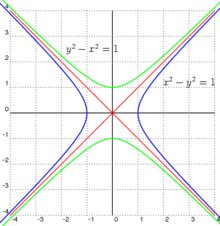
Le discriminant sépare les formes quadratiques en trois familles. En dimension deux, avec pour définition du discriminant la valeur du déterminant dans la base canonique, si le discriminant est de signe positif pour une valeur donnée l'ensemble des points vérifiant correspond à une ellipse ou à l'ensemble vide. Si le discriminant est nul, alors l'ensemble correspond à une parabole. Si le discriminant est négatif, est une hyperbole. Les formes quadratiques permettent ainsi d'obtenir les trois différentes formes de coniques.
Polynôme de degré quelconque[modifier | modifier le code]
L'extraction de racine d'un polynôme à l'aide du discriminant ne se généralise pas aux degrés supérieurs à deux. Le discriminant d'un polynôme garde néanmoins une utilité.
Dans le cas des équations de degré deux, le discriminant est nul si et seulement si le polynôme possède une racine multiple. L'existence de racine multiple peut avoir d'importantes conséquences. En algèbre linéaire, la présence de racine multiple dans le polynôme minimal d'un endomorphisme modifie sa nature. Cette présence interdit la diagonalisation. Sur les extensions des nombres rationnels, les polynômes irréductibles, c'est-à-dire qui ne sont pas factorisables, n'ont jamais de racine multiple (cf. l'article Extension séparable), cette situation n'est pas vraie pour tous les corps. Dans le cadre de la théorie de Galois, cette distinction est importante, les résultats sont différents selon la configuration.
Définition et propriétés[modifier | modifier le code]
La généralisation du discriminant d'un polynôme de degré quelconque offre un outil permettant de déterminer si ses racines sont simples ou multiples. Dans ce paragraphe désigne un anneau intègre et un polynôme de degré dont les coefficients appartiennent à et sont notés de la manière suivante :
La dérivée formelle de est notée , elle existe même si est différent du corps des nombres réels ou complexes. Enfin désigne le résultant ; c'est une application particulière qui à deux polynômes associe un élément de .
- Le discriminant de , en général noté , est la valeur définie par la formule suivante[3] lorsque (ce qui est toujours le cas en caractéristique 0) :
Le coefficient de normalisation possède son importance ; un discriminant peut ainsi être également interprété comme un volume orienté. L'usage d'une telle approche devient évidente lors de l'analyse du discriminant d'une forme quadratique ou d'un anneau de Dedekind dans le cadre de la théorie algébrique des nombres.
Certains résultats de la théorie de Galois s'appliquent au discriminant, il faut alors étendre l'anneau des coefficients. Comme est commutatif unitaire intègre, il possède un corps des fractions commutatif et peut être considéré comme un polynôme à coefficients dans . Ici désigne le corps de décomposition de , c'est-à-dire le plus petit corps contenant et toutes les racines de , à un isomorphisme près. Le discriminant possède la propriété suivante :
- Le discriminant du polynôme est non nul si et seulement si est séparable (c'est-à-dire n'admet aucune racine multiple).
Ce résultat est une conséquence d'une propriété générale du résultant de deux polynômes : il est non nul si et seulement si les deux polynômes sont premiers entre eux. Il peut aussi se déduire de la formule suivante :
- Soit pour variant de 1 à , les racines du polynôme , le discriminant vérifie l'égalité suivante[4] :
Exemples[modifier | modifier le code]
Le discriminant d'un polynôme de degré 1 est toujours égal à 1.
Pour les polynômes du second degré et avec les notations du premier paragraphe, on obtient :
en caractéristique différente de 2.
Pour les polynômes de degré trois on considère généralement le polynôme normalisé, c'est-à-dire celui dont le monôme dominant est égal à 1. Avec les notations suivantes :
on obtient, si [6] :
L'expression est un peu complexe ; pour cette raison, la tradition est de réaliser des substitutions. On obtient le résultat général suivant : supposons que est un corps commutatif de caractéristique différente de 2 et de 3. Alors on peut mettre le polynôme unitaire sous la forme :
Dans le cas d'une équation polynomiale de degré 3 à coefficients réels, si ce discriminant est strictement positif, l'équation admet trois solutions réelles distinctes, si ce discriminant est nul, une racine est multiple et toutes sont réelles, si ce discriminant est strictement négatif, l'équation n'admet qu'une solution réelle, les deux autres sont complexes conjuguées. Par exemple, pour l'équation binomiale , ce discriminant vaut si est un réel non nul.
Les solutions de l'équation sur un corps commutatif de caractéristique différente de 2 et de 3 sont données par la « formule de Cardan » qu'on peut, dans une clôture algébrique de , mettre sous la forme
où est le discriminant noté ci-dessus et est une racine cubique primitive de l'unité. Les deux termes et de cette somme sont liés par la relation [7]. On trouvera un exemple de résolution d'équation du troisième degré en caractéristique finie à l'article Méthode de Cardan.
Les courbes elliptiques sont un cas particulier de polynômes du troisième degré à deux variables. Pour le cas simple d'une courbe elliptique de la forme , où les coefficients sont des nombres réels, le discriminant est de nouveau défini par [8].
Expression générale[modifier | modifier le code]
L'expression générale du discriminant du polynôme défini par :
est la suivante :
et après simplification du coefficient sur la première ligne du déterminant, afin d'obtenir une définition valable sur tout anneau commutatif :
Utilisations du discriminant[modifier | modifier le code]
Revenons sur l'utilisation du discriminant.
- Dans le cas d'équations du second ou du troisième degré, le discriminant permet de calculer les racines et son signe permet de les caractériser (cf. supra).
- Considérons plus généralement un polynôme à coefficients réels de degré . Si les racines de ce polynôme sont toutes réelles et distinctes, son discriminant vérifie . Si , les racines de sont distinctes et deux d'entre elles au moins sont complexes conjuguées. Plus généralement, soit un corps commutatif et un polynôme de degré . Si les racines de dans une clôture algébrique de appartiennent à , le discriminant est un carré dans .
- Soit un corps commutatif et un polynôme de degré . Ce polynôme est séparable si, et seulement si son discriminant est (voir supra).
- Soit un corps commutatif de caractéristique , un polynôme séparable de degré , son corps de décomposition, et les racines de dans . Les conditions suivantes sont équivalentes[9] :
- (a) Le groupe de Galois , en tant que groupe des permutations de , est inclus dans le groupe alterné .
- (b) appartient à .
- (c) Le discriminant est un carré dans .
Discriminant d'un anneau d'entiers algébriques[modifier | modifier le code]
La théorie algébrique des nombres utilise la notion de discriminant à partir d'une définition qui semble bien différente. Elle correspond à un déterminant d'une forme quadratique et s'applique à un anneau commutatif . Les deux définitions sont néanmoins intimement corrélées. S'il existe un entier algébrique tel que l'anneau est égal à — ici désigne les entiers relatifs — alors le polynôme minimal de est à coefficients dans . Son discriminant au sens des polynômes est égal au discriminant de l'anneau au sens de la théorie algébrique des nombres.
Notes et références[modifier | modifier le code]
- « Equation du second degré » sur le site de l'UCLouvain.
- Cette situation se rencontre par exemple dans l'étude des circuits électriques : l'impédance est un nombre complexe.
- Cette définition est fréquente. On la trouve, par exemple dans (en) Eric W. Weisstein, « Polynomial Discriminant », sur MathWorld (sous une forme plus générale dans le cas où n'est pas de degré ) ou encore Résultant et discriminant sur le site bibmath.net. Cependant dans Résultant. Discriminant sur le site les-mathematiques.net, le coefficient de normalisation est absent.
- (en) Granino A. Korn et Theresa M. Korn, Mathematical Handbook for Scientists and Engineers : Definitions, Theorems, and Formulas for Reference and Review, Dover, (réimpr. 2000), 2e éd. (1re éd. 1961), 1152 p. (ISBN 978-0-486-32023-6, lire en ligne), p. 16.
- Issue de (en) R. W. D. Nickalls et R. H. Dye, « The geometry of the discriminant of a polynomial », The Mathematical Gazette, vol. 80, , p. 279-285 (lire en ligne).
- Cette formule se trouve par exemple dans l'article (en) Discriminant de l'Encyclopædia Britannica.
- Il convient en effet d'associer correctement deux à deux les racines cubiques dans une clôture algébrique du corps : voir H. Weber, « Formule de Cardan modifiée par Cayley », Nouvelles annales de mathématiques, 3e série, vol. 14, , p. 347-349 (lire en ligne). La restriction sur la caractéristique de provient des divisions par 2 et par 3 : voir Mac Lane et Birkhoff 1999, §XIII.1.
- Les conventions sont parfois différentes, et on peut trouver dans la littérature cette expression multipliée par un nombre strictement positif.
- Cohn 2005, Thm. 7.10.5.
Bibliographie[modifier | modifier le code]
- Nicolas Bourbaki, Algèbre, Chapitres 4 à 7, Springer, , 432 p. (ISBN 3-540-34398-9).
- (en) Paul Moritz Cohn, Basic Algebra, Springer, , 480 p. (ISBN 81-8128-047-4).
- Serge Lang, Algèbre [détail des éditions].
- (en) Saunders Mac Lane et Garrett Birkhoff, Algebra, AMS, , 3e éd., 626 p. (ISBN 0-8218-1646-2, lire en ligne).
- Pierre Samuel, Théorie algébrique des nombres [détail de l’édition].
- Daniel Perrin, Cours d'algèbre [détail des éditions].
- (en) Robert J. Walker, Algebraic curves, Springer, 1978 (ISBN 978-03-879-0361-3).















































































![{\displaystyle P(X)\in A[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8747232fb8265d01aa2816ea465cbd03a340349a)
















![{\displaystyle {\begin{aligned}\Delta &=(r+{\rm {i}}s-r+{\rm {i}}s)^{2}(r+{\rm {i}}s-t)^{2}(r-{\rm {i}}s-t)^{2}\\&=(2is)^{2}[(r-t+{\rm {i}}s)(r-t-{\rm {i}}s)]^{2}\\&=-4s^{2}[(r-t)^{2}-({\rm {i}}s)^{2}]^{2}\\&=-4\left(s[(r-t)^{2}+s^{2}]\right)^{2}<0\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c36be3e783e9d994040ddbe3dc6491009e26b7cb)

![{\displaystyle {\rm {j}}^{k}{\sqrt[{3}]{{1 \over 2}\left(-q+{\sqrt {\frac {-\Delta }{3^{3}}}}\right)}}+{\rm {j}}^{-k}{\sqrt[{3}]{{1 \over 2}\left(-q-{\sqrt {\frac {-\Delta }{3^{3}}}}\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcbcc4d49d6d9b482b01a68421e00dd3b5463b9c)
















![{\displaystyle f\left(X\right)\in k\left[X\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/728f1bf13fea709b86bbef24ecd8da005ee6e70a)
















![{\displaystyle \mathbb {Z} [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c23b4b8c0940351292a63f482325eb80ecb52696)

