Intégrale multiple

Intégrale simple comme superficie délimitée par une courbe, deux droites $x=a$ et $x=b$, et l'axe des abscisses.

Intégrale multiple comme volume situé entre une surface et sa projection $D$ sur le repère $(O,x,y)$.

Intégrale multiple comme volume situé entre un domaine du plan et son image (la surface) par une fonction.

L'intégrale multiple est une forme d'intégrale qui s'applique aux fonctions de plusieurs variables réelles.

À l'instar des intégrales simples, les intégrales multiples possèdent des interprétations géométriques significatives. Limitons-nous pour commencer aux fonctions à valeurs réelles positives. Tandis que l'intégrale définie de fonctions d'une variable représente la mesure de l'aire délimitée par leur courbe représentative, l'axe des abscisses et les deux droites à ses bornes d'intégration (d'équations respectives $x=a$ et $x=b$), l'intégrale de fonctions de deux variables (intégrale double) représente le volume délimité par leur surface représentative et le domaine d'intégration $D$.

En général, les intégrales de fonctions de trois variables (intégrales triples) sont interprétables comme des mesures d'hypervolumes, soit de solides à 4 dimensions, donc non représentables graphiquement.

Dans l'exemple à droite, le volume du parallélépipède $P$ de côtés 4 ; 6 et 5 peut se calculer de deux manières :

1. Par l'intégrale double ∬_D 5 dxdy de la fonction constante $f$ définie par $f(x,y) = 5$ évaluée dans l'« intervalle à deux dimensions » $D$ (région appartenant au plan $xy$). Dans ce cas, le volume est calculé comme la somme de tous les volumes de section infinitésimale et de hauteur 5.
2. Par l'intégrale triple ∭_P 1 dxdydz de la fonction constante $f$ définie par $f(x,y,z)=1$ évaluée dans l'« intervalle à trois dimensions » $P$ coïncidant avec le parallélépipède même. Dans ce cas, le volume total est calculé comme la somme de tous les volumes infinitésimaux du domaine $P$.

Ces résultats coïncident tous avec la valeur V = 4 × 6 × 5 = 120, comme nous le verrons par la suite.

Dans le cadre des fonctions à plusieurs variables, donc d'intégrales multiples, on ne parle que d'intégrales définies, dans le sens où il est impossible de donner une primitive de telles fonctions.

Définition formelle

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Article détaillé : intégrale de Riemann.

Soit f : T → ℝ, T ⊂ ℝⁿ une fonction mesurable. Soit donc δ le plus grand diamètre d'une partition finie $P = \{T_i\}_{i=1}^p$ de T. Soit $P_i$ un point de $T_i$, pour i ∈ {1, ..., p}. Alors, si

$I = \lim_{\delta\to0} \sum_{i=1}^p f(P_i)\, \operatorname{mes}(T_i)$

existe (et est indépendant de la succession de partitions choisie et des points $P_i$), $I$ est appelé intégrale multiple de $f$ sur $T$ (ici $\mathrm{mes}(T_i)$ est la mesure de $T_i$) et est notée :

$\int\!\dots\!\int_T f(x_1,\dots,x_n)\;\mathrm dx_1\dots\mathrm dx_n$

Intégrale double

Dans le cas où T ⊆ ℝ² , on appelle et note par

$\iint_T f(x,y)\;\mathrm dx\,\mathrm dy$

l'intégrale double de $f$ sur $T$.

Intégrale triple

De la même manière, si T ⊆ ℝ³,

$\iiint_T f(x,y,z)\;\mathrm dx\,\mathrm dy\,\mathrm dz$

est appelée l'intégrale triple de $f$ sur $T$.

Dans les applications pratiques, comme l'ingénierie ou la physique appliquée, on rencontre quasi exclusivement des intégrales doubles et triples, outre les simples.

Propriétés

Article détaillé : Intégration (mathématiques)#Propriétés des intégrales.

Les mêmes propriétés que pour les intégrales simples sont valables ; à savoir la linéarité, la monotonie, la valeur absolue et le théorème de la moyenne.

Linéarité

Soient $f$ et $g$ deux fonctions continues et bornées, $D$ un sous-ensemble ouvert borné de ℝⁿ. Pour tout couple de nombres réels $\alpha$ et $\beta$, on a :

$\int\!\dots\!\int_D (\alpha f+\beta g)(x_1,\dots,x_n)\;\mathrm dx_1\dots\mathrm dx_n$ $=\alpha \int\!\dots\!\int_D f(x_1,\dots,x_n)\;\mathrm dx_1\dots\mathrm dx_n\ +\ \beta\int\!\dots\!\int_D g(x_1,\dots,x_n)\;\mathrm dx_1\dots\mathrm dx_n$.

Théorème de la moyenne

Soit f : D → ℝ une fonction continue ; alors, si D est compact et connexe, il existe un élément $(m_1,m_2,...,m_n)$ de $D$ tel que

$f(m_1,...,m_n) = \frac{1}{\operatorname{mes}D} \iint_D f(x_1,\dots,x_n)\;\mathrm dx_1\dots\mathrm dx_n$

Cette valeur est appelée « valeur moyenne » ou « moyenne intégrale » de $f$ sur $D$.

Méthodes d'intégration

La résolution des calculs d'intégrales multiples consiste la plupart du temps à reformuler ces intégrales en une série d'intégrales simples, les seules directement calculables.

Examen direct

Dans certains cas particuliers, il est possible d'éviter le calcul et d'obtenir immédiatement le résultat.

Fonctions constantes

Dans le cas de fonctions constantes qui associent $c$ à tout élément de ℝⁿ, le résultat est immédiat : vu que $c$ est la valeur moyenne de la fonction, il suffit de multiplier la mesure du domaine par la constante $c$. Le résultat est égal dans ℝ² au volume du cylindre de hauteur $c$ et de génératrice la frontière du domaine, et dans ℝ³ à son hypervolume.

Exemple (voir introduction) :

$D = \{ (x,y) \in \R^2 \mid 2 \le x \le 6 \ ; \ 2 \le y \le 8 \}$ et $f(x,y) = 5$
$\iint_Df(x,y)\;\mathrm dx\,\mathrm dy= \operatorname{mes}\,D \cdot 5 = (6-2)\cdot(8-2) \cdot 5 = 120$

Exploitation des symétries

Dans les cas de domaines pour lesquels sont présentes des symétries selon certains axes et que la fonction présente une imparité pour la variable correspondante, l'intégrale s'annule.

Exemple 1 :

Soit $f(x,y) = 2\sin(x) - 3y^3 + 5$ et C = {(x,y) ∈ ℝ² | x² + y² ≤ 1} le domaine d'intégration (disque de rayon 1 centré à l'origine, bord inclus). Exploitant la linéarité de l'intégration, l'on peut le décomposer en trois parties :

$\iint_C \left\{2 \sin(x) - 3 y^3 + 5\right\}\mathrm dx\,\mathrm dy = \iint_T 2 \sin(x)\;\mathrm dx\,\mathrm dy - \iint_T 3 y^3\;\mathrm dx\,\mathrm dy + \iint_T 5\;\mathrm dx\,\mathrm dy$

Tant x → 2 sin(x) que y → 3y³ sont impaires, et il est évident que le disque C présente une symétrie selon x et y ; par conséquent, ces deux intégrales s'annulant, la seule contribution au résultat est celle de la fonction constante 5.

Exemple 2 :

Soit la fonction $f(x,y,z) = x\exp(y^2 + z^2)$ avec pour domaine d'intégration la sphère de rayon 2 centrée à l'origine. Le domaine présente une symétrie selon les trois axes, mais il suffit celle selon $x$, variable selon laquelle la fonction est impaire, pour annuler toute l'intégrale.

Réduction à des intégrales simples

La réduction en intégrales simples utilise le concept de domaine simple, de façon à exprimer l'intégrale en une composition d'intégrales simples. L'intégration est effectuée de l'intérieur vers l'extérieur, chaque fois par rapport à une seule variable en considérant les autres constantes – de la même façon que pour le calcul de dérivées partielles.

Domaines simples dans ℝ²

Domaine simple défini par les courbes $C_1(x)$, $C_3(x)$ et les droites $x=a$ et $x=b$.

Soient $a$ et $b$ deux nombres réels, et $y_1(x)$ et $y_2(x)$ les deux fonctions continues (éventuellement par morceaux) de $]a,b[$ vers ℝ – telles que ∀x ∈ ]a,b[, y₁(x) < y₂(x) – qui définissent un domaine $D$ mesurable et borné :

$D = \{(x,y)\in\R^2\mid a\leqslant x\leqslant b,\ y_1(x) \leqslant y \leqslant y_2(x)\}$.

On appelle ce domaine un domaine simple (ou défini par des conditions simples) « orthogonal » à l'axe $x$, car au moins une de ses bornes (ici les deux droites d'équation $x=a$ et $x=b$) est perpendiculaire à l'axe des $x$.

On définit de la même manière un domaine orthogonal à l'axe $y$ en définissant des fonctions $x_1(y)$, $x_2(y)$ et deux nombres $a$ et $b$ tels que ∀y ∈ ]a,b[, x₁(y) < x₂(y) :

$D = \{(x,y)\in\R^2\mid a\leqslant y\leqslant b,\ x_1(y) \leqslant x \leqslant x_2(y)\}$.

Théorème

Théorème — Pour toute fonction $f$, continue sur un domaine simple $D$ orthogonal à $x$, on a :

$\iint_D f(x,y)\ \mathrm{d}x\mathrm{d}y = \int_{x_1}^{x_2}\left(\int_{y_1(x)}^{y_2(x)} f(x,y)\mathrm{d}y\right)\mathrm{d}x$.

Pour plus de commodité, on note :

$\int_{x_1}^{x_2}\left(\int_{y_1(x)}^{y_2(x)} f(x,y)\mathrm{d}y\right)\mathrm{d}x = \int_{x_1}^{x_2}\mathrm{d}x\int_{y_1(x)}^{y_2(x)} f(x,y)\mathrm{d}y\quad\text{ou}\quad\int_{x_1}^{x_2}\!\int_{y_1(x)}^{y_2(x)} f(x,y)\mathrm{d}y\mathrm{d}x$.

De la même manière, si $D$ est défini orthogonal à $y$,

$\iint_D f(x,y)\ \mathrm{d}x\mathrm{d}y = \int_{y_1}^{y_2}\mathrm{d}y\int_{x_1(y)}^{x_2(y)} f(x,y)\mathrm{d}x$.

Ce résultat s'étend aux fonctions d'un nombre quelconque de variables.

On le voit, l'ordre des intégrations n'importe pas, pour peu qu'on ait défini le domaine en adéquation. C'est une conséquence directe du théorème de Fubini.

Domaine simple défini par $y_1(x) = x^2$ et $y_2(x) = 1$, pour ]a,b[ = ]0,1[.

Exemple  :

Soit $D = \{ (x,y) \mid x>0, y<1, y>x^2 \}$ (voir dessin). On se propose de calculer :

$\iint_D (x+y) \;\mathrm{d}x\mathrm{d}y$.

Ce domaine est perpendiculaire tant à $x$ qu'à $y$. Pour pouvoir le définir en conditions simples, on cherche les deux fonctions et les deux nombres réels qui définissent ses bornes. Dans ce cas les fonctions sont $y_1(x) = x^2$ et $y_2(x) = 1$ et le domaine est donné par l'intersection des fonctions avec la droite $x = 0$ et leur point d'intersection $(x,y)=(1,1)$. On a donc $[a,b] = [0,1]$. Appliquons le théorème, en commençant par intégrer selon $y$ :

$\iint_D (x+y) \;\mathrm{d}x\mathrm{d}y = \int_0^1\mathrm{d}x\int_{x^2}^1(x+y)\mathrm{d}y = \int_0^1 \mathrm{d}x \left[xy + \frac{y^2}{2}\right]^1_{x^2}$

On aboutit à une simple intégrale définie :

$\int_0^1 \left[xy + \frac{y^2}{2} \right]^1_{x^2} \mathrm dx = \int_0^1 \left(x + \frac{1}{2} - x^3 - \frac{x^4}{2}\right) \; \mathrm{d}x = \ldots = \frac{13}{20}$.

Si on avait choisi de définir le domaine par rapport à $y$, on aurait obtenu l'expression :

$\iint_D (x+y) \;\mathrm{d}x\mathrm{d}y = \int_0^1\mathrm{d}y\int_0^{\sqrt{y}} (x+y)\mathrm{d}x$

conduisant au même résultat.

Domaines simples dans ℝ³

L'extension aux intégrales triples est immédiate. Considérons un domaine $T$ défini par des conditions simples

$T = \{(x,y,z)\in\R^3\mid x_1(z,y) < x < x_2(z,y), y_1(z) < y < y_2(z), z_1 < z < z_2\}$.

On a :

$\iiint_T f(x,y,z)\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = \int_{z_1}^{z_2}\!\int_{y_1(z)}^{y_2(z)}\!\int_{x_1(z,y)}^{x_2(z,y)}f(x,y,z)\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z$

La définition est analogue pour les 5 autres cas d'orthogonalité dans ℝ³. De manière générale, le nombre de points de vue possibles dans ℝⁿ est donné par la factorielle de $n$.

Domaine orthogonal au plan $xy$ dans ℝ³

Exemple  :

Considérons un domaine $T$ de ℝ³ orthogonal au plan $xy$ (voir dessin)

$T =\,$ $\,\{(x,y,z)\mid \alpha(x,y)<z<\beta(x,y), a<y<b, f(y)<x<g(y)\}$.

Sa projection sur $xy$ est un domaine $D$ de ℝ² défini orthogonal à $y$ par $D = \{ (x,y)\in\R^2\mid a<y<b, f(y)<x<g(y)\}$.

$\iiint_T f(x,y,z)\;\mathrm{d}x \mathrm{d}y \mathrm{d}z = \iint_D \mathrm{d}x \mathrm{d}y \int_{\alpha (x,y)}^{\beta (x,y)} f(x,y,z) \;\mathrm{d}z$

Changement de variables

Article connexe : intégration par changement de variable.

Souvent, lorsque les méthodes précédentes ne sont pas efficaces (domaine difficile à exprimer ou fonction difficile à intégrer), on a recours à un changement de variables afin de reformuler l'intégrale de façon plus commode. Il s'ensuit que :

• La fonction doit être réécrite selon la transformation ;
• Idem pour le domaine, car il est délimité par des fonctions dépendantes des variables de départ auxquelles on a appliqué la transformation ;
• Le nouvel intégrande dépend de la valeur absolue du déterminant de la matrice jacobienne (le jacobien) contenant les dérivées partielles de la transformation selon les nouvelles variables.

Changement de variables dans une intégrale multiple — Soient $D$ et $E$ deux sous-ensembles ouverts bornés de ℝⁿ et $\Phi(u_1,...,u_n)$ une bijection de classe $C^1$ de $E$ sur $D$ dont le jacobien $\det J_\Phi$ ne s'annule pas. Alors pour toute fonction continue et bornée f : D → ℝ on a :

$\int\!\!\dots\!\!\int_D f(x_1,\ldots,x_n) \;\mathrm dx_1\ldots\mathrm dx_n = \int\!\!\dots\!\!\int_E f\bigl(\Phi(u_1,\ldots,u_n) \bigr)\left|\det J_\Phi(u_1,\ldots,u_n)\right|~\mathrm du_1\ldots\mathrm du_n$.

Coordonnées polaires

Passage d'un secteur annulaire de coordonnées cartésiennes à polaires

Dans ℝ², si le domaine présente une symétrie circulaire (c-à-d décrit un secteur annulaire) et que la fonction a des caractéristiques particulières, l'on peut appliquer une transformation en coordonnées polaires ; c'est-à-dire que les points en coordonnées cartésiennes sont réexprimés en coordonnées polaires. Cela permet de changer la forme du domaine et de faciliter l'intégration.

D'après la définition de ce système de coordonnées, la transformation à effectuer est :

$(x,y) \longrightarrow (r\cos\theta,r\sin\theta)$.

Exemple  :

Soit $f(x,y) = x^2 + y^2$. Dans ce cas, $f(r, \theta) = r^2 (\cos \theta^2 + \sin \theta^2) = r^2$ (grâce aux identités trigonométriques, très utiles dans ces calculs).

Réexpression du domaine

La transformation du domaine s'effectue en exprimant la longueur des rayons du secteur annulaire et l'ampleur de l'angle décrit, afin de définir les intervalles de $r$ et $\theta$ à partir de $x$ et $y$.

Exemple  :

Considérons D = {(x,y) | x² + y² ≤ 4}, soit un disque de rayon 2 ; il est évident que l'angle décrit est celui d'un tour complet. Ainsi, $\theta$ variera de 0 à $2\pi$ et $r$ de 0 à 2.

Exemple  :

Passage d'un anneau des coordonnées cartésiennes aux polaires

Considérons D = {(x,y) | 4 ≤ x² + y² ≤ 9, y ≥ 0}, soit une demi-couronne de rayon extérieur 3 et de rayon intérieur 2 (voir dessin), limitée aux $y$ positifs ; on voit que $\theta$ varie de 0 à $\pi$ et $r$ de 2 à 3. Par conséquent, le domaine transformé en coordonnées polaires est le rectangle T = {(r,θ) | 2 < r < 3, 0 < θ < π}.

Jacobien, intégration

Comme indiqué précédemment, le passage en coordonnées polaires est le changement de variables $(x,y)\to(\phi,\Psi)=(r\cos\theta,r\sin\theta)$. Les nouvelles variables sont l'angle $\theta$ et le rayon $r$, et les fonctions $\phi(r,\theta)~$ et $\Psi(r,\theta)~$ sont celles qui les associent à $x$ et $y$. On peut donc définir formellement cette transformation par l'application suivante :

$(\phi,\Psi) : \begin{array}{rcl} F & \longrightarrow & E\\ (r,\theta) & \longmapsto & \bigl(\phi(r,\theta),~\Psi(r,\theta)\bigr) = (r\cos\theta,~r\sin\theta) \end{array}$

La matrice jacobienne de l'application au point $(r,\theta)$ est :

$\frac{\part(\phi,\Psi)}{\part(r,\theta)}(r,\theta) = \begin{bmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \\ \end{bmatrix}$

Le jacobien du passage en coordonnées polaires est donc $r \cos^2(\theta)+r \sin^2(\theta) = r$ et on a :

$\iint_E f(x,y) \;\mathrm dx\mathrm dy = \iint_F f(r\cos\theta,r\sin\theta)r \;\mathrm dr\mathrm d \theta$

Exemple  :

Soit $f(x,y) = x$ à intégrer sur le domaine de l'exemple précédent (r ∈ [2,3] et θ ∈ [0,π]). Transformons la fonction :

$f(x,y) = x \longrightarrow f(r,\theta) = r\cos \theta$;

puis appliquons la formule pour l'intégration :

$\iint_D x \;\mathrm dx\mathrm dy = \iint_T r\cos\theta\,r\;\mathrm dr\mathrm d \theta = \iint_T r^2\cos\theta\;\mathrm dr\mathrm d \theta$.

Enfin :

$\int_0^\pi\mathrm d\theta\int_2^3 r^2\cos\theta\;\mathrm dr = \int_0^\pi\cos\theta\;\mathrm d\theta \left[ \frac{r^3}{3}\right]_2^3 = [\sin\theta]_0^\pi \left(9 - \frac{8}{3}\right) = 0$.

Exemple  :

Soit $f(x,y)=h$ à intégrer sur $D = \{(x,y)\mid x^2 + y^2 \le R^2\}$, c'est-à-dire un disque de rayon $R$. Le rayon $r$ varie donc de 0 à $R$ et $\theta$ de 0 à $2\pi$. Il vient :

$\int_0^R \int_0^{2\pi} hr\;\mathrm dr \mathrm d\theta = \int_0^Rhr\;\mathrm dr \int_0^{2\pi}\mathrm d\theta = \left[h\frac{r^2}{2}\right]_{0}^{R}\bigl[\theta\bigr]_0^{2\pi} =h\frac{R^2}{2} 2\pi=\pi hR^2$

Où l'on retrouve la formule classique pour le calcul du volume du cylindre.

Coordonnées cylindriques

Système de coordonnées cylindriques

Dans ℝ³, l'intégration sur des domaines ayant une base circulaire peut s'effectuer via un passage en coordonnées cylindriques :

$(x,y,z) \longrightarrow (r\cos\theta,r \sin \theta, z)$

La réexpression du domaine n'est pas difficile compte tenu que seule la forme de la base du domaine change, tandis que le développement tridimensionnel du domaine suit l'original.

Exemple  :

Soit D = {(x,y,z) | 4 ≤ x² + y² ≤ 9, 0 ≤ z ≤ 5} (le tube de rayon compris entre 2 et 3 et d'hauteur 5). Après transformation, l'on obtient le domaine T = {(r,θ,z) | 2 ≤ r ≤ 3, 0 ≤ θ ≤ 2π, 0 ≤ z ≤ 5} (le parallélépipède de largeur comprise entre 2 et 3, de longueur $2\pi$ et de hauteur 5).

Vu que la composante $z$ reste inchangée durant la transformation, le jacobien est le même que lors du passage en coordonnées polaires, et l'on a :

$\iiint_D f(x,y,z) \;\mathrm{d}x \mathrm{d}y \mathrm{d}z = \iiint_T f(r \cos \theta, r\sin \theta, z) r \;\mathrm{d}r \mathrm{d}\theta \mathrm{d}z$

Il est conseillé d'utiliser cette méthode dans les cas de domaines cylindriques, coniques, ou tout du moins de régions pour lesquelles il est commode tant de délimiter l'intervalle des $z$ que de transformer la base circulaire et la fonction.

Exemple  :

Soit $f(x,y,z) = x^2 + y^2 + z$ à intégrer sur le cylindre D = { (x,y,z) | x² + y² ≤ 9, -5 ≤ z ≤ 5}. La transformation de $D$ en coordonnées cylindriques est la suivante :

$T = \{ (r,\theta,z)\mid 0 \le r \le 3, \ 0 \le \theta \le 2 \pi, \ -5 \le z \le 5 \}$

tandis que la fonction devient

$f(r,\theta, z) = r^2 + z$

Appliquons la formule :

$\iiint_D x^2 + y^2 +z \ \mathrm{d}x \mathrm{d}y \mathrm{d}z = \iiint_T (r^2 + z) r \ \mathrm{d}r \mathrm{d}\theta \mathrm{d}z$;

En développant :

$\int_{-5}^5 \mathrm{d}z \int_0^{2 \pi} \mathrm{d} \theta\int_0^3 r^3 + r z\; \mathrm{d}r = 2 \pi \int_{-5}^5 \left[ \frac{r^4}{4} + \frac{r^2}{2}z \right]_0^3 \mathrm{d}z$ $= 2 \pi \int_{-5}^5 \left( \frac{81}{4} + \frac{9}{2} z\right) \mathrm{d}z = 2 \pi \left[ \frac{81}{4}z + \frac{9}{4}z^2 \right]^5_{-5} = 405 \pi$.

Coordonnées sphériques

Système de coordonnées sphériques

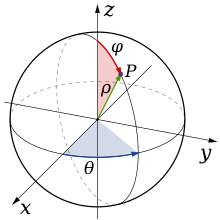
Certains domaines de ℝ³ présentent une symétrie sphérique, ainsi il est possible d'exprimer les coordonnées de leurs points à l'aide de deux angles $\theta$ (longitude) et $\phi$ (colatitude ou zénith) et d'une distance à l'origine $\rho$. Le passage en coordonnées sphériques est la transformation :

$(x,y,z) \longrightarrow (\rho \cos \theta \sin \phi, \rho \sin \theta \sin \phi, \rho \cos \phi)$

Notons que les points appartenant à l'axe $z$ n'ont pas de détermination unique dans ce système, donc $\phi$ ne peut varier que de 0 à $\pi$.

Le domaine d'intégration le plus adapté à cette transformation est évidemment la sphère.

Exemple  :

Soit $D = \{ (x,y,z) / x^2 + y^2 + z^2 \leq 16 \}$ (sphère de rayon 4 centrée à l'origine). En coordonnées sphériques, celui-ci s'exprime comme $T = \{ (\rho, \theta, \phi)\, | \,0\, \leq\, \rho\, \leq 4,\; 0 \,\leq\, \theta\, \leq\, 2\pi,\; 0\, \leq\, \phi\, \leq\, \pi \}$.

Le jacobien de cette transformation $\Phi$ est le suivant :

$\det J_\Phi (\rho,\theta,\phi)= \begin{vmatrix} \cos \theta \sin \phi & -\rho \sin \theta \sin \phi & \rho \cos \theta \cos \phi \\ \sin \theta \sin \phi & \rho \cos \theta \sin \phi & \rho \sin \theta \cos \phi \\ \cos \phi & 0 & -\rho \sin \phi \end{vmatrix} = -\rho^2 \sin \phi.$

Dès lors, on a (en se rappelant qu'il faut prendre la valeur absolue du jacobien) :

$\iiint_D f(x,y,z) \;\mathrm{d}x \mathrm{d}y \mathrm{d}z = \iiint_T f(\rho \cos \theta \sin \phi, \rho \sin \theta \sin \phi, \rho \cos \phi)\,\rho^2 \sin \phi \;\mathrm{d} \rho \mathrm{d} \theta \mathrm{d} \phi$

Il est conseillé d'utiliser cette méthode dans le cas de domaines sphériques et de fonctions facilement simplifiables à l'aide des identités trigonométriques étendues à ℝ³ (voir l'exemple suivant) ; dans les autres cas il est souvent conseillé de recourir au passage en coordonnées cylindriques, comme nous le verrons ci-après.

Exemple  :

Soit $f(x,y,z) = x^2 + y^2 + z^2$ à intégrer sur le même domaine $D$ que dans l'exemple précédent. La transformation de la fonction est très simple :

$f(\rho \cos \theta \sin \phi, \rho \sin \theta \sin \phi, \rho \cos \phi) = \rho^2~$,

tandis que nous connaissons déjà le domaine reformulé en coordonnées sphériques :

$T = \{(\rho,\theta,\phi)\mid 0 \le \rho \le 4, 0 \le \theta \le 2 \pi, 0 \le \phi \le \pi\}$.

Appliquons donc la formule pour l'intégration :

$\iiint_D x^2 + y^2 +z^2 \;\mathrm{d}x \mathrm{d}y \mathrm{d}z = \iiint_T \rho^2 \,\rho^2\sin\phi \;\mathrm{d}\rho\mathrm{d}\theta\mathrm{d}\phi$;

développons :

$\iiint_T \rho^4\sin\theta \;\mathrm{d}\rho\mathrm{d}\theta\mathrm{d}\phi = \int_0^\pi \sin\theta\mathrm{d}\theta \int_0^4 \rho^4\mathrm{d}\rho \int_0^{2\pi} \mathrm{d} \phi = 2 \pi \int_0^\pi \sin \theta\left[ \frac{\rho^5}{5}\right]_0^4 \;\mathrm{d} \theta$$= 2 \pi \left[ \frac{\rho^5}{5} \right]_0^4 \;[- \cos \theta ]_0^\pi = 4 \pi \cdot \frac{1024}{5} = \frac{4096 \pi}{5}$.

Exemple  :

Soit $D$ la sphère de rayon $3a$ (D = {(x,y,z) | x² + y² + z² ≤ 9a²}) et $f(x,y,z) = x^2 + y^2$.
En observant le domaine, il pourrait sembler commode d'adopter un passage en coordonnées sphériques ; en effet la transformation du domaine est immédiate :

$T=\{(\rho,\theta,\phi)\mid0 \le \rho \le 3a, \ 0 \le \theta \le 2 \pi, \ 0 \le \phi \le \pi\}$.

Toutefois, la transformation de la fonction mène à :

$f(x,y,z) = x^2 + y^2 \longrightarrow \rho^2 \sin^2 \theta \cos^2 \phi + \rho^2 \sin^2 \theta \sin^2 \phi = \rho^2 \sin^2 \theta$.

En appliquant la formule, on obtiendrait :

$\iiint_T \rho^2 \sin^2 \phi\,\rho^2 \sin \phi \;\mathrm{d} \rho \mathrm{d} \theta \mathrm{d} \phi = \iiint_T \rho^4 \sin^3 \phi \;\mathrm{d} \rho \mathrm{d} \theta \mathrm{d} \phi$,

ce qui est compliqué à calculer (On linéarise le sinus, ou on isole un sinus pour obtenir un sinus au carré pour passer au cosinus carré et intégrer à vue) . Le problème se résout en passant en coordonnées cylindriques. Les nouveaux intervalles du domaine deviennent :

$0 \le \rho \le 3a, \ 0 \le \phi \le 2 \pi, \ - \sqrt{9a^2 - \rho^2} \le z \le \sqrt{9a^2 - \rho^2}$.

L'intervalle des $z$ a été obtenu en résolvant l'inéquation dans la définition de $D$ (et en transformant directement $x^2+y^2$ en $\rho^2$). La nouvelle fonction est simplement $\rho^2$. Appliquons la formule :

$\iiint_T \rho^2 \rho \;\mathrm{d} \rho \mathrm{d} \phi \mathrm{d}z$,

développons :

$\int_0^{2 \pi} \mathrm{d} \phi \int_0^{3a} \rho^3 \mathrm{d} \rho \int_{- \sqrt{9a^2 - \rho^2} }^{\sqrt{9 a^2 - \rho^2} } \mathrm{d}z = 2 \pi \int_0^{3a} 2 \rho^3 \sqrt{9 a^2 - \rho^2} \ \mathrm{d} \rho$.

Pour parfaire le calcul, posons le changement de variable suivant :

$9 a^2 - \rho^2 = t \ \Rightarrow\ \mathrm{d}t = -2 \rho \mathrm{d} \rho \ \Rightarrow\ \mathrm{d} \rho = \frac{\mathrm{d} t}{- 2 \rho}$

(l'intervalle d'intégration devient $[9 a^2, 0]$). On a :

$- 2 \pi \int_{9 a^2}^{0} \rho^2 \sqrt{t} \mathrm{d}t$ ;

vu que $\rho^2 = 9 a^2 - t$, il vient :

$-2 \pi \int_{9 a^2}^0 (9 a^2 - t) \sqrt{t} \mathrm{d}t$ ;

en intervertissant les bornes d'intégration et distribuant les termes entre parenthèses, l'intégrale peut se décomposer en deux parties facilement calculables :

$2 \pi\left[ \int_0^{9 a^2} 9 a^2 \sqrt{t} \;\mathrm{d}t - \int_0^{9 a^2} t \sqrt{t} \;\mathrm{d}t\right] = 2 \pi \left[9 a^2 \frac{2}{3} t^{ \frac{3}{2} } - \frac{2}{5} t^{ \frac{5}{2}}\right]_0^{9 a^2}$ $= 2 \cdot 27 \pi a^5 \left( 6 - \frac{18}{5}\right) = 54 \pi \frac{12}{5} a^5 = \frac{648 \pi}{5} a^5$.

Exemples d'applications : calculs de volumes

Article détaillé : Volume et calcul intégral

Grâce aux méthodes décrites précédemment, il est possible de démontrer les règles de calcul du volumes de certains solides.

Cylindre  :

Considérons comme domaine la base circulaire de rayon $R$ et comme fonction la hauteur constante $h$, et appliquons directement le passage en coordonnées polaires.

$V = \int_0^{2 \pi} \mathrm{d} \phi \int_0^r h \rho \;\mathrm{d} \rho = h 2 \pi\left[ \frac{\rho^2}{2} \right]_0^R = \pi R^2 h$

ce qui correspond bien à la formule Volume = aire de base · hauteur = πR² · h.

Boule  :

Encore plus rapide, intégrons la fonction constante 1 sur la boule de rayon $R$ :

$V = \int_0^{2 \pi} \mathrm{d} \phi \int_0^\pi \sin \theta \mathrm{d} \theta \int_0^R \rho^2 \mathrm{d} \rho =$ $2 \pi \int_0^\pi \sin \theta \frac{R^3}{3} \mathrm{d} \theta = \frac{2}{3} \pi R^3 \bigl[ - \cos \theta\bigr]_0^\pi = \frac{4}{3} \pi R^3$

Tétraèdre  :

Tétraèdre

Le volume du tétraèdre, avec un sommet à l'origine et des arêtes génératrices de longueur ℓ placées le long des trois axes, peut être calculé grâce aux formules de réduction en considérant, par exemple, l'orthogonalité selon le plan $xy$ et l'axe $x$ :

$V = \int_0^\ell \mathrm{d}x \int_0^{\ell-x}\!\mathrm{d}y \int_0^{\ell-x-y}\!\mathrm{d}z = \int_0^\ell \mathrm{d}x \int_0^{\ell-x} (\ell - x - y)\;\mathrm{d}y$$= \int_0^\ell \left( \ell^2 - 2\ell x + x^2 - \frac{ (\ell-x)^2 }{2} \right) \mathrm{d}x = \ell^3 - \ell \ell^2 + \frac{\ell^3}{3} - \left[ \frac{\ell^2}{2} - \ell x + \frac{x^2}{2} \right]_0^\ell$$= \frac{\ell^3}{3} - \frac{\ell^3}{6} = \frac{\ell^3}{6}$,

ce qui correspond bien à la formule Volume = ⅓ · aire de base · hauteur = ⅓ · ℓ²/2 · ℓ = ℓ³ / 6.

Intégrale multiple impropre

Exemple de domaine impropre

Article connexe : intégrale impropre.

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Dans le cas de domaines illimités ou d'intégrandes illimités d'un côté quelconque du bord du domaine, on parle d'intégrale multiple impropre.

Si une fonction est non nulle, l'intégrale converge ou diverge à l'infini.

Références

• Jacques Douchet et Bruno Zwahlen, Calcul différentiel et intégral : Fonctions réelles de plusieurs variables réelles, Presses polytechniques et universitaires romandes, 2004, 2^e édition (1^re éd. 1998), (ISBN 2-88074-257-9).