Mécanique céleste
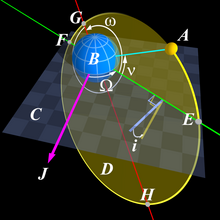
La mécanique céleste décrit le mouvement d'objets astronomiques tels que les étoiles et planètes à l'aide de théories physiques et mathématiques.
Les domaines de la physique les plus directement concernés sont la cinématique et la dynamique (classique ou relativiste).
Histoire[modifier | modifier le code]
Dans l'Antiquité, on distingue la mécanique céleste de la mécanique terrestre, les deux mondes étant considérés comme étant régis par des lois complètement différentes (ici-bas, les « choses » « tombent », là-haut elles se « promènent »). Cette conception s'intègre à la conception ptoléméenne du géocentrisme.
En astronomie, les lois de Kepler décrivent les propriétés principales du mouvement des planètes autour du Soleil. Elles sont découvertes par Johannes Kepler à partir des observations et mesures de la position des planètes ; ces lois se généralisent à tous les objets célestes. Les deux premières lois de Kepler sont publiées en 1609 et la troisième en 1618.
Peu après, en 1687, Isaac Newton, à partir des lois de Kepler, découvre la loi universelle de la gravitation, ou gravitation.
Au début du XXe siècle, Albert Einstein généralise la gravitation en l'incluant dans sa théorie de la relativité générale.
Bibliographie[modifier | modifier le code]
Ouvrages d'initiation[modifier | modifier le code]
Accessibles à partir du premier cycle universitaire.
- Florin Diacu et Philip Holmes ; Celestial Encounters - The Origins of Chaos, Princeton University Press (1996), (ISBN 0-691-00545-1). L'origine du « chaos » moderne se trouve dans les travaux pionniers d'Henri Poincaré réalisés à la fin du XIXe siècle à propos d'un vieux problème de mécanique Newtonienne : le problème à N corps. Les auteurs du présent ouvrage, mathématiciens spécialistes du domaine, retracent élégamment l'histoire de ce problème et de ses développements de Poincaré à nos jours.
- Forest R. Moulton ; An Introduction to Celestial Mechanics, Dover (1970) (ISBN 0-48664-687-4). Réédition de la seconde édition publiée originellement en 1914 ; un ouvrage d'introduction très clair.
Ouvrages plus techniques[modifier | modifier le code]
Les anciens[modifier | modifier le code]
- Pierre-Simon Laplace ; Traité de mécanique céleste, Éditions Jacques Gabay (1990). Réédition d'un ouvrage classique du début du XIXe siècle, en quatre volumes. Niveau second cycle universitaire[1].
- François-Félix Tisserand ; Traité de mécanique céleste, Éditions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en quatre volumes. Niveau second cycle universitaire[2].
- Henri Poincaré ; Leçons de mécanique céleste, trois tomes, (1905-1910), réédité par Jacques Gabay, Paris (2003). Une somme de référence, par le grand mathématicien qui a tant contribué au sujet. Niveau second cycle universitaire[3].
Les modernes[modifier | modifier le code]
- Vladimir I. Arnold, V.V. Kozlov & A.I. Neishtadt ; Mathematical Aspects of Classical and Celestial Mechanics, Encyclopaedia of Mathematical Sciences, Springer-Verlag (2e édition-1993).
- Vladimir I. Arnold ; Mathematical Methods of Classical Mechanics, Springer-Verlag (2e édition-1989) (ISBN 0-387-96890-3). Une synthèse de l'état de l'art en mécanique analytique (formalismes Lagrangien & Hamiltonien) avec l'accent mis sur l'interprétation géométrique de ces formalismes, par l'un des plus brillants mathématiciens du domaine. À partir du second cycle universitaire.
- Carl L. Siegel & Jürgen Moser ; Lectures on celestial mechanics, Classics in Mathematics, Springer-Verlag (1995) (ISBN 3-540-58656-3). Quelques résultats mathématiques sur le problème à trois corps. Niveau second cycle universitaire minimum.
- June Barrow-Green ; Poincaré & the three-body problem, History of Mathematics (Vol. 11), American Mathematical Society & London Mathematical Society (1997).
- Donald G. Saari ; Collisions, Rings, and Other Newtonian N-Body Problems, CBMS Regional Conference Series in Mathematics 104, American Mathematical Society (2005), (ISBN 0-8218-3250-6).
- Kenneth R. Meyer, Glen R. Hall ; Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, Applied Mathematical Sciences 90, Springer-Verlag (1991), (ISBN 0-387-97637-X).
- Vladimir I. Arnold & André Avez ; Ergodic Problems of Classical Mechanics, Advanced Book Classics, Pearson Addison Wesley () (ASIN 0201094061).
Notes et références[modifier | modifier le code]
- Traité de mécanique céleste de Pierre-Simon Laplace, sur Gallica
- Traité de mécanique céleste de François-Félix Tisserand, sur Gallica
- Leçons de mécanique céleste de Henri Poincaré, sur Gallica
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Astronomie fondamentale
- Astrophysique
- Conique
- Histoire de l'astronomie
- Lois de Kepler
- Mécanique hamiltonienne
- Mécanique newtonienne
- Mécanique spatiale
- Orbite
- Problème à deux corps
- Problème à N corps
- Système intégrable
- Système dynamique
- Théorie du chaos
- Théorie ergodique
- Théorème KAM
Liens externes[modifier | modifier le code]
- Institut de mécanique céleste et de calcul des éphémérides, Paris. (Unité mixte de recherche 8028 du CNRS)
- Les Lois de Kepler, cours en ligne de l'Observatoire de Paris
- Les Lois de Newton, cours en ligne de l'Observatoire de Paris
- Mécanique céleste cours en ligne de l'Observatoire de Paris
