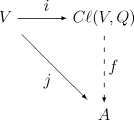Algèbre de Clifford
En mathématiques, l'algèbre de Clifford est un objet d'algèbre multilinéaire associé à une forme quadratique. C'est une algèbre associative sur un corps, permettant un type de calcul étendu, englobant les vecteurs, les scalaires et des « multivecteurs » obtenus par produits de vecteurs, et avec une règle de calcul qui traduit la géométrie de la forme quadratique sous-jacente. Le nom de cette structure est un hommage au mathématicien anglais William Kingdon Clifford.
Les algèbres de Clifford constituent l'une des généralisations possibles des nombres complexes et des quaternions. En mathématiques, elles offrent un cadre unificateur pour étudier des problèmes de géométrie tels que la théorie des formes quadratiques, et les groupes orthogonaux et introduire les spineurs et la géométrie spinorielle (en). Mais elles fournissent aussi un cadre de calcul pertinent à de nombreux domaines physiques, des plus théoriques (relativité, mécanique quantique) aux plus appliqués (vision par ordinateur, robotique). Pour ces applications, une approche simplifiée est parfois pratiquée, avec une introduction différente, limitée aux corps des réels et complexes, ce qui conduit à la structure très proche d'algèbre géométrique.
- Une certaine familiarité avec les bases de l'algèbre multilinéaire sera très utile à la lecture de cet article.
- De nombreux résultats supposent que la caractéristique du corps de base K n'est pas 2 (c'est-à-dire que la division par 2 est possible) ; on fait cette hypothèse dans toute la suite, sauf dans une section dédiée au cas particulier de la caractéristique 2.
Définition[modifier | modifier le code]
Une algèbre de Clifford est une algèbre associative unitaire associée à un espace vectoriel V muni d'une forme quadratique Q. On note < , > la forme bilinéaire symétrique associée à Q :
Introduction informelle[modifier | modifier le code]
L'algèbre de Clifford Cℓ(V,Q) est l'algèbre « la plus générale » engendrée par V, c'est-à-dire constituée de toutes les formules de sommes et produits de scalaires et vecteurs imaginables, soumises à la condition[1]
- pour tout vecteur dans
où le produit est pris à l'intérieur de l'algèbre et où est un scalaire, multiple de l'unité de l'algèbre. On peut ré-écrire cette identité fondamentale sous la forme
- pour tout
Cette idée d'algèbre « la plus générale » soumise à cette identité peut être formellement exprimée à travers la notion de propriété universelle qui suit.
Construction et propriété universelle[modifier | modifier le code]
Soient V un espace vectoriel sur un corps commutatif K, et une forme quadratique sur V. Une algèbre de Clifford Cℓ(Q) est une algèbre associative unitaire sur K munie d'une application linéaire définie par la propriété universelle suivante :
Pour toute algèbre associative A sur K munie d'une application linéaire vérifiant pour chaque vecteur de V (où 1 désigne le neutre multiplicatif de A), il existe un unique homomorphisme d'algèbres faisant commuter le diagramme suivant :
c'est-à-dire que .
En travaillant avec la forme bilinéaire symétrique associée à Q, la condition sur j est
- pour tout v w ∈ V.
Une algèbre de Clifford comme décrite ci-dessus existe toujours et peut être construite comme suit[2] : démarrer avec l'algèbre la plus générale qui contient V, concrètement l'algèbre tensorielle T(V), puis imposer l'identité fondamentale en prenant un quotient convenable. Dans notre cas, nous voulons prendre l'idéal bilatère dans engendré par tous les éléments de la forme
- pour tout
et définissons Cℓ(V,Q) comme le quotient
- .
Il est alors plus direct de montrer que Cℓ(V,Q) contient V et satisfait la propriété universelle ci-dessus, donc que Cℓ est unique à un isomorphisme près ; ainsi, on parle de l'algèbre de Clifford Cℓ(V,Q). Il suit aussi de cette construction que i est injective. Habituellement, on néglige de noter i et on considère V comme un sous-espace vectoriel de Cℓ(V,Q).
Une conséquence de la définition est que pour tous vecteurs de , l'identité est vraie dans Cℓ(V,Q). Cette propriété peut être utilisée en tant que définition alternative.
La caractérisation universelle des algèbres de Clifford montre que la construction de Cℓ(V,Q) est de nature fonctorielle. Concrètement, Cℓ peut être considéré comme un foncteur issu de la catégorie des espaces vectoriels avec formes quadratiques (dont les morphismes sont des applications linéaires préservant la forme quadratique) vers la catégorie des algèbres associatives. La propriété universelle garantit que les applications linéaires entre les espaces vectoriels (préservant la forme quadratique) s'étendent de façon unique vers les homomorphismes d'algèbres entre les algèbres de Clifford associées.
Base et dimension[modifier | modifier le code]
Si la dimension de V est n et est une base de V, alors l'ensemble
est une base de Cℓ(V,Q). Cette famille comprend un produit vide (k = 0), donc l'unité de l'algèbre. Chaque valeur de k donne éléments de la base, donc la dimension de l'algèbre de Clifford est
Il existe un ensemble de bases privilégiées pour V : les bases orthogonales. Une base orthogonale est telle que
L'identité de Clifford fondamentale implique que pour une base orthogonale
Ceci rend la manipulation des vecteurs de la base orthogonale tout à fait simple. Étant donné un produit de vecteurs distincts de la base orthogonale, on peut les placer dans un ordre standard en incluant un signe correspondant au nombre de transpositions nécessaires pour les ordonner correctement (i.e. la signature de la permutation ordonnée).
On peut aisément étendre la forme quadratique sur V vers une forme quadratique sur Cℓ(V,Q) en demandant que les éléments distincts soient orthogonaux entre eux, et en posant :
En particulier, , et la forme quadratique sur un scalaire est simplement . Ainsi, les bases orthogonales de V peuvent être étendues en une base orthogonale de Cℓ(V,Q). La forme quadratique définie de cette manière est en fait indépendante de la base orthogonale choisie (une formulation indépendante de la base sera donnée plus bas).
Exemples : les algèbres de Clifford réelles et complexes[modifier | modifier le code]
Les algèbres de Clifford les plus importantes sont celles sur les espaces vectoriels réels et complexes muni de formes quadratiques non dégénérées.
Algèbres de Clifford réelles[modifier | modifier le code]
Chaque forme quadratique non dégénérée sur un espace vectoriel réel de dimension finie est équivalente à la forme diagonale standard :
où n = p + q est la dimension de l'espace vectoriel. La paire d'entiers (p, q) est appelée la signature de la forme quadratique. L'espace vectoriel avec cette forme quadratique est souvent noté ℝp,q. L'algèbre de Clifford sur ℝp,q est notée Cℓp,q(ℝ). Le symbole Cℓn(ℝ) signifie soit Cℓn,0(ℝ), soit Cℓ0,n(ℝ), selon que les auteurs préfèrent des espaces définis positifs ou négatifs.
Une base orthonormale standard {ei} pour ℝp,q consiste en n = p + q vecteurs mutuellement orthogonaux, p ont une norme +1 et q ont une "norme" -1 (on a mis entre guillemets car à proprement parler une norme est positive). L'algèbre Cℓp,q(ℝ) aura par conséquent p vecteurs de base dont le carré sera égal à +1 et q vecteurs de base dont le carré sera égal à -1.
- Cℓ0,0(ℝ) est naturellement isomorphe à ℝ puisqu'il n'y a pas de vecteurs différents de zéro.
- Cℓ0,1(ℝ) est une algèbre à deux dimensions engendrée par un vecteur unique e1 dont le carré est égal à -1, et par conséquent est isomorphe à ℂ, le corps des nombres complexes.
- L'algèbre Cℓ0,2(ℝ) est une algèbre à quatre dimensions engendrée par {1, e1, e2, e1e2}. Les trois derniers éléments ont le carré égal à -1 et anticommutent tous, et donc, l'algèbre est isomorphe aux quaternions ℍ.
- L'algèbre suivante dans la suite, Cℓ0,3(ℝ), est une algèbre à huit dimensions isomorphe à la somme directe ℍ⊕ℍ appelée les biquaternions de Clifford.
Algèbres de Clifford complexes[modifier | modifier le code]
On peut aussi étudier les algèbres de Clifford sur les espaces vectoriels complexes. Chaque forme quadratique non dégénérée sur un espace vectoriel complexe est équivalent à la forme diagonale standard
où n = dim V, donc il existe essentiellement une seule algèbre de Clifford dans chaque dimension. Nous noterons l'algèbre de Clifford sur ℂn avec la forme quadratique standard par Cℓn(ℂ). On peut montrer que l'algèbre Cℓn(ℂ) peut être obtenue par la complexification de l'algèbre Cℓp,q(ℝ) où n = p + q :
- .
Ici Q est la forme quadratique réelle de signature (p,q), mais la complexification ne dépend pas de la signature. Les premiers cas ne sont pas difficiles à calculer. On trouve que
- (algèbre des matrices de taille 2).
Il existe une classification complète de ces algèbres : il s'avère que chacune des algèbres Cℓp,q(ℝ) et Cℓn(ℂ) est isomorphe à une algèbre de matrices sur ℝ, ℂ ou ℍ ou à la somme directe de deux algèbres de cette sorte.
Propriétés[modifier | modifier le code]
Comparaison avec l'algèbre extérieure[modifier | modifier le code]
Étant donné un espace vectoriel V, on peut construire l'algèbre extérieure , dont la définition est indépendante de toute forme quadratique sur V. Si Q = 0 alors l'algèbre de Clifford Cℓ(V,Q) n'est d'ailleurs autre que l'algèbre extérieure . Pour Q différent de zéro, il existe un isomorphisme canonique entre et Cℓ(V,Q), vus comme espaces vectoriels. Il ne respecte pas la structure d'algèbres (les lois produit), sauf dans le cas Q = 0. On peut ainsi considérer l'algèbre de Clifford Cℓ(V,Q) comme un enrichissement de l'algèbre extérieure sur V avec une multiplication qui dépend de Q.
La manière la plus facile d'établir l'isomorphisme est de choisir une base orthogonale {ei} pour V et de l'étendre en une base orthogonale pour Cℓ(V,Q) comme décrit ci-dessus. L'application est déterminée par
- .
Une telle construction demande un choix de base {ei} orthogonale, mais on peut montrer que l'isomorphisme obtenu est indépendant de ce choix.
Si la caractéristique de K est 0, on peut aussi établir l'isomorphisme par antisymétrie. Définissons les fonctions par
où la somme est prise sur le groupe symétrique sur k éléments, et où est la signature de la permutation . L'application multilinéaire fk est alternée, et induit une application linéaire . La somme directe de ces applications donne une application linéaire entre et Cℓ(V,Q), qui est un isomorphisme.
Une autre manière de voir la relation est la construction d'une filtration sur Cℓ(V,Q). Rappelons que l'algèbre tensorielle T(V) possède un filtre naturel : où Fk contient les sommes de tenseurs de rang ≤ k. Projeter ceci vers l'algèbre de Clifford donne un filtre sur Cℓ(V,Q). L'algèbre graduée associée
est naturellement isomorphe à l'algèbre extérieure .
Si est de dimension finie paire, si le corps est algébriquement clos et si la forme quadratique est non dégénérée, l'algèbre de Clifford est centrale simple. Ainsi, par le théorème d'Artin-Wedderburn, elle est (non canoniquement) isomorphe à une algèbre de matrices. Il s'ensuit que dans ce cas, possède une représentation irréductible de dimension , qui est unique à un isomorphisme (non unique) près. C'est la représentation spinorielle (en), dont les vecteurs sont appelés spineurs.
Graduation[modifier | modifier le code]
En tant qu'espace vectoriel, Cℓ(V,Q) hérite d'une ℤ-graduation de l'isomorphisme canonique avec l'algèbre extérieure . La valeur du carré d'un vecteur de V montre que la multiplication de Clifford ne respecte pas cette ℤ-graduation. Cependant il existe une graduation plus grossière, compatible avec le produit, qui consiste à regarder la parité du nombre de facteurs dans un produit de vecteurs.
On construit cette ℤ2-graduation et le morphisme associé à partir de l'application linéaire sur V. Elle conserve la forme quadratique Q et s'étend donc, par la propriété universelle des algèbres de Clifford en un automorphisme d'algèbre
- .
L'endomorphisme est une involution (i.e. son carré est l'identité), appelé involution principale ou involution de grade. L'espace Cℓ(V,Q) est somme directe des espaces propres pour -1 et 1
où . Les propriétés de vis à vis du produit se traduisent par une règle des signes
où les indices supérieurs doivent être lus modulo 2. Ainsi Cℓ(V,Q) est une algèbre ℤ2-graduée (aussi appelée superalgèbre). L'espace Cℓ 0(V,Q) forme une sous-algèbre de Cℓ(V,Q), qui est aussi une algèbre de Clifford, appelée la sous-algèbre paire. La partie Cℓ1(V,Q) appelée la partie impaire de Cℓ(V,Q) n'est pas une sous-algèbre. Cette ℤ2-graduation joue un rôle important dans l'analyse et l'application des algèbres de Clifford.
Le degré d'un élément de l'algèbre de Clifford fait référence généralement au degré dans la ℤ-graduation. Les éléments qui sont homogènes dans la ℤ2-graduation sont simplement dits pairs ou impairs.
Si V est la somme directe orthogonale d'un vecteur a non isotrope (Q(a) non nul) et d'un hyperplan U, alors Cℓ 0(V,Q) est isomorphe à Cℓ(U,-Q(a)Q), où -Q(a)Q est la forme Q restreinte à U et multipliée par -Q(a). En particulier, sur les réels, ceci implique que
- pour q > 0 et
- pour p > 0.
Dans le cas défini négatif, cela donne une inclusion qui étend la suite
De même, dans le cas complexe, on peut montrer que la sous-algèbre paire de est isomorphe à .
Plus généralement, quand l'espace V s'écrit comme somme de deux supplémentaires orthogonaux, l'algèbre de Clifford de V se calcule à partir des algèbres de Clifford de ces sous-espaces, en effectuant un produit tensoriel adapté à la ℤ2-graduation[3].
Antiautomorphismes associés[modifier | modifier le code]
En plus de l'automorphisme , il existe deux antiautomorphismes qui jouent un rôle important dans l'analyse des algèbres de Clifford. Rappelons que l'algèbre tensorielle T(V) possède un antiautomorphisme qui renverse l'ordre de tous les produits :
- .
Puisque l'idéal est invariant sous ce renversement, cette opération descend vers un antiautomorphisme de Cℓ (V,Q) appelé l'opération de transposition ou de renversement, notée par . La transposition est un antiautomorphisme : . L'opération de transposition ne fait pas usage de la ℤ2-graduation donc nous définissons un deuxième antiautomorphisme par composition de α et de la transposition. Nous appelons cette opération la conjugaison de Clifford notée :
- .
De ces deux antiautomorphismes, la transposition est la plus fondamentale[4].
Toutes ces opérations sont des involutions. On peut montrer qu'ils agissent comme ±1 sur les éléments qui sont homogènes dans la ℤ-graduation. En fait, toutes les trois opérations dépendent seulement du degré modulo 4. C’est-à-dire, si x est homogène avec un degré k, alors
- où les signes sont donnés par la table suivante :
| k mod 4 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|
| + | - | + | - | ||
| + | + | - | - | ||
| + | - | - | + |
Le produit scalaire de Clifford[modifier | modifier le code]
La forme quadratique Q sur V peut être étendue à une forme quadratique sur tout Cℓ 0(V,Q) comme expliqué plus haut (et que nous avons aussi notée par Q). Une définition de base indépendante est
où <a> désigne la partie scalaire de a (la partie de graduation 0 dans la ℤ-graduation). On peut montrer que
où les vi sont les éléments de V — cette identité n'est pas vraie pour des éléments arbitraires de Cℓ 0(V,Q).
La forme bilinéaire symétrique associée sur Cℓ 0(V,Q) est donnée par
On peut vérifier que ceci se réduit à la forme bilinéaire originale lorsqu'elle est restreinte à V. La forme bilinéaire sur tout Cℓ 0(V,Q) est non dégénérée si et seulement si elle n'est pas dégénérée sur V.
Il n'est pas difficile de vérifier que la transposition est l'adjoint de la multiplication de Clifford gauche/droite avec le respect de ce produit intérieur. C’est-à-dire,
- et
Le cas de la caractéristique 2[modifier | modifier le code]
Les formes quadratiques et les algèbres de Clifford de caractéristique 2 forment un cas exceptionnel. En particulier, si la caractéristique de K = 2, il n'est pas vrai qu'une forme quadratique est déterminée par sa forme bilinéaire symétrique, ou que chaque forme quadratique admet une base orthogonale. Il n'y a plus d'isomorphisme naturel avec l'algèbre extérieure (même s'ils restent isomorphes).
Structure des algèbres de Clifford[modifier | modifier le code]
Dans cette partie, nous supposons que l'espace vectoriel V est de dimension finie et que la forme bilinéaire de Q est non dégénérée. Une algèbre centrale simple sur K est une algèbre de matrices sur une algèbre de division (de dimension finie) avec un centre K. Par exemple, les algèbres centrales simples sur les réels sont les algèbres de matrices sur soit les réels, soit les quaternions.
- Si V possède une dimension paire, alors Cℓ(V,Q) est une algèbre centrale simple sur K.
- Si V possède une dimension paire, alors Cℓ 0(V,Q) est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes.
- Si V possède une dimension impaire, alors Cℓ(V,Q) est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes.
- Si V possède une dimension impaire, alors Cℓ 0(V,Q) est une algèbre centrale simple sur K.
La structure des algèbres de Clifford peut être établie explicitement en utilisant le résultat suivant. Supposons que U possède une dimension paire et une forme bilinéaire non singulière avec un discriminant d, et supposons que V est un autre espace vectoriel avec une forme quadratique. L'algèbre de Clifford de U+V est isomorphe au produit tensoriel des algèbres de Clifford de U et , qui est l'espace V avec sa forme quadratique multiplié par . Sur les réels, cela implique en particulier que
Ces formules peuvent être utilisées pour trouver la structure de toutes les algèbres de Clifford réelles.
Groupes liés aux algèbres de Clifford[modifier | modifier le code]
Retrouver les automorphismes orthogonaux de V[modifier | modifier le code]
Le groupe des éléments inversibles de l'algèbre de Clifford agit de façon naturelle sur l'algèbre, par automorphismes intérieurs : c'est la représentation adjointe
qui, dans le cas réel ou complexe de dimension finie, est une représentation usuelle de la théorie des groupes de Lie. Cette opération va permettre de retrouver et généraliser les groupes de transformations de la géométrie euclidienne.
Parmi les inversibles se trouvent notamment tous les vecteurs v de l'espace initial V qui sont non isotropes pour Q (). Leur image par l'application adjointe est une transformation de l'algèbre de Clifford qui laisse V stable, et qui est en fait l'opposé de la réflexion d'hyperplan orthogonal à v. Ceci explique qu'on s'intéresse également à une version tordue de la représentation adjointe :
puisque cette fois pour , on reconnaît en la réflexion d'hyperplan [5].
En vertu du théorème de Cartan-Dieudonné, si V est de dimension finie et si la forme bilinéaire de Q est non singulière, on peut, par composition, obtenir tous les éléments du groupe orthogonal de V[6].
Les groupes de la géométrie spinorielle[modifier | modifier le code]
De façon plus générale on peut chercher toutes les transformations de V induites par l'action d'éléments du groupe des inversibles. Il est nécessaire de se limiter à ceux qui laissent V stable : c'est ce que l'on appelle le groupe de Clifford. Il possède des sous-groupes ayant des propriétés intéressantes de conservation : le groupe de Clifford spécial, le groupe pinoriel ou des pineurs et groupe spinoriel ou des spineurs.
Applications[modifier | modifier le code]
Automatisation du calcul géométrique[modifier | modifier le code]
Géométrie différentielle[modifier | modifier le code]
En géométrie différentielle, on étend les constructions d'algébre extérieure dans le cadre des fibrés vectoriels. C'est le cas par exemple quand on définit définir par exemple le fibré cotangent ou plus généralement l'algèbre extérieure des formes différentielles sur une variété différentielle.
De la même façon, sur un fibré vectoriel muni d'une forme bilinéaire symétrique (tous suffisamment réguliers), on peut étendre la construction de l'algèbre de Clifford fibre par fibre et obtenir un fibré de Clifford. C'est notamment le cas sur le fibré tangent d'une variété (pseudo-)riemannienne, muni d'une métrique.
Cette construction offre d'intéressantes applications en géométrie riemannienne. Ainsi, moyennant certaines contraintes topologiques, on peut définir sur certaines variétés riemanniennes les notions de structure spinorielle ou de structure Spinc qui peuvent, en retour, éclairer les propriétés de ces variétés.
Physique[modifier | modifier le code]
Les algèbres de Clifford ont de nombreuses applications importantes en physique. Les physiciens considèrent habituellement une algèbre de Clifford comme une algèbre engendrée par des matrices appelées matrices de Dirac qui ont la propriété :
où est la matrice d'une forme quadratique de signature (p,q) – typiquement (1,3) lorsqu'on travaille dans un espace de Minkowski. Celles-ci sont exactement les relations définies pour l'algèbre de Clifford Cℓ1,3(ℂ) (à un facteur 2 sans importance près), qui par la classification des algèbres de Clifford est isomorphe à l'algèbre de matrices complexes 4 × 4. Les matrices ne sont que les matrices de la multiplication par le vecteur dans la représentation spinorielle, par rapport à une base arbitraire de spineurs.
Les matrices de Dirac furent découvertes en premier par Paul Dirac lorsqu'il essaya d'écrire une équation d'onde du premier ordre relativiste pour l'électron, et donna un isomorphisme explicite de l'algèbre de Clifford vers l'algèbre des matrices complexes. Le résultat fut utilisé pour définir l'équation de Dirac qui s'écrit très simplement dans l'algèbre de Clifford. L'algèbre de Clifford entière est utilisée dans la théorie quantique des champs.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Les mathématiciens qui travaillent avec les algèbres de Clifford réelles et préfèrent des formes quadratiques définies positives (précisément ceux travaillant dans la théorie de l'indice) utilisent quelquefois un choix de signe différent dans l'identité fondamentale de Clifford. C’est-à-dire qu'ils prennent . On peut remplacer Q par –Q en allant d'une convention à l'autre. Un exemple d'ouvrage utilisant cette autre convention est Spin Geometry de Lawson et Michelsohn, cité en référence.
- Pour toute cette section, consulter par exemple Lawson et Michelsohn 1989, p. 7-9.
- Lawson Michelsohn, p. 11.
- L'opposé est vrai lorsque la convention de signe alternative (-) pour les algèbres de Clifford est utilisée : c'est le conjugué qui est plus important. En général, les significations de la conjugaison et de la transposition sont interchangées lorsque l'on passe d'une convention de signe à une autre. Par exemple, dans la convention utilisée ici, l'inverse d'un vecteur est donné par tandis que dans la convention (-), il est donné par .
- Lawson et Michelsohn 1989, p. 12-13.
- Lawson et Michelsohn 1989, p. 17.
Références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Clifford algebra » (voir la liste des auteurs).
- (en) S. Carnahan, Borcherds Seminar Notes, Uncut, semaine 5, « Spinors and Clifford Algebras »
- (en) H. Blaine Lawson et Marie-Louise Michelsohn, Spin Geometry, PUP, (ISBN 978-0-691-08542-5)
- (en) Pertti Lounesto, Clifford Algebras and Spinors, CUP, 2001 (ISBN 978-0-521-00551-7)
- (en) Ian R. Porteous, Clifford Algebras and the Classical Groups, CUP, 1995 (ISBN 978-0-521-55177-9)
- (en) « A Swift Introduction to Geometric Algebra » [vidéo], sur youtube.com (consulté le ) (44 min 22 s)
- (en) « From Zero to Geo Introduction (Geometric Algebra Series) » [vidéo], sur youtube.com (consulté le ) (11 min 10 s)
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Algèbre de l'espace physique (en)
- Représentation des algèbres de Clifford
- Algèbre géométrique
- Paravecteur (en)
Liens externes[modifier | modifier le code]
- (en) « Clifford algebra », sur PlanetMath
- (en) Tracing the history of "Clifford algebra" (non vérifié)